4 2 Mean Value Theorem Rolles Theorem Mean

4. 2 Mean Value Theorem & Rolle’s Theorem

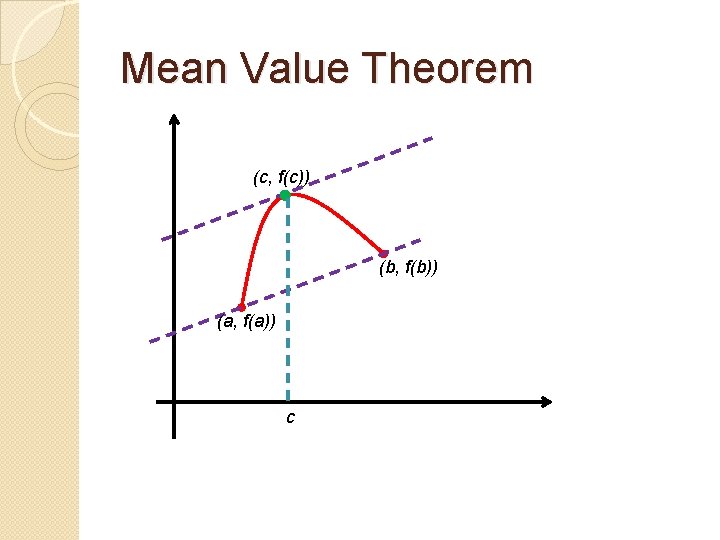
Mean Value Theorem �If f is a function that satisfies the following conditions: ◦ f is continuous on a closed interval [a, b] ◦ f is differentiable on the open interval (a, b) then there exists a number c in (a, b) such that In other words, there exists a point somewhere in (a, b) such that the instantaneous rate of change is equal to the average rate of change.

Mean Value Theorem (c, f(c)) (b, f(b)) (a, f(a)) c

Mean Value Theorem � Example: The points P(1, 1) and Q(3, 27) are on the curve f(x) = x 3. Using the Mean Value Theorem, find c in the interval (1, 3) such that f’(c) is equal to the slope of the secant of PQ. Since f(x) is defined for all real numbers, f is continuous on [1, 3]. Also, f’(x) = 3 x 2 is defined for all real numbers; thus, f’(x) is differentiable on (1, 3). Therefore, by MVT, (use only positive root since it is in the interval (1, 3))

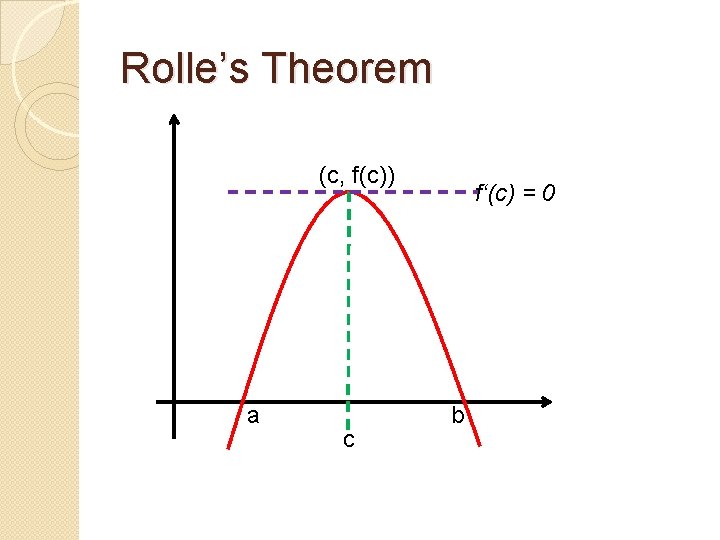
Rolle’s Theorem �If f is a function that satisfies the following three conditions: ◦ f is continuous on a closed interval [a, b] ◦ f is differentiable on the open interval (a, b) ◦ f(a) = f(b) then there exists a number c in (a, b) such that f’(c) = 0.

Rolle’s Theorem (c, f(c)) a c f‘(c) = 0 b

Rolle’s Theorem � Example: If f(x) = x 2 + 4 x – 5, show that the hypotheses of Rolle’s Theorem are satisfied on the interval [– 4, 0] and find all values of c that satisfy the conclusion of the 1. ) theorem. f(x) = x 2 + 4 x – 5 is continuous everywhere since it is a polynomial. 2. ) f’(x) = 2 x + 4 is defined for all numbers and thus is differentiable on (– 4, 0). 3. ) f(0) = f(– 4) = – 5. Therefore, there exists a c in (– 4, 0) such that f’(c) = 0 f‘(x) = 2 x + 4 = 0 x = – 2

Increasing/Decreasing Functions �A function is increasing on (x 1, x 2) if: ◦ f(x 1) < f(x 2) OR ◦ f‘(x) > 0 at each point of (x 1, x 2) �A function is decreasing on (x 1, x 2) if: ◦ f(x 1) > f(x 2) OR ◦ f‘(x) < 0 at each point of (x 1, x 2)

Antiderivatives �A function F(x) is an antiderivative of a function f(x) if F’(x) = f(x) for all x in the domain of f.