MEAN VALUE THEOREM MEAN VALUE THEOREM The expression

MEAN VALUE THEOREM

MEAN VALUE THEOREM �

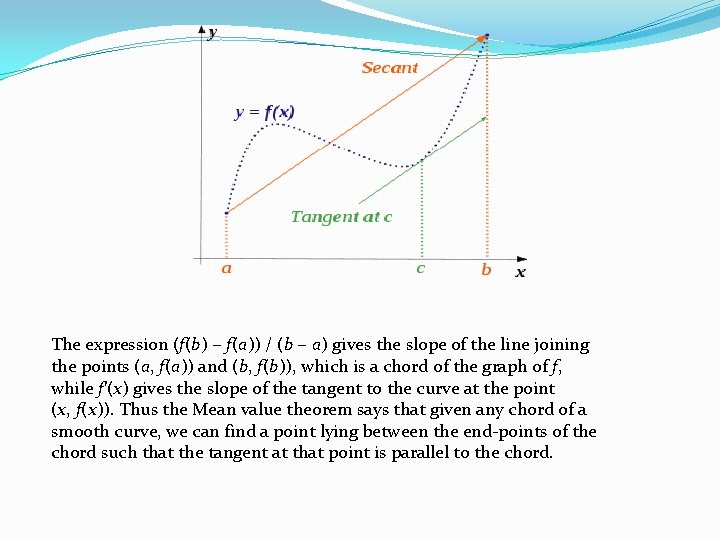
The expression (f(b) − f(a)) / (b − a) gives the slope of the line joining the points (a, f(a)) and (b, f(b)), which is a chord of the graph of f, while f′(x) gives the slope of the tangent to the curve at the point (x, f(x)). Thus the Mean value theorem says that given any chord of a smooth curve, we can find a point lying between the end-points of the chord such that the tangent at that point is parallel to the chord.

Geometrical Interpretation �

Working Rule �

Verify Lagrange’s mean value theorem for the function f(x)=(x-3)(x-6)(x-9) on the interval [3, 5]. �

Verify Lagrange’s mean value theorem for the following function on the indicated intervals. Also, find a point c in the indicated interval. F(x)=x(x-2) on [1, 3] �

Verify Lagrange’s mean value theorem for the following function on the indicated intervals. Also, find a point c in the indicated interval. f(x) = x (x-1) (x-2) on interval [0, ½] �

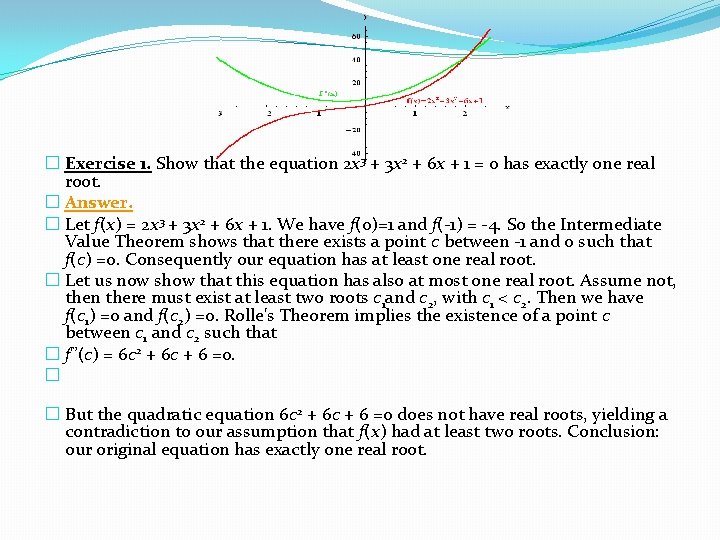
� Exercise 1. Show that the equation 2 x 3 + 3 x 2 + 6 x + 1 = 0 has exactly one real root. � Answer. � Let f(x) = 2 x 3 + 3 x 2 + 6 x + 1. We have f(0)=1 and f(-1) = -4. So the Intermediate Value Theorem shows that there exists a point c between -1 and 0 such that f(c) =0. Consequently our equation has at least one real root. � Let us now show that this equation has also at most one real root. Assume not, then there must exist at least two roots c 1 and c 2, with c 1 < c 2. Then we have f(c 1) =0 and f(c 2) =0. Rolle's Theorem implies the existence of a point c between c 1 and c 2 such that � f'’(c) = 6 c 2 + 6 c + 6 =0. � � But the quadratic equation 6 c 2 + 6 c + 6 =0 does not have real roots, yielding a contradiction to our assumption that f(x) had at least two roots. Conclusion: our original equation has exactly one real root.

Exercise �