Lecture 5 Infinite Ordinals Recall What is 2















- Slides: 16

Lecture 5 Infinite Ordinals

Recall: What is “ 2”? n Definition: 2 = {0, 1}, where 1 = {0} and 0 = {}. n n n (So 2 is a particular set of size 2. ) In general, we can define: n = {0, 1, 2, …, n 1} = {k N: k < n} This is the so-called “von Neumann” notation. We actually achieved to define the natural numbers as sets. In fact, in mathematics, everything is a set!

A Recursive Definition n Since n = {0, 1, 2, …, n 1}, n n+1 = {0, 1, 2, …, n 1, n} = {0, 1, 2, …, n 1} {n} = n {n} n Thus, we have the following recursive definition of the natural numbers: n Base: 0 = {} n Step: n+1 = n {n}

The Infinite Ordinal n For n, m N, (n m n < m) n Thus, we actually defined the order structures: n n n (n, <) = (n, ) On each n, is a transitive relation, i. e. ( i, j, k N)(i j k i k) Also, 0 1 2 3 … N Definition: = {0, 1, 2, 3, …} = N

Well Ordering n Note that (N, <) = ( , ) is linearly ordered, n i. e. ( n, m N)(n < m or n = m or m < n) n Moreover, the order (N, <) has the following nice n n feature: Every nonempty subset of N has a least element Equivalently: There is no infinite sequence x 0, x 1, x 2, x 3, … N, such that … < x 3 < x 2 < x 1 < x 0. Any linear order < with this feature is called a well order.





Ordinals versus Cardinals n Notes: n Cardinals measure sizes of sets n Ordinals measure lengths of well ordered sets n All ordinals mentioned so far, e. g. . and 0 = are actually countable sets. n There are however uncountable ordinals, 1 is the least uncountable ordinal. n In fact, 1 = the set of all countable ordinals. n Need to define what ordinals really are.

More rigorously n Definition: An ordinal is a set X such that: n X is linearly ordered by , i. e. n n ( y, z, w X)(y z and z w y w) and ( y, z X)(y z or y = z or z y) X is transitive, i. e. ( y X)(y X) Notes: From the axiom of foundation, there is no infinite sequence of sets x 1, x 2, x 3, …, such that … x 3 x 2 x 1 Thus, an ordinal is well ordered by

The Class of Ordinals n Definition: Ordinals can be classified into three classes: n The ordinal 0 n Successor ordinals = + 1 = { } n Limit ordinals = sup{ : < } = { : < } n Definitions of ordinal functions according to this classification are said to use transfinite recursion. n Proofs of ordinal statements according to this classification are said to use transfinite induction.

Ordinal Arithmetic: Addition n Definition: We define the sum of two ordinals + by recursion on : n Base ( = 0): +0= n Successor ( = + 1): + ( + 1) = ( + ) + 1 = ( + ) {( + )} n Limit ( = sup{ : < }): + = sup{ + : < } n Note: . The definition generalizes the addition of natural numbers. n Example: 1+ = < +1, so ordinal addition is not commutative, i. e. + + , in general.

Ordinal Arithmetic: Multiplication n Definition: We define the product of two ordinals n n n by recursion on : Base ( = 0): 0 = 0 Successor ( = + 1): ( + 1) = ( ) + Limit ( = sup{ : < }): + = sup{ : < } Note: . The definition also generalizes the multiplication of natural numbers. Example: 2 = < 2, so ordinal multiplication is not commutative, i. e. , in general.

Ordinal Arithmetic: Exponentiation n Definition: We define the exponentiation of two n n n ordinals by recursion on : Base ( = 0): 0 = 1 Successor ( = + 1): + 1 = Limit ( = sup{ : < }): = sup{ : < } Note: . The definition also generalizes the exponentiation of natural numbers. Example: 2 = , so ordinal exponentiation is not the same as cardinal exponentiation.

Thank you for listening. Wafik
 Infinite diversity in infinite combinations
Infinite diversity in infinite combinations 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Ramanujan infinite series
Ramanujan infinite series Sum of geometric sequence
Sum of geometric sequence Turner career and college high school
Turner career and college high school What is finite loading
What is finite loading Infinite limits and limits at infinity
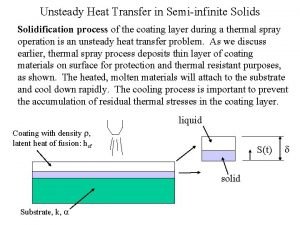
Infinite limits and limits at infinity Semi-infinite solid
Semi-infinite solid Language
Language Dvhs infinite campus
Dvhs infinite campus Energy eigenvalues of finite square well
Energy eigenvalues of finite square well Infinite computing
Infinite computing Difference between finite sequence and infinite sequence
Difference between finite sequence and infinite sequence What is a infinite set
What is a infinite set Infinite pattern definition
Infinite pattern definition What is oscillating discontinuity
What is oscillating discontinuity Complicated math
Complicated math