Konstrukcje rozkadw poprzez skadanie funkcji odwrotnych Jolanta GralaMichalak

Konstrukcje rozkładów poprzez składanie funkcji odwrotnych Jolanta Grala-Michalak Wydział Matematyki i Informatyki UAM Poznań

Ogólny opis rozważanej klasy rozkładów H: , różnowartościowa, H(0) = 0 h(x) = H’(X) > 0 dla każdego x Z = T , ( X , ) = H ( H-1 (X , ) ) Z ma jednowymiarowy rozkład ciągły = 0, - małe T(X) h(0) H-1(X) Pewsey 2009 = 0, - duże T(X/ ) H (X/h’(0)) Jones,

Johnson 1949 rozkład Su Rieck, Nedelman 1991 rozkład sinh-normalny Z N (0, 1) T (X) = sinh (X) Z = T (X) , 1 T-funkcja nieparzysta logarytmiczno-wklęsła gęstość W szczególności: 1 T (X)= arcsin h (X) dwumodalna gęstość

Rozkład sinh-arcsinh S , X , Z N(0, 1) S-1 , Z = S , (X , ) = sinh{ arcsinh(X) } X = S-1 , (Z , ) = sinh{(arcsinh(Z)+ )/ }

Gęstość rozkładu sinh-arcsinh f , (x) = (2 )-1/2 (1+x 2 )-1/2 C , (x) exp{-(1/2) S 2 , (x)} - parametr skośności < 1 „grube ogony” > 1 „lekkie ogony” F , = (S , (x)) (S , )2 + (C , )2 = 1 S , (X , ) = sinh{ arcsinh(X) } C , (X , ) = cosh{ arcsinh(Z) }

Gęstość rozkładu sinh-arcsinh = 3, = 2 = 1, = 0, 5 = 0, 2

Abe Sklar, 1959

Własności kopuł Tw. Niech C będzie kopułą. Wtedy a) C(u 2, v 2)- C(u 1, v 1 ) u 2 – u 1 + v 2 – v 1 , skąd wynika jednostajna ciągłość w dziedzinie. b) Poziomy, pionowy i diagonalny rzut kopuły w punkcie a, czyli funkcje t C(t, a), t C(a, t), t C(t, t), są niemalejące i jednostajnie ciągłe na [0, 1]. c) 0 C(u, v)/ u 1, istnieje dla prawie wszystkich u i jest niemalejąca względem v d) 0 C(u, v)/ v 1, istnieje dla prawie wszystkich v i jest niemalejąca względem u

Twierdzenie Sklara o istnieniu funkcji kopułowej, 1959

Kopuła (łac. łącznik), łączy rozkłady jednowymiarowe w dwuwymiarowy Wniosek. Kopuła jako: a) „scale invariant measure” C(u, v) = H( F-1 (u), G-1 (v) ) , gdzie F-1 (t) = inf { x : F(x) t} = sup { x : F(x) t} b) element zbioru częściowo uporządkowanego C 1 C 2 jeśli u, v [0, 1] : C 1 (u, v) C 2 (u, v) c) miara „niezależności” C = H(x, y) = F(x) G(y) x, y [- , + ]

Kopuła z 2 -wymiarowego rozkładu sinh -arcsinh-normalnego X sinh-arcsinh-norm( 1 , 1) Y sinh-arcsinh-norm( 2 , 2) Corr(X, Y) =

Kopuła z p-wymiarowego rozkładu sinh -arcsinh-normalnego = 1/2 1 = 1, 1 =2 2 = 2, 2 =1/2

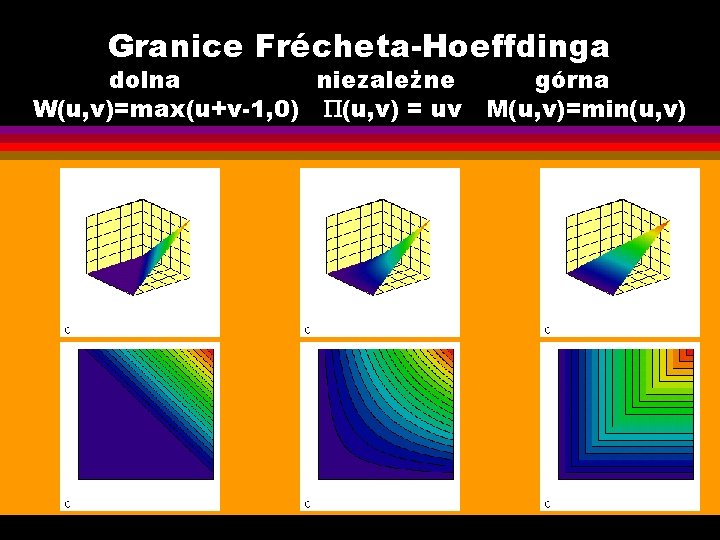
Granice Frécheta-Hoeffdinga dolna niezależne W(u, v)=max(u+v-1, 0) (u, v) = uv górna M(u, v)=min(u, v)

Metoda konstrukcji nowych wielowymiarowych dystrybuant „Meta-rozkłady” – Fang, Fang 2002 a) Wziąć znaną, 2 -wymiarową dystrybuantę H(x, y) i wyznaczyć jej dystrybuanty brzegowe F(x) i G(y) b) Znaleźć odwrotności x = F-1 (u) i y = G-1 (v) i znaleźć wzór określający kopułę C(u, v) = H( F-1 (u), G-1 (v) ) c) W miejsce u i v wstawić odwrotności innych jednowymiarowych dystrybuant F* i G* otrzymując inną, 2 -wymiarową dystrybuantę H* (x, y) = C(F* (x), G* (y))

Metoda konstrukcji nowych wielowymiarowych dystrybuant F-1 (u) = -(1/ 1 )ln(1 -u) G-1 (u) = -(1/ 2 )ln(1 -u)

Bibliografia l l l Jones, M. C. , Pewsey, A. , Sinh-arcsinh distributions, Biometrika 96 (2009), 4, pp. 761 -780. Fang, H. -B. , Fang K. -T. , The Meta-elliptical Distributions with Given Marginals, Journal of Multivariate Analysis 82 (2002), 1 -16. Landsman, Z. , Elliptical families and copulas: tilting and premium; capital allocation, Scandinavian Actuarial Journal 2 (2009), pp. 85 -103. Nelsen, R. B. , An Introduction to copulas, Springer-Verlag New York, Inc. , 1999. Bobrowski, D. , Grala, J. , Computing of Reliability Using Copulas, Safety and Reliability International Conference, vol. 2, Gdynia, 2003.