K RAVINDRA REDD Z P H S PANDYALAMADUGU

K. RAVINDRA REDD Z. P. H. S. PANDYALAMADUGU P. ADISESHAIAH Z. P. H. S. DANDIKUPPAM

INTRODUCTION S Set Theory was developed by the famous great mathematician George Canter ( 1845 -1918).

Definition of SET • Set : A set is a group of well defined objects. For representing set we use { } • A set can be represented in two ways • 1. Roster method : Elements of a set are written in between the parenthesis • 2. Set builder form : Elements of a set are described by their common property

ROSTER FORM Write the following sets in ROSTER-FORM. 1. A is the set of odd numbers bellow 20. Ans. A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}. 2. B is the set of vowels. • Ans. B = {a, e, i, o, u}. 3. P is the set of prime numbers bellow 30. Ans. P = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}. 4. F is the set of factors of 50. Ans. F = {1, 2, 5, 10, 25, 50}. 5. M is the set of multiples of 3. Ans. M = {3, 6, 9, 12, 15 …………}

SET-BUILDER FORM • Write the following sets in SET-BUILDER form. 1. A = {2, 4, 6, 8, 10, ……. . } Ans. A = {x/x is the positive even number}. 2. B = {1, 8, 27, 64, 125…. } Ans. B = { n 3 / n is positive integer}. 3. F={apple, banana, mango, orange, grapes}. Ans. F = {x / x is a fruit}. 4. W = {sun, mon, tue, wed, thu, fri, Saturday}. Ans. W = {x / x is the week day}. 5. S = {chiru, bala, naga , venki, raviteja}. Ans S = {x / x is a telugu cine film star}.

TYPES OF SETS-1 • • • SINGLETON SET A set which has only one element is called a singleton set. Ex. A = { 2 }. EMPTY SET A set which has no element in it is called an empty set. An emptyset is represented as Ǿ or { }. FINITE SET If the number of elements of a set is countable then the set is called a finite set. Ex. A = {1, 2, 3, 4, 5}. INFINITE SET If the number of elements of a set are uncountable then the set is called an infiniteset. Ex. N = {1, 2, 3, 4, 5……………. } SUBSET If every element of the set A is an element of set B then A is called subset of B. It is represented as A⊂B. Ex. A = {1, 3, 5, 7, 9} , B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} here A⊂ B. NOTE 1. Empty set is subset of every set. NOTE 2. Every set is subset of itself.

TYPES OF SETS-2 • SUPER SET If every element of set A is also an element of set B then B is called superset of A. Ex. A = {4, 8, 12, 16, 20}, B = {2, 4, 6, 8, 10. 12, 14, 16, 18, 20} here B⊃A. • PROPER SUBSET If A⊂B and A ≠ B then A is called proper subset of B. Ex. A = {1, 2, 3}, B = {1, 2, 3, 4, 5}. • IMPROPER SUBSET If A ⊂ B and A = B then A is called an improper subset of B. Ex. A={2, 4, 6}, B={2, 4, 6}. • POWER SET If A is a set, then set of all subsets of A is called powerset of A. Power set of a set A is represented as P(A). NOTE: If n(A) = n then number of elements in P(A) = 2 n

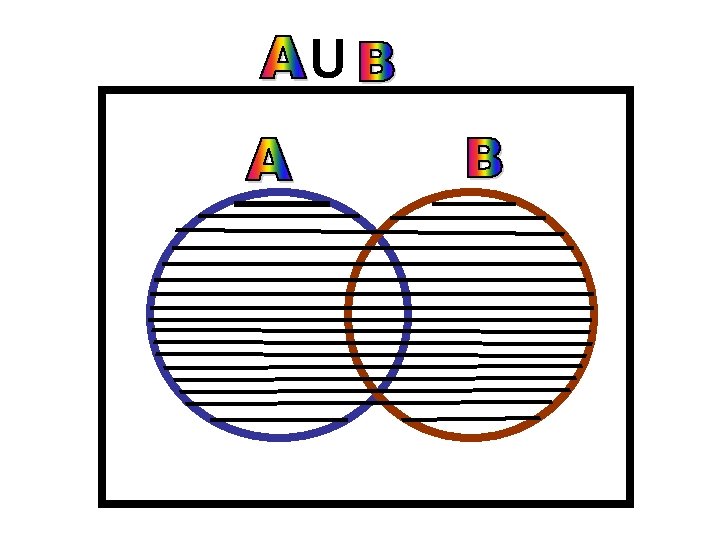
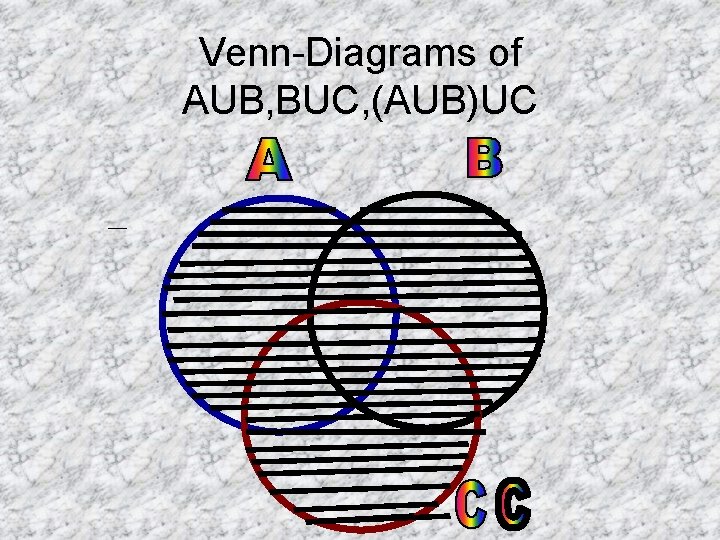
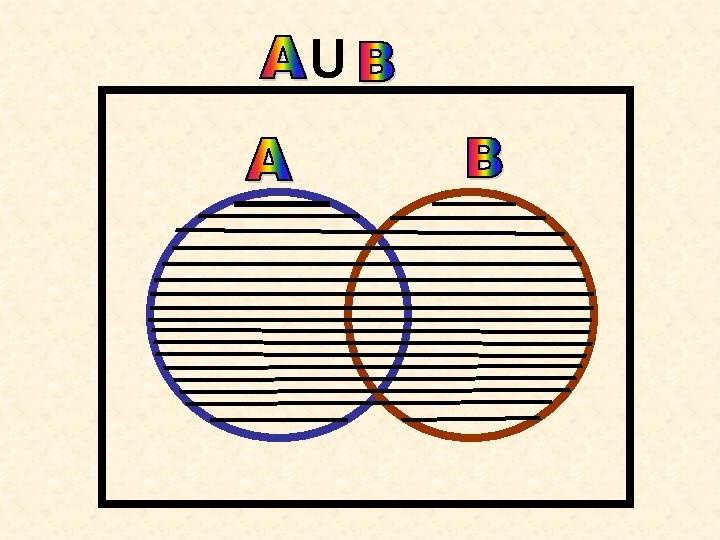
UNION OF SETS • • A={1, 2, 3} B={2, 3, 4} C={4, 5, 6} Find( AUB), (, BUC), AU(BUC), (AUB)UC AUB={1, 2, 3}U{2, 3, 4} AUB={1, 2, 3, 4, } BUA={1, 2, 3, 4} SO AUB=BUA This is called commutative law BUC={2, 3, 4, }U{4, 5, 6, } BUC={2, 3, 4, 5, 6} • AU(BUC)={1, 2, 3}U{2, 3, 4, 5, 6, } AU(BUC)={1, 2, 3, 4, 5, 6} • (AUB)UC={1, 2, 3, 4}U{4, 5, 6} (AUB)UC={1, 2, 3, 4, 5, 6} So AU(BUC)=(AUB)UC T This is called Associative law

U

Venn-Diagrams of AUB, BUC, (AUB)UC

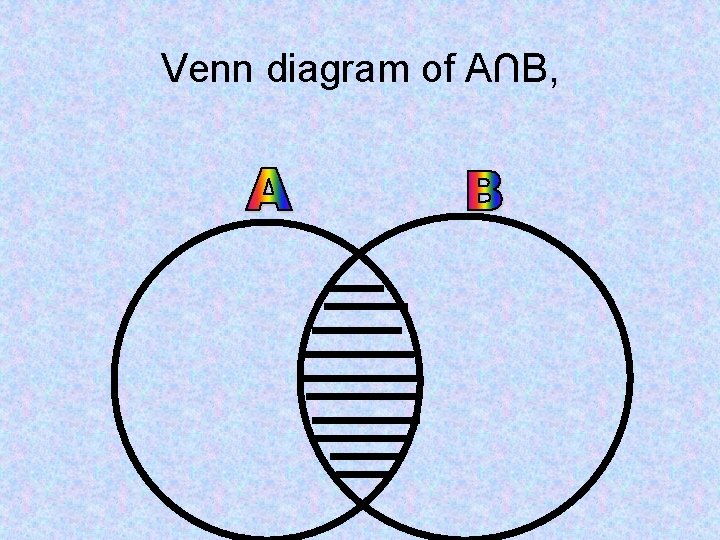
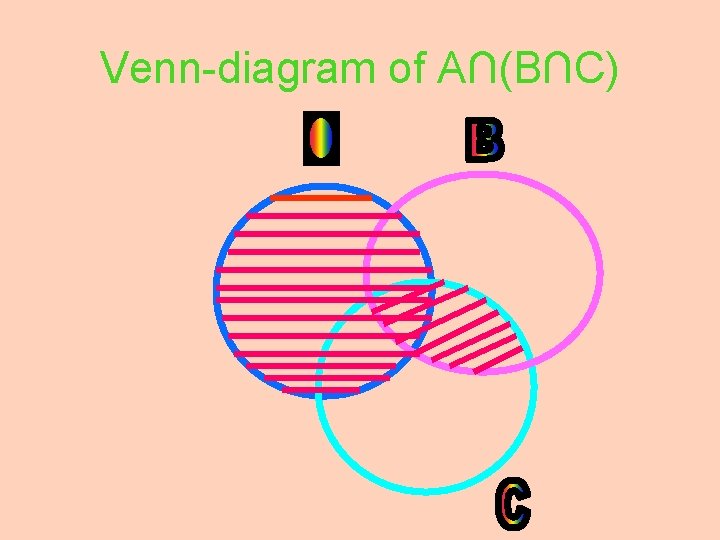
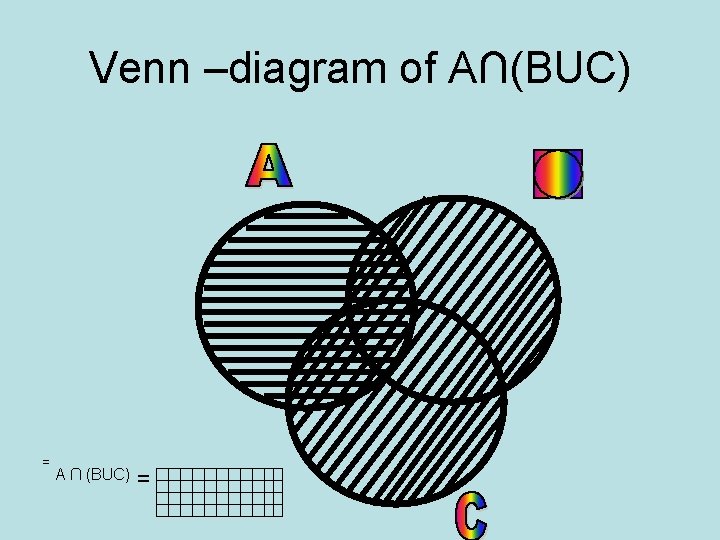
INTERSECTION OF SETS • • • • A={a, b, c, d, e} B={d, e, f} C={d, e , f, h} A∩B={a, b, c, d, e}∩{d, e, f} A∩B={d, e } B∩A={d, e, f }∩{a, b, c, d, e } B∩A={d, e} B∩C={d, e, f } ∩ {d, e, f, h } B∩C={d, e, f } C∩B={d, e, f, h} ∩ {d, e, f } C∩B={d, e, f } So Intersecton of sets following Commutative law A∩(B∩C) = {a, b, c, d, e } ∩ { d, e, f } A∩(B∩C) = {d, e } (A∩B)∩C = {, d, e } ∩ {d, e, f, h} (A∩B)∩C = {d, e }. . . A∩(B∩C) = (A∩B)∩C Intersection of SETS following Associate law

Venn diagram of A∩B,

Venn-diagram of A∩(B∩C)

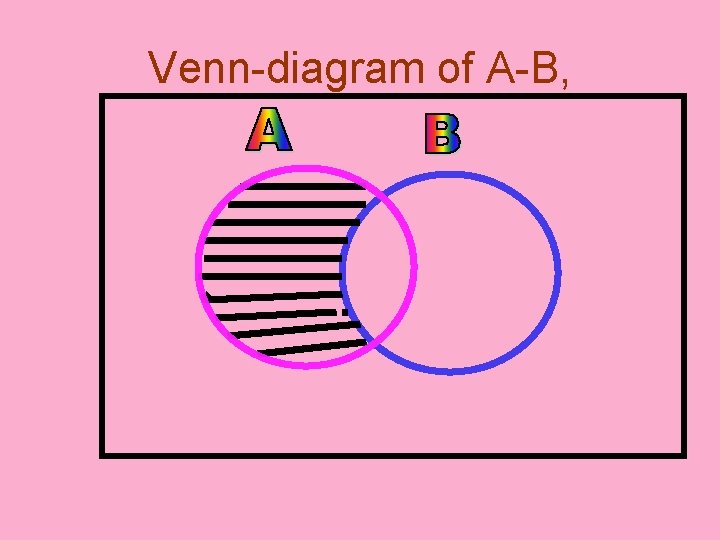
DIFFERENCE OF SETS • • A={1, 3, 5, 7, 9 }, B={1, 2, 3 } A-B={1, 3, 5, 7, 9 } – {1, 2, 3 } A-B= {5, 7, 9} B-A= {1, 2, 3 } – {1, 3, 5, 7, 9 } B-A = { 2 }. . . A-B ≠ B-A So Difference of sets not following commutative law

Venn-diagram of A-B,

SYMMETRIC DIFFERENCE OF SETS • • • • • IF A = {2, 4, 6, 8, 10 } B = { 1, 2 3, }THEN PROVE THAT A Δ B = (AUB)-(A∩B) = (A-B)U(B-A). Ans: AUB = {2, 4, 6, 8, 10 }U {1, 2, 3 } AUB = {1, 2, 3, 4, 6, 8, 10 } A∩B = {2 } (A U B ) –(A∩B ) = {1, 2, 3, 4, 6, 8, 10 } – { 2 } = {1, 3, 4, 6, 8, 10 } (A – B ) = {2, 4, 6, 8, 10 } – {1, 2, 3 } ={4, 6, 8, 10 } (B – A) = {1, 2, 3, } – { 2, 4, 6, 8, 10 } = {I, 3 } (A – B) U (B – A ) = {4, 6, 8, 10 } U { 1, 3 } = {1, 3, 4, 6, 8, 10 } So A Δ B = ( A –B ) U (B – A ) = (A U B ) – ( A ∩ B ) Here A Δ B is called Symmetri difference of sets

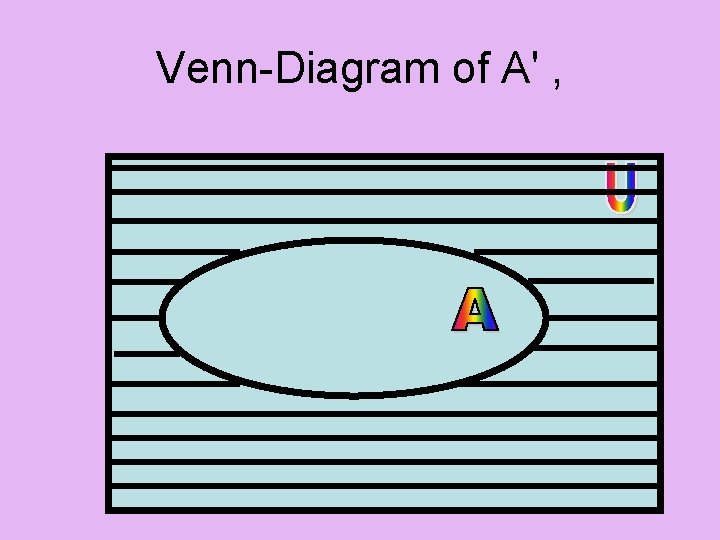
COMPLIMENT OF A SET • µ is a universal set A is any set then • (µ -A) is called Complement of A this can be represent as A' µ = {1, 2, 3, 4 ------ }, A = { 2, 4 6, --- }, B = {1, 3, 5 }, find A' , B‘ , A'∩B' , (AUB)'

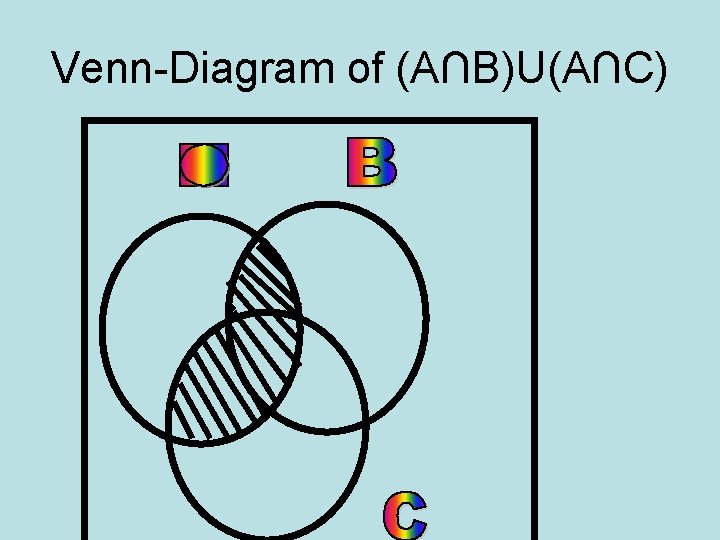
PROBLEM-1 IF A = { 1, 2, 3, 4, 5 } B = {2, 3, 4, } , C={4, 5, 6, 7} THEN PROVE THAT AU(B∩ C) = (AUB) ∩ (AUC). B∩C= {2, 3, 4} ∩ {4, 5, 6, 7 } B∩C= {4} AU(B∩C)={1, 2, 3, 4, 5 } U {4} AU(B∩C)={1, 2, 3, 4, 5 } (AUB) = {1, 2, 3, 4, 5 } U {2, 3, 4 } (AUB) ={1, 2, 3, 4, 5 } (AUC) = {1, 2, 3, 4, 5 } U {4, 5, 6, 7 } (AUC) = {1, 2, 3, 4, 5, 6, 7 } (AUB)∩(AUC) = {1, 2, 3, 4, 5, } ∩ {, 2, 3, 4, 5, 6, 7 } (AUB)∩(AUC) = {1, 2, 3, 4, 5 }. . . AU(B∩C) = (AUB) ∩ (AUC)

Venn –diagram of A∩(BUC) = A ∩ (BUC) =

Venn-Diagram of (A∩B)U(A∩C)

U

Venn-Diagram of A' ,

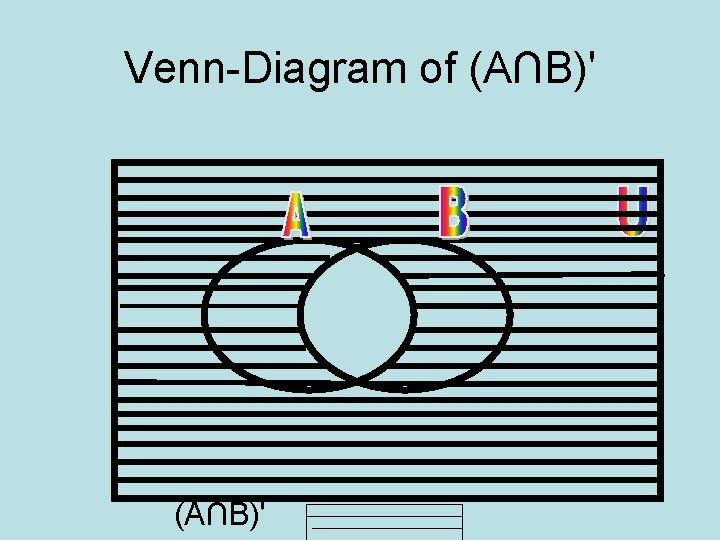
Venn-Diagram of (A∩B)'

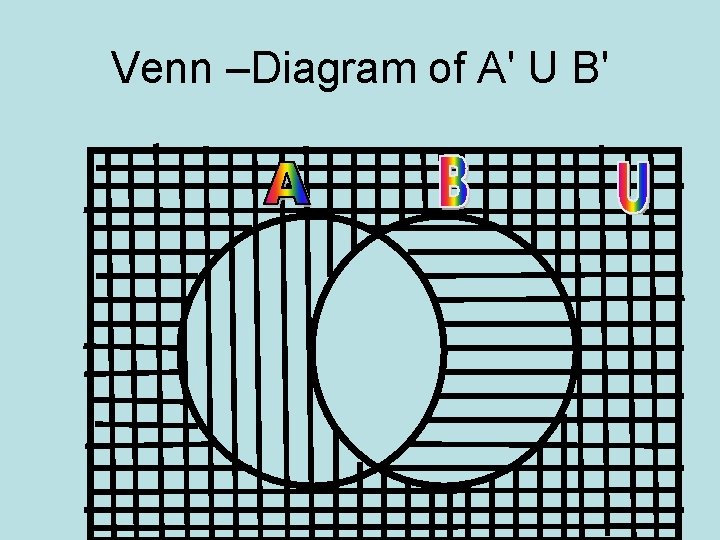
Venn –Diagram of A' U B'

Venn –Diagram of A- (

PROBLEM-4 PROBLEMS RELATING TO n(A), n(B), n(AUB) & n(A∩B). If n(AUB)= 51, n(A) = 20, n(B) =44 find n(A∩B) Ans: We know n(AUB)=n(A) +n(B)-n(A∩B) 51 = 20 + 44 – n(A∩B) = 64 -51 n(A∩B)= 13

PROBLEM-5 PROBLEMS RELATING TO n(A), n(B), n(C), n(A∩B), n(B∩C), n(C∩A) n(AUBUC) &n(A∩B∩C).

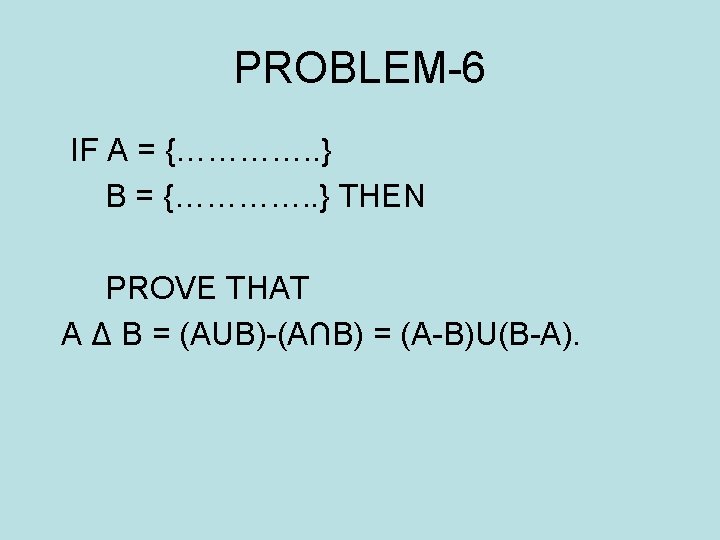
PROBLEM-6 IF A = {…………. . } B = {…………. . } THEN PROVE THAT A Δ B = (AUB)-(A∩B) = (A-B)U(B-A).

PROBLEM-7 PROVE THAT AU(B∩C) = (AUB) ∩ (AUC).

PROBLEM-8 PROVE THAT A-(BUC) = (A-B) ∩ (A-C). It is enough to prove 1. A-(BUC)⊂(A-B)∩ (A-C) 2. (A-B)∩(A-C)⊂A-(BUC)

ACKNOWLEDGEMENTS