Intermittency Crisis Whats intermittency Cause of intermittency Quantitaive

Intermittency & Crisis • • • What’s intermittency? Cause of intermittency. Quantitaive theory of intermittency. Types of intermittency & experiments. Crises Conclusions

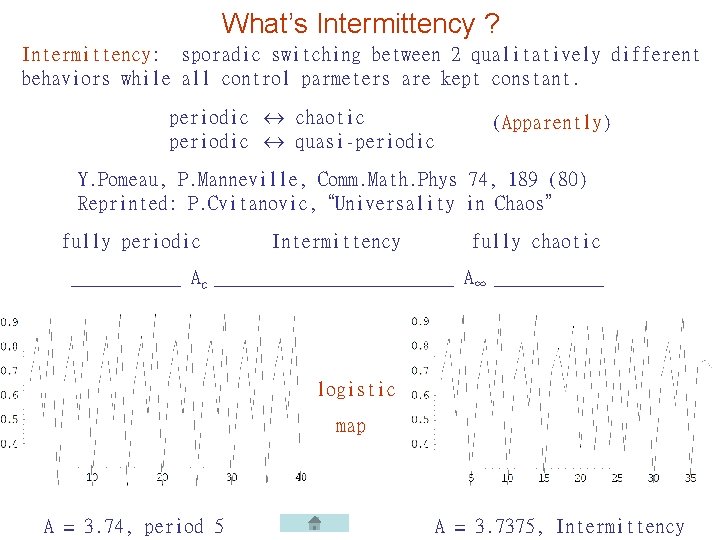
What’s Intermittency ? Intermittency: sporadic switching between 2 qualitatively different behaviors while all control parmeters are kept constant. periodic chaotic periodic quasi-periodic (Apparently) Y. Pomeau, P. Manneville, Comm. Math. Phys 74, 189 (80) Reprinted: P. Cvitanovic, “Universality in Chaos” fully periodic Intermittency fully chaotic ______ Ac ____________ A∞ ______ logistic map A = 3. 74, period 5 A = 3. 7375, Intermittency

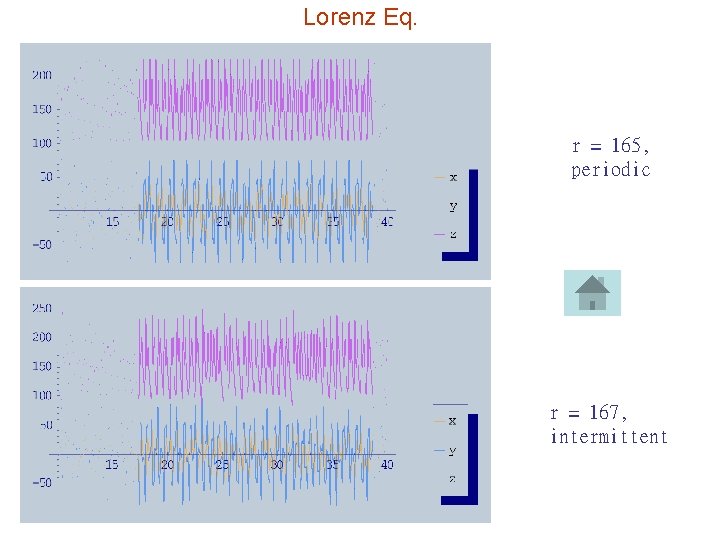
Lorenz Eq. r = 165, periodic r = 167, intermittent

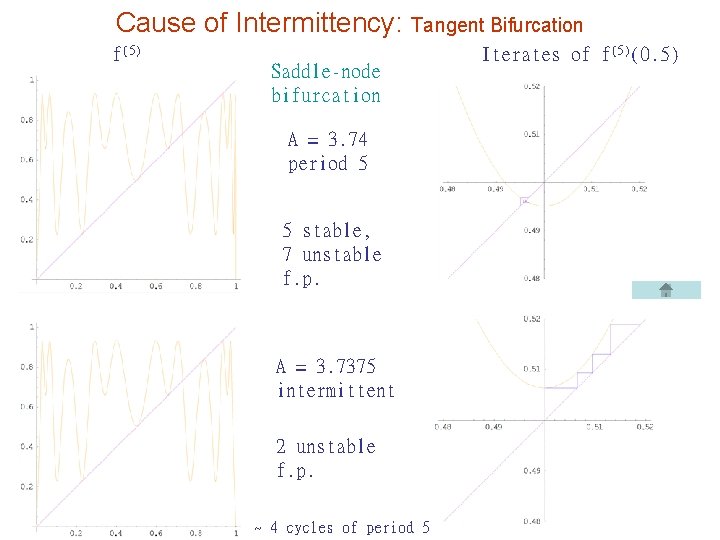
Cause of Intermittency: Tangent Bifurcation f(5) Saddle-node bifurcation A = 3. 74 period 5 5 stable, 7 unstable f. p. A = 3. 7375 intermittent 2 unstable f. p. ~ 4 cycles of period 5 Iterates of f(5)(0. 5)

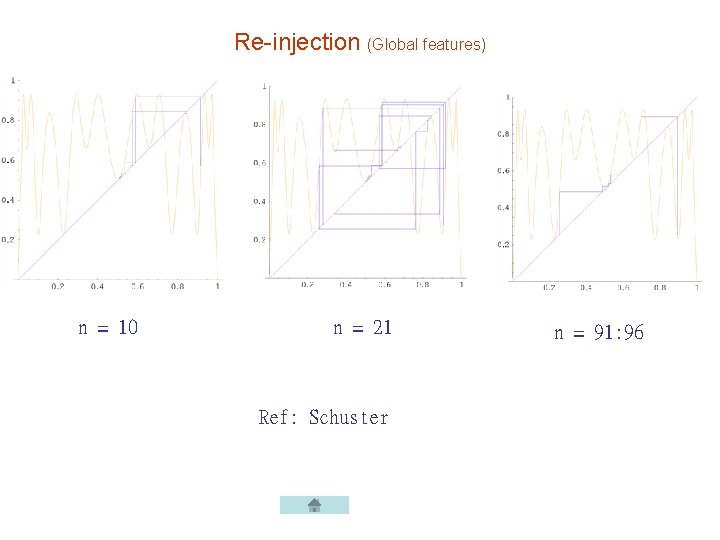
Re-injection (Global features) n = 10 n = 21 Ref: Schuster n = 91: 96

(Reverse) Tangent Bifurcation Condition for birth of tangent bifurcation at period-n window: where For A > AC, at AC for the unstable f. p. → Type I intermittency for A < AC C. f. , for period-doubling, bifurcation is at Sine-circle map, K < 1: intermittency is similar but between freq-lock & quasi-periodicity

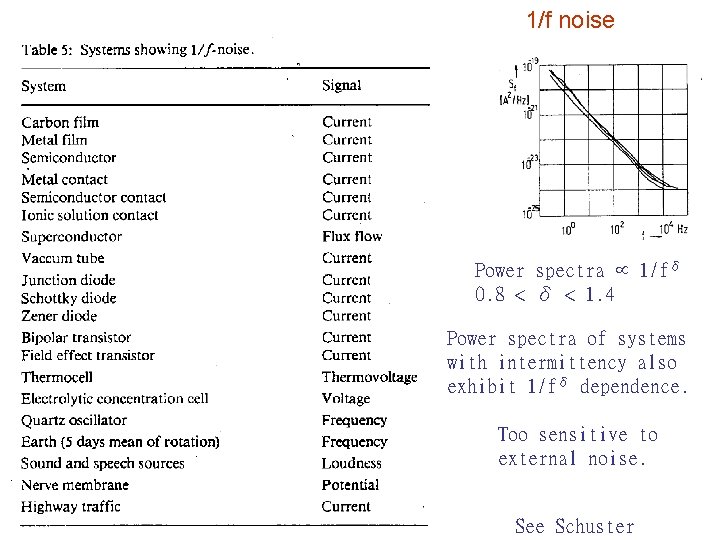
1/f noise Power spectra 1/fδ 0. 8 < δ < 1. 4 Power spectra of systems with intermittency also exhibit 1/fδ dependence. Too sensitive to external noise. See Schuster

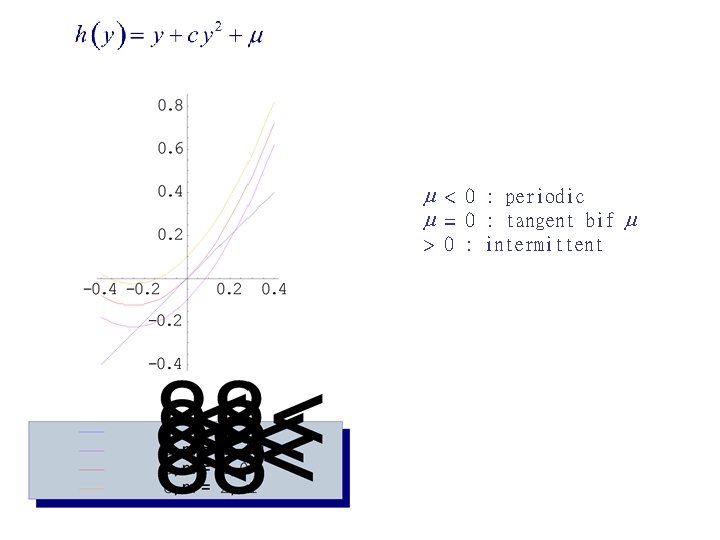
Quantitative Theory of Intermittency Tangent bifurcation near stable n-period fixed point x* ( periodic for A > AC, intermittent / chaotic for A < AC ): Set: →

< 0 : periodic = 0 : tangent bif > 0 : intermittent

Average Duration of Bursts: Renormalization Arguments L = average length of bursts of periodicity L → 0 L → ∞ for >> 1 as → 0+ < 0 : periodic = 0 : tangent bif > 0 : intermittent L n( ) = number of iterations required to pass thru gap Analogous number for h(2) is Scaling: → h(2) → h → δ = 4

h(2) → h h(2 m) → h → 4 m Ansatz: → 4 Experimental confirmation: diode circuit Renormalization theory version: with there exists g such that

Ansatz → See Schuster, p. 45 Extension to other univ classes: B. Hu, J. Rudnick, PRL 48, 1645 (82)

Types of Intermittency Type III Tangent Hopf Period- doubling xn+1 = ε+ xn + u xn 2 rn+1 = (1+ε) rn + u rn 3 xn+1 = -(1+ε) xn - u xn 3 Θn+1 = Θn + Ω ε< 0 → ε > 0 M xn On-off intermittency = Type III with new freq ~ 0

Crises Unstable fixed point / limit cycle collides with chaotic attractor → sudden changes in latter • Boundary crisis: chaotic attractor disappears • Interior crisis: chaotic attractor expands Sudden changes in fractal structure of basin boundary of chaotic attractor: metamorphosis

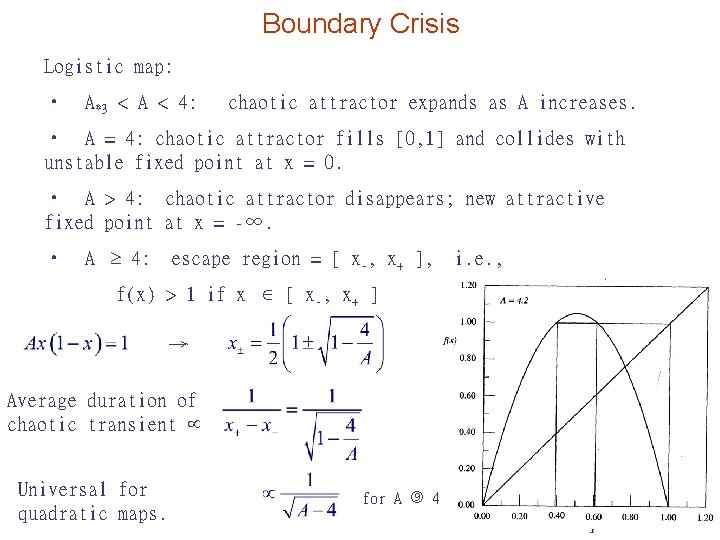
Boundary Crisis Logistic map: • A*3 < A < 4: chaotic attractor expands as A increases. • A = 4: chaotic attractor fills [0, 1] and collides with unstable fixed point at x = 0. • A > 4: chaotic attractor disappears; new attractive fixed point at x = -∞. • A 4: escape region = [ x-, x+ ], i. e. , f(x) > 1 if x [ x-, x+ ] → Average duration of chaotic transient Universal for quadratic maps. for A 4

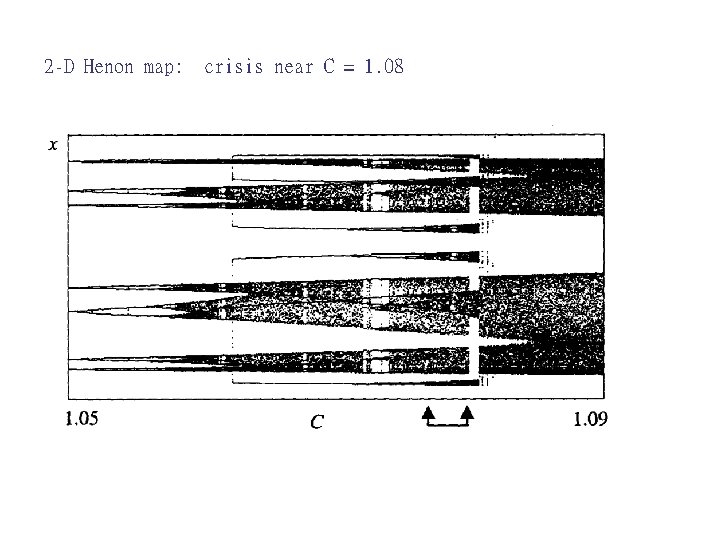
2 -D Henon map: crisis near C = 1. 08

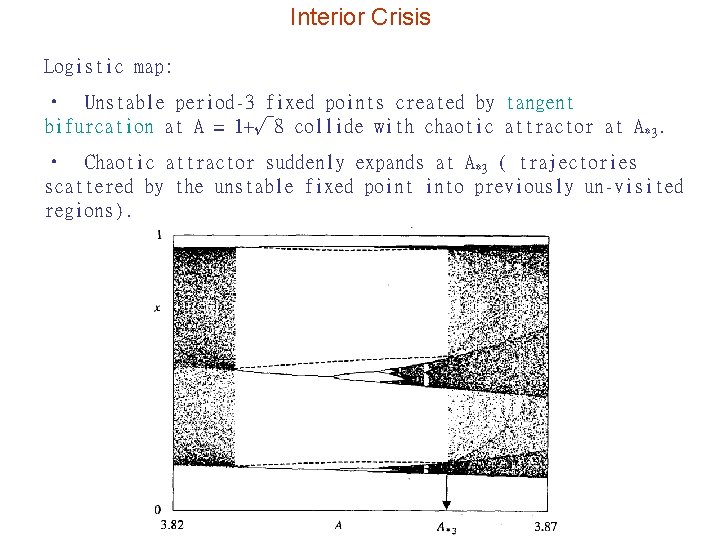
Interior Crisis Logistic map: • Unstable period-3 fixed points created by tangent bifurcation at A = 1+√ 8 collide with chaotic attractor at A*3. • Chaotic attractor suddenly expands at A*3 ( trajectories scattered by the unstable fixed point into previously un-visited regions).

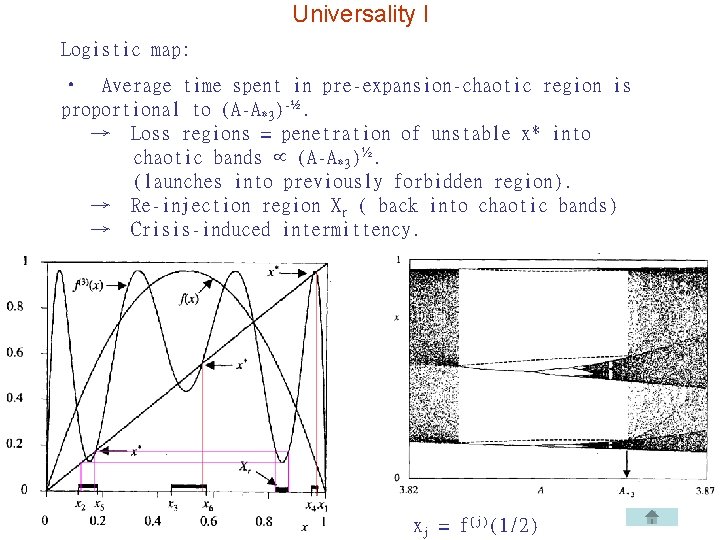
Universality I Logistic map: • Average time spent in pre-expansion-chaotic region is proportional to (A-A*3)-½. → Loss regions = penetration of unstable x* into chaotic bands (A-A*3)½. (launches into previously forbidden region). → Re-injection region Xr ( back into chaotic bands) → Crisis-induced intermittency. xj = f(j)(1/2)

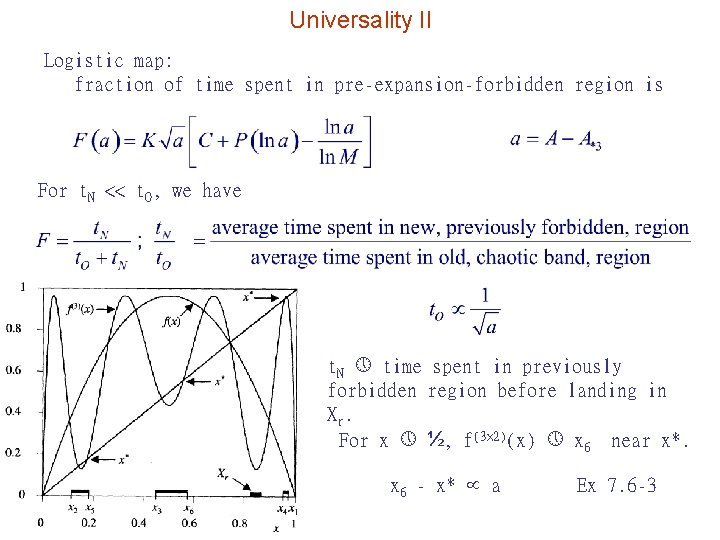
Universality II Logistic map: fraction of time spent in pre-expansion-forbidden region is For t. N << t. O, we have t. N time spent in previously forbidden region before landing in Xr. For x ½, f(3× 2)(x) x 6 near x*. x 6 - x* a Ex 7. 6 -3

Let d be the distance from x* to Xr. Let M be the Floquet multiplier for F = f(3) at x* Let → Suppose when a = an, F(n)(x) reaches Xr but not F(n-1)(x) → t. N n(an). As a increases beyond an, F(n)(x) may overshoots Xr while F(n-1)(x) hasn’t arrived → t. N becomes longer Further increase of a brings F(n-1)(x) to Xr → t. N n(an-1)-1. t. N is a periodic function of lna with period ln. M. P = some function with period ln M.

Noise–Induced Crisis Noise can bump a system in & out of crisis. Average time τ between excursions into pre-crisis gaps is described by a scaling law: where σ strength of noise Ref: J. Sommerer, et al, PRL 66, 1947 (91) Double crises H. B. Steward, et al, PRL 75, 2478 (95)