Instituto de Fsica UFRJ Transies de Fase e

Instituto de Física, UFRJ Transições de Fase e Fenômenos Críticos PG – 2º Semestre de 2007 Ementa: 1. Fenomenologia de transições de fase. 2. Modelos magnéticos simples. 3. Universalidade e scaling. 4. Métodos de aproximação. 5. Teoria de escala de tamanhos finitos. 6. Invariância conforme. 7. Sistemas desordenados. 8. Transições de fase quânticas. última atualização: 16/8/2007

Modelos magnéticos simples • • • A origem da “interação magnética” Modelo de Heisenberg isotrópico Modelo de Heisenberg anisotrópico Modelo de Ising Modelo de Heisenberg planar Modelo XY Dimensionalidade da rede magnética Simetria discreta vs. simetria contínua O modelo de Potts Universalidade: modelos de pseudo-spin

A origem da “interação magnética” “Interação magnética” responsável pelo ordenamento magnético: troca (exchange) = repulsão coulombiana + princípio de Pauli Molécula de H 2 Spins paralelos elétrons mais afastados diminui atração dos núcleos menor energia de ligação Energia (Ry) Spins anti-paralelos elétrons mais próximos aumenta atração dos núcleos maior energia de ligação Separação intermolecular (a 0) acoplamento de troca: depende do recobrimento dos orbitais atômicos

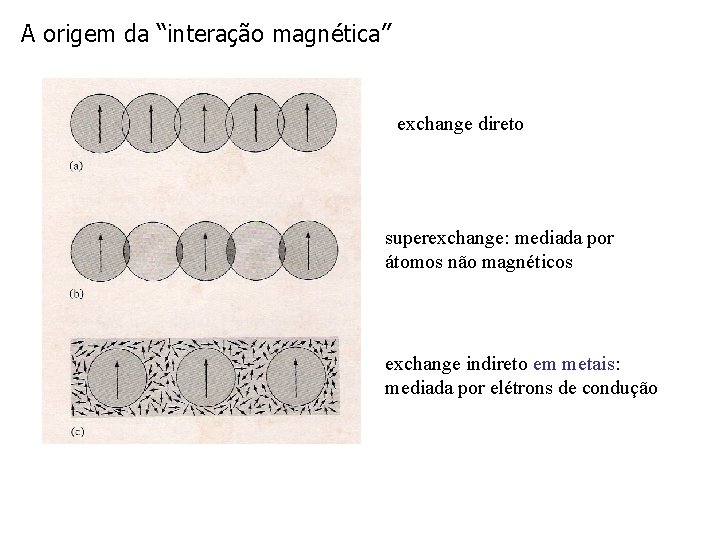
A origem da “interação magnética” exchange direto superexchange: mediada por átomos não magnéticos exchange indireto em metais: mediada por elétrons de condução

Modelo de Heisenberg isotrópico • Spins-S localizados em sítios de uma rede regular: Si magnetismo de isolantes • A interação entre pares de spin é isotrópica (no “espaço de spins”: • Alcance da interação: Jij decai com |i j| implicações para dimensionalidade efetiva da rede

Modelo de Heisenberg isotrópico • Com J > 0, o estado fundamental corresponde a ferromagnetismo saturado; • Estados excitados: ondas de spin (deslocamentos transversais compartilhados por todos os sítios) spin de cada sítio não está em um estado bem definido

Modelo de Heisenberg anisotrópico • Fontes de anisotropia de spin: campo cristalino ou campo dipolar que atuam nos momentos magnéticos Exemplo: Dy 3+ L = 5, S = 5/2, J = 15/2 • sem campo cristalino, o estado fundamental é o multipleto 2 H 15/2 degenerescência 16 • com campo cristalino uniaxial (< acoplamento spinórbita) quebra degenerescência em oito dubletes • Para Dy 3 Al 5 O 12 (DAG), Tc 2. 5 K << E/k. B ~ 80 K a baixas temperaturas o spin tem apenas dois estados, os de anisotropia máxima spin ½ efetivo • J|| ~ 100 J • melhor descrito por anisotropia single-ion 1/2 13/2 80 K 15/2

Modelo de Ising Exemplo: Co 2+ [L = 3, S = 3/2] em Co. Cs 3 Cl 5. • campo cristalino mais forte que acoplamento spin -órbita contribuição orbital para momento magnético é quenched • componente axial do campo cristalino quebra degenerescência 4 do estado fundamental • Tc 0. 52 K << E/k. B ~ 10 K a baixas temperaturas o spin tem apenas dois estados, de anisotropia máxima spin ½ efetivo • J|| ~ 10 J • melhor descrito por anisotropia Ising • Na base de autoestados de Siz , |S 1 S 2 Sn , com Si = S, (S 1), +S cada spin mantém sua individualidade pode-se substituir o operador por seu autovalor na Hamiltoniana No que diz respeito a classes de universalidade, diferença entre Heisenberg anisotrópico e Ising é imaterial; discrepâncias com relação a grandezas nãouniversais serão comentadas posteriormente.

Modelo de Heisenberg planar Exemplo: Cs. Ni. F 3. • sem exchange: campo cristalino singleto (menor energia) e dubleto • com exchange ~ gap singleto-dubleto mistura 3 estados spin efetivo S = 1 • + anisotropia single-ion favorecendo alinhamento num “plano fácil” anisotropia single-ion (só se S > ½) com D < 0: favorece o alinhamento das componentes planares

Modelo XY É o limite extremo de anisotropia planar: • spins confinados a um plano Planar XY Para grandezas universais, diferença entre planar e XY é imaterial

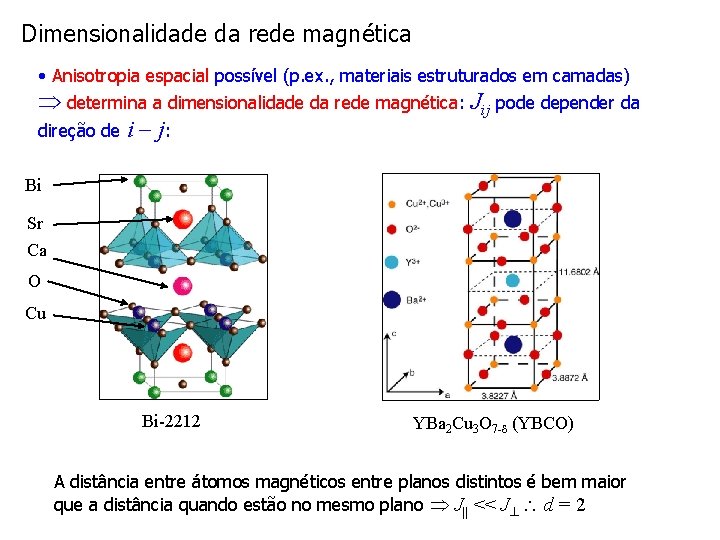
Dimensionalidade da rede magnética • Anisotropia espacial possível (p. ex. , materiais estruturados em camadas) determina a dimensionalidade da rede magnética: Jij pode depender da direção de i j: Bi Sr Ca O Cu Bi-2212 YBa 2 Cu 3 O 7 - (YBCO) A distância entre átomos magnéticos entre planos distintos é bem maior que a distância quando estão no mesmo plano J|| << J d = 2

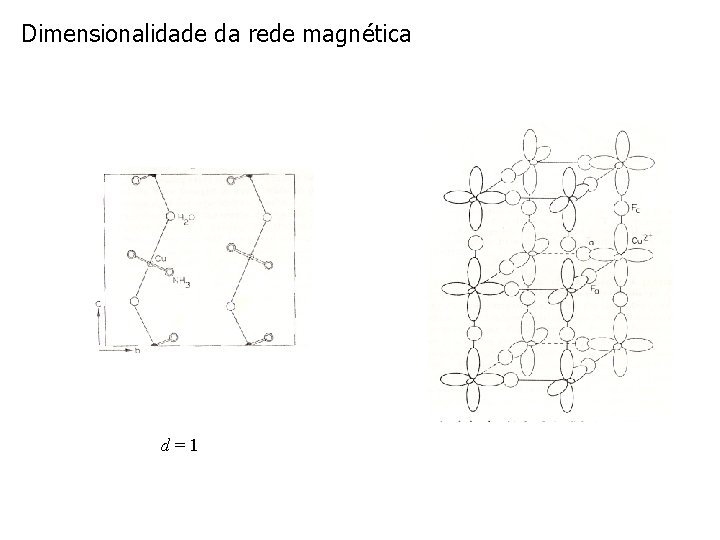
Dimensionalidade da rede magnética d=1

Simetria discreta vs. simetria contínua

Generalização do modelo de Ising: o modelo de Potts Revisão: FY Wu (1982) modelo de Ising FM: dois estados possíveis para o spin num sítio energia de interação: J se dois spins vizinhos num mesmo estado (paralelos) +J se dois spins vizinhos em estados diferentes (paralelos) N. B. : o importante é que há um E 0 separando estes estados, e não de quanto é a separação simetria discreta: {S } { S } Questão [tese de doutorado proposta por C Domb a seu estudante RB Potts (tese de doutorado, Oxford, 1951)]: como generalizar Ising para q estados, preservando a simetria discreta? Imagine vetores clássicos em cada sítio de uma rede que podem apontar em qq uma de q direções: q=2 q=3 q=4

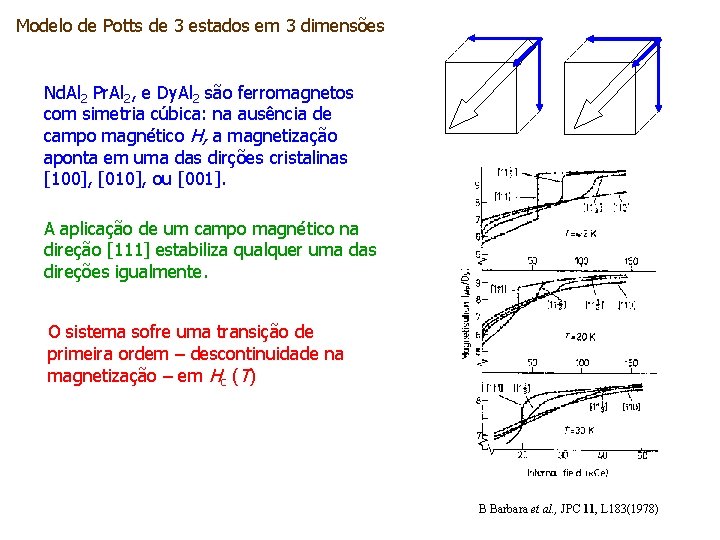
Modelo de Potts de 3 estados em 3 dimensões Nd. Al 2 Pr. Al 2, e Dy. Al 2 são ferromagnetos com simetria cúbica: na ausência de campo magnético H, a magnetização aponta em uma das dirções cristalinas [100], [010], ou [001]. A aplicação de um campo magnético na direção [111] estabiliza qualquer uma das direções igualmente. O sistema sofre uma transição de primeira ordem – descontinuidade na magnetização – em Hc (T) B Barbara et al. , JPC 11, L 183(1978)

Modelo de Potts de 3 estados em 2 dimensões Gases nobres (He, Kr, . . . ) adsorvidos na superfície de grafite; eles ocupam os centros dos hexágonos Para cobertura (i. e. , fração de sítios ocupados) 1/3, os átomos de Kr preferem ocupar uma das 3 sub-redes q = 3 Berker et al. , PRB 17, 3650 (1978)

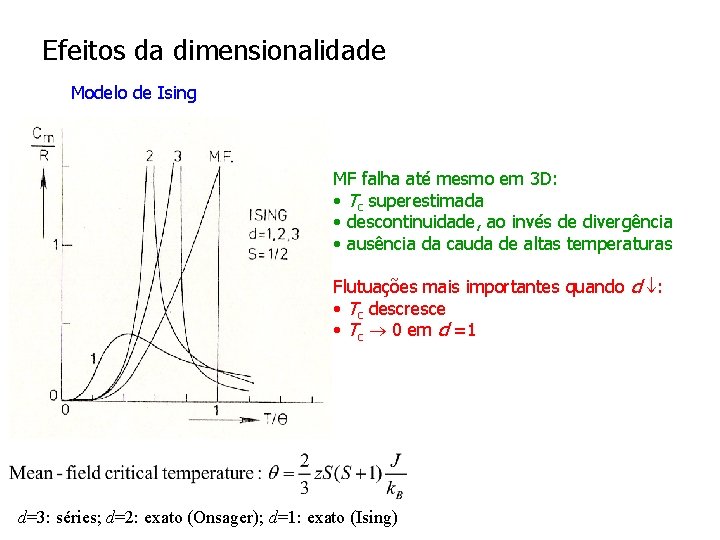
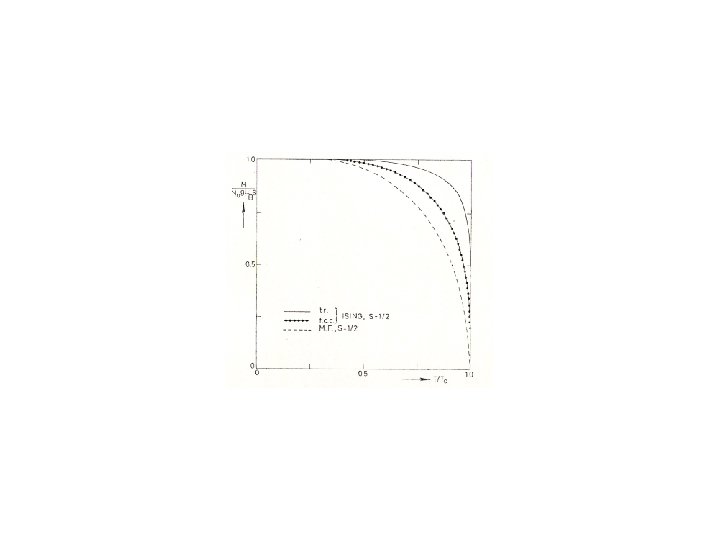
Efeitos da dimensionalidade Modelo de Ising MF falha até mesmo em 3 D: • Tc superestimada • descontinuidade, ao invés de divergência • ausência da cauda de altas temperaturas Flutuações mais importantes quando d : • Tc descresce • Tc 0 em d =1 d=3: séries; d=2: exato (Onsager); d=1: exato (Ising)

Paul Coddington, University of Adelaide, paulc@cs. adelaide. edu. au http: //www. cs. adelaide. edu. au/~paulc/physics/spinmodels. html

Referências [RMP=Rev Mod Phys; PRX=Phys Rev X; ] LJ de Jongh and AR Miedema, Adv Phys 23, 1 (1974) LP Kadanoff et al. , RMP 39, 395 (1967) HE Stanley, Introduction to Phase Transitions and Critical Phenomena, (Oxford), 1967 FY Wu, RMP 54, 235 (1982); 55, 315 (1983) (E). JM Yeomans, Statistical Mechanics of Phase Transitions, (Oxford), 1992.