Informatics Department Ionian University Informatics Department Aristotle University

Informatics Department, Ionian University Informatics Department, Aristotle University of Thessaloniki Computer Engineering and Informatics Department, Polytechnic School, University of Patras Indexing Mobile Objects on the plane Revisited S. Sioutas, K. Tsakalidis, K. Tsihlas, C. Makris & Y. Manolopoulos Data Engineering Lab The authors would like to thank the Greek. Bulgarian Bilateral Scientific Protocol for funding the above work.

Definition of Problem -Literature Survey Problem: Report the mobile objects located inside the rectangle [x 1 q , x 2 q] [y 1 q , y 2 q ] at the time instants between t 1 q and t 2 q (where tnow t 1 q t 2 q ) given the current motion information of all objects Literature Survey - Methods Geometric Duality Transformation and B+ Trees / Partition Trees TPR*-trees STRIPES 2

Problem Description Velocities are bounded by [umin, umax] Objects update their motion information, when their speed or direction changes. The system is dynamic, i. e. objects may be deleted or new objects may be inserted Let P(t 0)=[x 0, y 0] be the initial position at time t 0. Then, the object starts moving and at time t>t 0 its position will be P(t)=[x(t), y(t)]=[x 0+ux(t-t 0), y 0+uy(t-t 0)] U=[ux, uy] is its velocity vector The lines in figure below depict the objects’ trajectories on the (t, y) plane 3

Indexing Mobile Objects in one dimension Hough – X dual Transformation § It maps the line with equation y(t)=ut+a to the dual point (u, a) point in R 2 § Accordingly, the 1 -d query [(t 1 q, t 2 q), [(y 1 q, y 2 q)] becomes a polygon in the dual space (see figure above) § Thus the initial query [(t 1 q, t 2 q), [(y 1 q, y 2 q)] in (t, y) plane can be transformed to the following one query in (u. a) plane: 4

Indexing Mobile Objects in one dimension Hough – Y dual Transformation § By rewriting the equation y=ut+a as § The point in the dual plane has coordinates (b, n) where and § Thus the initial query [(t 1 q, t 2 q), [(y 1 q, y 2 q)] in (t, y) plane can be transformed to the following one query in (b, n) plane: 5

CRITERION Hough Dual Transformations ØMotions with small velocities in the Hough-Y approach are mapped into dual points (b, n) having large n coordinates (n=1/u) ØBy storing the Hough-Y dual points in an index structure such as an R* -tree, MBR's with large extents are introduced, and the performance is severely affected. ØBy using a Hough-X for the small velocities' partition, this effect is eliminated Ø The query area in Hough-X plane is enlarged by the area ØE Hough-X =E 1 hough-X + E 2 hough-X Øand in Hough-Y plane by E Hough-Y =E 1 hough-Y + E 2 hough-Y ØQ Hough-X = actual area of the simplex query in Hough-X plane ØQHough-Y = actual area of the simplex query in Hough-Y plane ØThus, the overall solution proposes the choice of that transformation which minimizes the following criterion: 6

The procedure for building the index 1. Decompose the 2 -d motion into two 1 -d motions on the (t, x) and (t, y) planes. 2. For each projection, build the corresponding index structure. Partition the objects according to their velocity: Objects with small velocity are stored using the Hough-X dual transform, while the rest are stored using the Hough-Y dual transform. Motion information about the other projection is also included. 7

Algorithm for answering the exact 2 -d query (1) Decompose the query into two 1 -d queries, for the (t, x) and (t, y) projection (2) For each projection get the dual - simplex query (3) For each projection calculate the criterion c and choose the one (say p) that minimizes it (4) Search in projection p the Hough-X or Hough-Y partition (5) Perform a refinement or filtering step ``on the fly", by using the whole motion 8 information. Thus, the result set contains

INNOVATION Q Hough-X is computed by querying a 2 -d partition tree Q Hough-Y is computed by querying a B+ tree that indexes the b parameters Our construction instead is based: (a) on the use of the Lazy B-tree [ISAAC 05] instead of the B + tree when handling queries with the Hough-Y transform and (b) on the employment of a new index that outperforms partition trees in handling polygon queries with the Hough-X transform. 9

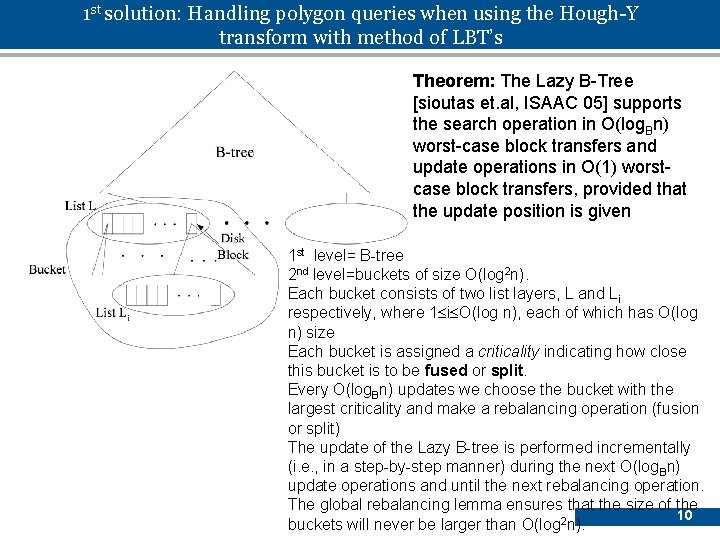
1 st solution: Handling polygon queries when using the Hough-Y transform with method of LBT’s Theorem: The Lazy B-Tree [sioutas et. al, ISAAC 05] supports the search operation in O(log. Bn) worst-case block transfers and update operations in O(1) worstcase block transfers, provided that the update position is given 1 st level= B-tree 2 nd level=buckets of size O(log 2 n). Each bucket consists of two list layers, L and Li respectively, where 1 i O(log n), each of which has O(log n) size Each bucket is assigned a criticality indicating how close this bucket is to be fused or split. Every O(log. Bn) updates we choose the bucket with the largest criticality and make a rebalancing operation (fusion or split) The update of the Lazy B-tree is performed incrementally (i. e. , in a step-by-step manner) during the next O(log. Bn) update operations and until the next rebalancing operation. The global rebalancing lemma ensures that the size of the 10 buckets will never be larger than O(log 2 n).

1 st Solution: Method of LBT’s “Two Lazy B-trees for indexing the b parameters of each dimension” Optimal Update Performance Indexing of b parameters in O(log. Bn) I/O’s in each dimension Combination of the results produced in each dimension and Filtering Indexing Performance depends on area of spatial query rectangle For sensibly realistic levels of query rectangles Very good time performance 11

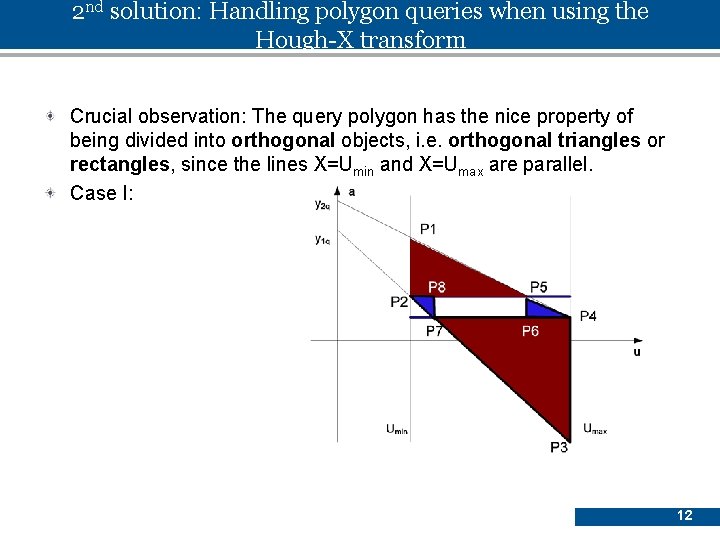
2 nd solution: Handling polygon queries when using the Hough-X transform Crucial observation: The query polygon has the nice property of being divided into orthogonal objects, i. e. orthogonal triangles or rectangles, since the lines X=Umin and X=Umax are parallel. Case I: 12

2 nd solution: Handling polygon queries when using the Hough-X transform Case III 13

2 nd solution: Handling polygon queries when using the Hough-X transform The problem of handling orthogonal range search queries has been handled in PODS 99 [Arge, Samoladas, Viter 99], where an optimal solution was presented to handle general (4 -sided) range queries in O((N/B)(log(N/B))loglog. BN) disk blocks and could answer queries in O(log. BN+T/B) I/O's, the structure also supports updates in O((log. BN)(log(N/B))/loglog. BN) I/O's. Let us now consider the problem of devising an access method for handling orthogonal triangle range queries; in this problem we have to determine all the points from a set S of n points on the plane lying inside an orthogonal triangle Let T be an orthogonal triangle defined by the point (xq, yq) and the line Lq that is not axis-parallel 14

A new 3 -layered Access Method for Triangle Range Queries (1 st layer): We sort the n points according to their xcoordinates and store the ordered sequence in a leaforiented balanced binary search tree of depth O(log n). This structure answers the query: “determine the points having xcoordinates in the range [x 1, x 2] by traversing the two paths to the leaves corresponding to x 1, x 2”. The points stored as leaves at the subtrees of the nodes which lie between the two paths are exactly these points in the range [x 1, x 2]. (2 nd layer): For each subtree, the points stored at its leaves are organized further to a second level structure according to their y-coordinates in the same way. (3 rd layer): For each subtree of the second level, the points stored at its leaves are organized further to a third level structure (Chazelle et. al [CGL 83] in main memory or Arge et. al [AAEFV 00] in external memory) for half-plane range queries. 15

Algorithm for Orthogonal Triangle Range Query 1. In the tree storing the pointset S according to x-coordinates, traverse the path to xq. All the points having x-coordinate in the range [xq, ) are stored at the subtrees on the nodes that are right sons of a node of the search path and do not belong to the path. There at most O(log n) such disjoint subtrees. 2. For every such subtree traverse the path to yq. By a similar argument as in the previous step, at most O(logn) disjoint subtrees are located, storing points that have y-coordinate in the range [yq, ). 3. For each subtree in Step 2, apply the half-plane range query of Chazelle or Arge to retrieve the points that lie on the side of line Lq towards the triangle. The correctness of the above algorithm follows from the structure used. In each of the first two steps we have to visit O(logn) subtrees. If in step 3 we apply the main memory solution of [CGL 83], then the query time becomes O(log 3 n+A), whereas the required space is O(nlog 2 n). Otherwise, if we apply the external memory solution of [AAEFV 00], then our method above requires O(log 2 nlog. Bn +A) I/O's and O(nlog 2 n) disk blocks. Although the space becomes superlinear the O(log 2 nlog. Bn +A) worst-case I/O complexity of our method is better than the O( (n/B)+A/B)) worst-case I/O complexity of a partition tree. 16

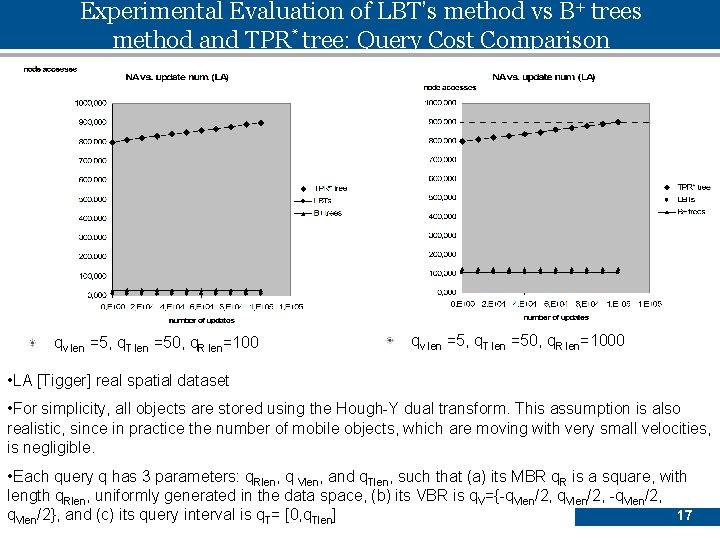
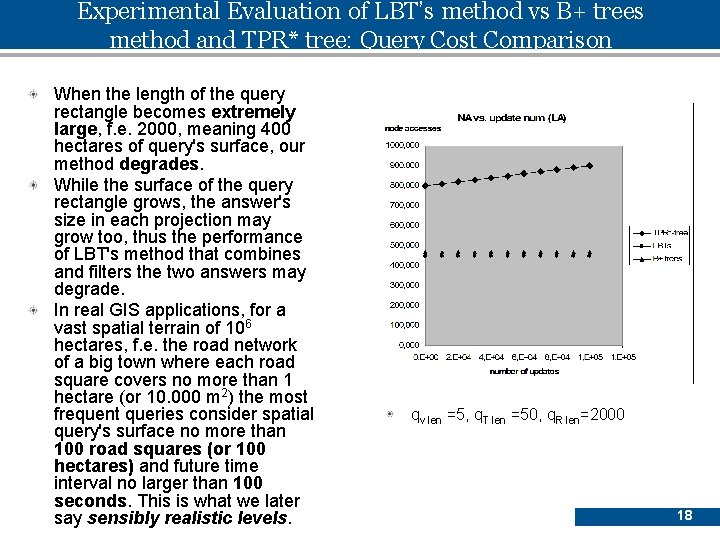
Experimental Evaluation of LBT’s method vs B+ trees method and TPR* tree: Query Cost Comparison qv len =5, q. T len =50, q. R len=1000 • LA [Tigger] real spatial dataset • For simplicity, all objects are stored using the Hough-Y dual transform. This assumption is also realistic, since in practice the number of mobile objects, which are moving with very small velocities, is negligible. • Each query q has 3 parameters: q. Rlen, q Vlen, and q. Tlen, such that (a) its MBR q. R is a square, with length q. Rlen, uniformly generated in the data space, (b) its VBR is q. V={-q. Vlen/2, 17 q. Vlen/2}, and (c) its query interval is q. T= [0, q. Tlen]

Experimental Evaluation of LBT’s method vs B+ trees method and TPR* tree: Query Cost Comparison When the length of the query rectangle becomes extremely large, f. e. 2000, meaning 400 hectares of query's surface, our method degrades. While the surface of the query rectangle grows, the answer's size in each projection may grow too, thus the performance of LBT's method that combines and filters the two answers may degrade. In real GIS applications, for a vast spatial terrain of 106 hectares, f. e. the road network of a big town where each road square covers no more than 1 hectare (or 10. 000 m 2) the most frequent queries consider spatial query's surface no more than 100 road squares (or 100 hectares) and future time interval no larger than 100 seconds. This is what we later say sensibly realistic levels. qv len =5, q. T len =50, q. R len=2000 18

Experimental Evaluation of LBT’s method vs B+ trees method and TPR* tree: Query Cost Comparison qv len =10, q. T len =50, q. R len=400 qv len =10, q. T len =50, q. R len=1000 Figures depict the efficiency of our solution in case the velocity vector grows up Obviously, the velocity factor is very important for TPR-like solutions, but it isn't for the other methods, especially this one of LBTs, which depends exclusively on query's surface factor. 19

Experimental Evaluation of LBT’s method vs B+ trees method and TPR* tree: Query Cost Comparison qv len =5, q. T len =1, q. R len=400 qv len =5, q. T len =1, q. R len=1000 Figures depict the efficiency of our solution in case the length of time interval extremely degrades to value 1 20

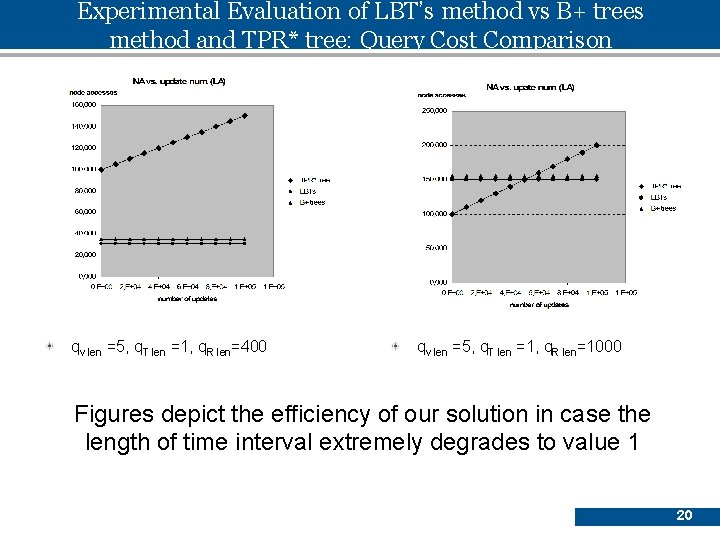
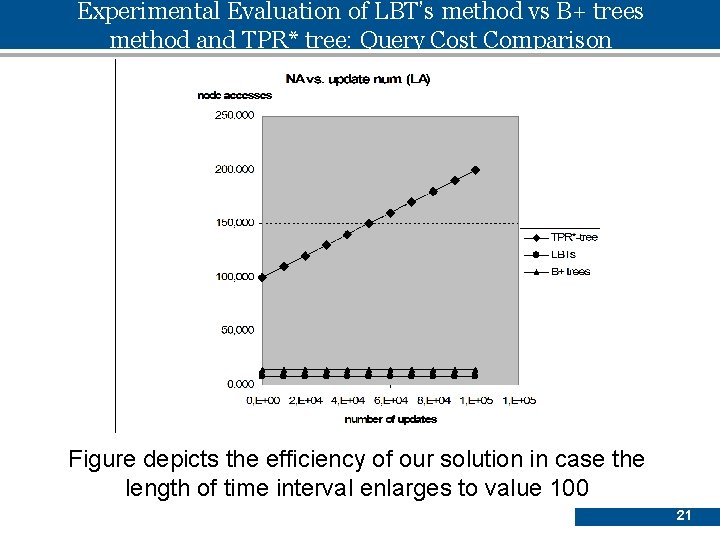
Experimental Evaluation of LBT’s method vs B+ trees method and TPR* tree: Query Cost Comparison qv len =5, q. T len =100, q. R len=400 Figure depicts the efficiency of our solution in case the length of time interval enlarges to value 100 21

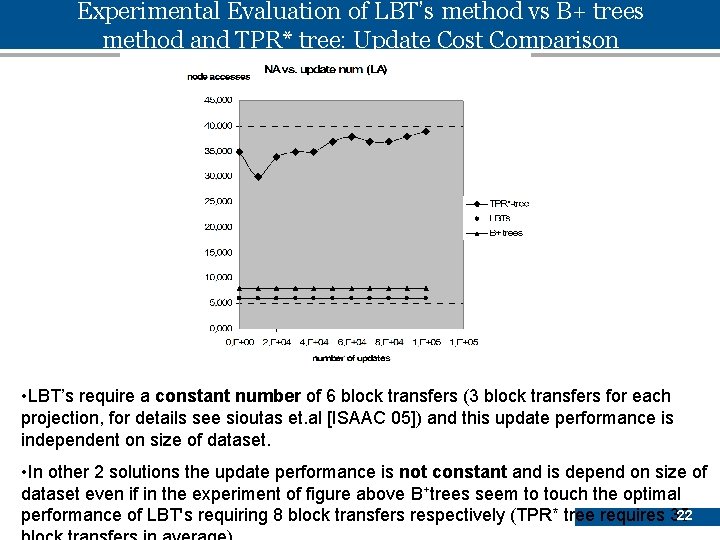
Experimental Evaluation of LBT’s method vs B+ trees method and TPR* tree: Update Cost Comparison • LBT’s require a constant number of 6 block transfers (3 block transfers for each projection, for details see sioutas et. al [ISAAC 05]) and this update performance is independent on size of dataset. • In other 2 solutions the update performance is not constant and is depend on size of dataset even if in the experiment of figure above B+trees seem to touch the optimal 22 performance of LBT's requiring 8 block transfers respectively (TPR* tree requires 35

Experimental Evaluation of LBT’s method vs B+ trees method, TPR* tree: Update Cost Comparison • According to theory, the solution of LBT's outperform the update performance of B+ trees by a logarithmic factor but this is not depicted clearly in previous Figures due to small datasets. • For this reason we performed another experiment with gigantic synthetic data sets of size n 0 [106 , 1012] (see the figure above) 23

CONCLUSIONS We presented access methods for indexing mobile objects that move on the plane to efficiently answer range queries about their location in the future Concerning the update performance evaluation our 1 st solution is the most efficient (optimal) The query performance evaluation illustrates the applicability of our 1 st solution in case the length of the query rectangle remain in sensibly realistic levels. Finally, the 2 nd very efficient solution is somehow complicated and thus it has only theoretical interest Future plan: (1) Experimental Comparison with STRIPES (it was already done in Journal Version and the results are very promising) (2) The simplification of 2 nd solution in order to be more applicable in practice. 24

Indexing Mobile Objects on the plane revisited END 25