Heaps and Priority Queues EE 312 Software Design


















- Slides: 27

Heaps and Priority Queues EE 312 Software Design and Implementation I

Full Binary Tree • Every non-leaf node has two children • All the leaves are on the same level Full Binary Tree

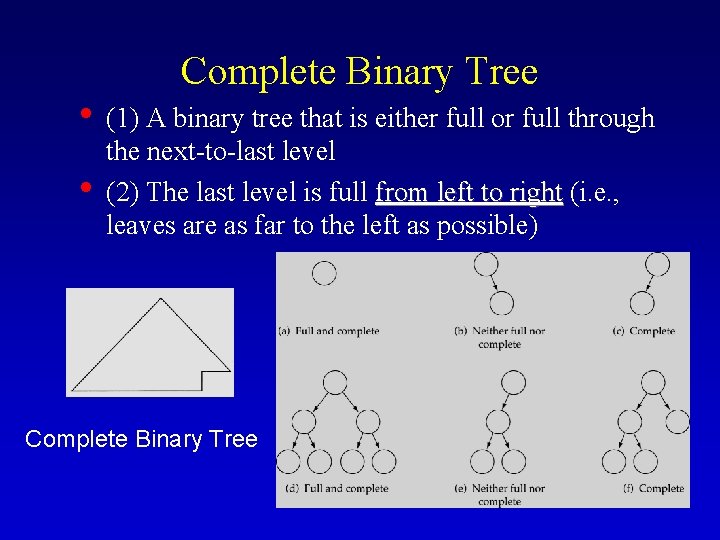
Complete Binary Tree • (1) A binary tree that is either full or full through • the next-to-last level (2) The last level is full from left to right (i. e. , leaves are as far to the left as possible) Complete Binary Tree

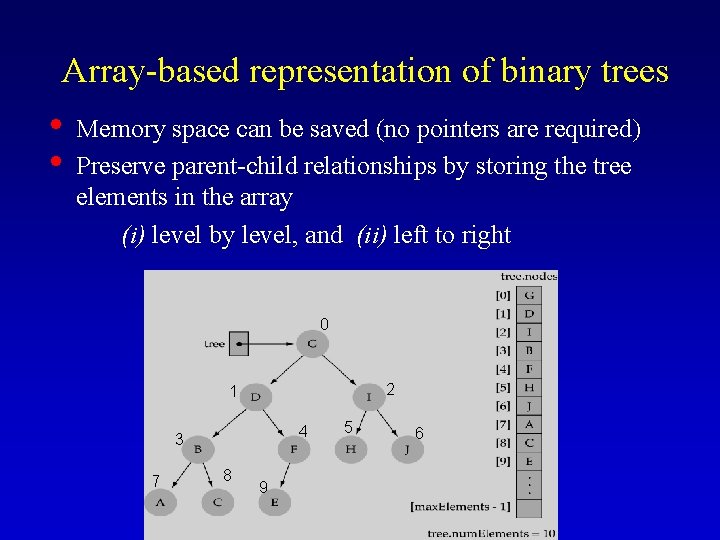
Array-based representation of binary trees • • Memory space can be saved (no pointers are required) Preserve parent-child relationships by storing the tree elements in the array (i) level by level, and (ii) left to right 0 2 1 4 3 7 8 9 5 6

Array-based representation of binary trees (cont. ) • Parent-child relationships: – left child of tree. nodes[index] = tree. nodes[2*index+1] – right child of tree. nodes[index] = tree. nodes[2*index+2] – parent node of tree. nodes[index] = tree. nodes[(index-1)/2] (int division, i. e. , truncate) • Leaf nodes: – tree. nodes[num. Elements/2] to tree. nodes[num. Elements - 1] (int division, i. e. , truncate)

Array-based representation of binary trees (cont. ) • Full or complete trees can be implemented easily using • an array-based representation (elements occupy contiguous array slots) WARNING: "Dummy nodes" are required for trees which are not full or complete

What is a heap? • It is a binary tree with the following properties: – Property 1: it is a complete binary tree – Property 2: the value stored at a node is greater or equal to the values stored at the children (heap property) property

What is a heap? (cont. ) Not unique!

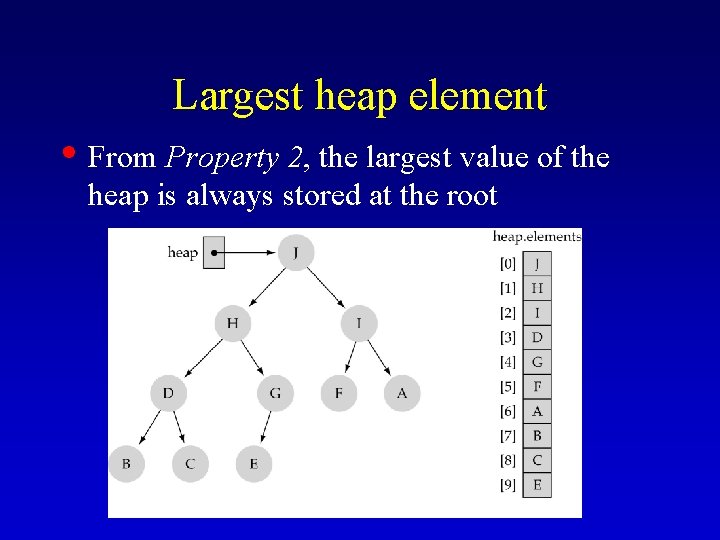
Largest heap element • From Property 2, the largest value of the heap is always stored at the root

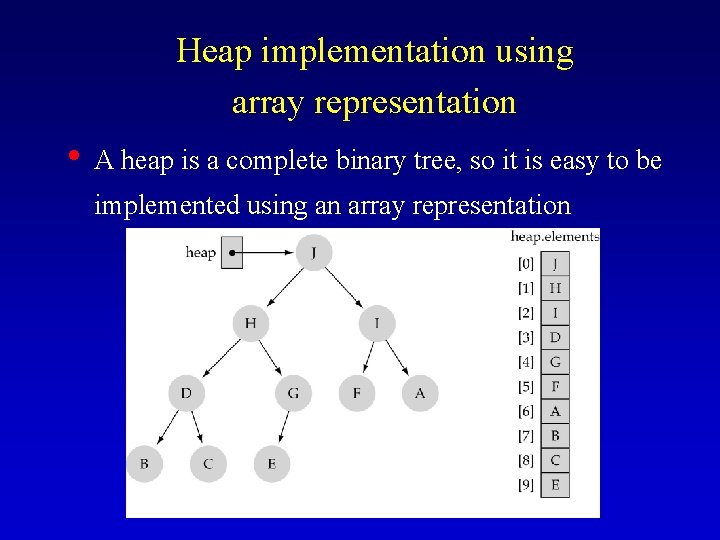
Heap implementation using array representation • A heap is a complete binary tree, so it is easy to be implemented using an array representation

Heap Specification template<class Item. Type> struct Heap. Type { void Reheap. Down(int, int); void Reheap. Up(int, int); Item. Type *elements; int num. Elements; // heap elements };

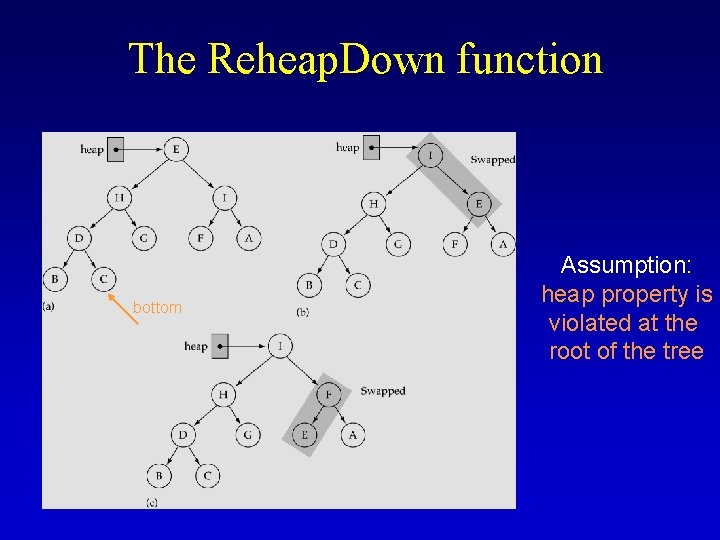
The Reheap. Down function bottom Assumption: heap property is violated at the root of the tree

Reheap. Down function template<class Item. Type> void Heap. Type<Item. Type>: : Reheap. Down(int root, int bottom) { int max. Child, right. Child, left. Child; left. Child = 2*root+1; right. Child = 2*root+2; if(left. Child <= bottom) { // left child is part of the heap if(left. Child == bottom) // only one child max. Child = left. Child; else { if(elements[left. Child] <= elements[right. Child]) max. Child = right. Child; else max. Child = left. Child; } if(elements[root] < elements[max. Child]) { Swap(elements, root, max. Child); Reheap. Down(max. Child, bottom); } } } rightmost node in the last level

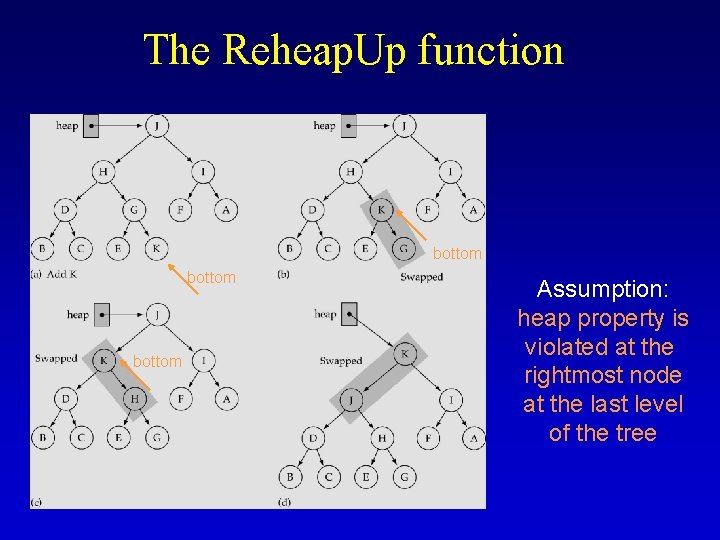
The Reheap. Up function bottom Assumption: heap property is violated at the rightmost node at the last level of the tree

Reheap. Up function Assumption: heap property is violated at bottom template<class Item. Type> void Heap. Type<Item. Type>: : Reheap. Up(int root, int bottom) { int parent; if(bottom > root) { // tree is not empty parent = (bottom-1)/2; if(elements[parent] < elements[bottom]) { Swap(elements, parent, bottom); Reheap. Up(root, parent); } } }

Priority Queues • What is a priority queue? – It is a queue with each element being associated with a "priority" – From the elements in the queue, the one with the highest priority is dequeued first

Priority queue specification template<class Item. Type> class PQType { public: PQType(int); ~PQType(); void Make. Empty(); bool Is. Empty() const; bool Is. Full() const; void Enqueue(Item. Type); void Dequeue(Item. Type&); private: int num. Items; // num of elements in the queue Heap. Type<Item. Type> heap; int max. Items; // array size };

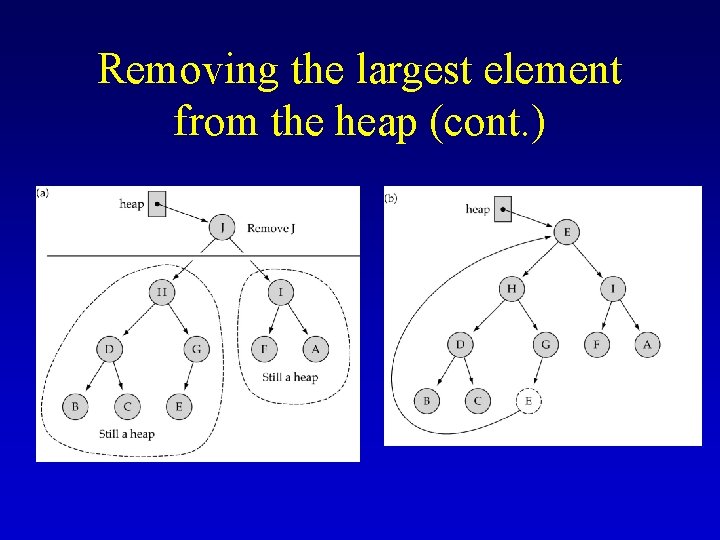
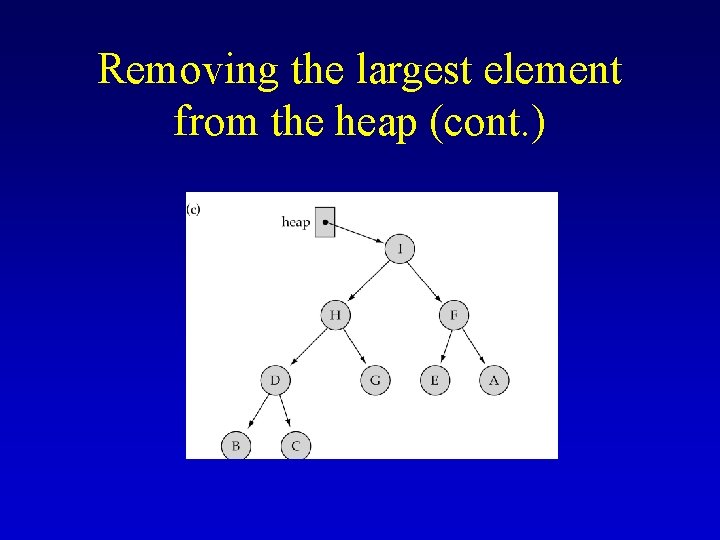
Dequeue: remove the largest element from the heap (1) Copy the bottom rightmost element to the root (2) Delete the bottom rightmost node (3) Fix the heap property by calling Reheap. Down

Removing the largest element from the heap (cont. )

Removing the largest element from the heap (cont. )

Dequeue template<class Item. Type> void PQType<Item. Type>: : Dequeue(Item. Type& item) { item = heap. elements[0]; heap. elements[0] = heap. elements[num. Items-1]; num. Items--; heap. Reheap. Down(0, num. Items-1); bottom }

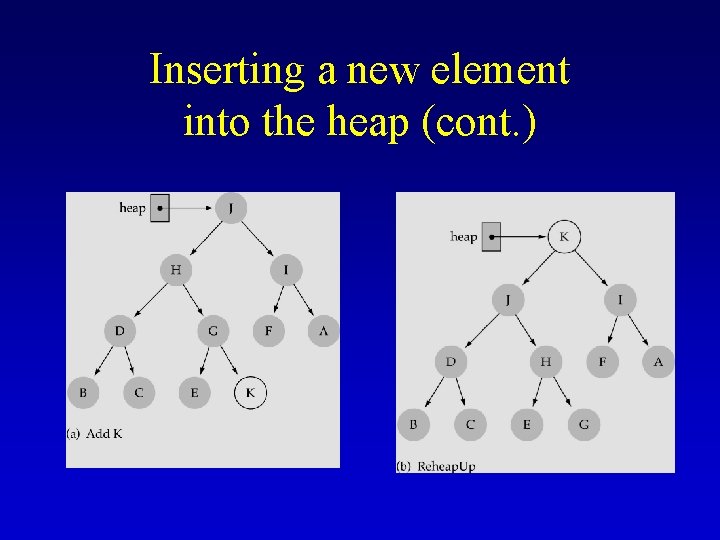
Enqueue: insert a new element into the heap (1) Insert the new element in the next bottom leftmost place (2) Fix the heap property by calling Reheap. Up

Inserting a new element into the heap (cont. )

Enqueue template<class Item. Type> void PQType<Item. Type>: : Enqueue(Item. Type new. Item) { num. Items++; heap. elements[num. Items-1] = new. Item; heap. Reheap. Up(0, num. Items-1]); } bottom

Other Functions template<class Item. Type> PQType<Item. Type>: : PQType(int max) { max. Items = max; heap. elements = new Item. Type[max]; num. Items = 0; } template<class Item. Type> PQType<Item. Type>: : Make. Empty() { num. Items = 0; } template<class Item. Type> PQType<Item. Type>: : ~PQType() { delete [] heap. elements; }

Other Functions (cont. ) template<class Item. Type> bool PQType<Item. Type>: : Is. Full() const { return num. Items == max. Items; } template<class Item. Type> bool PQType<Item. Type>: : Is. Empty() const { return num. Items == 0; }

Comparing heaps with other priority queue implementations • Priority queue using a sorted list 12 4 O(N) on the average! • Priority queue using heaps - Remove a key in O(log. N) time - Insert a key in O(log. N) time O(lg. N) on the average!