Heaps and the Heapsort Heaps and priority queues

Heaps and the Heapsort Heaps and priority queues Heap structure property Heap ordering property Removal of top priority node Inserting a new node into the heap The heap sort

Heaps and priority queues A heap is a data structure used to implement an efficient priority queue. The idea is to make it efficient to extract the element with the highest priority the next item in the queue to be processed. We could use a sorted linked list, with O(1) operations to remove the highest priority node and O(N) to insert a node. Using a tree structure will involve both operations being O(log 2 N) which is faster.

Heap structure and position numbering 1 A heap can be visualised as a binary tree in which every layer is filled from the left. For every layer to be full, the tree would have to have a size exactly equal to 2 n 1, e. g. a value for size in the series 1, 3, 7, 15, 31, 63, 127, 255 etc. So to be practical enough to allow for any particular size, a heap has every layer filled except for the bottom layer which is filled from the left.

Binary Heap Properties 1. Structure Property 2. Ordering Property 4

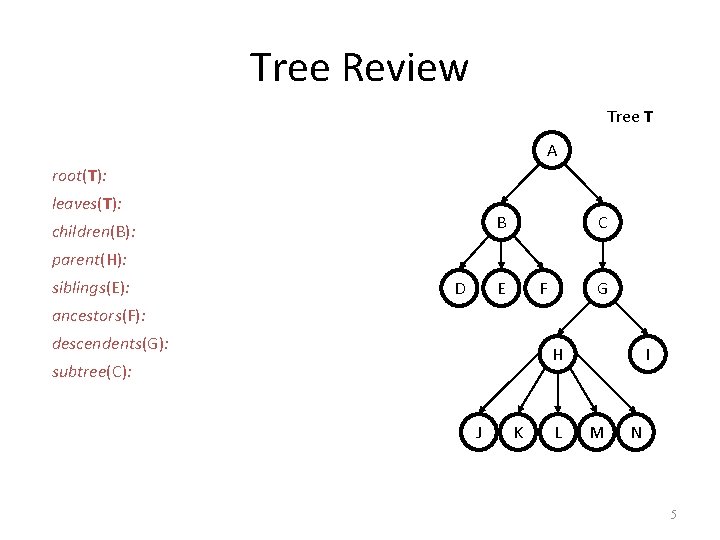
Tree Review Tree T A root(T): leaves(T): B children(B): C parent(H): siblings(E): D E F G ancestors(F): descendents(G): H subtree(C): J K L I M N 5

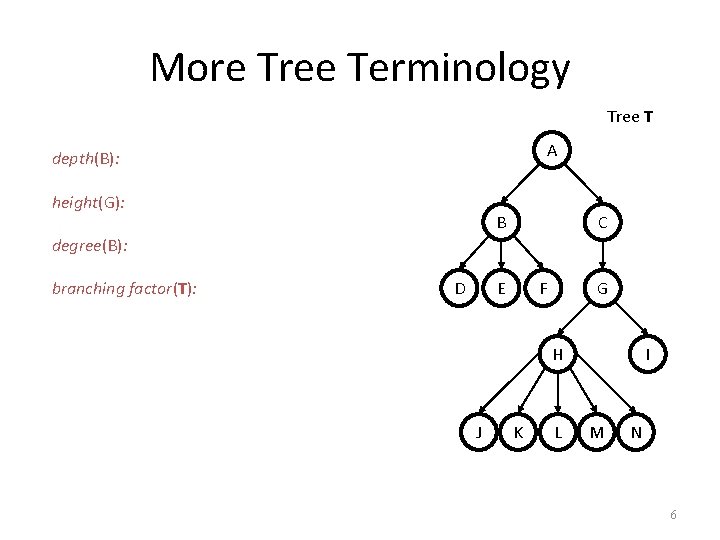
More Tree Terminology Tree T A depth(B): height(G): B C degree(B): branching factor(T): D E F G H J K L I M N 6

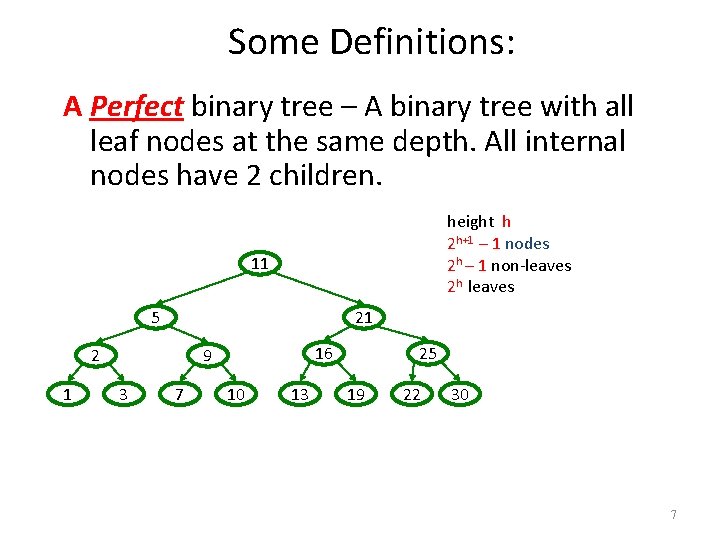
Some Definitions: A Perfect binary tree – A binary tree with all leaf nodes at the same depth. All internal nodes have 2 children. height h 2 h+1 – 1 nodes 2 h – 1 non-leaves 2 h leaves 11 5 21 2 1 16 9 3 7 10 13 25 19 22 30 7

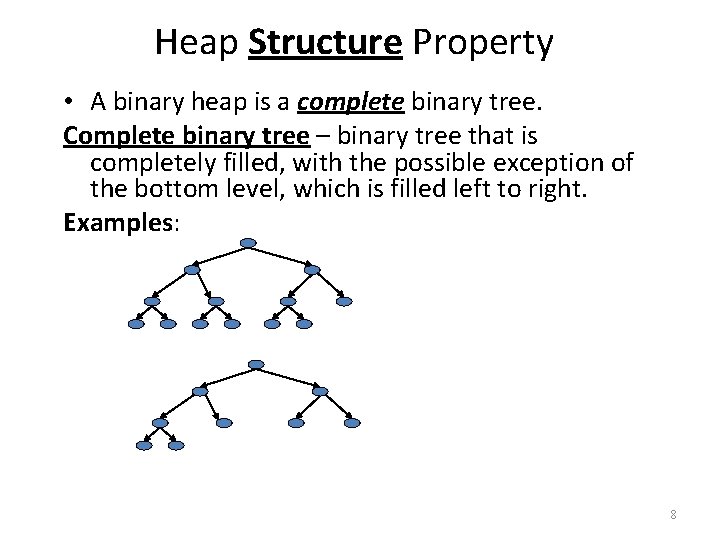
Heap Structure Property • A binary heap is a complete binary tree. Complete binary tree – binary tree that is completely filled, with the possible exception of the bottom level, which is filled left to right. Examples: 8

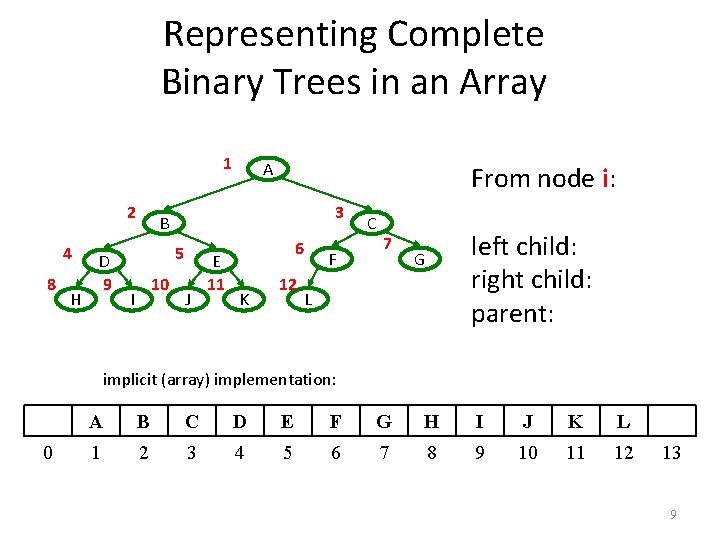
Representing Complete Binary Trees in an Array 1 2 4 8 H D 9 A From node i: 3 B 5 10 I J E 11 6 K 12 F C 7 left child: right child: parent: G L implicit (array) implementation: 0 A B C D E F G H I J K L 1 2 3 4 5 6 7 8 9 10 11 12 13 9

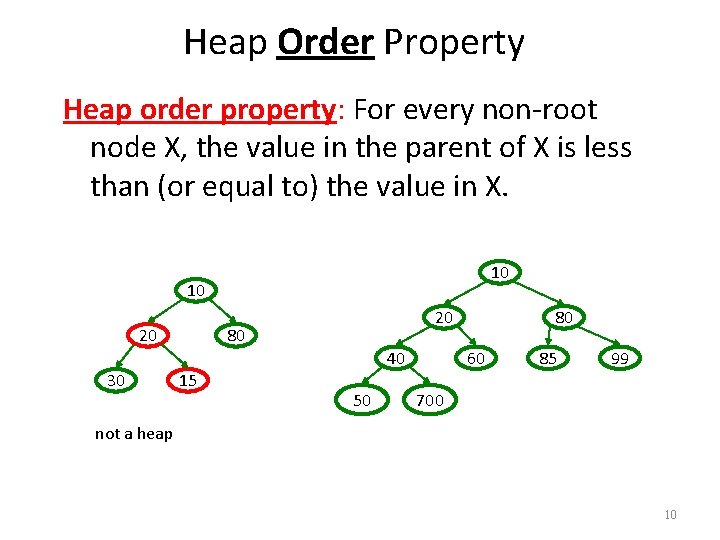
Heap Order Property Heap order property: For every non-root node X, the value in the parent of X is less than (or equal to) the value in X. 10 10 20 20 80 40 30 15 50 80 60 85 99 700 not a heap 10

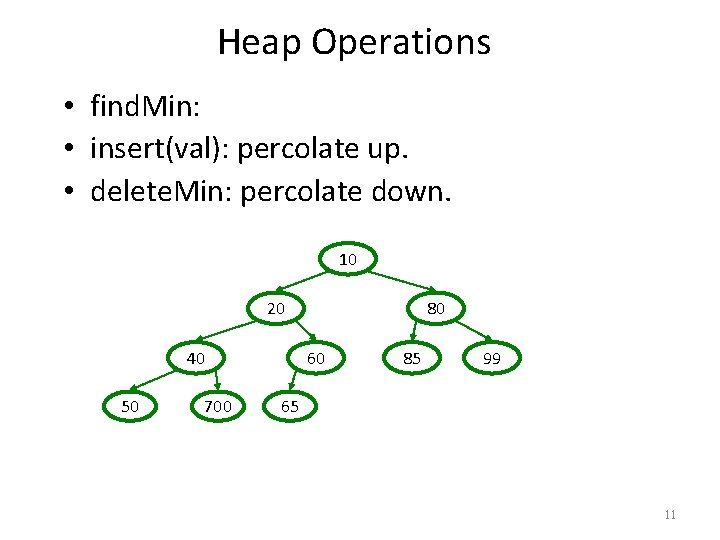
Heap Operations • find. Min: • insert(val): percolate up. • delete. Min: percolate down. 10 20 40 50 700 80 60 85 99 65 11

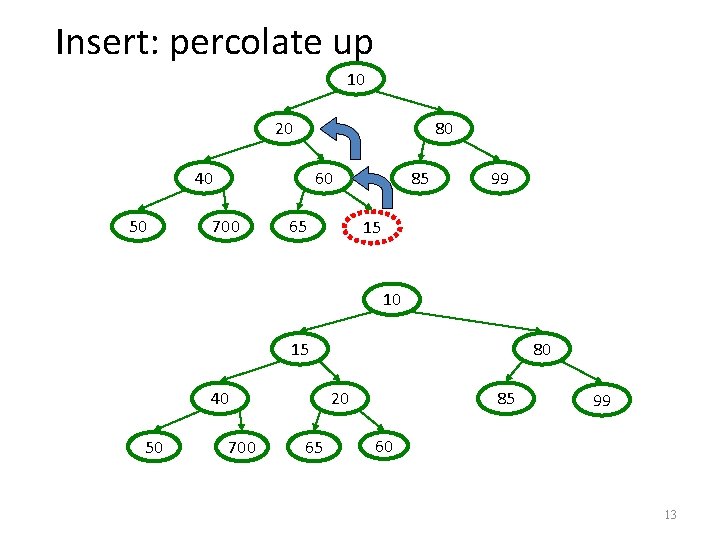
Heap – Insert(val) Basic Idea: 1. Put val at “next” leaf position 2. Percolate up by repeatedly exchanging node until no longer needed 12

Insert: percolate up 10 20 80 40 50 60 700 65 85 99 15 10 15 40 50 700 80 20 65 85 99 60 13

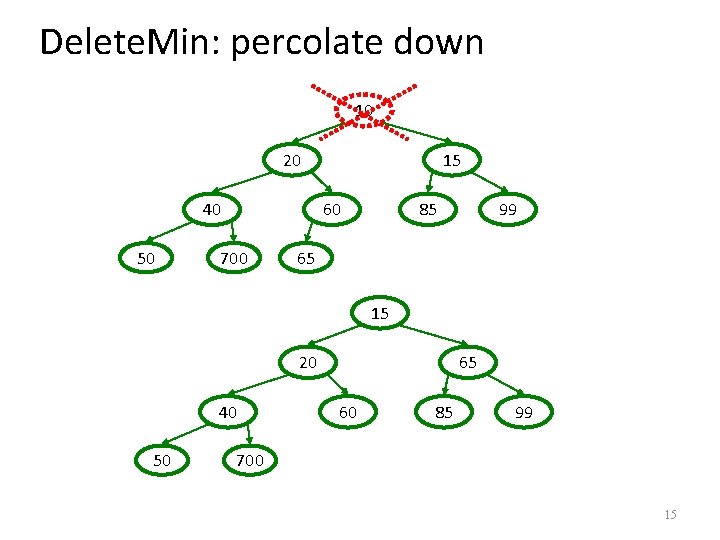
Heap – Delete. Min Basic Idea: 1. Remove root (that is always the min!) 2. Put “last” leaf node at root 3. Find smallest child of node 4. Swap node with its smallest child if needed. 5. Repeat steps 3 & 4 until no swaps needed. 14

Delete. Min: percolate down 10 20 40 50 15 60 700 85 99 65 15 20 40 50 65 60 85 99 700 15

Working on Heaps • What are the two properties of a heap? – Structure Property – Order Property • How do we work on heaps? – Fix the structure – Fix the order 16

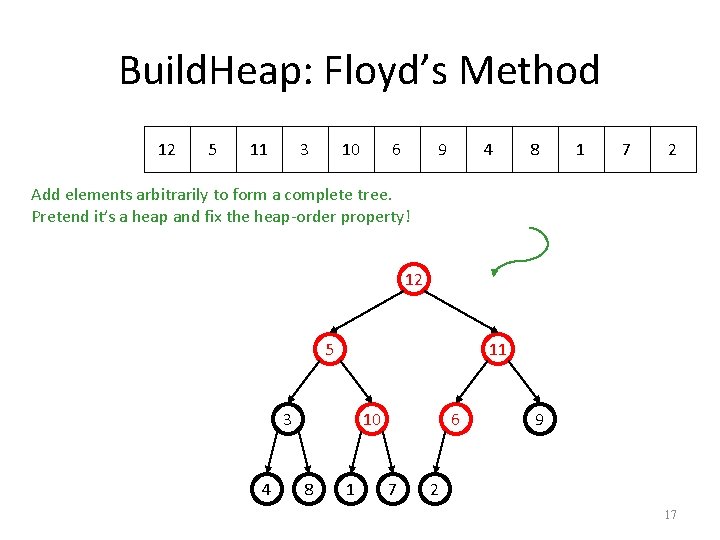
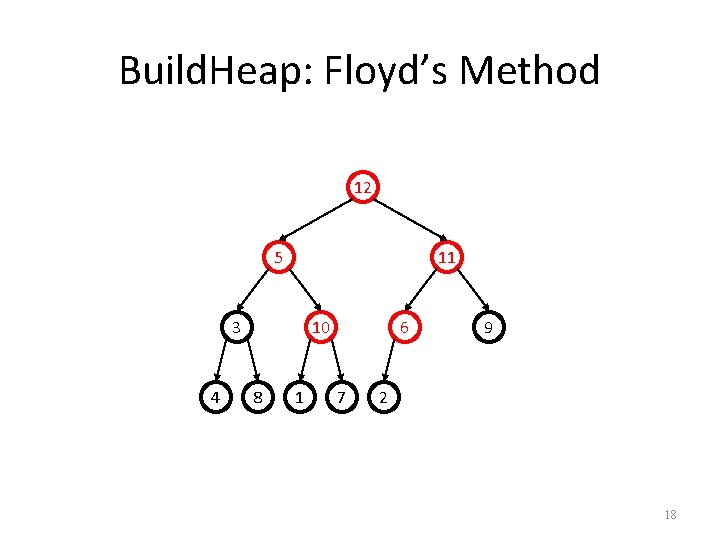
Build. Heap: Floyd’s Method 12 5 11 3 10 6 9 4 8 1 7 2 Add elements arbitrarily to form a complete tree. Pretend it’s a heap and fix the heap-order property! 12 5 11 3 4 10 8 1 6 7 9 2 17

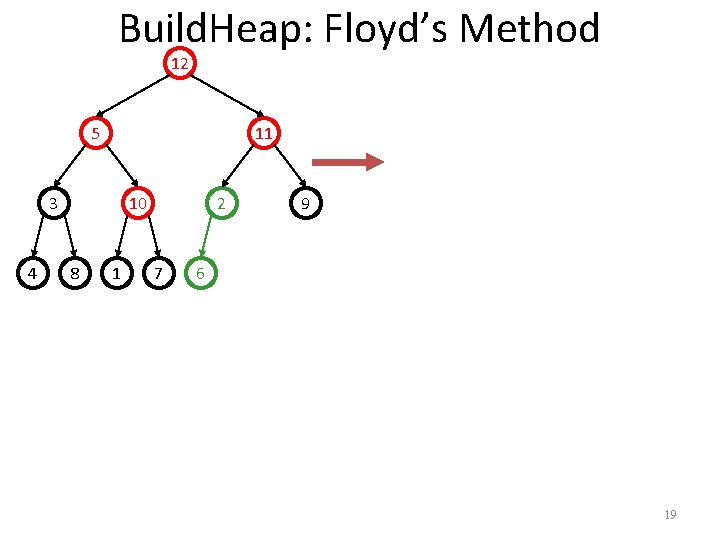
Build. Heap: Floyd’s Method 12 5 11 3 4 10 8 1 6 7 9 2 18

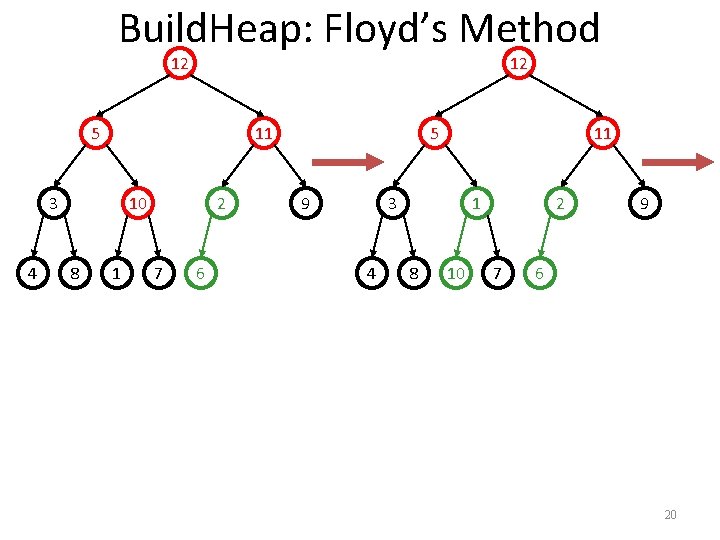
Build. Heap: Floyd’s Method 12 5 11 3 4 10 8 1 2 7 9 6 19

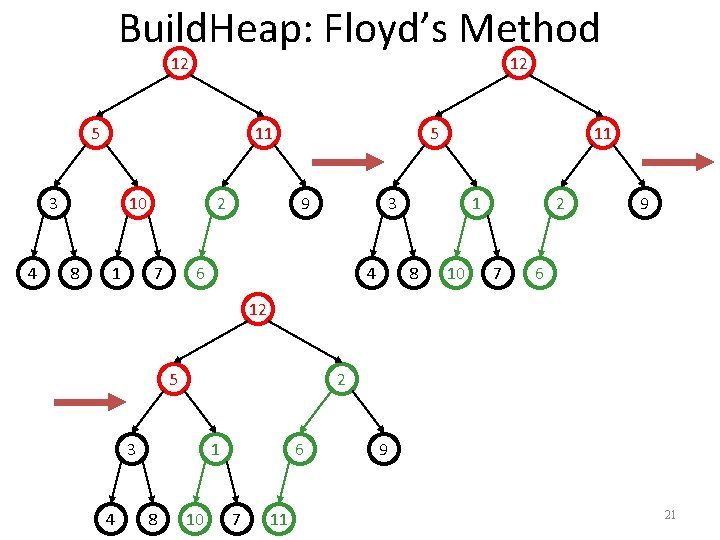
Build. Heap: Floyd’s Method 12 12 5 11 3 4 10 8 1 2 7 6 5 9 11 3 4 1 8 10 2 7 9 6 20

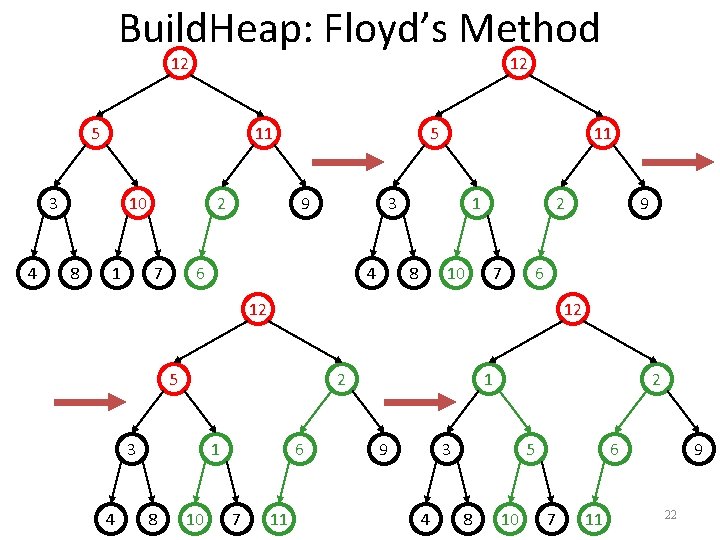
Build. Heap: Floyd’s Method 12 12 5 11 3 4 10 8 1 2 7 5 9 11 3 6 4 1 8 10 2 7 9 6 12 5 2 3 4 1 8 10 6 7 11 9 21

Build. Heap: Floyd’s Method 12 12 5 11 3 4 10 8 1 2 7 5 9 11 3 6 4 1 8 10 2 7 6 12 12 5 2 3 4 1 8 10 6 7 9 11 1 9 2 3 4 5 8 10 6 7 11 9 22

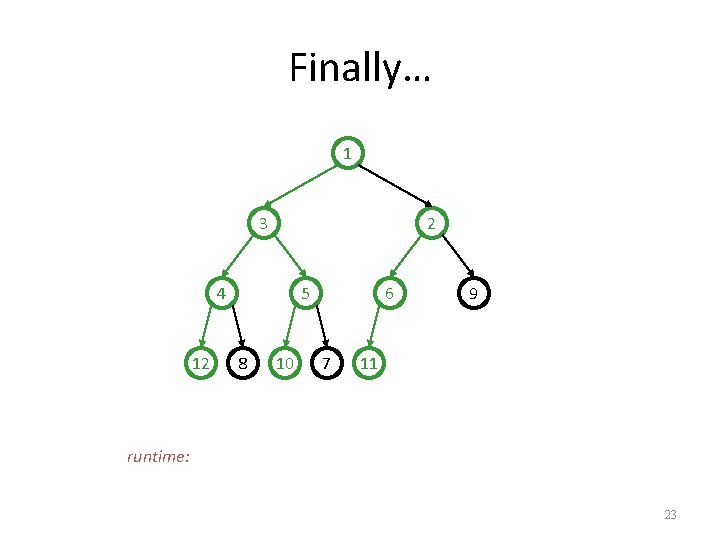
Finally… 1 3 2 4 12 5 8 10 6 7 9 11 runtime: 23

Facts about Heaps Observations: • • Finding a child/parent index is a multiply/divide by two Operations jump widely through the heap Each percolate step looks at only two new nodes Inserts are at least as common as delete. Mins Realities: • Division/multiplication by powers of two are equally fast • Looking at only two new pieces of data: bad for cache! • With huge data sets, disk accesses dominate 24

Buildheap pseudocode private void build. Heap() { for ( int i = current. Size/2; i > 0; i-- ) percolate. Down( i ); } • Adding the items one at a time is O(n log n) in the worst case 25