Implementing a Priority Queue Heaps Priority Queues Recall

Implementing a Priority Queue Heaps

Priority Queues • Recall: 3 Container Adapters • Stack • Queue • Priority Queue – implementation? • Priority Queue • Uses std: : vector • Maintains complete tree w/special ordering property • Vector w/property is Heap

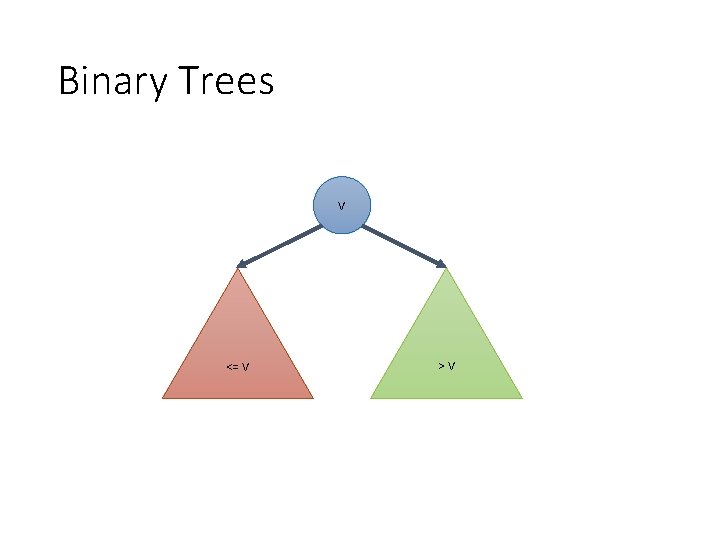
Binary Trees V <= V >V

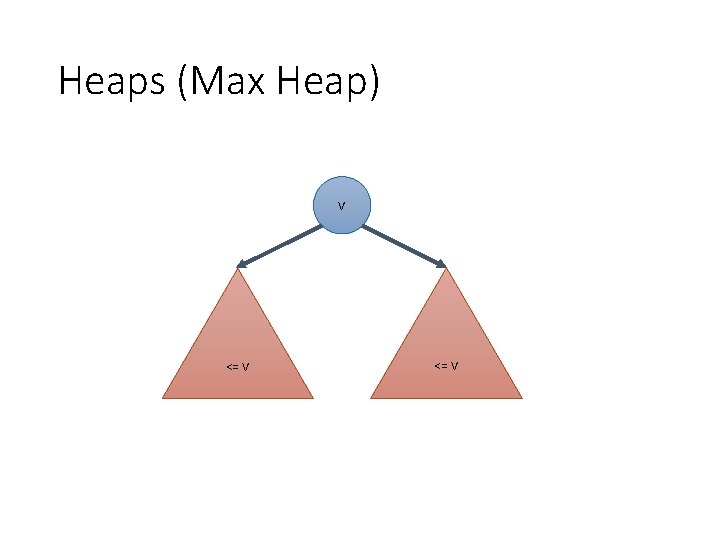
Heaps (Max Heap) V <= V

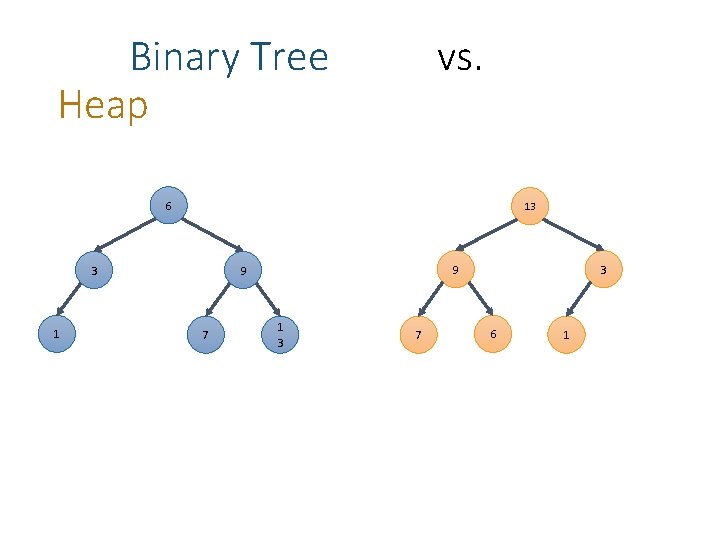
Binary Tree Heap vs. 6 13 3 1 7 3 9 9 1 3 7 6 1

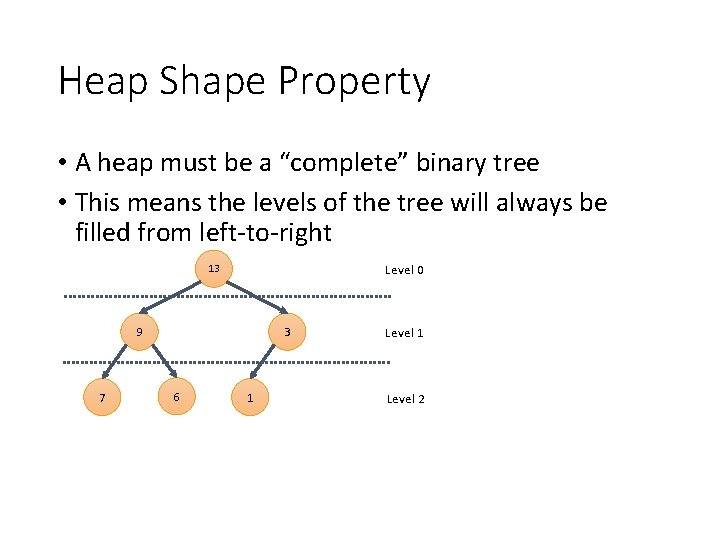
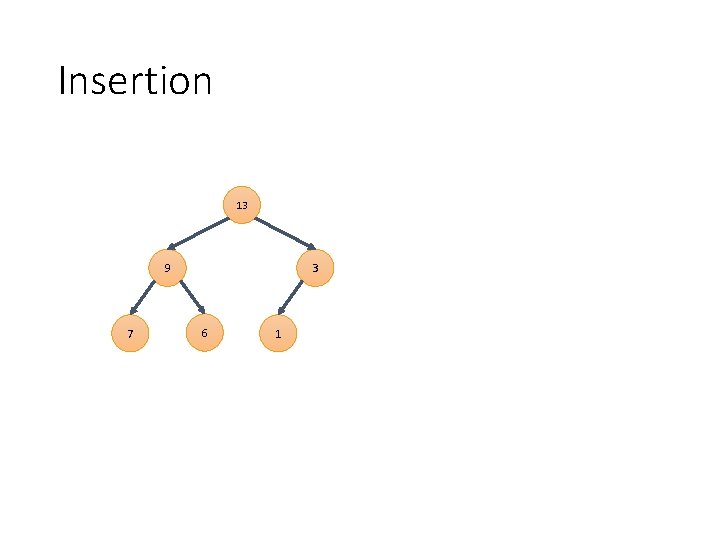
Heap Shape Property • A heap must be a “complete” binary tree • This means the levels of the tree will always be filled from left-to-right Level 0 13 3 9 7 6 1 Level 2

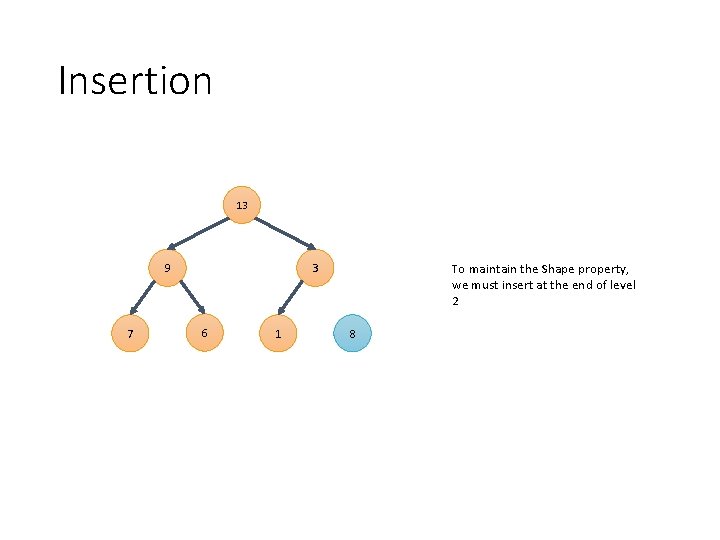
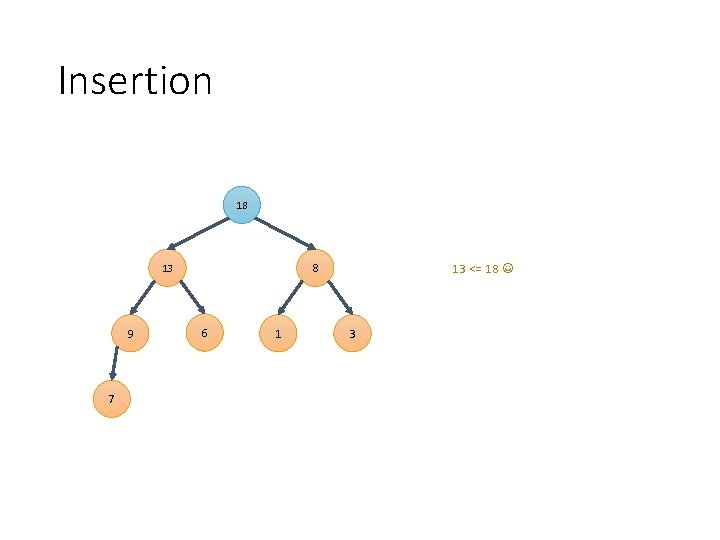
Insertion 13 9 7 3 6 1

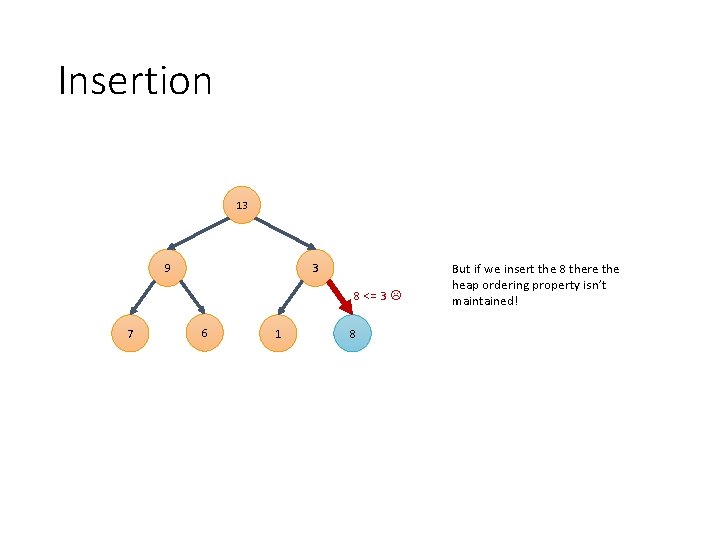
Insertion 13 9 7 3 6 1 To maintain the Shape property, we must insert at the end of level 2 8

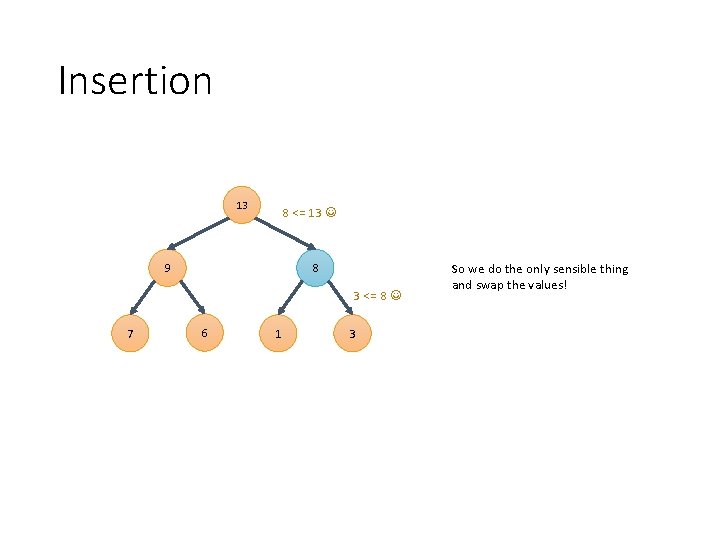
Insertion 13 9 3 8 <= 3 7 6 1 8 But if we insert the 8 there the heap ordering property isn’t maintained!

Insertion 13 8 <= 13 9 8 3 <= 8 7 6 1 3 So we do the only sensible thing and swap the values!

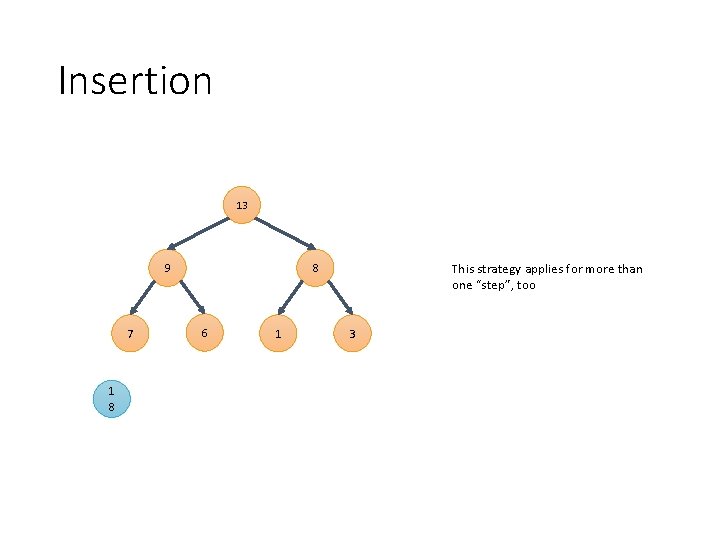
Insertion 13 9 7 1 8 8 6 1 This strategy applies for more than one “step”, too 3

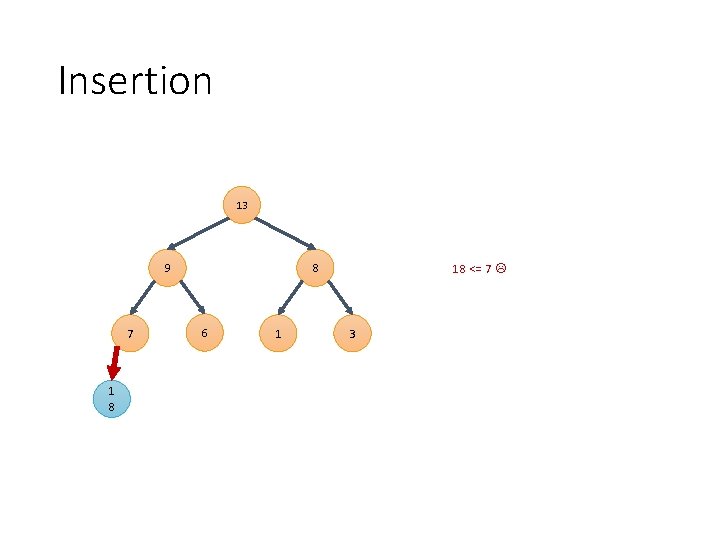
Insertion 13 9 7 1 8 8 6 1 18 <= 7 3

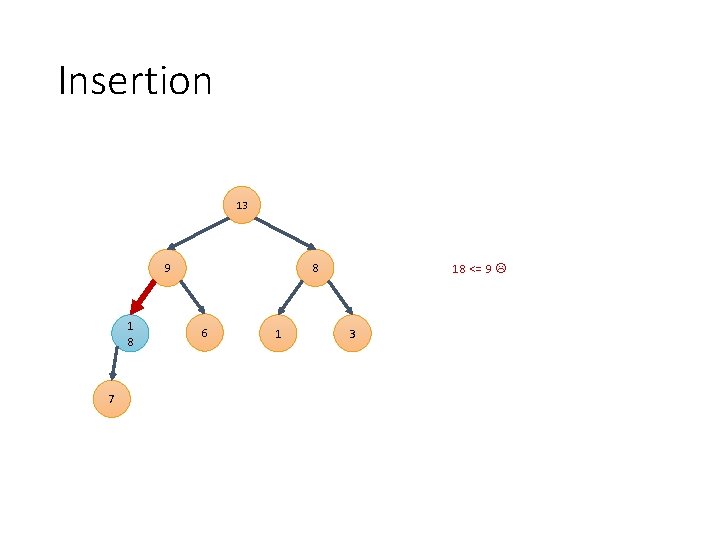
Insertion 13 9 1 8 7 8 6 1 18 <= 9 3

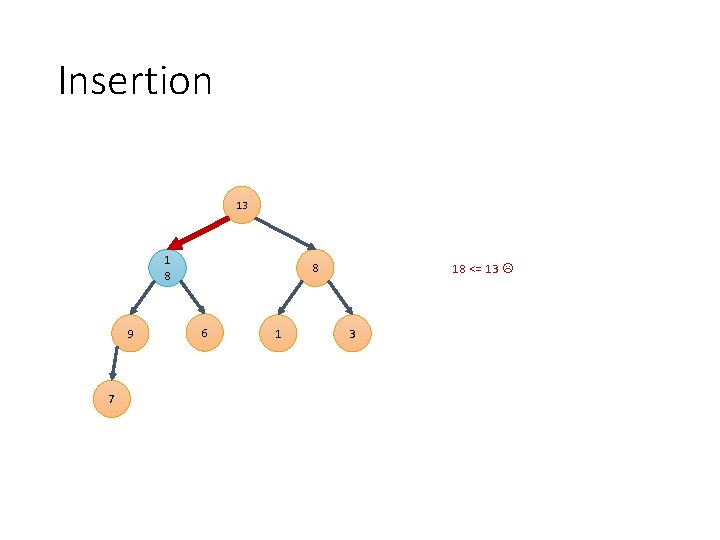
Insertion 13 1 8 9 7 8 6 1 18 <= 13 3

Insertion 18 8 13 9 7 6 1 13 <= 18 3

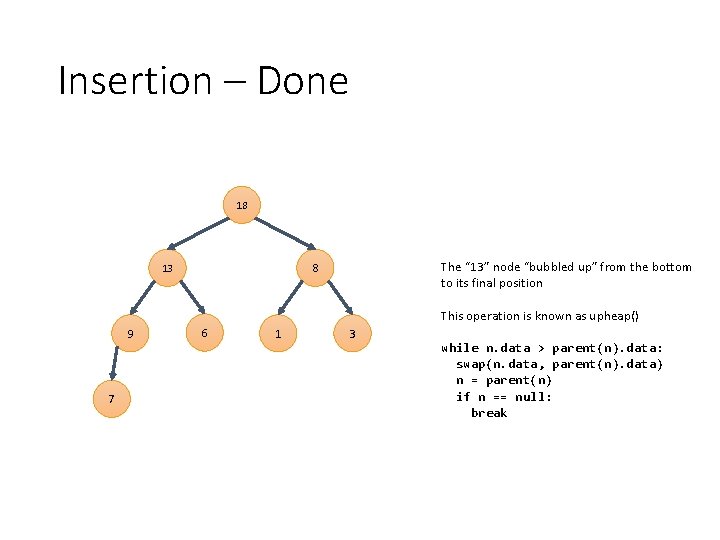
Insertion – Done 18 The “ 13” node “bubbled up” from the bottom to its final position 8 13 This operation is known as upheap() 9 7 6 1 3 while n. data > parent(n). data: swap(n. data, parent(n). data) n = parent(n) if n == null: break

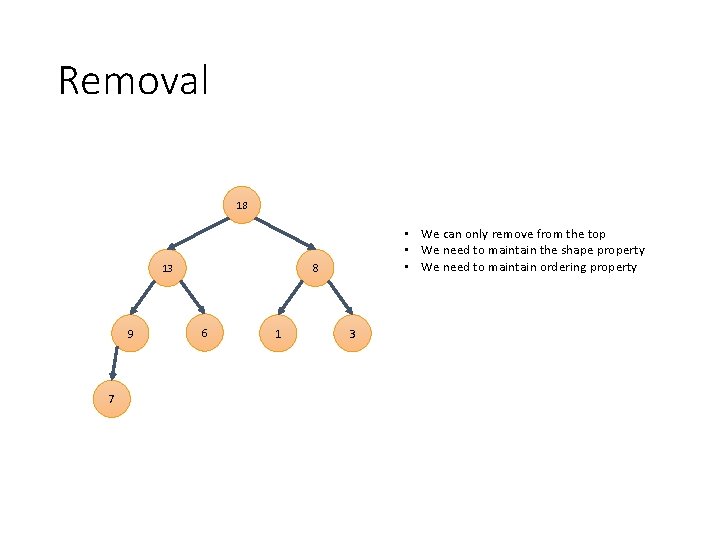
Removal 18 8 13 9 7 • We can only remove from the top • We need to maintain the shape property • We need to maintain ordering property 6 1 3

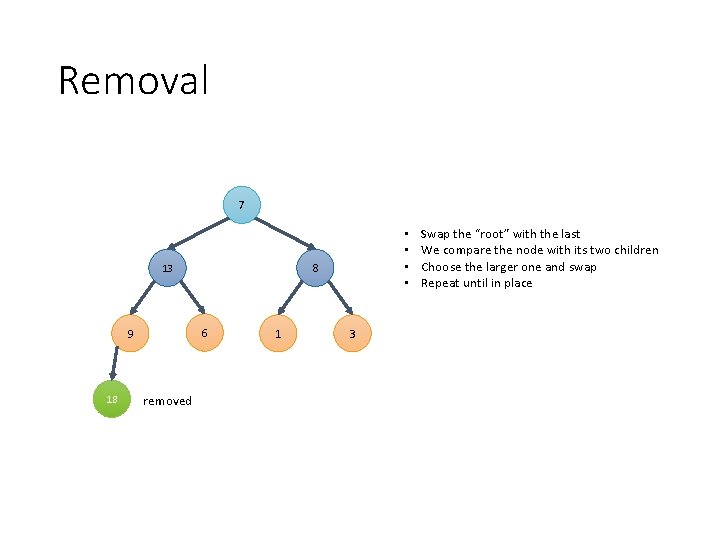
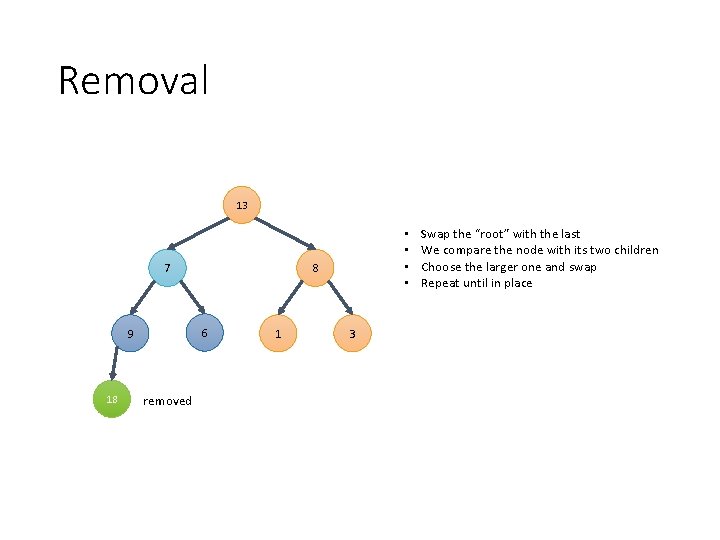
Removal 7 8 13 6 9 18 removed • • 1 3 Swap the “root” with the last We compare the node with its two children Choose the larger one and swap Repeat until in place

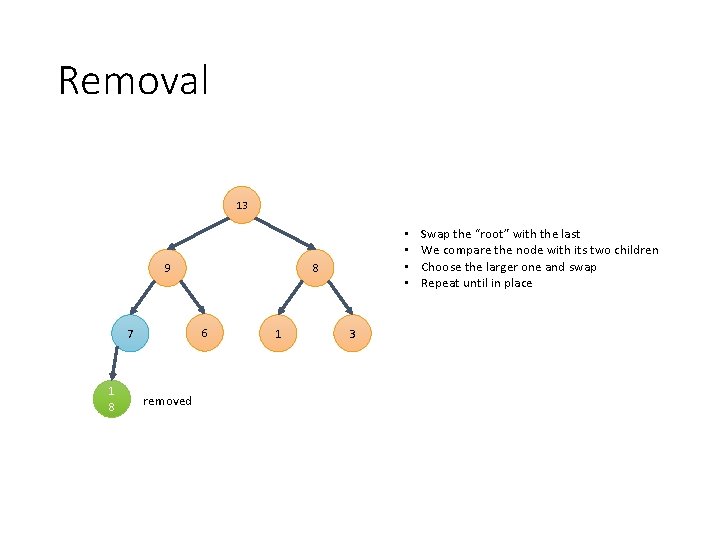
Removal 13 7 18 8 6 9 removed • • 1 3 Swap the “root” with the last We compare the node with its two children Choose the larger one and swap Repeat until in place

Removal 13 9 1 8 8 6 7 removed • • 1 3 Swap the “root” with the last We compare the node with its two children Choose the larger one and swap Repeat until in place

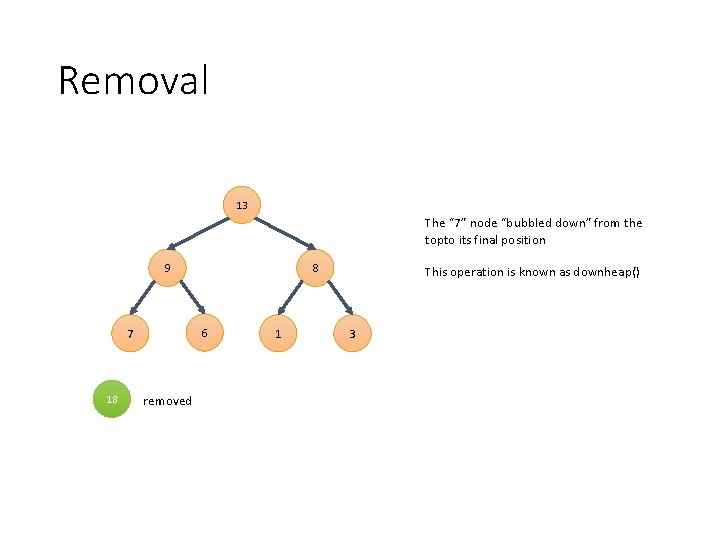
Removal 13 The “ 7” node “bubbled down” from the topto its final position 9 6 7 18 8 removed 1 This operation is known as downheap() 3

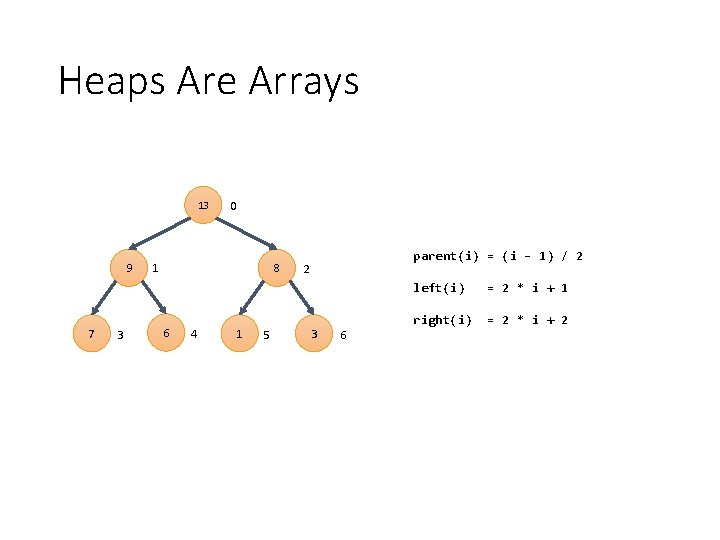
Heaps Are Arrays 13 9 7 3 0 8 1 6 4 1 5 parent(i) = (i – 1) / 2 2 3 6 left(i) = 2 * i + 1 right(i) = 2 * i + 2

Complete Binary Tree Why store tree in vector? parent (i) = p (i) = ? left. Child (i) = lc (i) = ? right. Child (i) = rc (i) = ?

Max and Min Heaps Max Heap property: ( nodes X) [ Value (X) >= Value (Child (X)) ]

priority_queue: : push v. push_back (50);

Upheap (restore heap property) up. Heap (v. size () – 1);

Push void PQ: : push (const T& item) { v. push_back (item); up. Heap (v. size () – 1); }

up. Heap (Helper Method) void PQ: : up. Heap (size_t pos) { T item = v[pos]; size_t i; // Move parent down for (i = pos; i != 0 && item > v[p (i)]; i = p (i)) v[i] = v[p (i)]; // swap unnecessary v[i] = item; }

priority_queue: : pop v. front () = v. back (); v. pop_back (); 18

down. Heap

Pop void PQ: : pop () { v[0] = v. back (); v. pop_back (); // O (1) // Move elem down to proper place down. Heap (0); }

down. Heap (Helper Method) void PQ: : down. Heap (size_t pos) { // Move v[pos] down, max child up size_t i, mc; T val = v[pos]; for (i = pos; (mc = lc (i)) < v. size (); i = mc) { if (mc + 1 < v. size () && v[mc] < v[mc + 1]) ++mc; if (val ? ? ) // Move child up if necessary else ? } // Place val in correct spot }

Heap Sort Overview • Heaps O(N*lg (N)) sort in worst case • Can use heaps to sort in two ways • 1) pq. Sort • Push all elements • Pop and place in vector back to front • Complexity? • 2*Sum (i =1: N) [ lg(i) ]

Heap Sort Overview • 2) True heap sort (better, why? ) • “Heapify” vector (O(N)) • With STL assistance (make_heap) • Roll our own “build. Heap” • elems. To. Place = v. size () - 1 • while (elems. To. Place > 0) • Swap front and back of v • --elems. To. Place • Restore heap property at root (taking into consideration heap is one elem. smaller)

make_heap (STL) int arr[] { 50, 20, 75, 35, 25 }; // Header <algorithm> make_heap (arr, arr + 5);

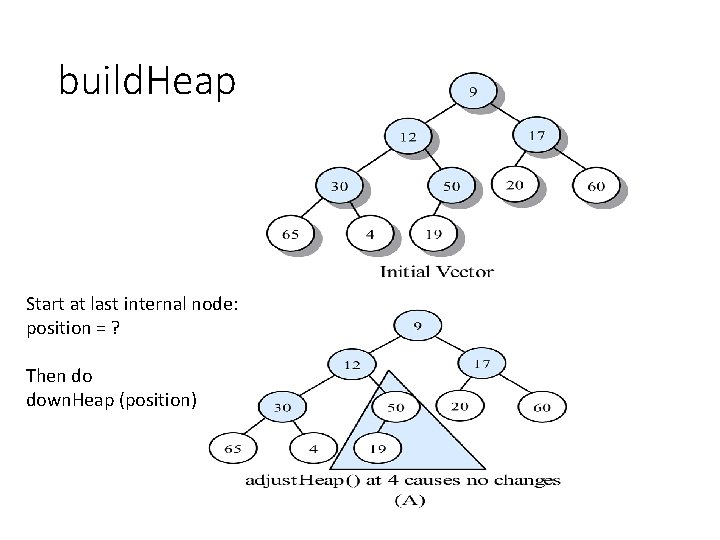
build. Heap • Potential algorithms (several don’t work!) • Call down. Heap (0) N times • Call down. Heap (i) varying i from 0 to N-1 • Call down. Heap (i) varying i from N-1 to 0 • Call up. Heap (i) varying i from 0 to N-1 • Call up. Heap (i) varying i from N-1 to 0

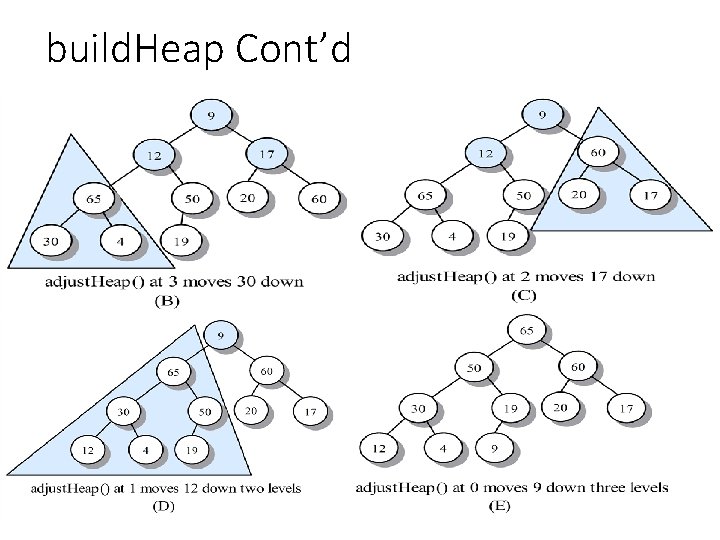
build. Heap Start at last internal node: position = ? Then do down. Heap (position)

build. Heap Cont’d

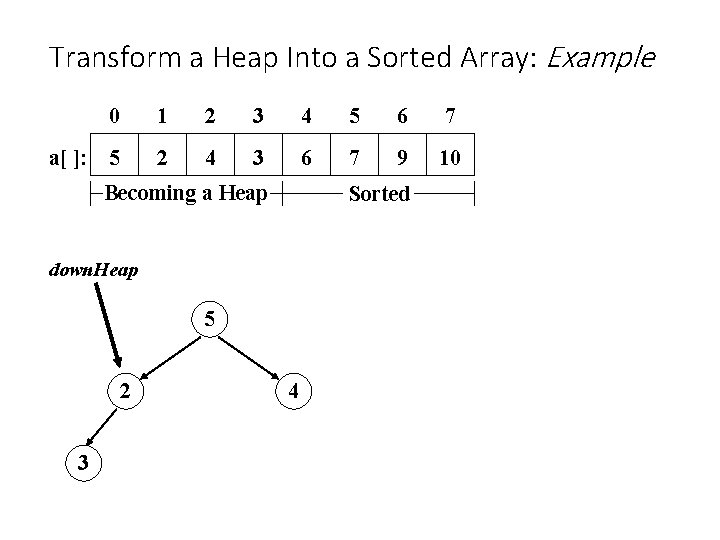
Heap Sorted Vector • Now convert heap to sorted vector • Swap front and back • Decrease size of heap by 1 • downheap (0)

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 10 9 6 7 2 4 5 3 Heap 10 • Heap is in a[0. . 7] and the sorted region is empty 9 7 3 6 2 4 • Swap front and back 5

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 3 9 6 7 2 4 5 10 Semiheap Sorted down. Heap • a[0. . 6] now represents a semiheap 3 9 7 • a[7] is the sorted region 6 2 4 5

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 9 3 6 7 2 4 5 10 Becoming a Heap down. Heap 9 3 7 6 2 4 5 Sorted

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 9 7 6 3 2 4 5 10 Heap Sorted 9 7 3 6 2 4 5

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 5 7 6 3 2 4 9 10 Semiheap Sorted down. Heap 5 7 3 6 2 4

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 7 5 6 3 2 4 9 10 Heap Sorted down. Heap 7 5 3 6 2 4

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 4 5 6 3 2 7 9 10 Semiheap Sorted down. Heap 4 5 3 6 2

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 6 5 4 3 2 7 9 10 Heap Sorted 6 5 3 4 2

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 2 5 4 3 6 7 9 10 Semiheap Sorted down. Heap 2 5 3 4

Transform a Heap Into a Sorted Array: Example 0 1 2 3 4 5 6 7 a[ ]: 5 2 4 3 6 7 9 10 Becoming a Heap Sorted down. Heap 5 2 3 4

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 5 3 4 2 6 7 9 10 Heap Sorted 5 3 2 4

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 2 3 4 5 6 7 9 10 Semiheap Sorted down. Heap 2 3 4

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 4 3 2 5 6 7 9 10 Heap Sorted 4 3 2

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 2 3 4 5 6 7 9 10 Semiheap Sorted down. Heap 2 3

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 3 2 4 5 6 7 9 10 Heap 3 2 Sorted

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 2 3 4 5 6 7 9 10 Heap 2 Sorted

Heap Sorted Vector 0 1 2 3 4 5 6 7 a[ ]: 2 3 4 5 6 7 9 10 Sorted

Heap Sort (Code) // Create heap from vector bottom up // Start with last internal node // O(N) for “for” loop for (i = (N – 2) / 2; i >= 0; --i) down. Heap (i); // O(N lg(N)) for “while” while (N > 1) { swap (v[0], v[N-1]); --N; down. Heap (0); }