Priority Queues Heaps Leftist Trees CSE POSTECH Priority

Priority Queues, Heaps & Leftist Trees CSE, POSTECH

Priority Queues l l l 2 A priority queue is a collection of zero or more elements each element has a priority or value Unlike the FIFO queues, the order of deletion from a priority queue (e. g. , who gets served next) is determined by the element priority Elements are deleted by increasing or decreasing order of priority rather than by the order in which they arrived in the queue

Priority Queues l Operations performed on priority queues 1) Find an element, 2) insert a new element, 3) delete an element, etc. l l 3 Two kinds of (Min, Max) priority queues exist In a Min priority queue, find/delete operation finds/deletes the element with minimum priority In a Max priority queue, find/delete operation finds/deletes the element with maximum priority Two or more elements can have the same priority

Priority Queues l l 4 See ADT 12. 1 & Program 12. 1 for max priority queue specification What would be different for min priority queue specification? Read Examples 12. 1, 12. 2 What are other examples in our daily lives that utilize the priority queue concept?

Implementation of Priority Queues l Implemented using heaps and leftist trees l Heap is a complete binary tree that is efficiently stored using the array-based representation l Leftist tree is a linked data structure suitable for the implementation of a priority queue 5

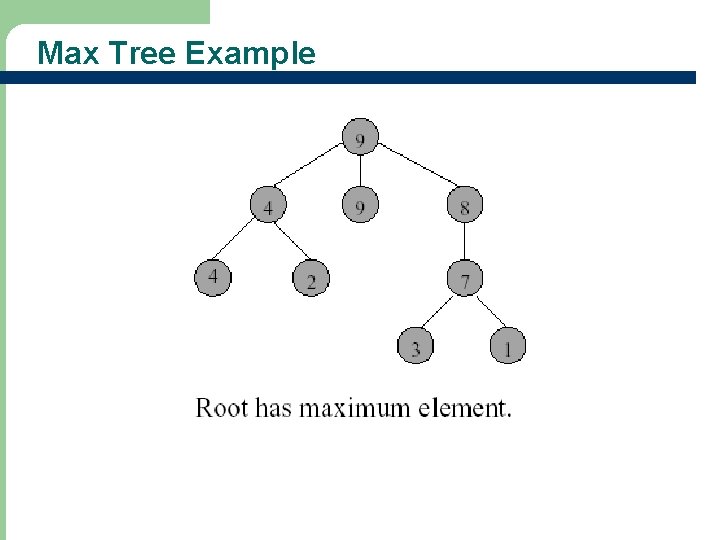
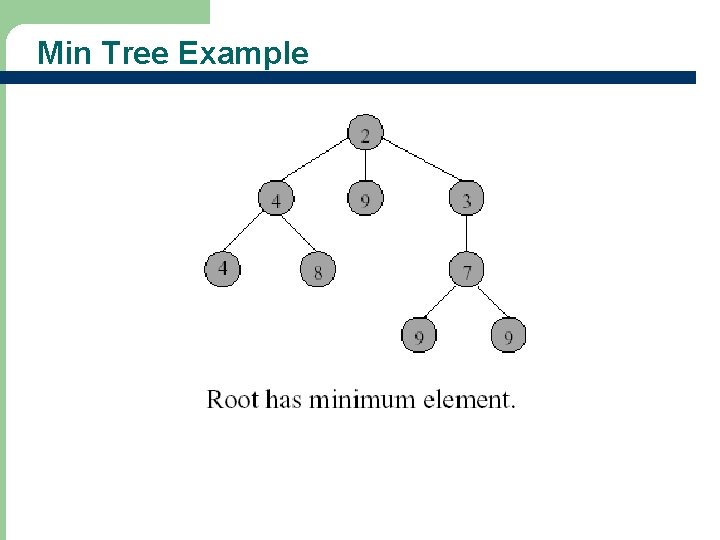
Max (Min) Tree l A max tree (min tree) is a tree in which the value in each node is greater (less) than or equal to those in its children (if any) – – 6 See Figure 12. 1, 12. 2 for examples Nodes of a max or min tree may have more than two children (i. e. , may not be binary tree)

Max Tree Example 7

Min Tree Example 8

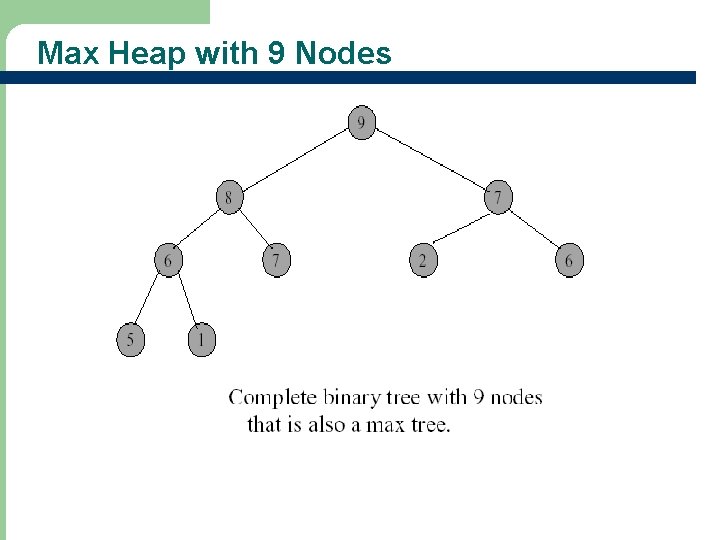
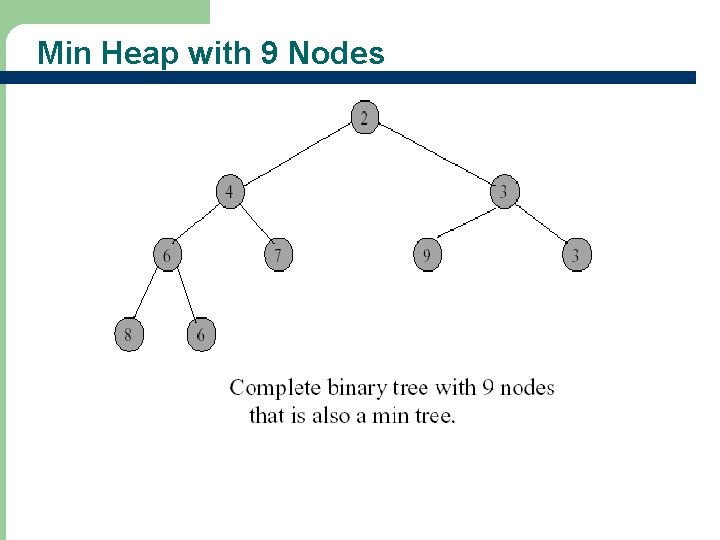
Heaps - Definitions l A max heap (min heap) is a max (min) tree that is also a complete binary tree – – Figure 12. 1 (a) & (c) are max heap Figure 12. 2 (a) & (c) are min heap Why aren’t Figure 12. 1 (b) & 12. 2 (b) max/min heap? How can you change the Figure 12. 1 (b) & 12. 2 (b) so that they are max/min heap? 14 9 12 10 9 7 8 6 6 5 30 25

Max Heap with 9 Nodes 10

Min Heap with 9 Nodes 11

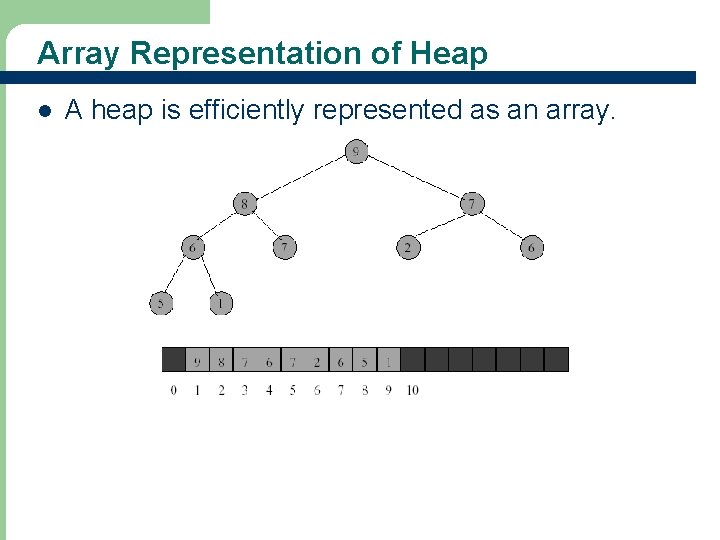
Array Representation of Heap l 12 A heap is efficiently represented as an array.

Heap Operations When n is the number of elements (heap size), l Insertion O(log 2 n) l Deletion O(log 2 n) l Initialization O(n) 13

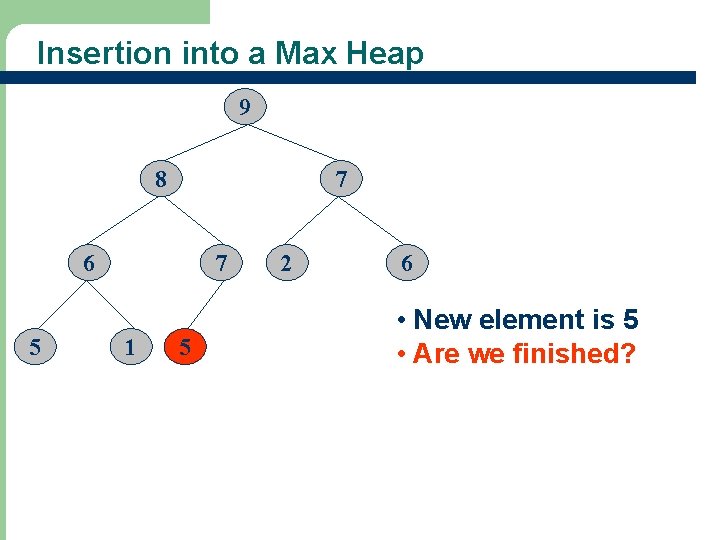
Insertion into a Max Heap 9 8 7 6 5 14 7 1 5 2 6 • New element is 5 • Are we finished?

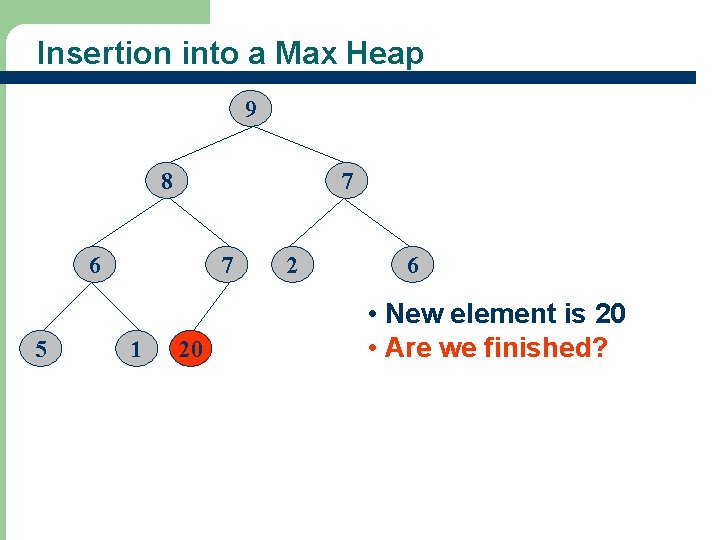
Insertion into a Max Heap 9 8 7 6 5 15 7 1 20 2 6 • New element is 20 • Are we finished?

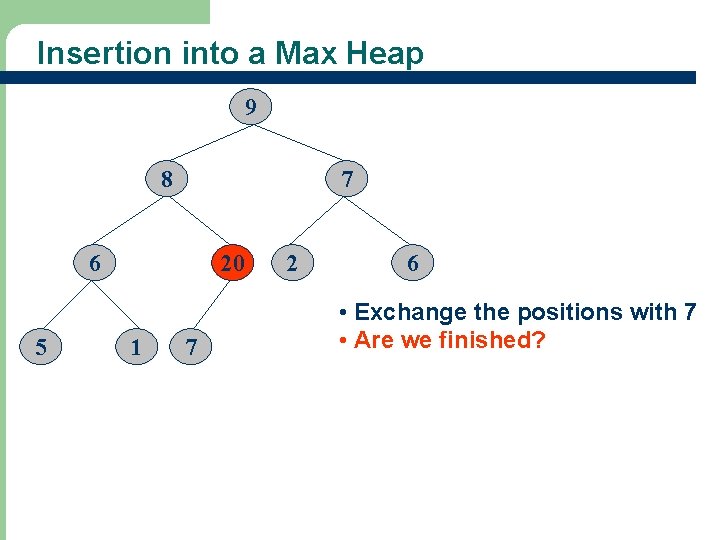
Insertion into a Max Heap 9 8 7 6 5 16 20 1 7 2 6 • Exchange the positions with 7 • Are we finished?

Insertion into a Max Heap 9 20 7 6 5 17 8 1 7 2 6 • Exchange the positions with 8 • Are we finished?

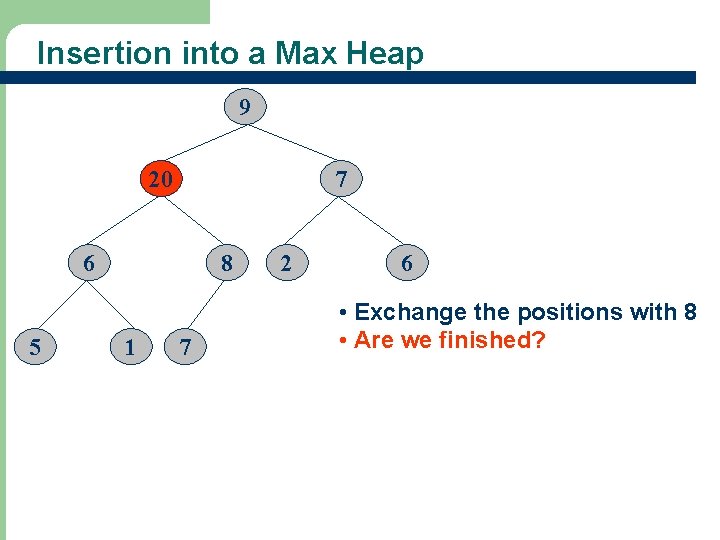
Insertion into a Max Heap 20 9 7 6 5 18 8 1 7 2 6 • Exchange the positions with 9 • Are we finished?

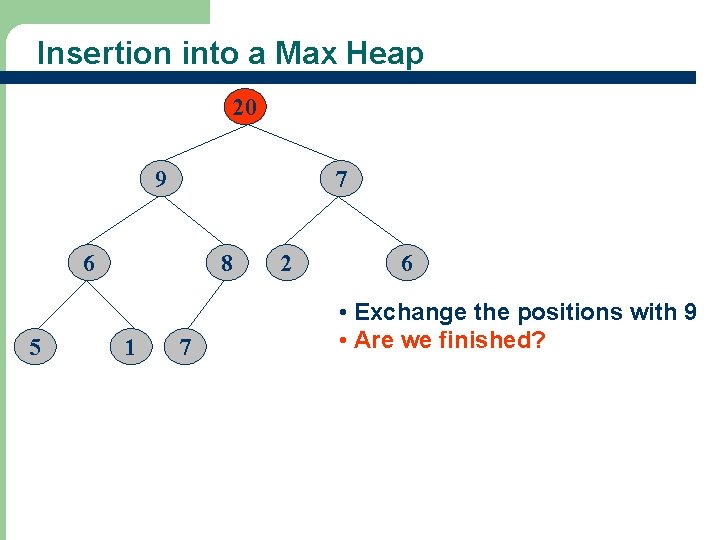
Complexity of Insertion l See also Figure 12. 3 for another insertion example l At each level, we do (1) work Thus the time complexity is O(height) = O(log 2 n), where n is the heap size l 19

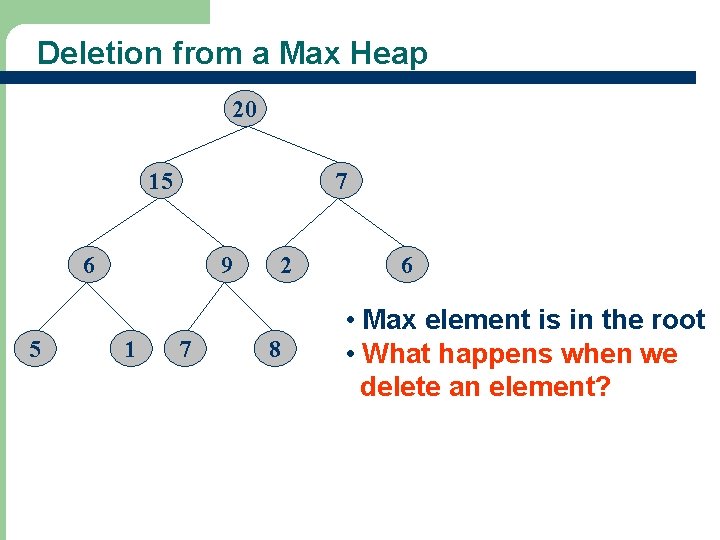
Deletion from a Max Heap 20 15 7 6 5 20 9 1 7 2 8 6 • Max element is in the root • What happens when we delete an element?

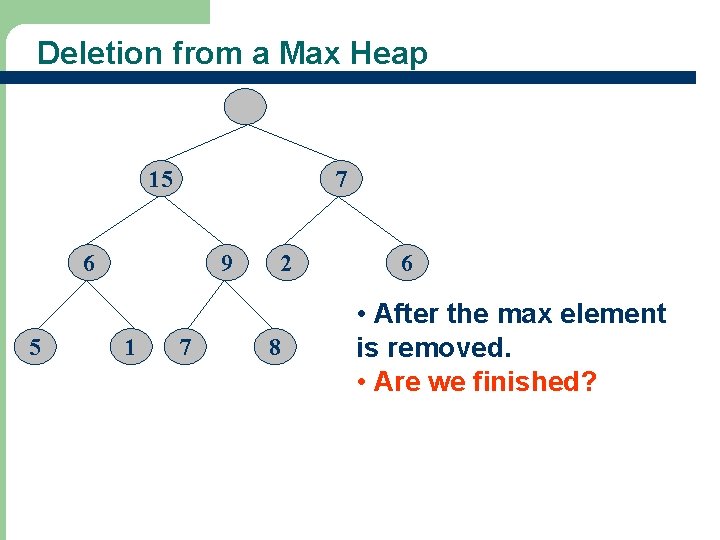
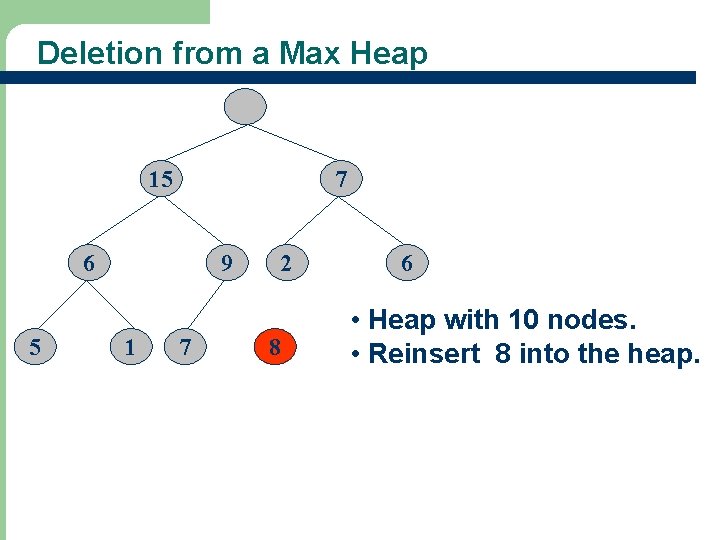
Deletion from a Max Heap 15 7 6 5 21 9 1 7 2 8 6 • After the max element is removed. • Are we finished?

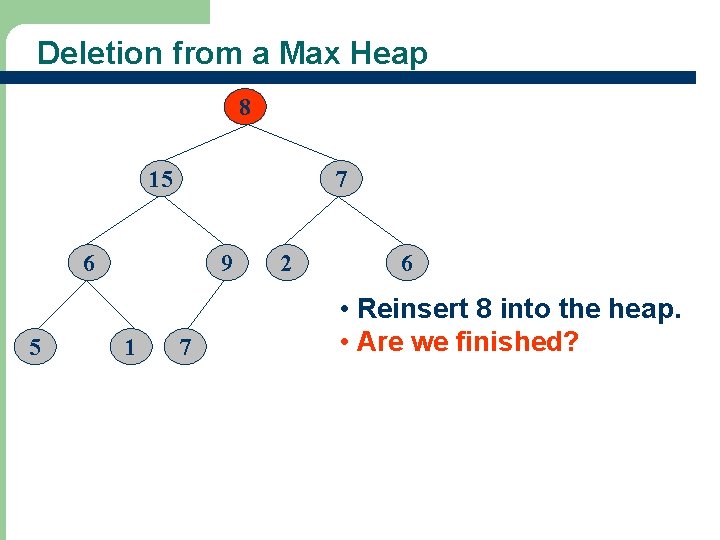
Deletion from a Max Heap 15 7 6 5 22 9 1 7 2 8 6 • Heap with 10 nodes. • Reinsert 8 into the heap.

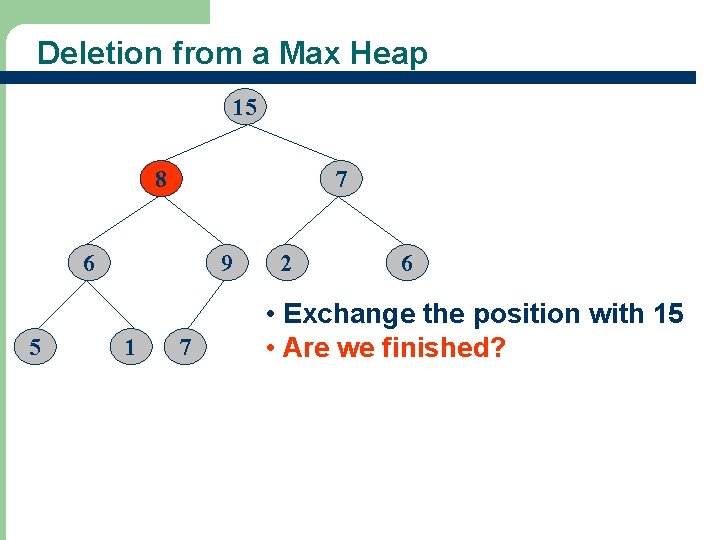
Deletion from a Max Heap 8 15 7 6 5 23 9 1 7 2 6 • Reinsert 8 into the heap. • Are we finished?

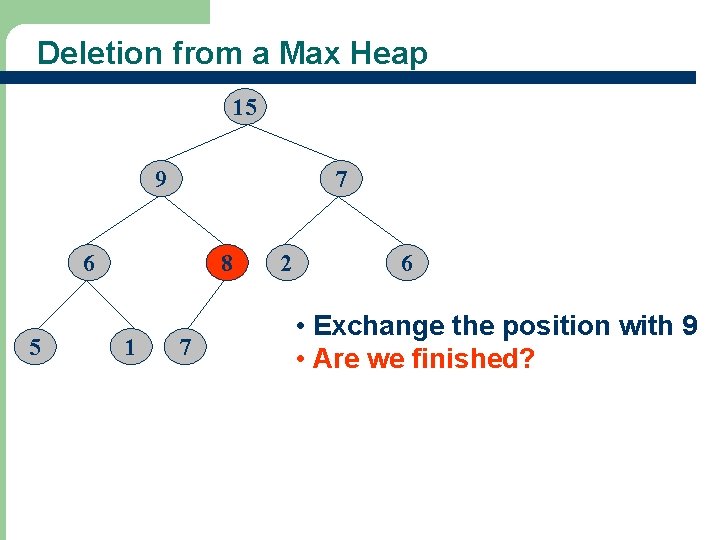
Deletion from a Max Heap 15 8 7 6 5 24 9 1 7 2 6 • Exchange the position with 15 • Are we finished?

Deletion from a Max Heap 15 9 7 6 5 25 8 1 7 2 6 • Exchange the position with 9 • Are we finished?

Complexity of Deletion l See also Figure 12. 4 for another deletion example l The time complexity of deletion is the same as insertion At each level, we do (1) work Thus the time complexity is O(height) = O(log 2 n), where n is the heap size l l 26

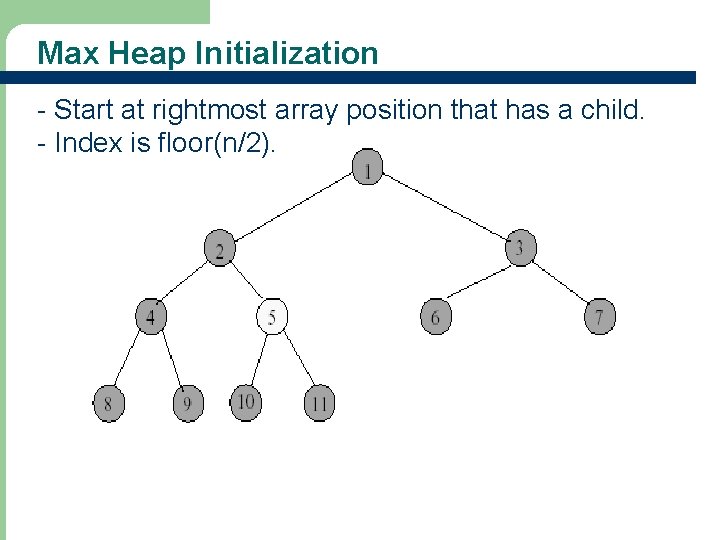
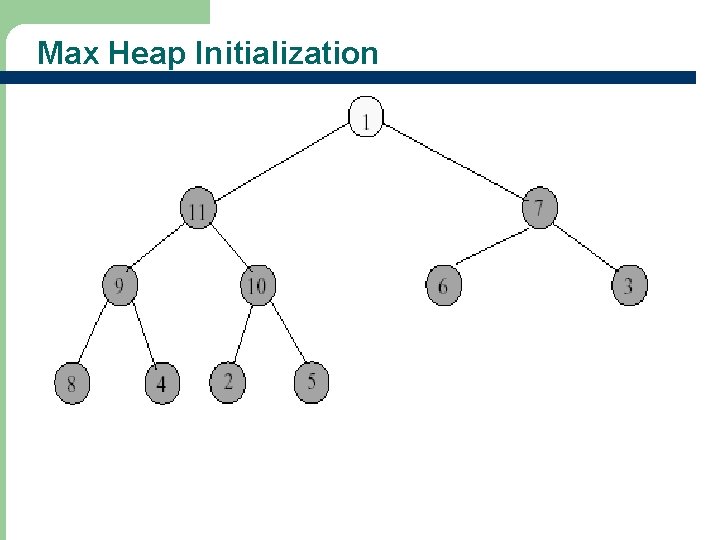
Max Heap Initialization • Heap initialization means to construct a heap by adjusting the tree if necessary • Example: input array = [-, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11] 27

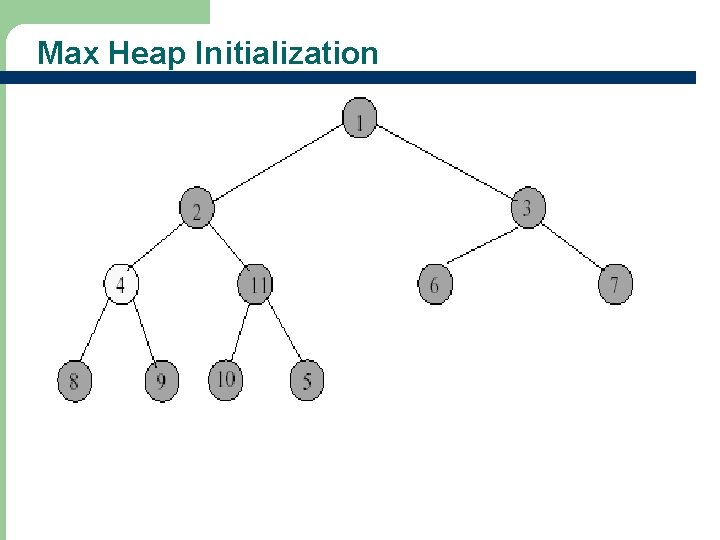
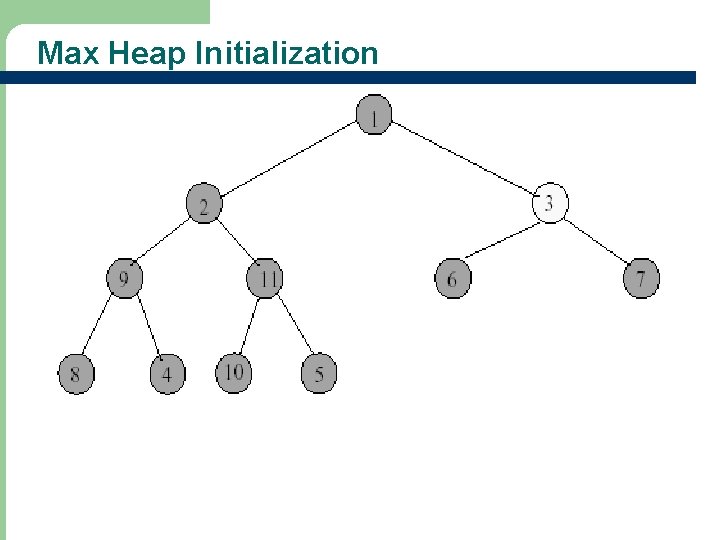
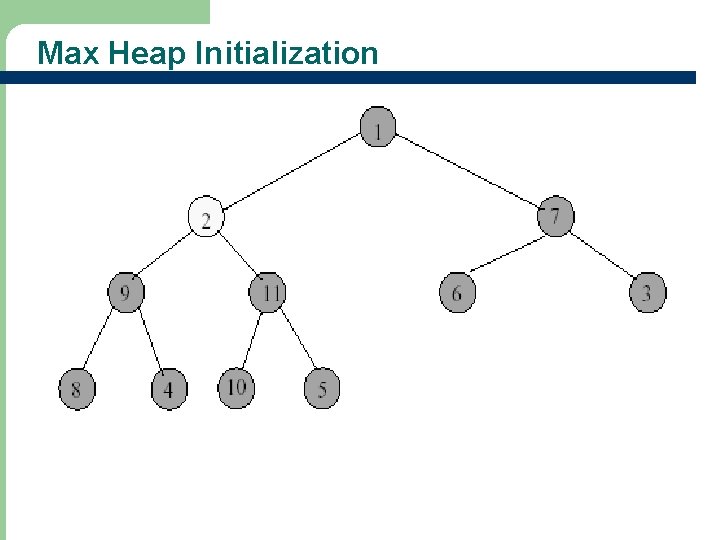
Max Heap Initialization - Start at rightmost array position that has a child. - Index is floor(n/2). 28

Max Heap Initialization 29

Max Heap Initialization 30

Max Heap Initialization 31

Max Heap Initialization 32

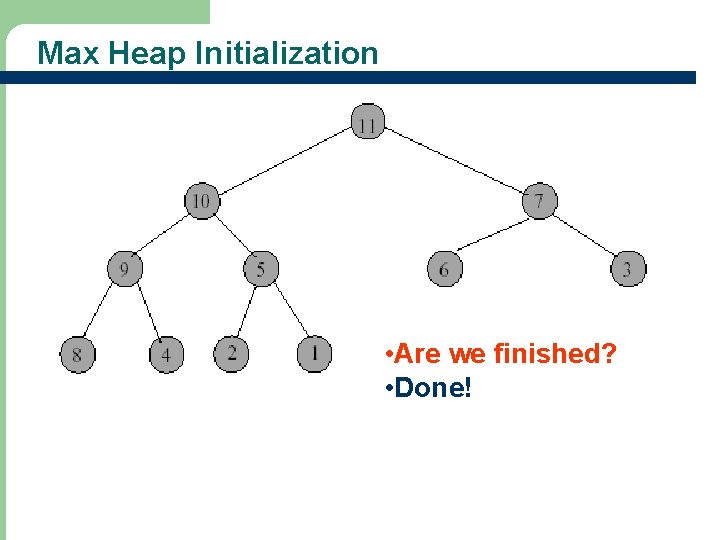
Max Heap Initialization • Are we finished? • Done! 33

Complexity of Initialization • See Figure 12. 5 for another initialization example • Height of heap = h. • Number of nodes at level j is <= 2 j-1. • Time for each node at level j is O(h-j+1). • Time for all nodes at level j is <= 2 j-1(h-j+1) = t(j). • Total time is t(1) + t(2) + … + t(h) = O(2 h) = O(n). 34

The Class Max. Heap l l l 35 See Program 12. 2 for Insertion into a Max. Heap See Program 12. 3 for Deletion from a Max. Heap See Program 12. 4 for Initializing a nonempty Max. Heap

PUSH OPERATION template<class T> void max. Heap<T>: : push(const T& the. Element) {// Add the. Element to heap. // increase array length if necessary if (heap. Size == array. Length - 1) {// double array length change. Length 1 D(heap, array. Length, 2 * array. Length); array. Length *= 2; } // find place for the. Element // current. Node starts at new leaf and moves up tree int current. Node = ++heap. Size; while (current. Node != 1 && heap[current. Node / 2] < the. Element) { // cannot put the. Element in heap[current. Node] = heap[current. Node / 2]; // move element down current. Node /= 2; // move to parent } heap[current. Node] = the. Element; } 36

POP OPERATION template<class T> void max. Heap<T>: : pop() {// Remove max element. // if heap is empty return null if (heap. Size == 0) // heap empty throw queue. Empty(); // Delete max element heap[1]. ~T(); // Remove last element and reheapify T last. Element = heap[heap. Size--]; // find place for last. Element starting at root int current. Node = 1, child = 2; // child of current. Node while (child <= heap. Size) { // heap[child] should be larger child of current. Node if (child < heap. Size && heap[child] < heap[child + 1]) child++; // can we put last. Element in heap[current. Node]? if (last. Element >= heap[child]) break; // yes // no heap[current. Node] = heap[child]; // move child up current. Node = child; // move down a level child *= 2; 37} } heap[current. Node] = last. Element;

INITIALIZE template<class T> void max. Heap<T>: : initialize(T *the. Heap, int the. Size) {// Initialize max heap to element array the. Heap[1: the. Size]. delete [] heap; heap = the. Heap; heap. Size = the. Size; // heapify for (int root = heap. Size / 2; root >= 1; root--) { T root. Element = heap[root]; // find place to put root. Element int child = 2 * root; // parent of child is target // location for root. Element while (child <= heap. Size) { // heap[child] should be larger sibling if (child < heap. Size && heap[child] < heap[child + 1]) child++; // can we put root. Element in heap[child/2]? if (root. Element >= heap[child]) break; // yes // no heap[child / 2] = heap[child]; // move child up child *= 2; // move down a level } heap[child / 2] = root. Element; } } 38

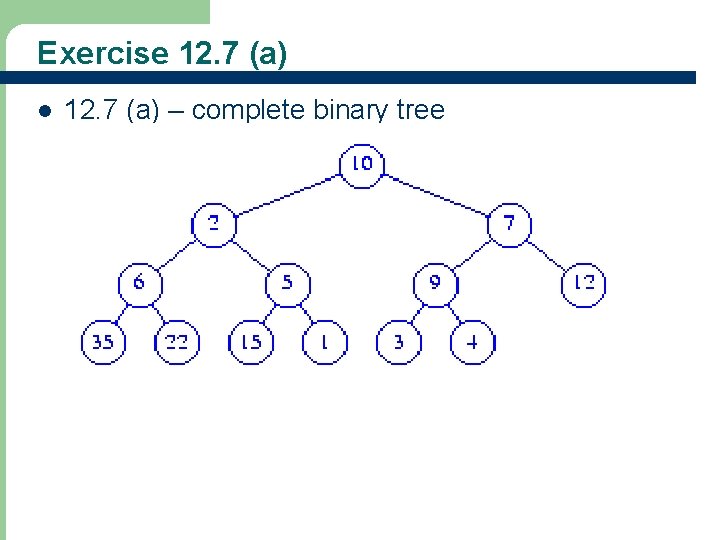
Exercise 12. 7 l Do Exercise 12. 7 – 39 the. Heap = [-, 10, 2, 7, 6, 5, 9, 12, 35, 22, 15, 1, 3, 4]

Exercise 12. 7 (a) l 40 12. 7 (a) – complete binary tree

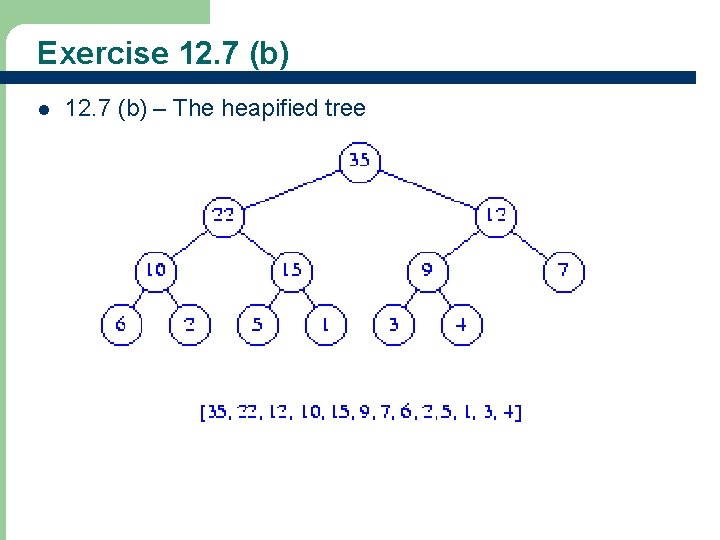
Exercise 12. 7 (b) l 41 12. 7 (b) – The heapified tree

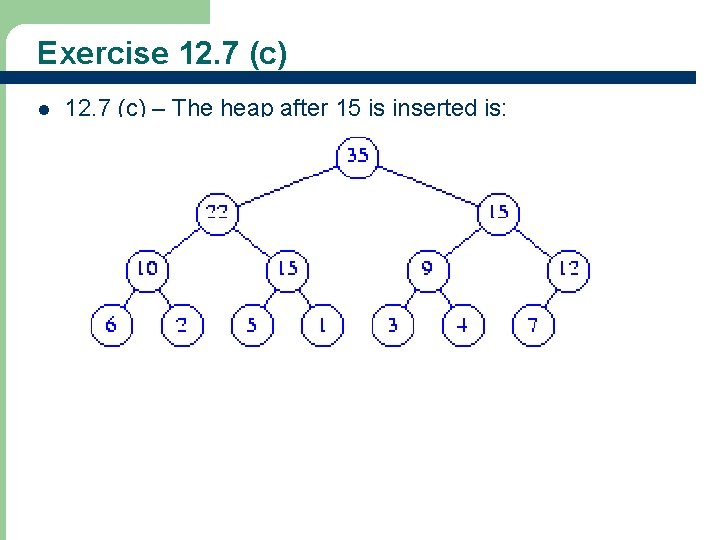
Exercise 12. 7 (c) l 42 12. 7 (c) – The heap after 15 is inserted is:

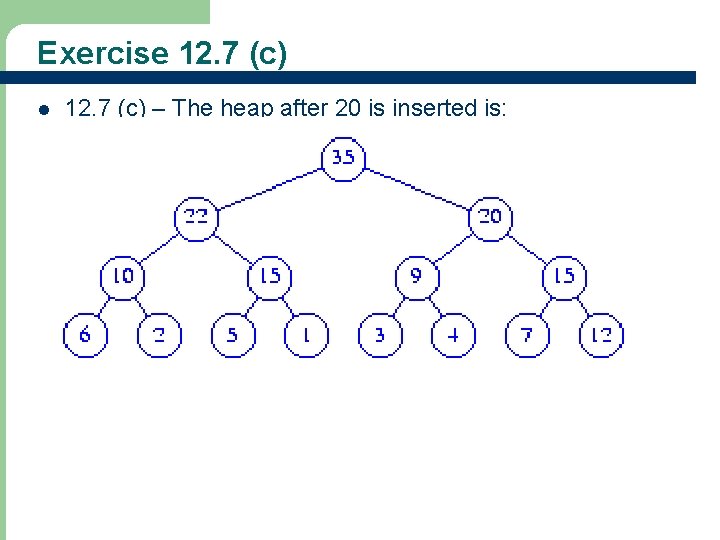
Exercise 12. 7 (c) l 43 12. 7 (c) – The heap after 20 is inserted is:

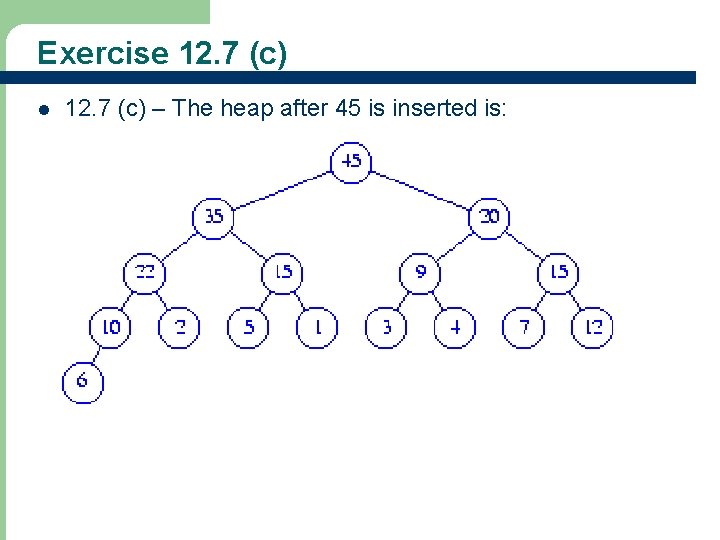
Exercise 12. 7 (c) l 44 12. 7 (c) – The heap after 45 is inserted is:

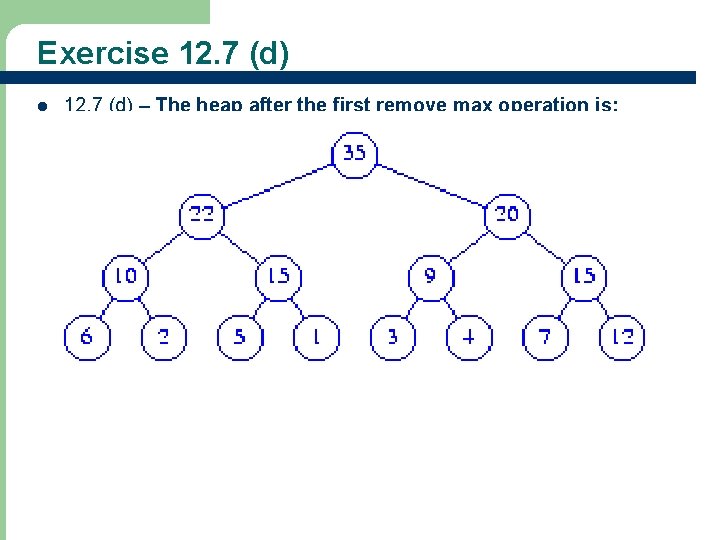
Exercise 12. 7 (d) l 45 12. 7 (d) – The heap after the first remove max operation is:

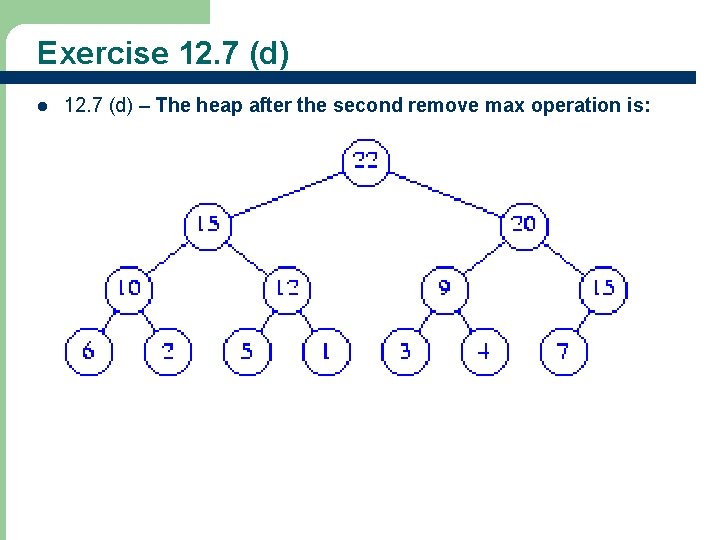
Exercise 12. 7 (d) l 46 12. 7 (d) – The heap after the second remove max operation is:

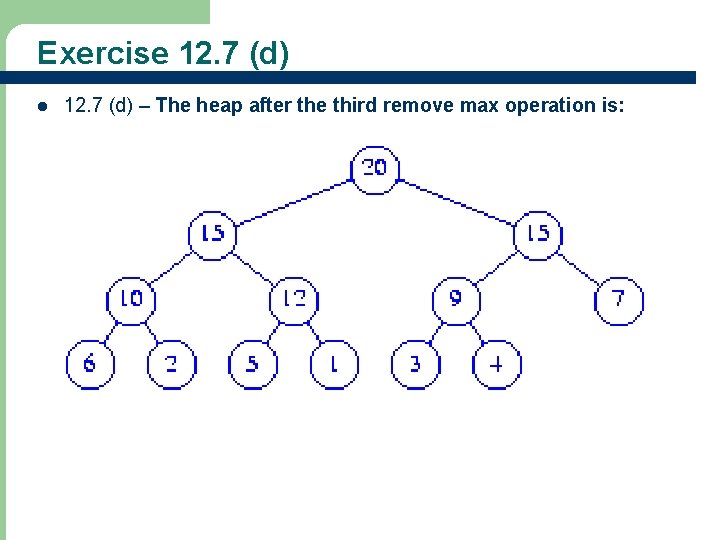
Exercise 12. 7 (d) l 47 12. 7 (d) – The heap after the third remove max operation is:

Leftist Trees l l Despite heap structure being both space and time efficient, it is NOT suitable for all applications of priority queues Leftist tree structures are useful for applications – – l l 48 to meld (i. e. , combine) pairs of priority queues using multiple queues of varying size Leftist tree is a linked data structure suitable for the implementation of a priority queue A tree which tends to “lean” to the left.

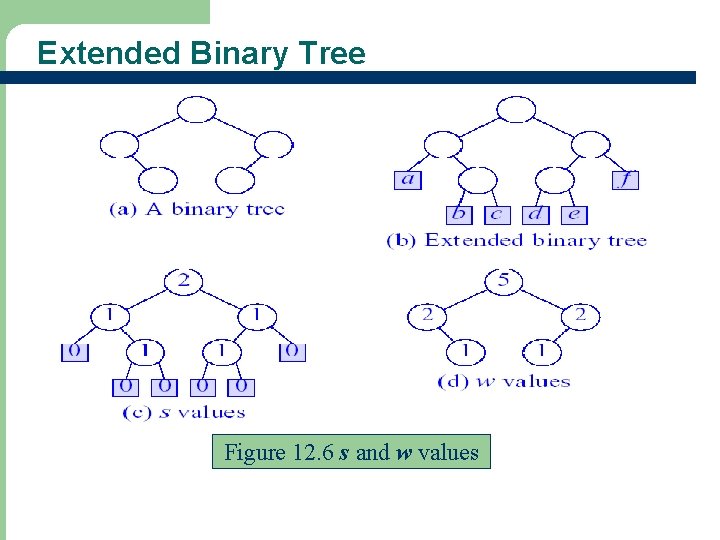
Leftist Trees l l l 49 External node – a special node that replaces each empty subtree Internal node – a node with non-empty subtrees Extended binary tree – a binary tree with external nodes added (see Figure 12. 6)

Extended Binary Tree Figure 12. 6 s and w values 50

Height-Biased Leftist Tree (HBLT) l l l 51 Let s(x) be the length (height) of a shortest path from node x to an external node in its subtree If x is an external node, s(x) = 0 If x is an internal node, s(x) = min {s(L), s(R)} + 1, where L and R are left and right children of x A binary tree is a height-biased leftist tree (HBLT) iff at every internal node, the s value of the left child is greater than or equal to the s value of the right child Is Figure 12. 6(a) an HBLT? If not, how can we change it to become an HBLT?

Max/Min HBLT l A max HBLT is an HBLT that is also a max tree – – l A min HBLT is an HBLT that is also a min tree – – 52 Are the trees of Figure 12. 1 are also max HBLTs? YES! Are the trees of Figure 12. 2 are also min HBLTs? YES!

Weight-Biased Leftist Tree (WBLT) l l 53 Let the weight, w(x), of node x to be the number of internal nodes in the subtree with root x If x is an external node, w(x) = 0 If x is an internal node, its weight is one more than the sum of the weights of its children A binary tree is a weight-biased leftist tree (WBLT) iff at every internal node, the w value of the left child is greater than or equal to the w value of the right child

Weight-Biased Leftist Tree (WBLT) l l l 54 A max (min) WBLT is a max (min) tree that is also a WBLT Is Figure 12. 6(a) an WBLT? If not, how can we change it to become an WBLT?

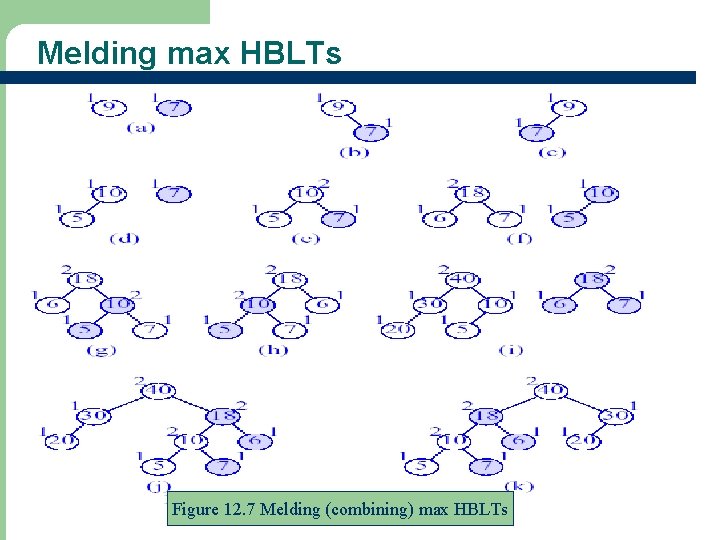
Operations on a Max HBLT l l l 55 Read Section 12. 5. 2 for Insertion into a Max HBLT Read Section 12. 5. 3 for Deletion from a Max HBLT Read Section 12. 5. 4 for Melding Two Max HBLTs See Figure 12. 7 and read Example 12. 3 for Melding max HBLTs Read Section 12. 5. 5 for Initialization of a Max HBLT See Figure 12. 8 for Initializing a max HBLT

Melding max HBLTs 56 Figure 12. 7 Melding (combining) max HBLTs

The Class max. HBLT l See Program 12. 5 for Melding of two leftist trees See Program 12. 6 for meld, push and pop methods See Program 12. 7 for Initializing a max HBLT l Do Exercise 12. 19 l l 57

Exercise 12. 19 (a) The first six calls to meld create the following six max leftist trees. 5 7 3 20 6 15 9 8 2 12 30 17 The next three calls to meld combine pairs of these trees to create the following three trees: 20 7 5 6 3 What would be next? 58 30 9 8 2 15 17 12

Applications of Heaps l l l 59 Sort (heap sort) Machine scheduling Huffman codes

Heap Sort use element key as priority Algorithm l put elements to be sorted into a priority queue (i. e. , initialize a heap) l extract (delete) elements from the priority queue l – – 60 if a min priority queue is used, elements are extracted in non-decreasing order of priority if a max priority queue is used, elements are extracted in non-increasing order of priority

Heap Sort Example l 61 After putting into a max priority queue

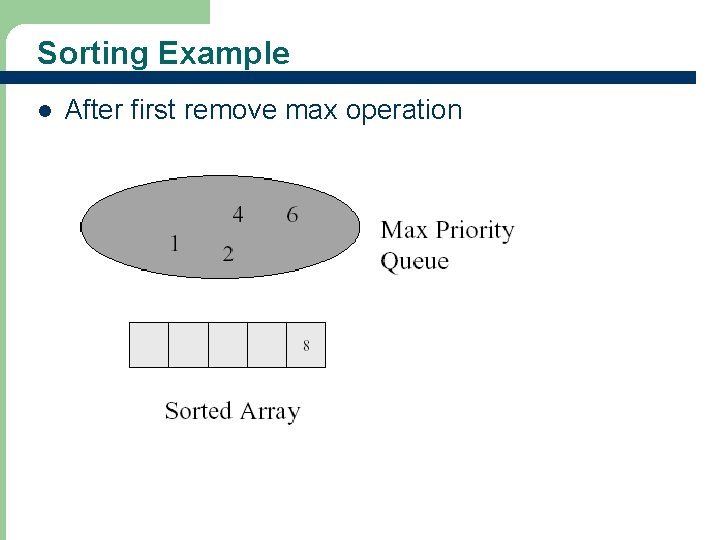
Sorting Example l 62 After first remove max operation

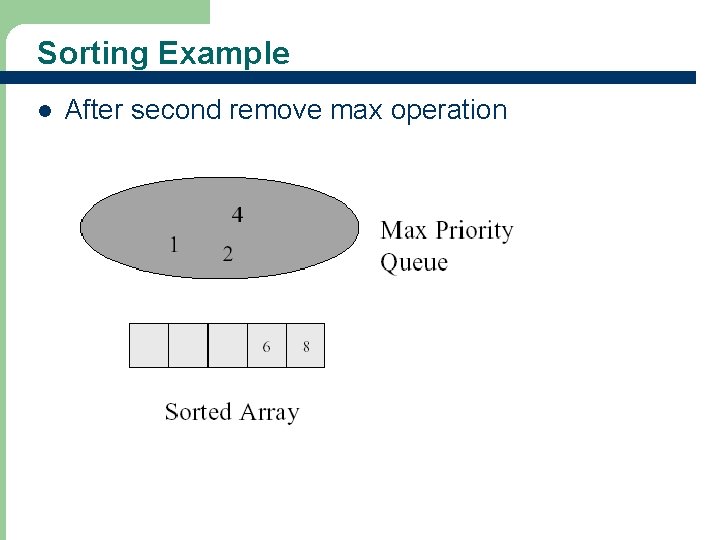
Sorting Example l 63 After second remove max operation

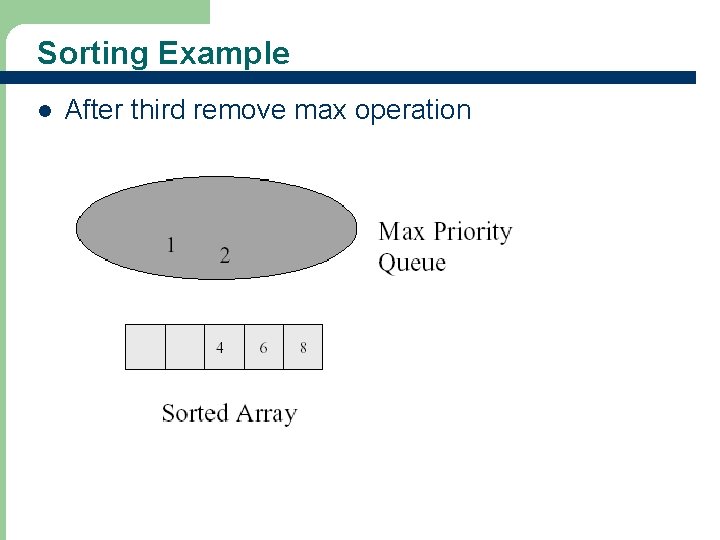
Sorting Example l 64 After third remove max operation

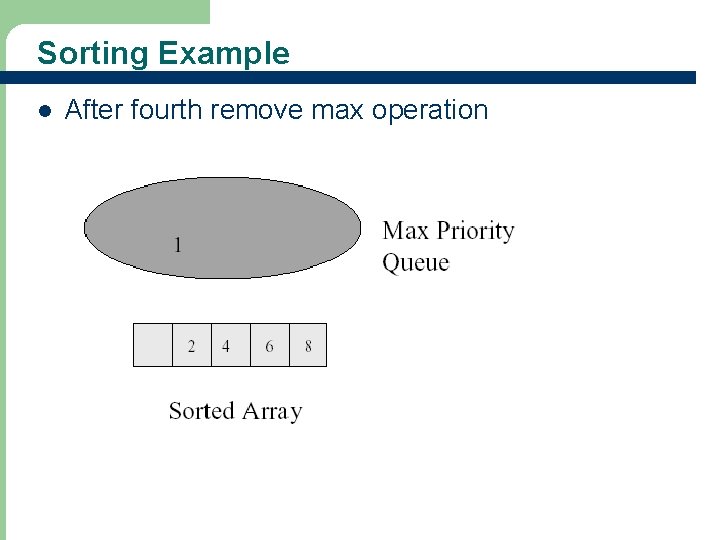
Sorting Example l 65 After fourth remove max operation

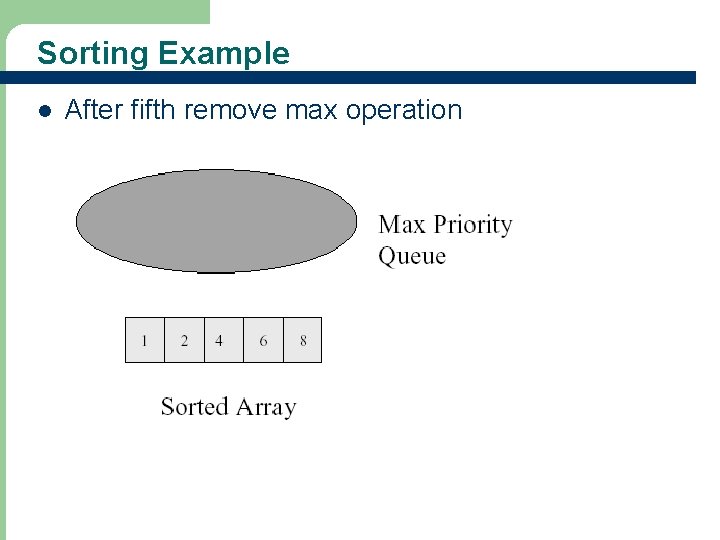
Sorting Example l 66 After fifth remove max operation

Complexity Analysis of Heap Sort l See Program 12. 8 for Heap Sort See Figure 12. 9 for another Heap Sort example l Heap sort n elements. l – – – Initialization operation takes O(n) time Each deletion operation takes O(log n) time Thus, the total time is O(n log n) - Why? The heap has to be reinitialized (melded) after each delete operation – 67 compare with O(n 2) for sort methods of Chapter 2

Machine Scheduling Problem l l l 68 m identical machines n jobs to be performed The machine scheduling problem is to assign jobs to machines so that the time at which the last job completes is minimum

Machine Scheduling Example l l l 69 3 machines and 7 jobs job times are [6, 2, 3, 5, 10, 7, 14] What are some possible schedules? A possible schedule: What algorithm did we use for the above scheduling? What are other scheduling algorithms

Machine Scheduling Example l l l 70 What is the finish time (length) of the schedule? 21 Objective: Find schedules with minimum finish time Minimum finish time scheduling is NP-hard.

NP-hard Problems l l l 71 The class of problems for which no one has developed a polynomial time algorithm. No algorithm whose complexity is O(nk ml) is known for any NP-hard problem (for any constants k and l) NP stands for Nondeterministic Polynomial NP-hard problems are often solved by heuristics (or approximation algorithms), which do not guarantee optimal solutions Longest Processing Time (LPT) rule is a good heuristic for minimum finish time scheduling.

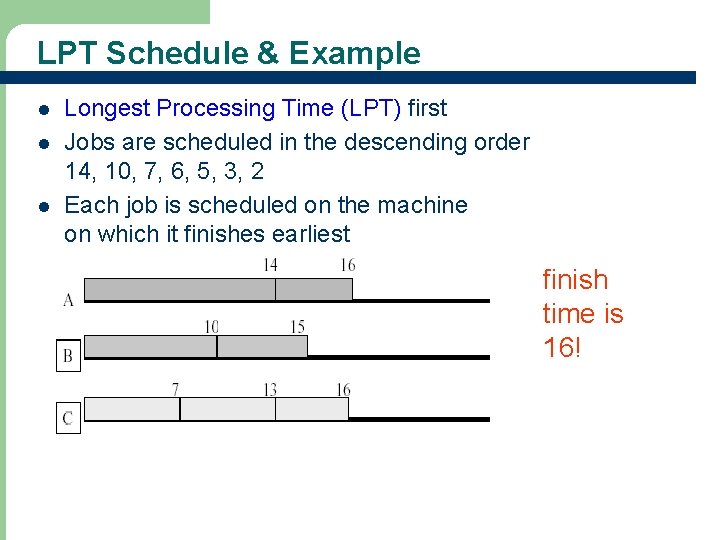
LPT Schedule & Example l l l Longest Processing Time (LPT) first Jobs are scheduled in the descending order 14, 10, 7, 6, 5, 3, 2 Each job is scheduled on the machine on which it finishes earliest finish time is 16! 72

LPT Schedule & Example l l 73 What is the minimum finish time with thee machines for jobs (2, 14, 4, 16, 6, 5, 3)? See Figure 12. 10

LPT using a Min Heap l l l 74 Min Heap has the finish times of the m machines. Initial finish times are all 0. To schedule a job, remove the machine with minimum finish time from the heap. Update the finish time of the selected machine and put the machine back into the min heap. See Program 12. 9 for LPT scheduler

Complexity Analysis of LPT l l l l 75 When n m (i. e. , more machines than jobs), LPT takes (1) time When n m, (i. e. , more jobs than machines), the heap sort takes O(n log n) time Heap initialization takes O(m) time Delete. Min operation takes O(log m) time Insert operation takes O(log m) time n Delete. Min and n Insert takes O(n log m) time Thus, the total time is O(n log n + n log m) = O(n log n) time (as n > m)

Huffman Codes l l l 76 For text compression, the LZW method relies on the recurrence of substrings in a text Huffman codes is another text compression method, which relies on the relative frequency (i. e. , the number of occurrences of a symbol) with which different symbols appear in a text Uses extended binary trees Variable-length codes that satisfy the property, where no code is a prefix of another Huffman tree is a binary tree with minimum weighted external path length for a given set of frequencies (weights)

Huffman Codes l READ Section 12. 6. 3 l READ all of Chapter 12 77