Heaps Binomial Lazy Heaps Binomial Heaps 1 Heaps

Heaps Binomial Lazy Heaps Binomial Heaps 1
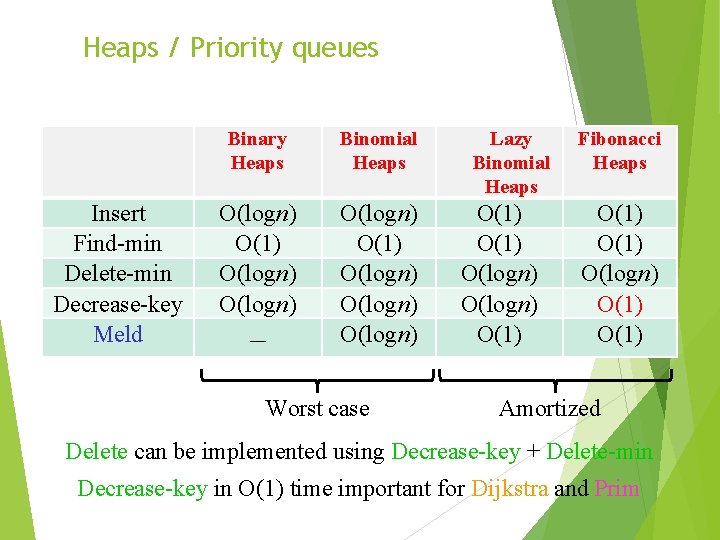
Heaps / Priority queues Insert Find-min Delete-min Decrease-key Meld Binary Heaps Binomial Heaps O(logn) O(1) O(logn) O(logn) – Worst case Lazy Binomial Heaps O(1) O(logn) O(1) Fibonacci Heaps O(1) O(logn) O(1) Amortized Delete can be implemented using Decrease-key + Delete-min Decrease-key in O(1) time important for Dijkstra and Prim

Binomial Heaps 3
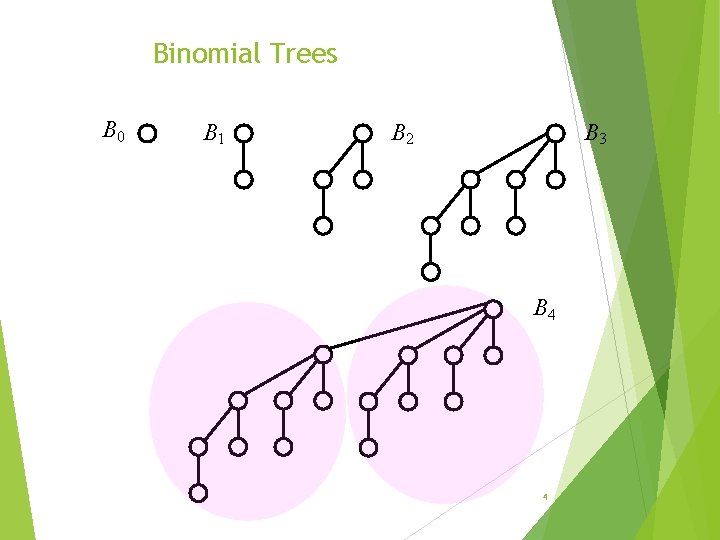
Binomial Trees B 0 B 1 B 3 B 2 B 4 4
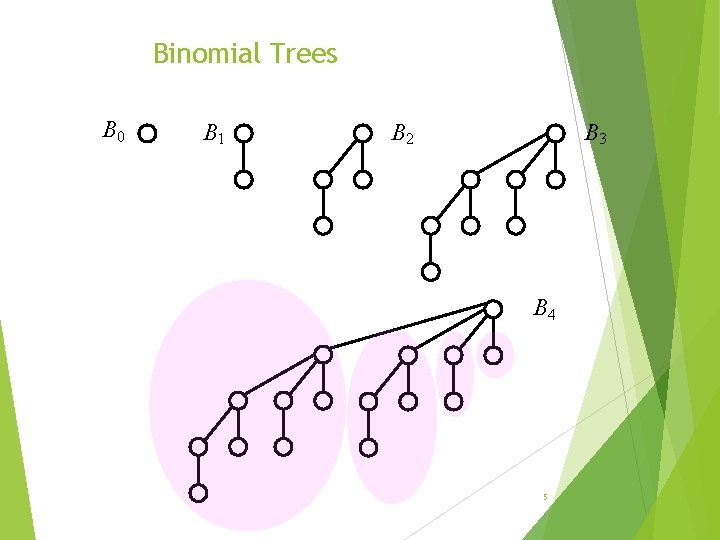
Binomial Trees B 0 B 1 B 3 B 2 B 4 5
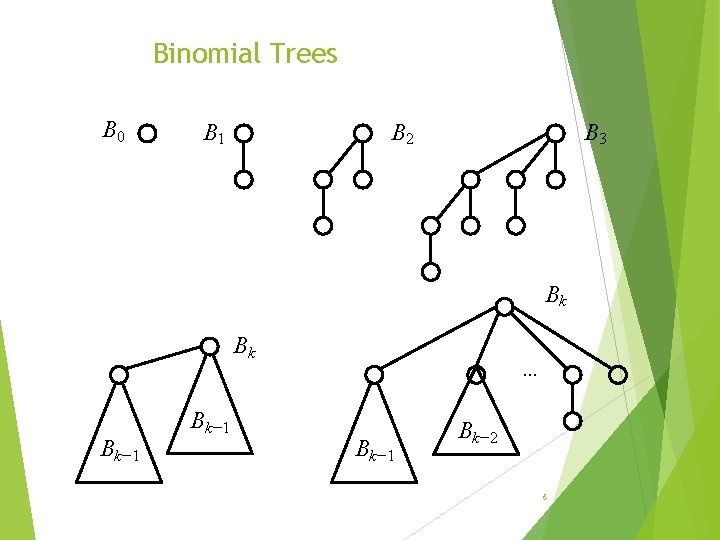
Binomial Trees B 0 B 1 B 3 B 2 Bk Bk Bk− 1 … Bk− 1 Bk− 2 6

Binomial Trees Bk Bk B 0 Bk− 1 … Bk− 1 Bk− 2 7
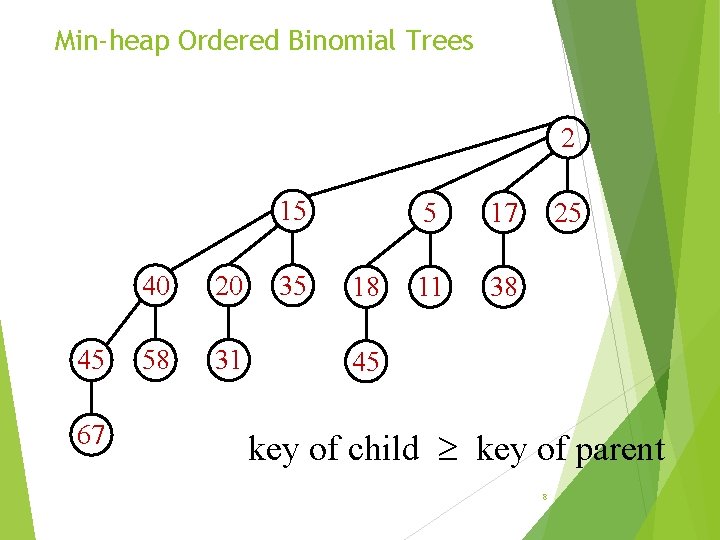
Min-heap Ordered Binomial Trees 2 15 45 67 40 20 58 31 35 18 5 17 11 38 25 45 key of child key of parent 8
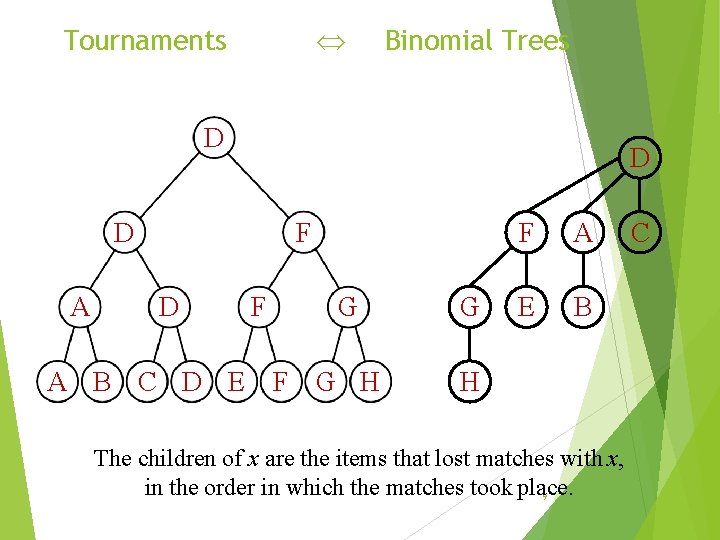
Tournaments Binomial Trees D D D A F D A B C D E F G H G F A E B H The children of x are the items that lost matches with x, in the order in which the matches took place. 9 C
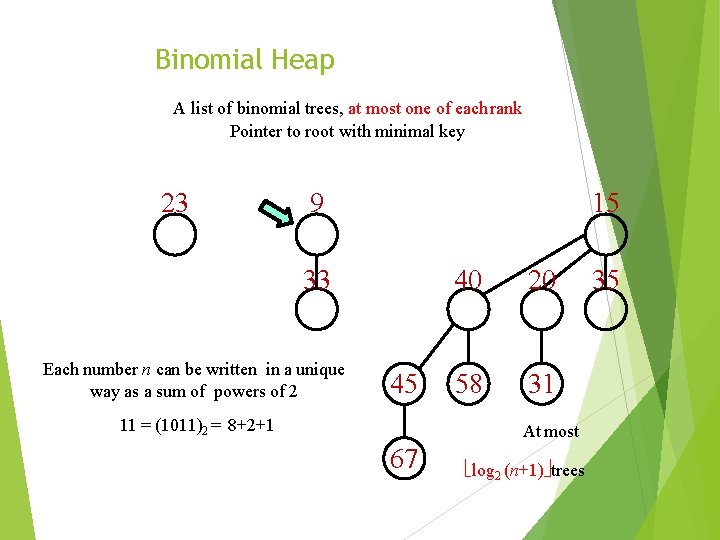
Binomial Heap A list of binomial trees, at most one of each rank Pointer to root with minimal key 23 9 15 33 Each number n can be written in a unique way as a sum of powers of 2 45 11 = (1011)2 = 8+2+1 40 20 58 31 At most 67 log 2 (n+1) trees 35
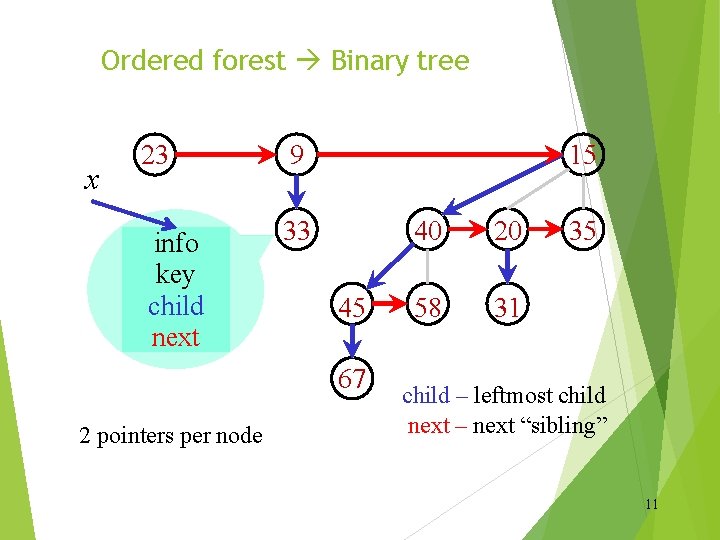
Ordered forest Binary tree x 23 9 info key child next 33 15 45 67 2 pointers per node 40 20 58 31 35 child – leftmost child next – next “sibling” 11
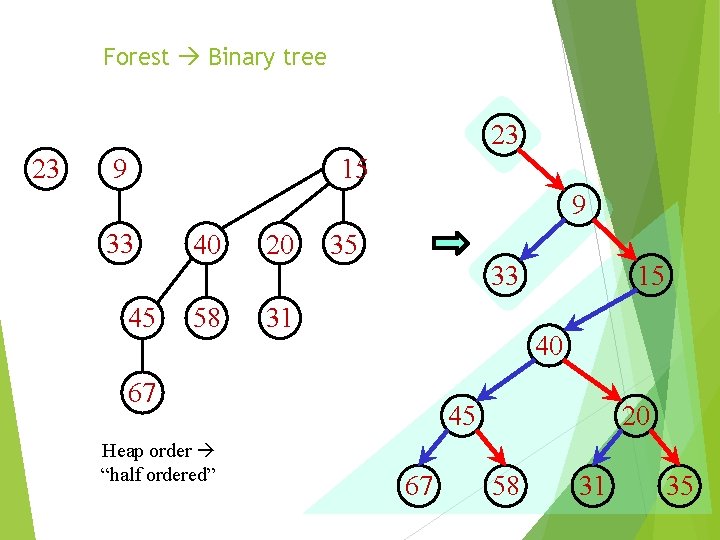
Forest Binary tree 23 23 15 9 9 33 45 40 20 58 31 35 33 40 67 Heap order “half ordered” 15 45 67 20 58 31 35
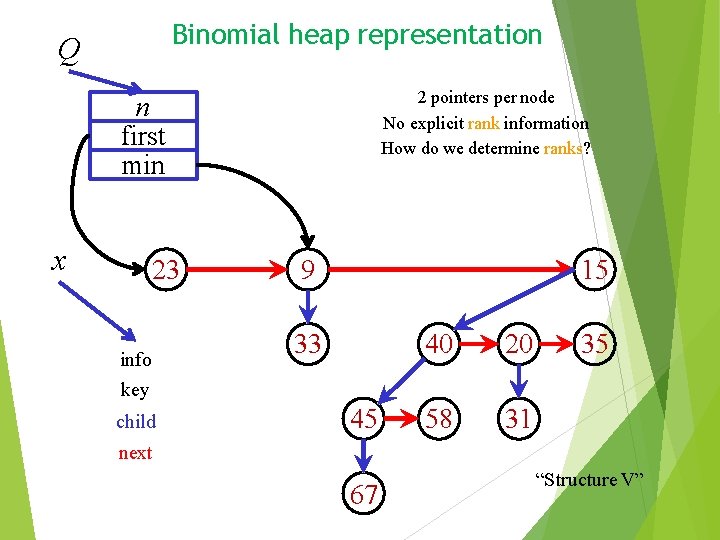
Binomial heap representation Q 2 pointers per node No explicit rank information How do we determine ranks? n first min x 23 info 9 15 33 40 20 58 31 35 key child 45 next 67 “Structure V”
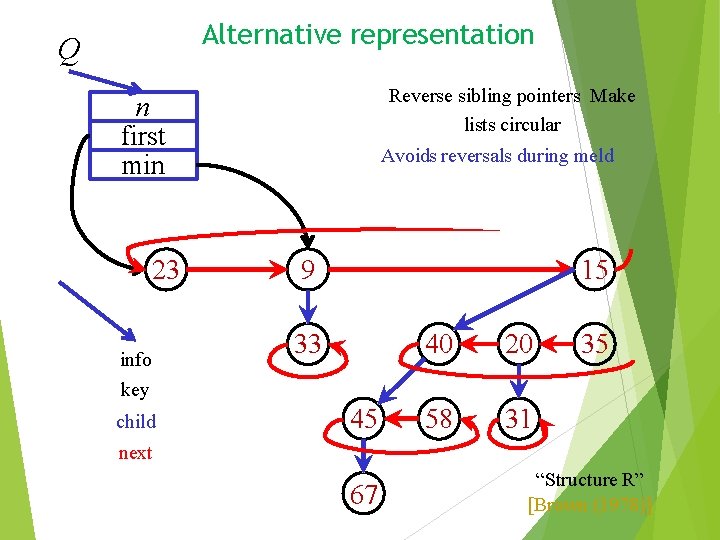
Alternative representation Q Reverse sibling pointers Make lists circular n first min 23 info Avoids reversals during meld 9 15 33 40 20 58 31 35 key child 45 next 67 “Structure R” [Brown (1978)]
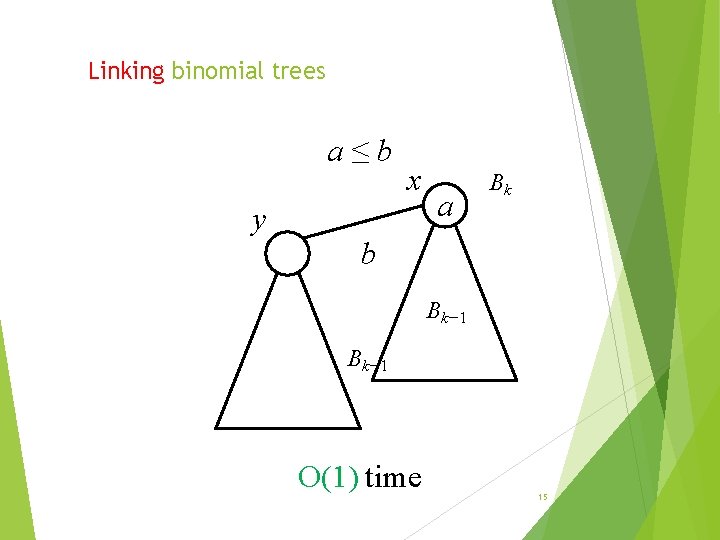
Linking binomial trees a≤b y x a Bk b Bk− 1 O(1) time 15
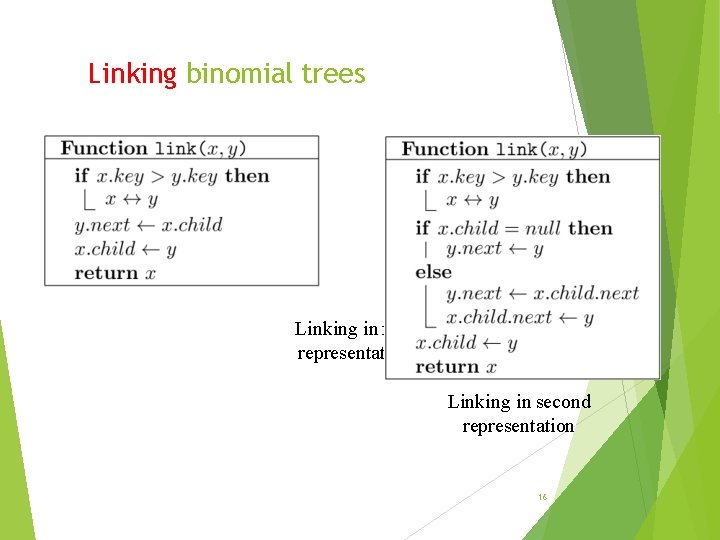
Linking binomial trees Linking in first representation Linking in second representation 16
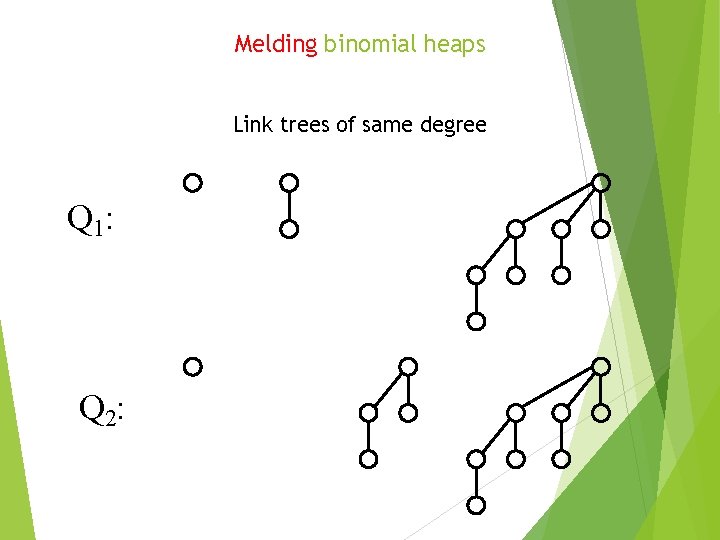
Melding binomial heaps Link trees of same degree Q 1: Q 2:
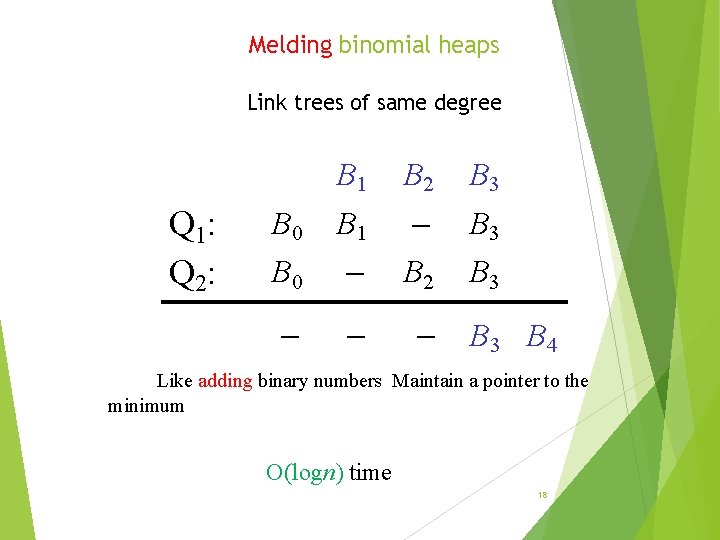
Melding binomial heaps Link trees of same degree Q 1: Q 2: B 1 B 2 B 3 B 0 B 1 B 3 B 0 B 2 B 3 B 4 Like adding binary numbers Maintain a pointer to the minimum O(logn) time 18
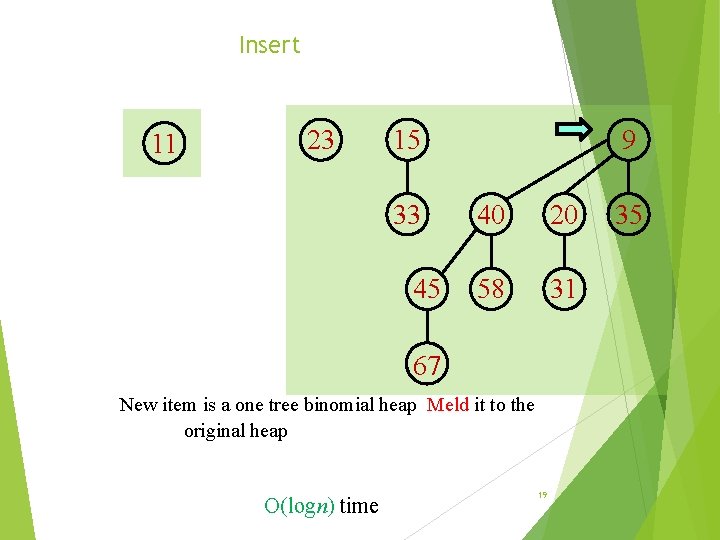
Insert 11 23 15 33 45 9 40 20 58 31 67 New item is a one tree binomial heap Meld it to the original heap O(logn) time 19 35
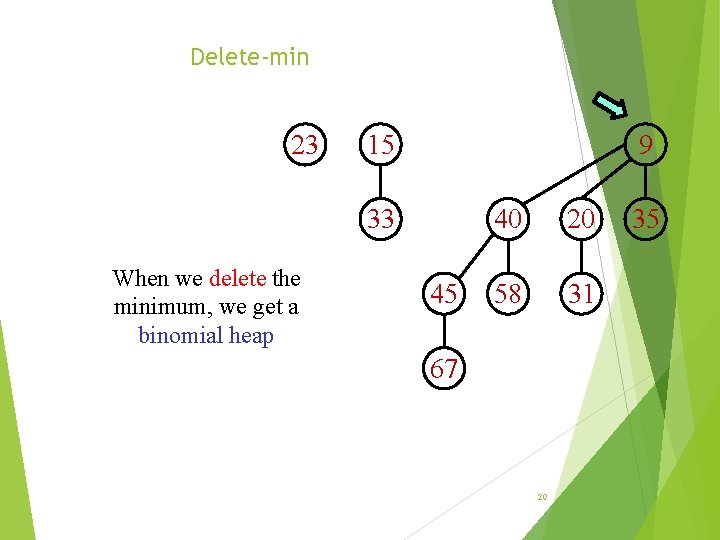
Delete-min 23 15 9 33 When we delete the minimum, we get a binomial heap 45 40 20 58 31 67 20 35
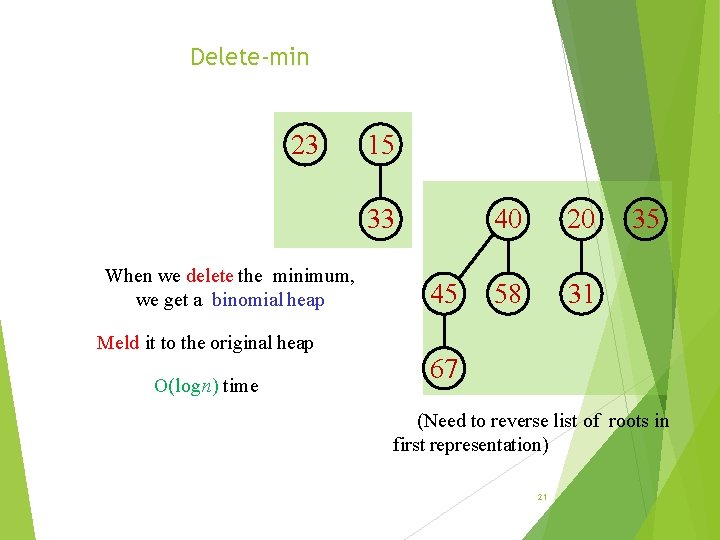
Delete-min 23 15 33 When we delete the minimum, we get a binomial heap Meld it to the original heap O(logn) time 45 40 20 58 31 35 67 (Need to reverse list of roots in first representation) 21
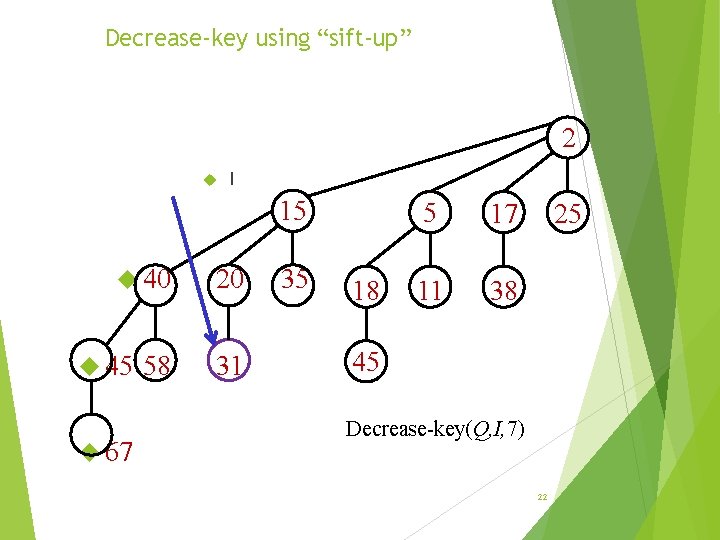
Decrease-key using “sift-up” 2 I 15 40 45 67 58 20 31 35 18 5 17 11 38 25 45 Decrease-key(Q, I, 7) 22
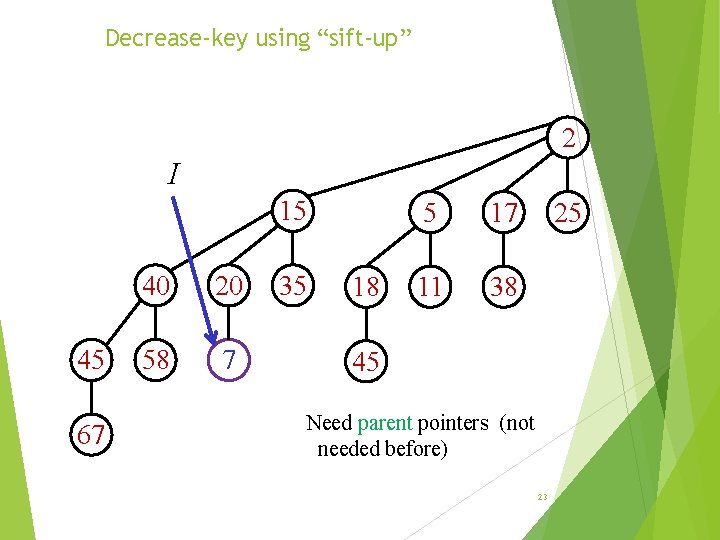
Decrease-key using “sift-up” 2 I 15 45 67 40 20 58 7 35 18 5 17 11 38 25 45 Need parent pointers (not needed before) 23
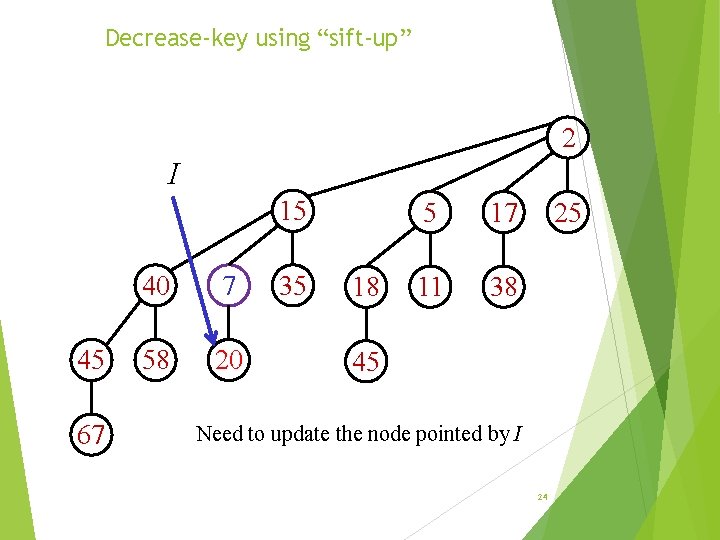
Decrease-key using “sift-up” 2 I 15 45 67 40 7 58 20 35 18 5 17 11 38 25 45 Need to update the node pointed by I 24
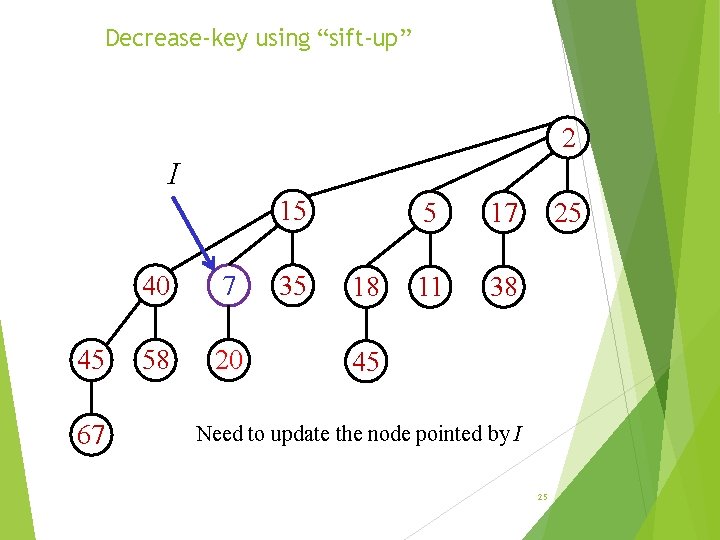
Decrease-key using “sift-up” 2 I 15 45 67 40 7 58 20 35 18 5 17 11 38 25 45 Need to update the node pointed by I 25
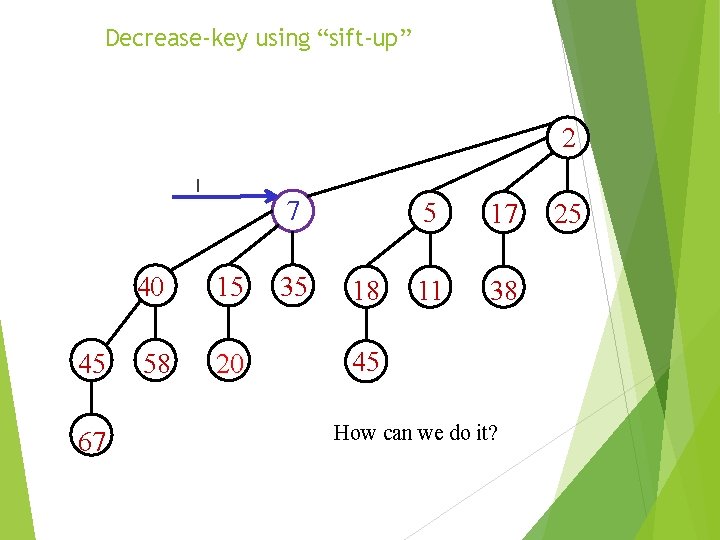
Decrease-key using “sift-up” 2 I 45 67 7 40 15 58 20 35 18 5 17 11 38 45 How can we do it? 25
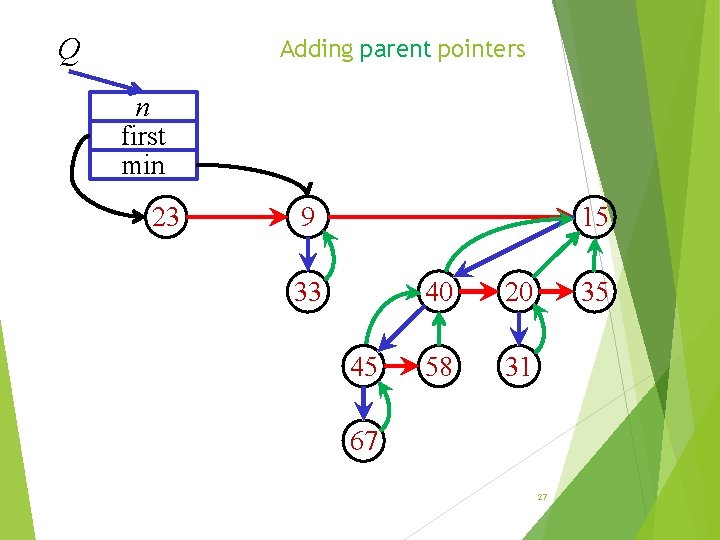
Q Adding parent pointers n first min 23 9 15 33 45 40 20 58 31 35 67 27
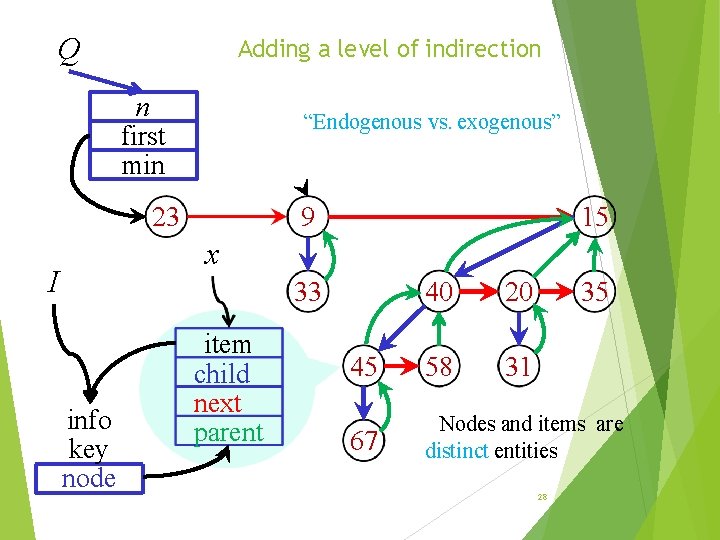
Q Adding a level of indirection n first min “Endogenous vs. exogenous” 23 9 15 x I 33 info key node item child next parent 40 20 35 45 58 31 67 Nodes and items are distinct entities 28
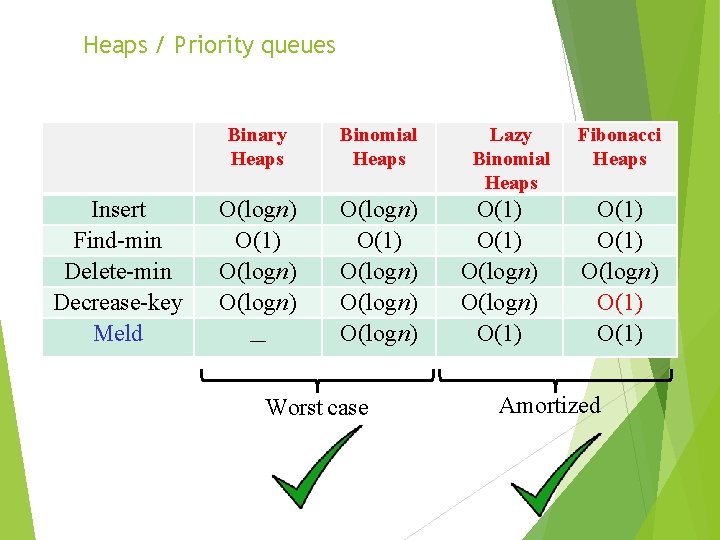
Heaps / Priority queues Insert Find-min Delete-min Decrease-key Meld Binary Heaps Binomial Heaps O(logn) O(1) O(logn) O(logn) – Worst case Lazy Binomial Heaps O(1) O(logn) O(1) Fibonacci Heaps O(1) O(logn) O(1) Amortized

Lazy Binomial Heaps 30

Binomial Heaps A list of binomial trees, at most one of each rank, sorted by rank (at most O(logn) trees) Pointer to root with minimal key Lazy Binomial Heaps An arbitrary list of binomial trees (possibly n trees of size 1) Pointer to root with minimal key
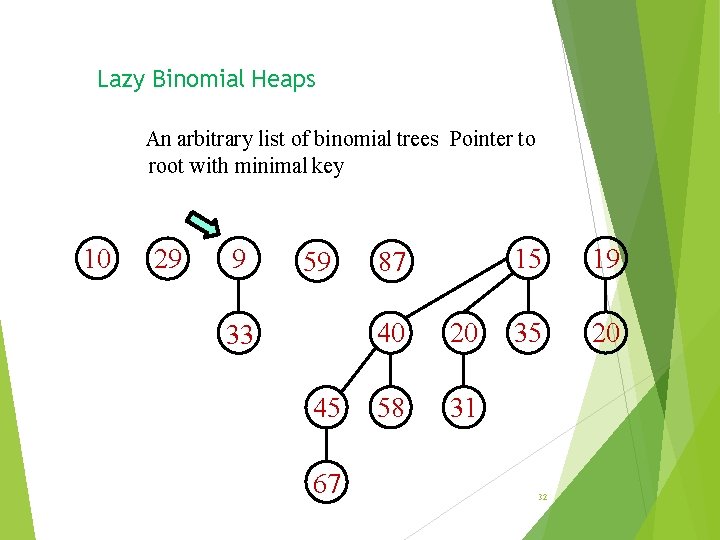
Lazy Binomial Heaps An arbitrary list of binomial trees Pointer to root with minimal key 10 29 9 59 33 45 67 87 40 20 58 31 15 19 35 20 32

Lazy Meld Concatenate the two lists of trees Update the pointer to root with minimal key O(1) worst case time Lazy Insert Add the new item to the list of roots Update the pointer to root with minimal key O(1) worst case time 33
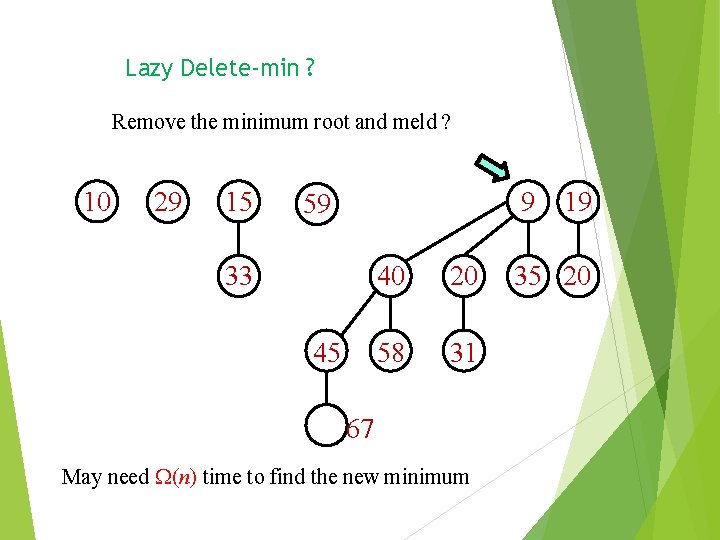
Lazy Delete-min ? Remove the minimum root and meld ? 10 29 15 9 59 33 45 40 20 58 31 67 May need (n) time to find the new minimum 19 35 20
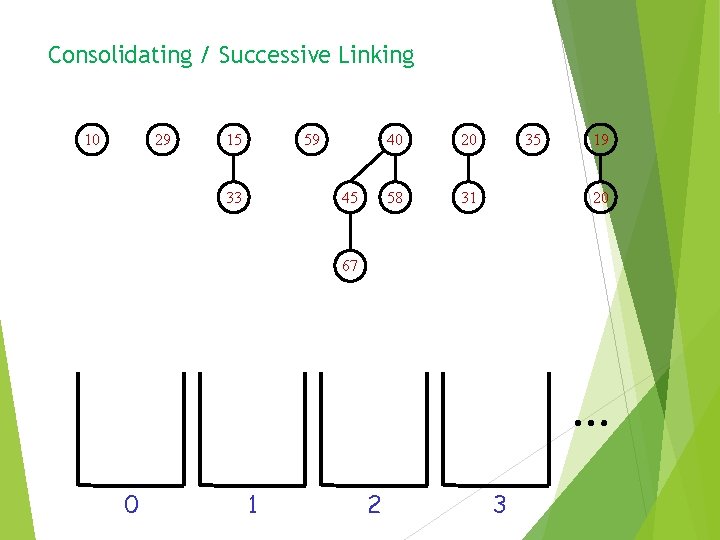
Consolidating / Successive Linking 10 29 15 59 33 45 40 20 58 31 35 19 20 67 … 0 1 2 3
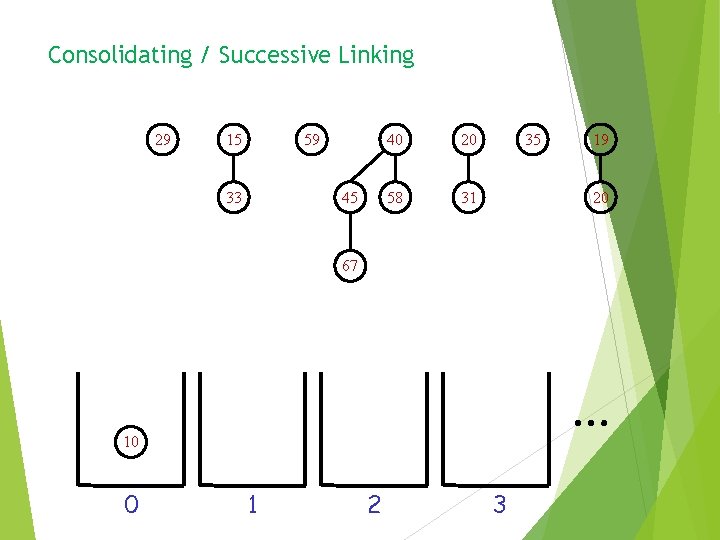
Consolidating / Successive Linking 29 15 59 33 45 40 20 58 31 35 19 20 67 … 10 0 1 2 3
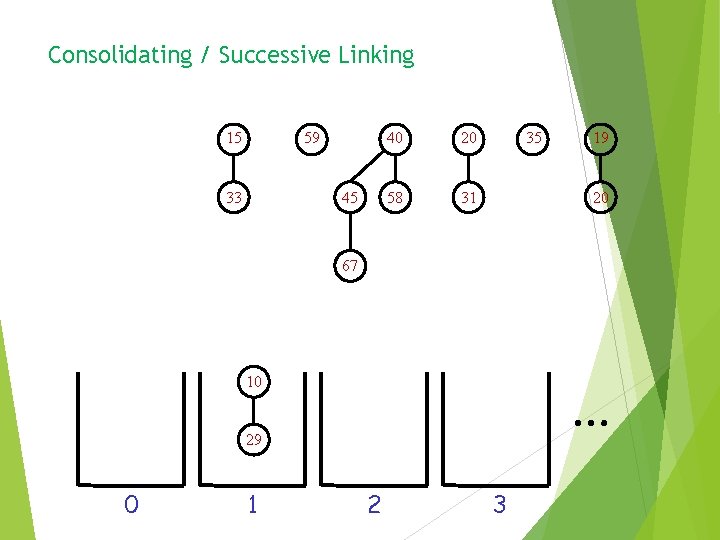
Consolidating / Successive Linking 15 59 33 45 40 20 58 31 35 19 20 67 … 10 29 0 1 2 3
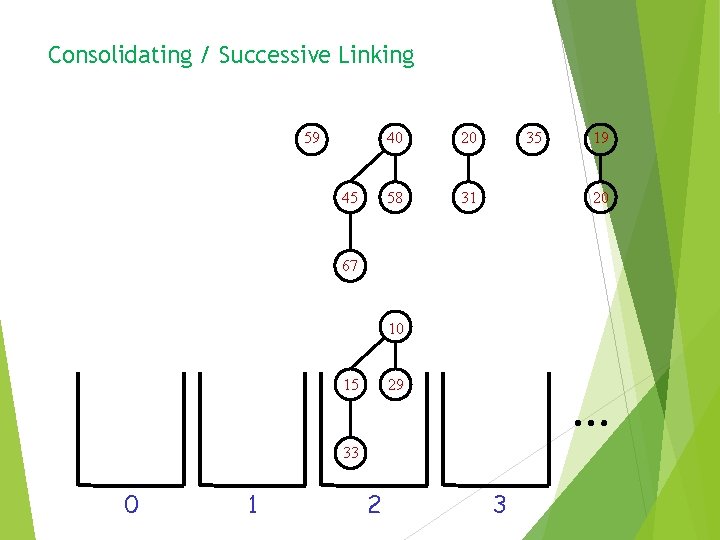
Consolidating / Successive Linking 59 45 40 20 58 31 35 19 20 67 10 15 … 29 33 0 1 2 3
Consolidating / Successive Linking 45 40 20 58 31 35 19 20 67 10 15 … 29 59 33 0 1 2 3
Consolidating / Successive Linking 20 35 19 31 20 10 45 59 0 40 15 58 33 67 1 2 3 29 …
Consolidating / Successive Linking 35 19 20 10 20 59 0 45 15 58 33 67 31 1 40 2 3 29 …
Consolidating / Successive Linking 19 20 35 10 59 20 45 1 15 58 33 67 31 0 40 2 3 29 …
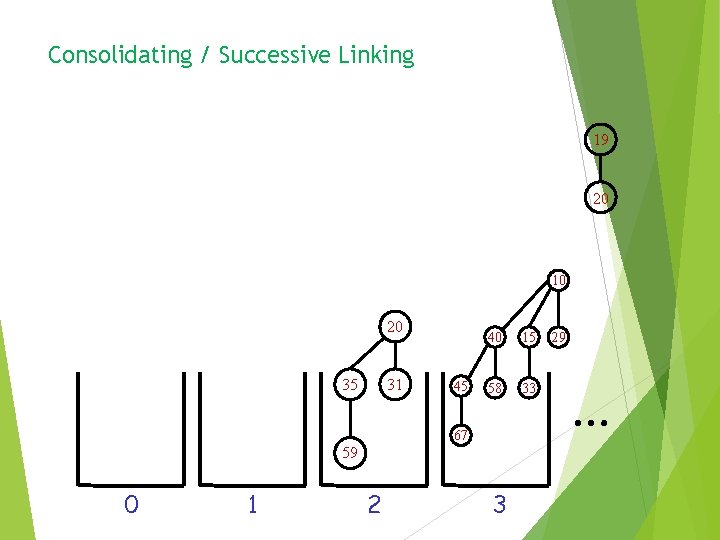
Consolidating / Successive Linking 19 20 10 20 35 31 45 40 15 58 33 67 59 0 1 2 3 29 …
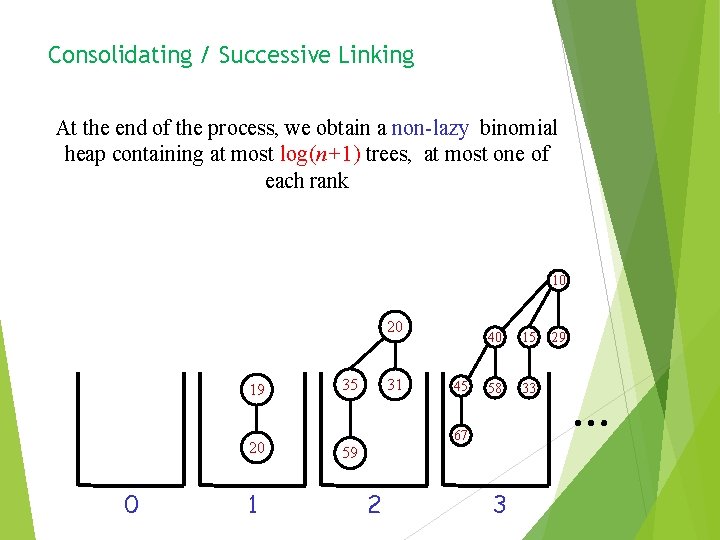
Consolidating / Successive Linking At the end of the process, we obtain a non-lazy binomial heap containing at most log(n+1) trees, at most one of each rank 10 20 19 20 0 1 35 31 45 40 15 58 33 67 59 2 3 29 …

Outline q Lazy Union q Extract-Min q Analysis

Amortized Thinking Union violates binomial heaps structural property Let the Extract-Min convert the lazy version back to a clean binomial heap Extract-Min can cost ϴ( n ) in worst-case However, it is O( log n ) amortized time ! Union : increase potential Extract-Min : decrease potential

Extract-Min : Amortized Analysis • Let Ti be the number of trees after the ith operation r be the rank of the tree containing the min. • Extract-Min actual cost –ϴ( # trees ) = ϴ( r + Ti-1 ) = O( log n + Ti-1) –r = O( log n ) since all the trees are binomial trees

Extract-Min : Amortized Analysis Let the potential function Фi = Ti ai = ci + Фi - Фi-1 = O( log n + Ti-1) + (Ti - Ti-1) = O( log n + Ti-1) + O( log n ) - Ti-1 = O( log n ) + O( Ti-1) - Ti-1 = O( log n )

Potential Energy H Ф
Potential Energy H Ф Lazy Binomial Heap - Insert
Potential Energy H Ф Lazy Binomial Heap – Extract-Min
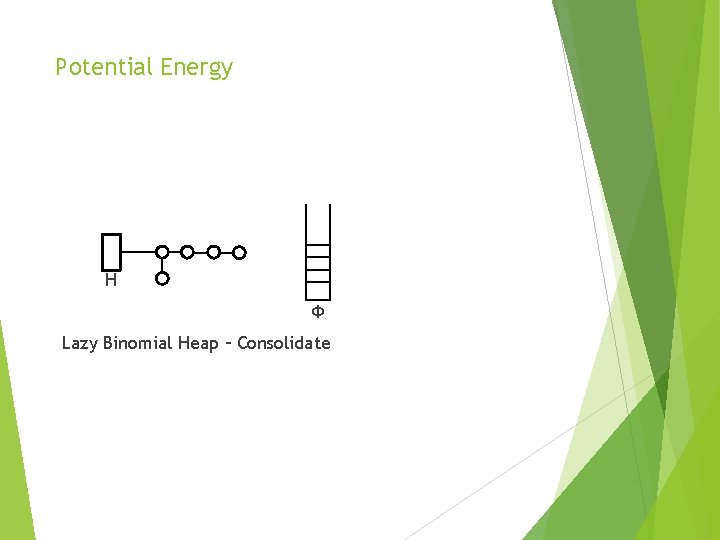
Potential Energy H Ф Lazy Binomial Heap – Consolidate
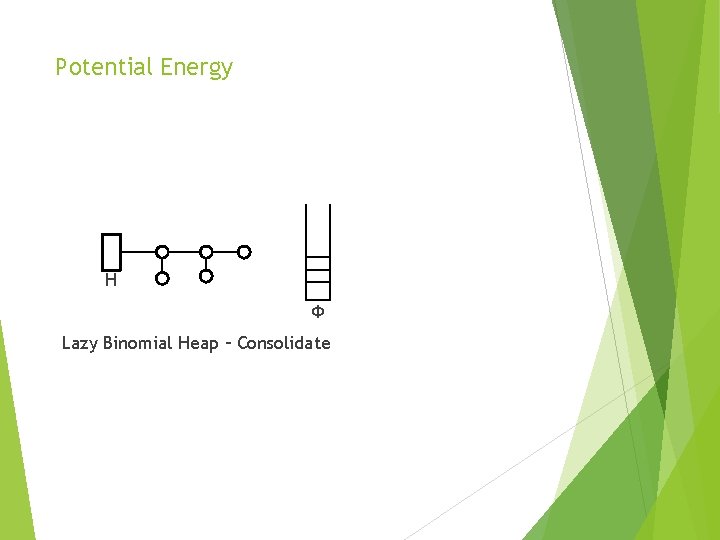
Potential Energy H Ф Lazy Binomial Heap – Consolidate
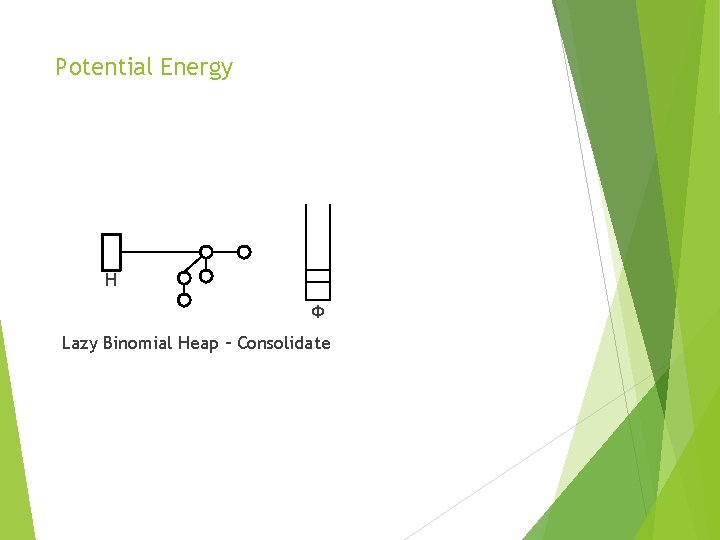
Potential Energy H Ф Lazy Binomial Heap – Consolidate

Accounting Method Invarient : one baht credited at each root node for future consolidating task. H
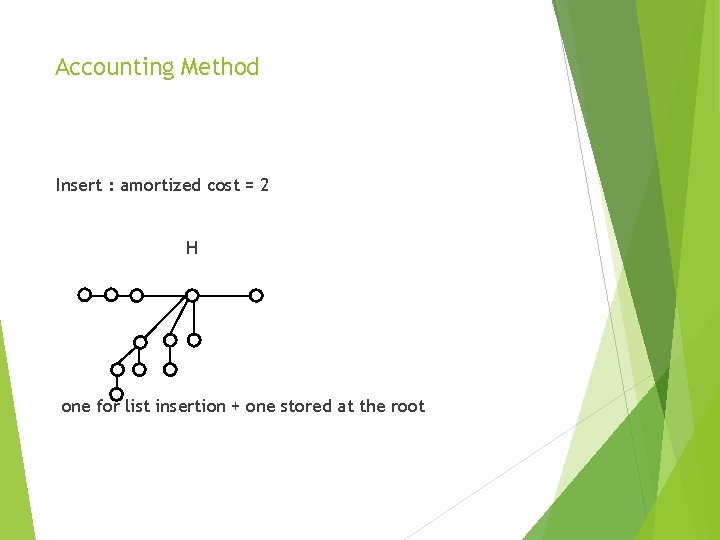
Accounting Method Insert : amortized cost = 2 H one for list insertion + one stored at the root

Accounting Method Extract-Min : amortized cost = O( log n ) H

Accounting Method Extract-Min : amortized cost = O( log n ) H
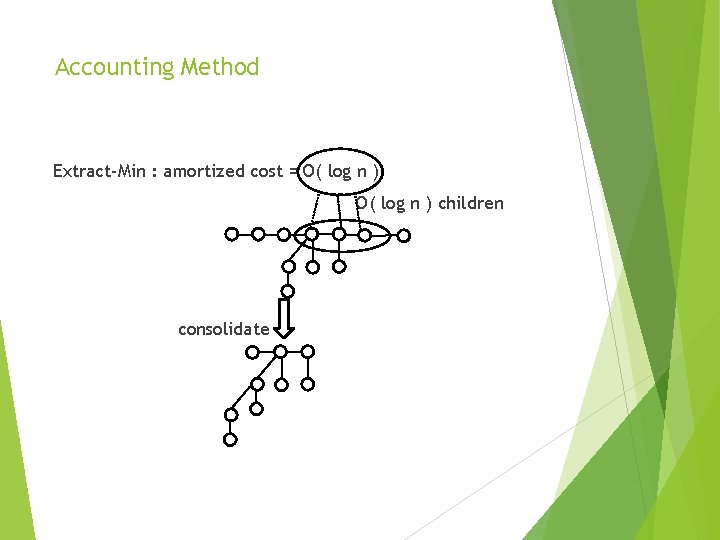
Accounting Method Extract-Min : amortized cost = O( log n ) children consolidate

Cost of Consolidating T 0 – Number of trees before T 1 – Number of trees after L – Number of links T 1 = T 0−L (Each link reduces the number of tree by 1) Total number of trees processed – T 0+L (Each link creates a new tree) Putting trees into buckets or finding trees to link with Linking Handling the buckets Total cost = O( (T 0+L) + L + log 2 n ) = O( T 0+ log 2 n ) As L ≤ T 0

Amortized Cost of Consolidating (Scaled) actual cost = T 0 + log 2 n Change in potential = = T 1−T 0 Amortized cost = (T 0 + log 2 n ) + (T 1−T 0) = T 1 + log 2 n ≤ 2 log 2 n As T 1 ≤ log 2 n Another view: A link decreases the potential by 1. This can pay for handling all the trees involved in the link. The only “unaccounted” trees are those that were not the input nor the output of a link operation.

Consolidating / Successive Linking At the end of the process, we obtain a non-lazy binomial heap containing at most logn trees, at most one of each degree Worst case cost – O(n) Amortized cost – O(logn) Potential = Number of Trees
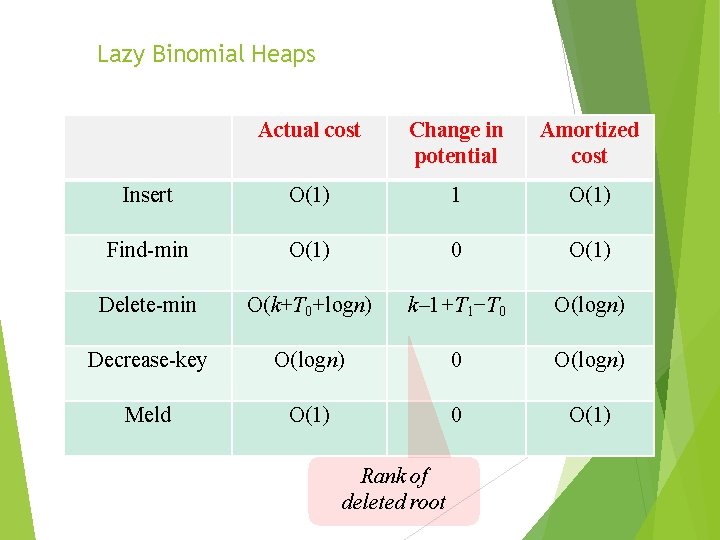
Lazy Binomial Heaps Actual cost Change in potential Amortized cost Insert O(1) 1 O(1) Find-min O(1) 0 O(1) Delete-min O(k+T 0+logn) k 1+T 1−T 0 O(logn) Decrease-key O(logn) 0 O(logn) Meld O(1) 0 O(1) Rank of deleted root
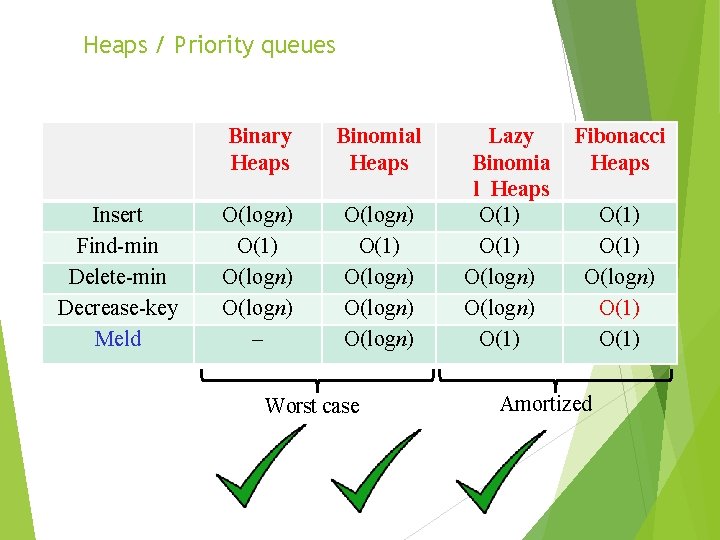
Heaps / Priority queues Insert Find-min Delete-min Decrease-key Meld Binary Heaps Binomial Heaps O(logn) O(1) O(logn) – O(logn) O(1) O(logn) Worst case Lazy Binomia l Heaps O(1) O(logn) O(1) Fibonacci Heaps O(1) O(logn) O(1) Amortized

Heaps / Priority queues Lazy binomial heap - amortized cost Union : increase potential : ϴ (1) Insert : increase potential : ϴ (1) Extract-Min : decrease potential : O( log n ) Decrease-Key, Delete : ϴ ( log n )

Properties of binomial trees 1) | Bk | = 2 k 2) degree(root(Bk)) 3) depth(Bk) = = k k ==> The degree and depth of a binomial tree with at most n nodes is at most log(n). Define the rank of Bk to be k 66
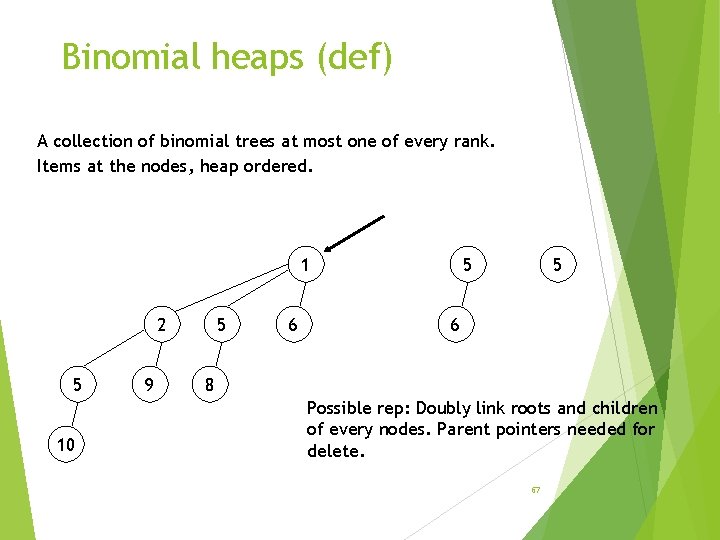
Binomial heaps (def) A collection of binomial trees at most one of every rank. Items at the nodes, heap ordered. 1 2 5 10 9 5 6 5 5 6 8 Possible rep: Doubly link roots and children of every nodes. Parent pointers needed for delete. 67
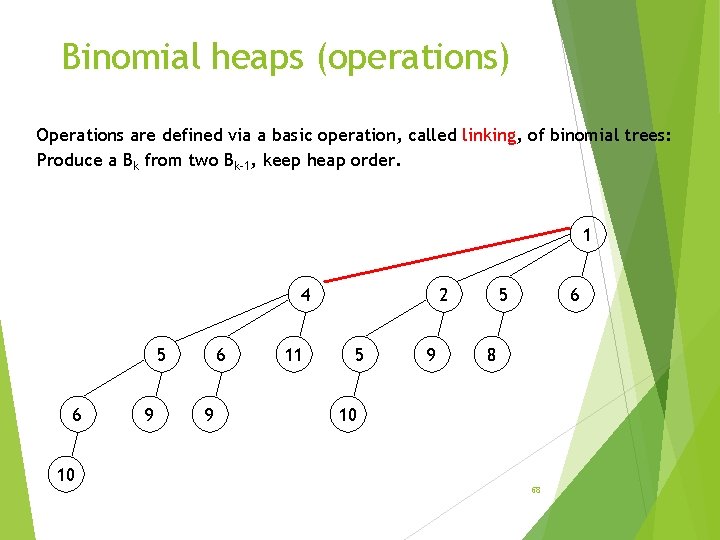
Binomial heaps (operations) Operations are defined via a basic operation, called linking, of binomial trees: Produce a Bk from two Bk-1, keep heap order. 1 4 5 6 9 11 2 5 9 5 6 8 10 10 68

Binomial heaps (ops cont. ) Basic operation is meld(h 1, h 2): Like addition of binary numbers. B 5 B 4 B 2 h 1: B 4 B 3 h 2: B 4 B 3 B 5 B 4 B 1 B 0 B 2 69 +

Binomial heaps (ops cont. ) Findmin(h): obvious Insert(x, h) : meld a new heap with a single B 0 containing x, with h deletemin(h) : Chop off the minimal root. Meld the subtrees with h. Update minimum pointer if needed. delete(x, h) : Bubble up and continue like delete-min decrease-key(x, h, ) : Bubble up, update min ptr if needed All operations take O(log n) time on the worst case, except find-min(h) that takes O(1) time. 70

Amortized analysis We are interested in the worst case running time of a sequence of operations. Example: binary counter single operation -- increment 000001 00010 00011 00100 00101 71

Amortized analysis (Cont. ) On the worst case increment takes O(k). k = #digits What is the complexity of a sequence of increments (on the worst case) ? Define a potential of the counter: (c) = ? Amortized(increment) = actual(increment) + 72

Amortized analysis (Cont. ) Amortized(increment 1) = actual(increment 1) + 1 - 0 Amortized(increment 2) = actual(increment 2) + 2 - 1 + … … Amortized(incrementn) = actual(incrementn) + n- (n-1) i. Amortized(incrementi) = iactual(incrementi) + n- 0 i. Amortized(incrementi) iactual(incrementi) if n- 0 0 73

Amortized analysis (Cont. ) Define a potential of the counter: (c) = #(ones) Amortized(increment) = actual(increment) + Amortized(increment) = 1+ #(1 => 0) + 1 - #(1 => 0) = O(1) ==> Sequence of n increments takes O(n) time 74

Binomial heaps - amortized ana. (collection of heaps) = #(trees) Amortized cost of insert O(1) Amortized cost of other operations still O(log n) 75

Binomial heaps + lazy meld Allow more than one tree of each rank. Meld (h 1, h 2) : • Concatenate the lists of binomial trees. • Update the minimum pointer to be the smaller of the minimums O(1) worst case and amortized. 76

Binomial heaps + lazy meld As long as we do not do a delete-min our heaps are just doubly linked lists: 9 5 9 11 4 6 Delete-min : Chop off the minimum root, add its children to the list of trees. Successive linking: Traverse the forest keep linking trees of the same rank, maintain a pointer to the minimum root. 77

Binomial heaps + lazy meld Possible implementation of delete-min is using an array indexed by rank to keep at most one binomial tree of each rank that we already traversed. Once we encounter a second tree of some rank we link them and keep linking until we do not have two trees of the same rank. We record the resulting tree in the array Amortized(delete-min) = = (#(trees at the end) + #links + max-rank) - #links (2 log(n) + #links) - #links = O(log(n)) 78

Binomial heaps + lazy delete Allow more than one tree of each rank. Meld (h 1, h 2), Insert(x, h) -- as before Delete(x, h) : simply mark x as deleted. Deletemin(h) : y = findmin(h) ; delete(y, h) How do we do findmin ? 79

Binomial heaps + lazy delete Traverse the trees top down purging deleted nodes and stopping at each non-deleted node Do successive linking on the forest you obtain. 80
Binomial heaps + lazy delete 81
Binomial heaps + lazy delete 82

Binomial heaps + lazy delete (ana. ) Modify the potential a little: (collection of heaps) = #(trees) + #(deleted nodes) Insert, meld, delete : O(1) delete-min : like find-min What is the amortized cost of find-min ? 83

Binomial heaps + lazy delete (ana. ) What is the amortized cost of find-min ? amortized(find-min) = amortized(purging) + amortized(successive linking + scan of undeleted nodes) We saw that: amortized(successive linking) = O(log(n)) Amortized(purge) = actual(purge) + (purge) Actual(purge) = #(nodes purged) + #(new trees) (purge) = #(new trees) - #(nodes purged) So, amortized(find-min) = O(log(n) + #(new trees) ) 84

Binomial heaps + lazy delete (ana. ) How many new trees are created by the purging step ? Let p = #(nodes purged), n = total #(nodes) Then #(new trees) = O( p*(log(n/p)+ 1) ) So, amortized(find-min) = O( p*(log(n/p)+ 1) ) Proof. Suppose the i-th purged node, 1 i p, had ki undeleted children. One of them has degree at least ki-1. Therefore in its subtree there at least 2(ki-1) nodes. 85

Binomial heaps + lazy delete (ana. ) Proof (cont). How large can k 1+k 2+. . . +kp be such that i=1 2(ki-1) p n ? Make all ki equal log(n/p) + 1, then i ki = p*(log(n/p)+ 1) 86

Application: The round robin algorithm of Cheriton and Tarjan (76) for MST We shall use a Union-Find data structure. The union find problem is where we want to maintain a collection of disjoint sets under the operations 1) S=Union(S 1, S 2) 2) S=find(x) Can do it in O(1) amortized time for union and O( (k, n)) amortized time for find, where k is the # of finds, and n is the number of items (assuming k ≥ n). 87

A greedy algorithm for MST Start with a forest where each tree is a singleton. Repeat the following step until there is only one tree in the forest: Pick T F, pick a minimum cost edge e connecting a vertex of T to a vertex in T’, add e to the forest (merge T and T’ to one tree) Prim’s algorithm: picks always the same T Kruskal’s algorithm: picks the lightest edge out of F 88
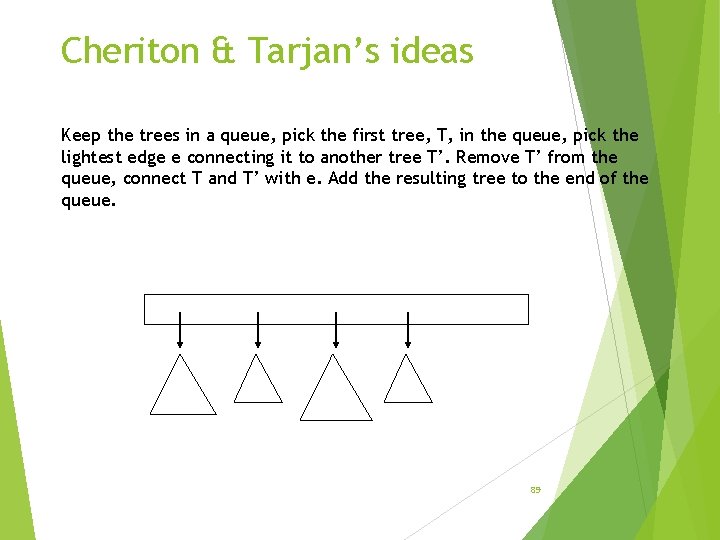
Cheriton & Tarjan’s ideas Keep the trees in a queue, pick the first tree, T, in the queue, pick the lightest edge e connecting it to another tree T’. Remove T’ from the queue, connect T and T’ with e. Add the resulting tree to the end of the queue. 89
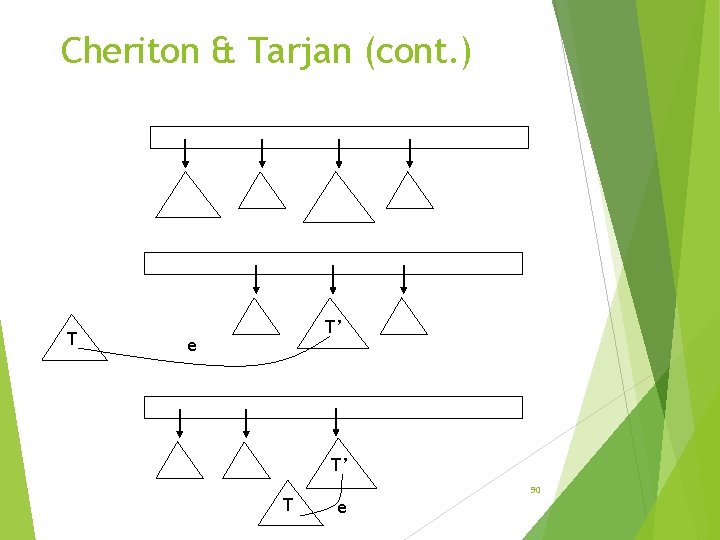
Cheriton & Tarjan (cont. ) T T’ e T’ T 90 e

Cheriton & Tarjan (implementation) The vertices of each tree T will be a set in a Union-Find data structure. Denote it also by T Edges with one endpoint in T are stored in a heap data structure. Denoted by h(T). We use binomial queues with lazy meld and deletion. Find e by doing find-min on h(T). Let e=(v, w). Find T’ by doing find(w). Then create the new tree by T’’= union(T, T’) and h(T’’) = meld(h(T), h(T’)) 91

Cheriton & Tarjan (implementation) Note: The meld implicitly delete edges. Every edge in h(T) with both endpoints in T is considered as “marked deleted”. We never explicitly delete edges! We can determine whether an edge is deleted or not by two find operations. 92

Cheriton & Tarjan (analysis) Assume for the moment that find costs O(1) time. Then we can determine whether a node is marked deleted in O(1) time, and our analysis is still valid. So, we have • at most 2 m implicit delete operations that cost O(m). • at most n find operations that cost O(n). • at most n meld and union operations that cost O(n). • at most n find-min operations. The complexity of these find-min operations dominates the complexity of the algorithm. 93

Cheriton & Tarjan (analysis) Let mi be the number of edges in the heap at the i-th iteration. Let pi be the number of deleted edges purged from the heap at the find-min performed by the i-th iteration. So, we proved that the i-th find-min costs O(pi *(log(mi / pi)+ 1) ). We want to bound the sum of these expressions. We will bound i mi first. 94

Cheriton & Tarjan (analysis) Divide the iterations into passes as follows. Pass 1 is when we remove the original singleton trees from the queue. Pass i is when we remove trees added to the queue at pass i-1. What is the size of a tree removed from the queue at pass j ? At least 2 j. (Prove by induction) So how many passes are there ? At most log(n) 95

Cheriton & Tarjan (analysis) An edge can occur in at most two heaps of trees in one pass. So i mi 2 m log(n) Recall we want to bound O( i pi *(log(mi / pi)+ 1) ). 1) Consider all find-mins such that pi mi / log 2(n): O( i pi *(log(mi / pi)+ 1) ) = O( i pi log(n)) = O(m loglog(n)) 2) Consider all find-mins such that pi mi / log 2(n): O( i pi *(log(mi / pi)+ 1) ) = O( i (mi / log 2(n)) log(mi)) = O(m) 96

Cheriton & Tarjan (analysis) We obtained a time bound of O(m loglog(n)) under the assumption that find takes O(1) time. But if you amortize the cost of the finds on O(m loglog(n)) operations then the cost per find is really (m loglog(n), n) = O(1) 97

One-pass successive linking A tree produced by a link is immediately put in the output list and not linked again Worst case cost – O(n) Amortized cost – O(logn) Potential = Number of Trees Exercise: Prove it!
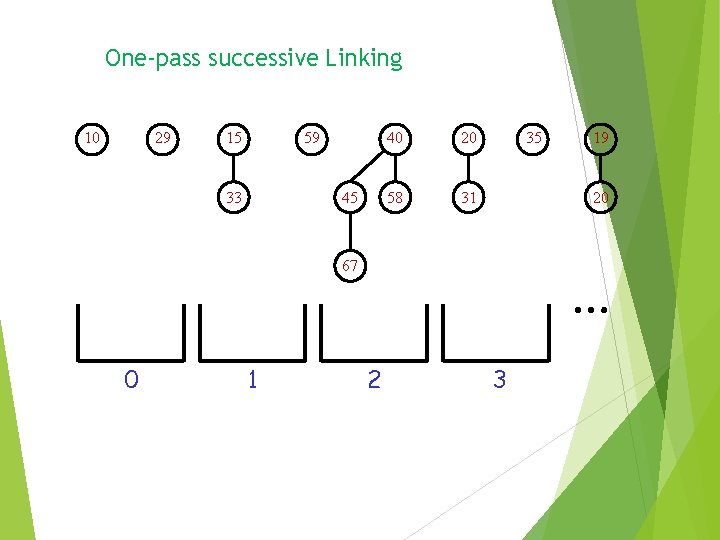
One-pass successive Linking 10 29 15 59 33 45 40 20 58 31 35 20 … 67 0 1 19 2 3
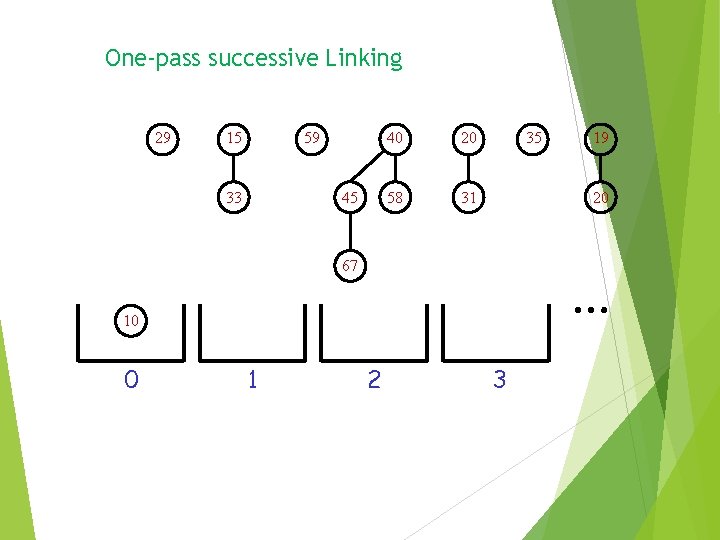
One-pass successive Linking 29 15 59 33 45 40 20 58 31 35 20 … 67 10 0 1 19 2 3
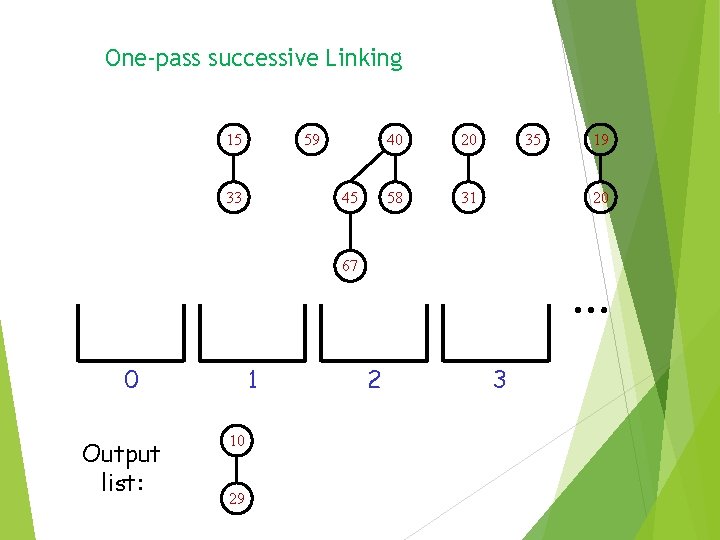
One-pass successive Linking 15 59 33 45 40 20 58 31 35 20 … 67 0 Output list: 1 10 29 19 2 3
- Slides: 101