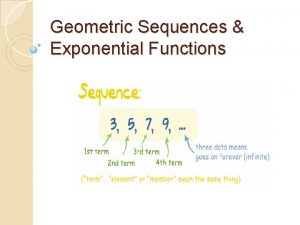
Geometric Sequence A geometric sequence is one where

Geometric Sequence A geometric sequence is one where to get from one term to the next you multiply by the same number each time. This number is called the common ratio, r. Eg 1 2 3 4 2, 10, 50, 250. . . x 5 10=5 2 x 5 50=5 10 250=5 50 r=5

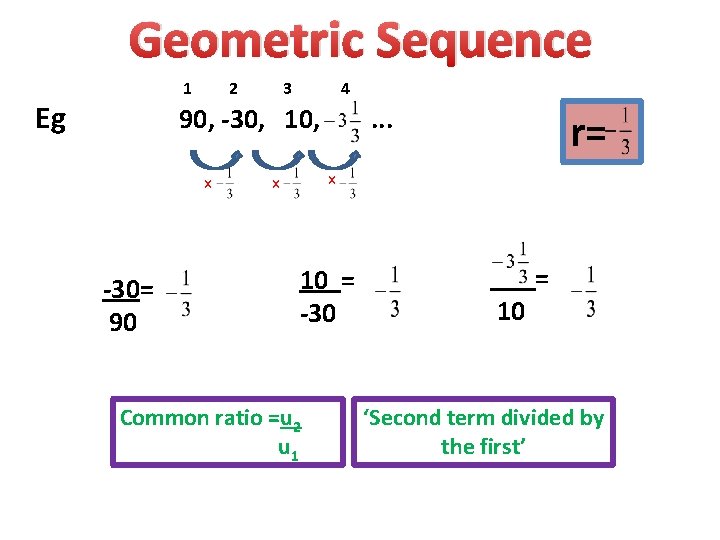
Geometric Sequence 1 Eg 2 3 4 90, -30, 10, x -30= 90 . . . r= x x 10 = -30 Common ratio =u 2 u 1 10 = ‘Second term divided by the first’

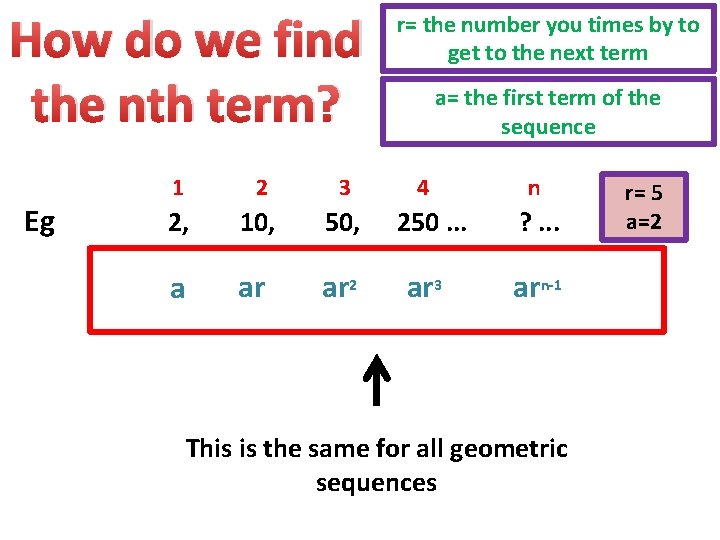
How do we find the nth term? Eg r= the number you times by to get to the next term a= the first term of the sequence 1 2 3 4 n 2, 10, 50, 250. . . ? . . . a ar ar 2 ar 3 arn-1 This is the same for all geometric sequences r= 5 a=2

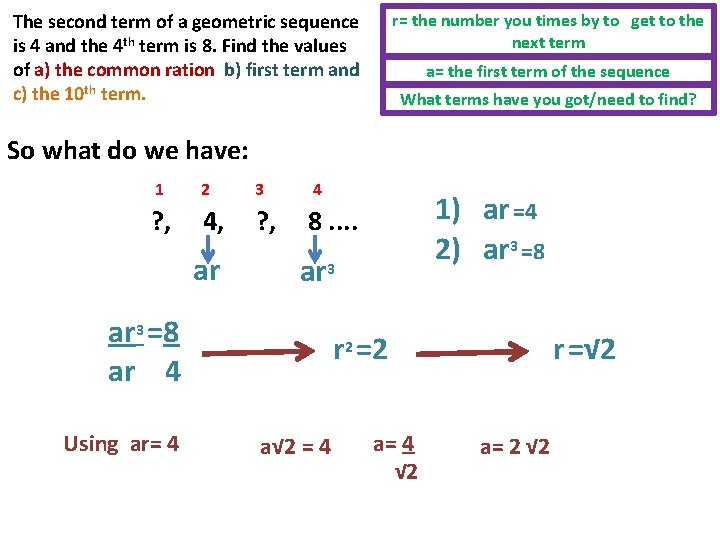
Your check list You will need to find or use these: r= the number you times by to get to the next term a= the first term of the sequence What terms have you got/need to find? The second term of a geometric sequence is 4 and the 4 th term is 8. Find the values of a) the common ration b) first term and c) the 10 th term. So what do we have: 1 2 3 4 ? , 4, ? , 8. . ar ar 3

The second term of a geometric sequence is 4 and the 4 th term is 8. Find the values of a) the common ration b) first term and c) the 10 th term. r= the number you times by to get to the next term a= the first term of the sequence What terms have you got/need to find? So what do we have: 1 2 3 4 ? , 4, ? , 8. . ar ar 3 =8 ar 4 Using ar= 4 1) ar =4 2) ar 3 =8 r 2 =2 a√ 2 = 4 a= 4 √ 2 r =√ 2 a= 2 √ 2

r =√ 2 r= the number you times by to get to the next term a= 2 √ 2 a= the first term of the sequence What terms have you got/need to find? the 10 th term nth term = arn-1 1 2 3 4. . . 10 ? , 4, ? , 8. . ar 9 9 ar = 9 (√ 2) 2 √ 2 9 10 ar = 2 √ 2 9 5 ar = 2 x 2 9 6 ar = 2 th 10 term= 64

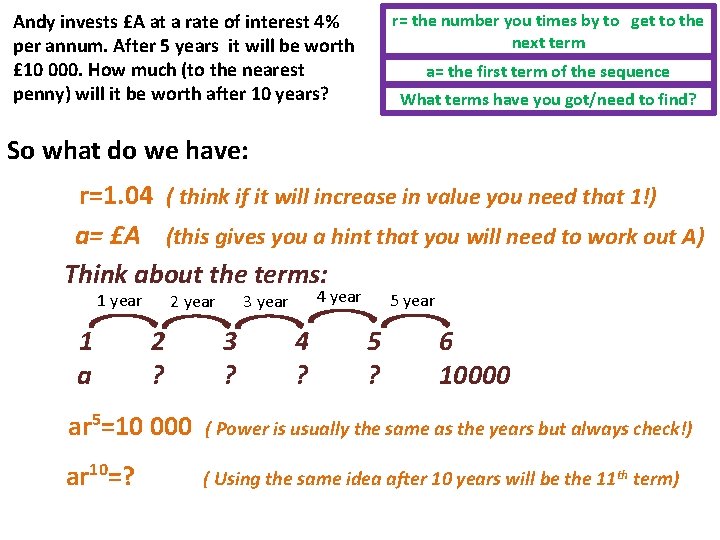
Andy invests £A at a rate of interest 4% per annum. After 5 years it will be worth £ 10 000. How much (to the nearest penny) will it be worth after 10 years? r= the number you times by to get to the next term a= the first term of the sequence What terms have you got/need to find? So what do we have: r=1. 04 ( think if it will increase in value you need that 1!) a= £A (this gives you a hint that you will need to work out A) Think about the terms: 1 year 1 a 2 year 2 ? 4 year 3 ? 4 ? 5 year 5 ? 6 10000 ar 5=10 000 ( Power is usually the same as the years but always check!) ar 10=? ( Using the same idea after 10 years will be the 11 th term)

Andy invests £A at a rate of interest 4% per annum. After 5 years it will be worth £ 10 000. How much (to the nearest penny) will it be worth after 10 years? ax 1. 045=10 000 £A= £ 10 000 1. 045 r= the number you times by to get to the next term a= the first term of the sequence What terms have you got/need to find? ( Replace the r!) £A = £ 8219. 27 ar 10=? £ 10 000 x 1. 0410 = £ 10 000 x 1. 045 ar 10= £ 12166. 53

What is the first term in the geometric progression 3, 6, 12, 24. . To exceed 1 million? r= the number you times by to get to the next term a= the first term of the sequence What terms have you got/need to find? r=2 ( 6 divided by 3) a= 3 nth term = arn-1 > 1000 3 x 2 n-1 > 1000 000 3 n-1> log 2 (1000 000) 3 n-1> 18. 35 (2 dp) n> 19. 35 (2 dp) n = 20 So 20 th term

Geometric Series A geometric series is the sum of a geometric sequence Terms: Sn 1 2 3 4 n-1 n-2 a + ar 2 + ar 3 +. . . . + ar Terms: 1 2 3 4 n-1 n + arn-1 n r. Sn ar + ar 2 + ar 3 + ar 4 +. . . . + ar Sn r. Sn a + ar 2 + ar 3 +. . . . + arn-2 + arn-1 ar + ar 2 + ar 3 + ar 4 +. . . . + arn-1 + arn Sn- r Sn = a-arn Sn(1 -r)= a(1 -rn) Sn = a(1 -rn) 1 -r + arn

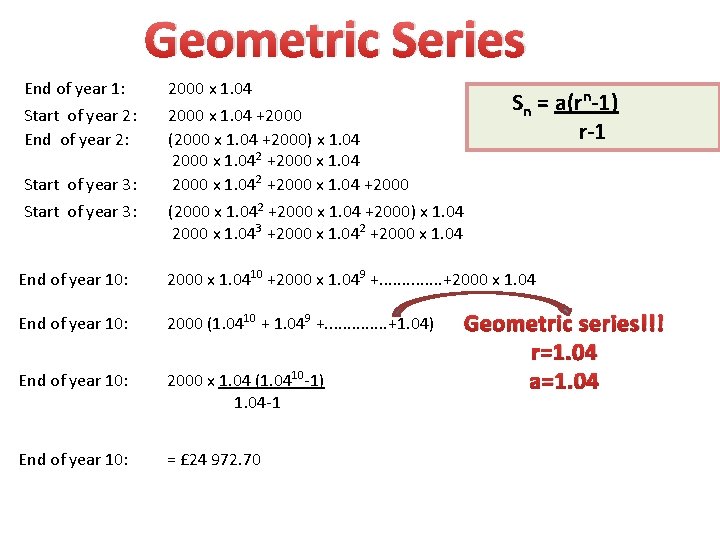
Geometric Series Sn = a(1 -rn) 1 -r Sn = a(rn-1) r-1 An investor invests £ 2000 on January 1 st every year in an account that guarantees 4% per annum, If the interest is calculated on the 31 st of December each year, how much will be in the account at the end of the 10 th year? So using logic break it down to understand what is happening: End of year 1: 2000 x 1. 04 Start of year 2: End of year 2: 2000 x 1. 04 +2000 (2000 x 1. 04 +2000) x 1. 04 2000 x 1. 042 +2000 x 1. 04 +2000 Start of year 3: (2000 x 1. 042 +2000 x 1. 04 +2000) x 1. 04 2000 x 1. 043 +2000 x 1. 042 +2000 x 1. 04

Geometric Series End of year 1: 2000 x 1. 04 Start of year 2: End of year 2: 2000 x 1. 04 +2000 (2000 x 1. 04 +2000) x 1. 04 2000 x 1. 042 +2000 x 1. 04 +2000 Start of year 3: Sn = a(rn-1) r-1 (2000 x 1. 042 +2000 x 1. 04 +2000) x 1. 04 2000 x 1. 043 +2000 x 1. 042 +2000 x 1. 04 End of year 10: 2000 x 1. 0410 +2000 x 1. 049 +. . . +2000 x 1. 04 End of year 10: 2000 (1. 0410 + 1. 049 +. . . +1. 04) End of year 10: 2000 x 1. 04 (1. 0410 -1) 1. 04 -1 End of year 10: = £ 24 972. 70 Geometric series!!! r=1. 04 a=1. 04

Geometric Series Some problems could be described like this The sum of This for. . . . r=1 to 10 Sn = a(rn-1) r-1 = 3 x 21 +3 x 22 +3 x 23 +3 x 24 +3 x 25 +3 x 26 +3 x 27 +3 x 28 +3 x 29 +3 x 210 =3(21 +22 +23 +24 +25 +26 +27 +28 +29 +210) Geometric series!!! r=2 = 3 x 2 (210 -1) a=2 2 -1 S 10 = 6138

Sum to infinity of a convergent Geometric series Convergent means that the series tends towards a specific value as more terms are added. This value is called the limit. Consider this series S= 3 + 1. 5 + 0. 75 + 0. 375 +. . . r= 1 2 a=3 Test for different values of n: As n gets larger S becomes closer to 6

Sum to infinity of a convergent Geometric series This series S= 3 + 1. 5 + 0. 75 + 0. 375 +. . . Is a convergent series. This happens because: -1< r < 1 If this were not true it would not be convergent. Sn = a(1 -rn) 1 -r But if -1< r < 1, as S∞ = a(1 -0) 1 -r S∞ = __a__ 1 -r

nth term = arn-1 Sn = a(1 -rn) 1 -r S∞ = __a__ 1 -r