GCSE Ratio jfrosttiffin kingston sch uk Dr Frost

GCSE : : Ratio jfrost@tiffin. kingston. sch. uk @Dr. Frost. Maths Objectives: Understanding what is meant by ratio. Solve problems where a value and a ratio is given. Combine ratios. Solve problems involving changing ratios. Last modified: 29 th December 2018

www. drfrostmaths. com Everything is completely free. Why not register? Register now to interactively practise questions on this topic, including past paper questions and extension questions (including UKMT). Teachers: you can create student accounts (or students can register themselves), to set work, monitor progress and even create worksheets. With questions by: Dashboard with points, trophies, notifications and student progress. Teaching videos with topic tests to check understanding. Questions organised by topic, difficulty and past paper.

Overview Ratio allows us to express the ‘relative size’ of different quantities. Lesson 1: Simplifying ratios and solving problems where one amount or total is given. Lesson 2: Combining or splitting ratios. Lesson 3: Further Ratio Problem Solving (Advanced) “Javier and Carmen share some money in the ratio 5 : 6. When each are given £ 4 more, the ratio of the money they have is now 6 : 7. How much money did each initially have? ”

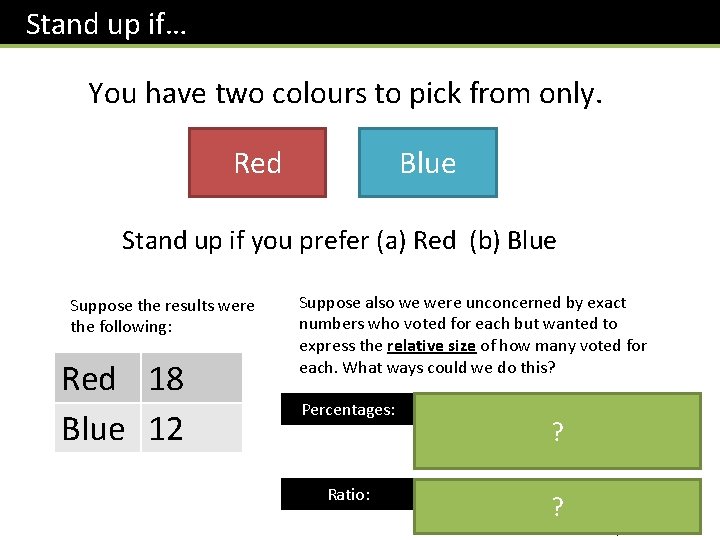
Stand up if… You have two colours to pick from only. Red Blue Stand up if you prefer (a) Red (b) Blue Suppose the results were the following: Red 18 Blue 12 Suppose also we were unconcerned by exact numbers who voted for each but wanted to express the relative size of how many voted for each. What ways could we do this? Percentages: Ratio: Red 60%, Blue 40% ? Percentages are good for indicating proportion of some total. Ratio of red to blue: ? (We’ll explore this on 3: 2 the next slide…)

What is ratio? For each three people who chose What specifically does this mean? red, two chose blue. It could be that we just had 3 red people and 2 blue. The above statement would be true! And similarly we could have 9 red and 6 blue. This means we can times (or divide) each part in the ratio by the same number, and end up with an equivalent ratio.

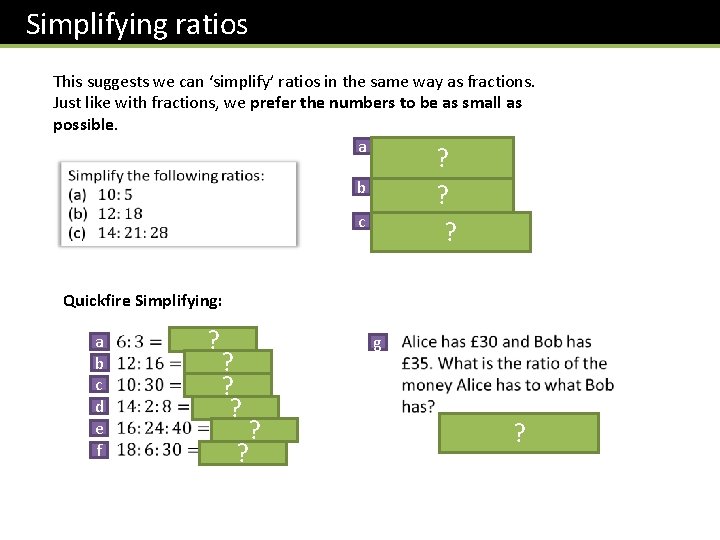
Simplifying ratios This suggests we can ‘simplify’ ratios in the same way as fractions. Just like with fractions, we prefer the numbers to be as small as possible. a ? b ? ? c Quickfire Simplifying: a b c d e f ? ? ? g ?

Splitting an amount into a given ratio Method 1: Identify what ‘ 1 part’ is worth In the ratio 3: 1, we have “ 3 parts muffin” to “ 1 part cupcake”. The given value in the question is the 20 cakes. How many ‘parts’ does this represent? ? 4 parts = 20 1 part = 5 ? 3 parts = 15 ? There are 15 cupcakes. Method 2: The ‘scaling’ way ?

Test Your Understanding Method 1: Identify what ‘ 1 part’ is worth (The one value given is the € 56, which is the total amount Jack and Kate share. So how many parts does this represent? ) 14 parts = € 56 1 part = € 4 ? 6 parts = € 24 Lila gets € 24 Method 2: The ‘scaling’ way ?

When one of the quantities is given In a death match of monkeys vs squirrels, the monkeys outnumber the squirrels by a ratio of 5: 2. There’s 35 monkeys. How many squirrels are there? Method 1: Identify what ‘ 1 part’ is worth The one value given is the 35 monkeys. How many parts in the ratio does this represent? 5 parts = 35 1 part = 7 ? 2 parts = 14 Therefore 14 squirrels. Method 2: The ‘scaling’ way ?

When the difference is given Alice and Bob share some money in the ratio 7: 4. Alice received £ 12 more than Bob. What did they receive in total? Method 1: Identify what ‘ 1 part’ is worth 3 parts = £ 12 1 part = £ 4 11 parts = £ 44 This time £ 12 represents the DIFFERENCE in the parts. ? We want the total amount, so need to find the value of the total parts. Method 2: The ‘scaling’ way ?

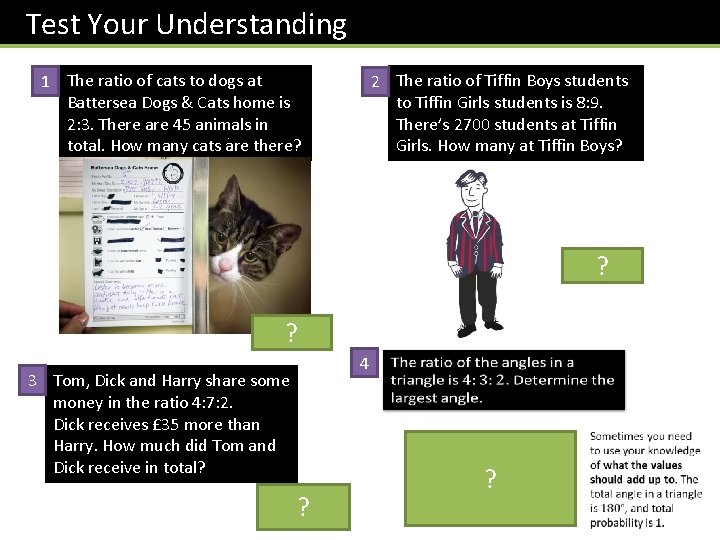
Test Your Understanding 1 The ratio of cats to dogs at Battersea Dogs & Cats home is 2: 3. There are 45 animals in total. How many cats are there? 2 The ratio of Tiffin Boys students to Tiffin Girls students is 8: 9. There’s 2700 students at Tiffin Girls. How many at Tiffin Boys? 2400 ? 18 ? 3 Tom, Dick and Harry share some money in the ratio 4: 7: 2. Dick receives £ 35 more than Harry. How much did Tom and Dick receive in total? £ 77 ? 4 ?

Ratios to/from equations or worded descriptions ? ? The number of yellow balls is twice the number of red balls and the number of green balls is 4 times the number of yellow balls. Determine the ratio of red to yellow to green balls. ?

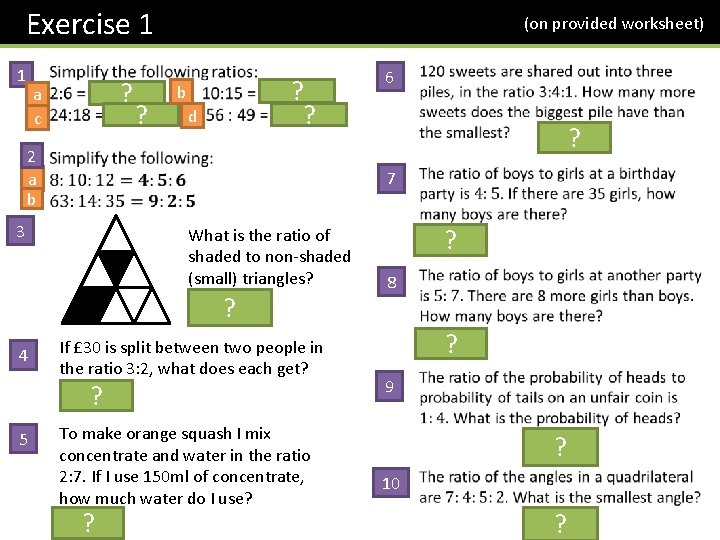
Exercise 1 1 ? a c ? (on provided worksheet) ? ? b d 2 a b What is the ratio of shaded to non-shaded (small) triangles? 2: 6=1: 3 ? If £ 30 is split between two people in the ratio 3: 2, what does each get? £ 18, £ 12 ? 5 ? 7 3 4 6 To make orange squash I mix concentrate and water in the ratio 2: 7. If I use 150 ml of concentrate, how much water do I use? 525 ml ? ? 8 ? 9 ? 10 ?

Exercise 1 (on provided worksheet) 11 14 ? 15 ? 12 ? 16 ? 13 ? 17 ? ?

Combining and Subdividing Ratios One new type of question to the 2017+ GCSE syllabus is combining two ratios into one:

Further Example ?

Test Your Understanding 24 15? 20

Subdividing a Ratio ? ? ?

Test Your Understanding ?

Exercise 2 (on provided worksheet) 4 1 ? ? ? a b c d e 2 ? 5 ? ? 3 6 ? ?

Exercise 2 (on provided worksheet) 9 7 ? ? 8 10 ? ? ?

Updated Ratios after Changing Amounts ?

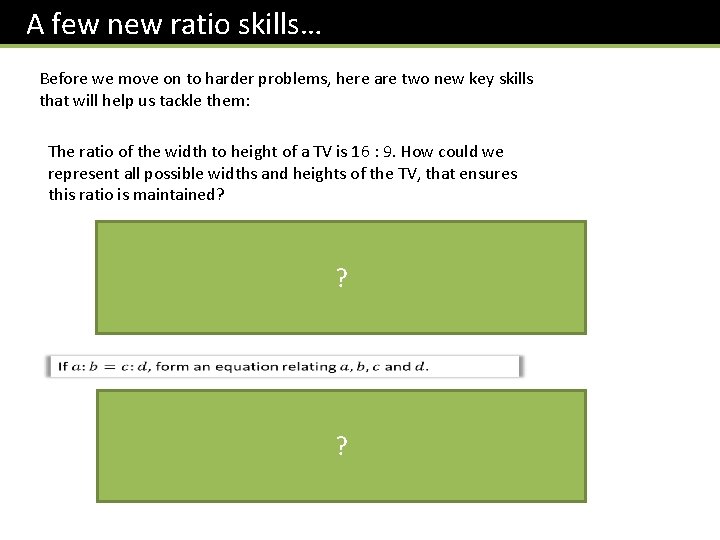
A few new ratio skills… Before we move on to harder problems, here are two new key skills that will help us tackle them: The ratio of the width to height of a TV is 16 : 9. How could we represent all possible widths and heights of the TV, that ensures this ratio is maintained? ? ?

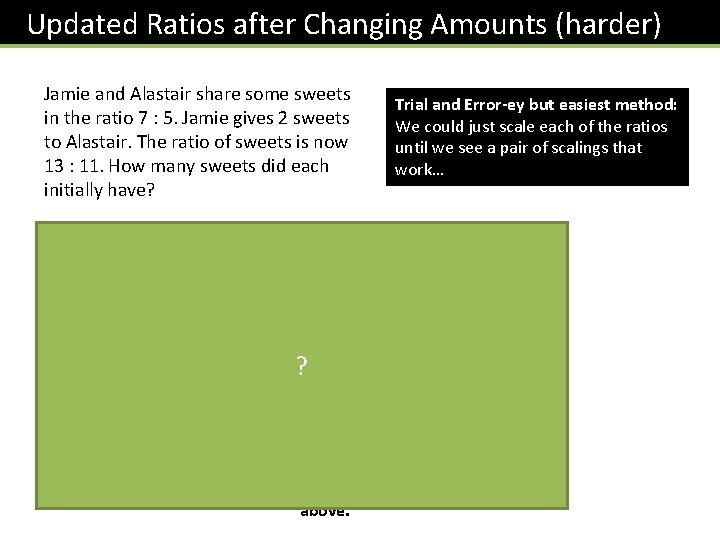
Updated Ratios after Changing Amounts (harder) Jamie and Alastair share some sweets in the ratio 7 : 5. Jamie gives 2 sweets to Alastair. The ratio of sweets is now 13 : 11. How many sweets did each initially have? Possible numbers of sweets before: (multiples of 7 : 5) Jamie 7 14 21 28 35 … Alastair 5 10 15 20 25 Trial and Error-ey but easiest method: We could just scale each of the ratios until we see a pair of scalings that work… Possible numbers of sweets after: (using 13 : 11) Jamie 13 26 ? Alastair 11 22 At this stage we can see that we could have started with 28 and 20 sweets, and after the exchange, each would have 26 and 22, as above.

Updated Ratios after Changing Amounts (harder) Jamie and Alastair share some sweets in the ratio 7 : 5. Jamie gives 2 sweets to Alastair. The ratio of sweets is now 13 : 11. How many sweets did each initially have? But what if we wanted to use an algebraic method? Let’s try and use the two new skills we have just learnt. ? Cross-multiply.

Test Your Understanding Javier and Carmen share some money in the ratio 5 : 6. When each are given £ 4 more, the ratio of the money they have is now 6 : 7. How much money did each initially have? ?

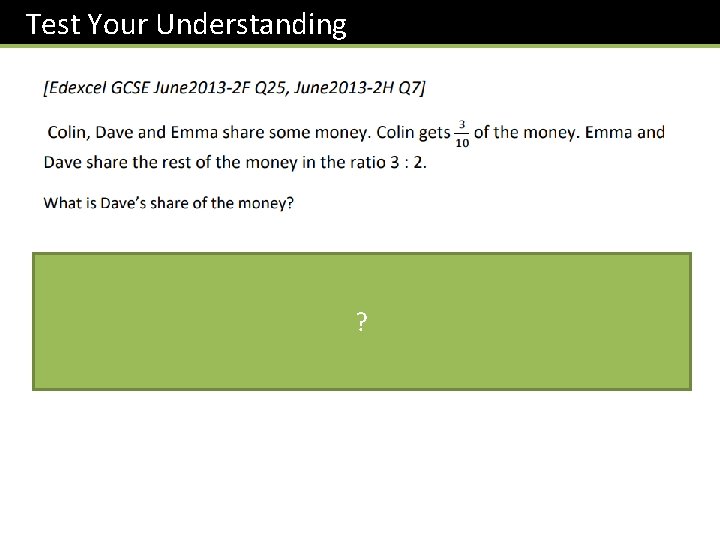
Exercise 3 1 The ratio of red to blue counters is 2 : 5 and there are 40 blue counters. When I remove some red counters the ratio is now 1 : 4. How many red counters did I remove? 16 – 10 = 6 removed (on provided worksheet) 4 ? 2 The ratio of green to yellow beads is 4 : 5, and there are initially 27 beads. I add some yellow beads and the ratio is now 1 : 3. How many yellow beads did I add? 36 – 15 = 21 beads ? 3 The ratio of boys to girls is 1 : 2. Two boys and two girls enter the room and the ratio is now 5 : 9. How many boys and girls were there originally? 8 boys and 16 girls ? The ratio of children to adults on a school trip is initially 10 : 1. This doesn’t meet government regulations, so 5 more children and 5 more adults join the trip so that the ratio is now 9 : 1. How many children are there now? 405 ? 5 [JMO 2015 A 4] My fruit basket contains apples and oranges. The ratio of apples to oranges in the basket is 3 : 8. When I remove one apple the ratio changes to 1 : 3. How many oranges are in the basket? Solution: 24 ?

Exercise 3 (on provided worksheet) 6 N ? [STMC Final 2007/08 Q 1] Anne, Becky and Charlotte had sums of money in the ratio 7: 6: 5. One of them gave £ 9 to one of the others and this changed the ratio (in the same order of names) to 6: 5: 4. The total sum of money remained the same; what was it? Solution: ? £ 810