Gausskeverkmodell Gaussian Mixture Model s tantsa az EMalgoritmussal

Gauss-keverékmodell (Gaussian Mixture Model) és tanítása az EM-algoritmussal

Bevezetés Láttuk, hogyan lehet Gauss-görbét illeszteni adatpontokra De a Gauss-görbe mint modell, nem igazán flexibilis Valós adatok eloszlása ritkán lesz tökéletesen Gauss-os Azaz a „modellezési hiba” nagy lesz Ezért bevezetünk egy új modellt, a Gauss-keverékmodellt Az egyszerű Gauss-görbénél jóval rugalmasabb az alakja Azonban a tanítása sajnos jóval nehezebb lesz Továbbra is a Maximum Likelihood célfüggvényt fogjuk használni Azonban a zárt képletes megoldás nem fog működni, ezért bevezetünk egy iteratív tanítóalgoritmust. Ez lesz az EM-algoritmus Az egyes osztályokhoz tartozó modelleket ismét külön-külön tanítjuk Az előadás arról szól, hogyan lehet a modellt egyetlen osztály példáira illeszteni, ezért ci nem szerepel a jelölésben De ne feledjük , hogy az eljárást minden osztályra meg kell ismételni

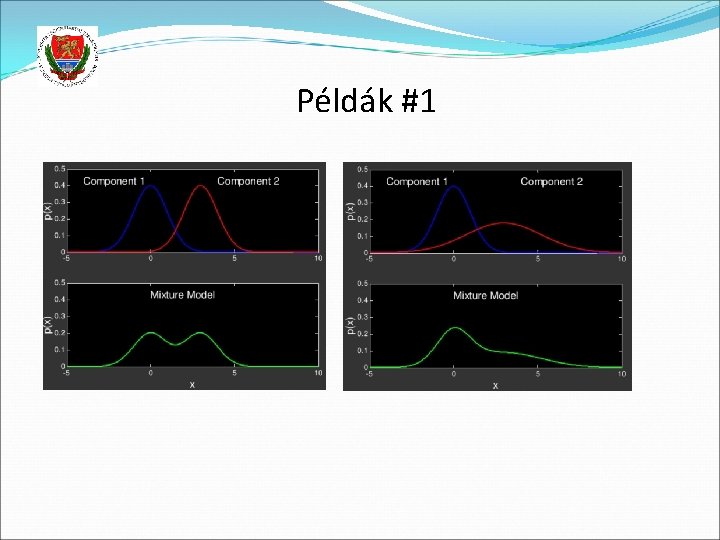
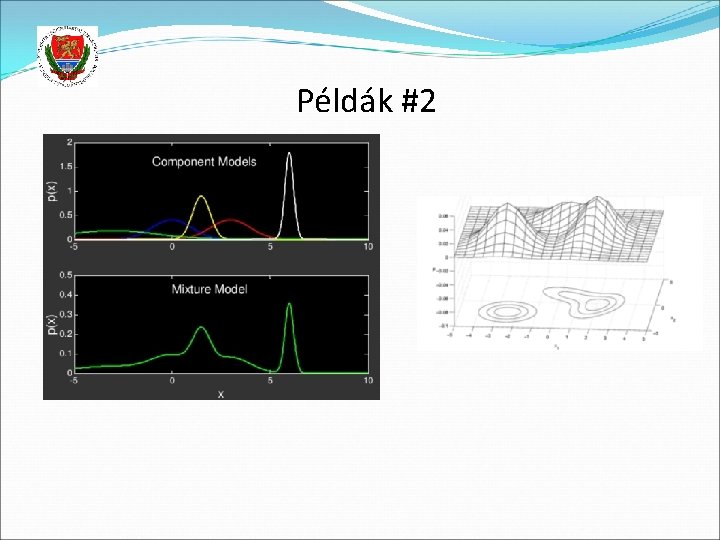
Gaussian Mixture Model (GMM) A p(x) eloszlást Gauss-görbék súlyozott összegével közelítjük Képlettel: Ahol N jelöli a normális (avagy Gauss) eloszást A πk nem negatívok és összegük 1 A Gauss-komponensek K száma rögzített, nekünk kell megadni tanítás előtt (azaz ún. „meta-paraméter”) A komponensek számának növelésével a fenti görbe lényegében bármilyen eloszlást képes közelíteni, azaz jóval rugalmasabb eloszlást ad, mint egyetlen Gauss-görbe Példák:

Példák #1

Példák #2

A GMM paramétereinek becslése A modell paraméterei: πk , μk és Σk minden komponensre (k=1, . . , K). A paramétereket gyakran röviden θ-val fogjuk jelölni: θ=(π1, μ 1 , 1, …, πK, μK , K) A tanítás során ismét a log-likelihood függényt maximalizáljuk: Amikor p(x) egyetlen Gauss-görbe volt, egyszerűen vettük a deriváltját és annak zérushelyét kerestük Sajnos a GMM esetén a deriválás nem fog menni Más megoldásra lesz szükség – ez lesz az EM-algoritmus

A GMM paramétereinek becslése Tekintsük a log-likelihood függvényt És próbáljuk a deriváltat nullává tenni (mondjuk μk-ra nézve): Ez itt a gond (tartalmazza μk-t) 1 Gauss deriváltja (ugyanaz mint korábban) Szóval ez nem megy Egyetlen Gauss esetén a logaritmus kiütötte az exponenciális függvényt De most egy szumma van a logaritmus és az exp között

Egy másik megközelítés – osszuk a pontokat diszjunkt részekre Példa: a zöld pontokra 2 Gauss-ból álló keverékmondellt akarunk illeszteni Osszuk a pontokat 2 diszjunkt csoportra (klaszterre) – ld. lila görbék Ezt megtehetjük pl. a K-means klaszterező algoritmussal Ezután könnyen illeszthetünk 1 -1 Gausst a klaszterekre külön-külön! Az előző órán látott módszerrel

A K-means algoritmus A legközismertebb klaszterező algoritmus A klasztereket 1 -1 pont fogja reprezentálni – a centroid Input: a klaszterezendő pontok, a klaszterek K száma, és egy távolságfüggvény a pontok között 1. lépés: válasszunk K pontot véletlenszerűen centroidnak 2. lépés: minden pontnak találjuk meg a klaszterét (a legközelebbi centroid formájában) 3. lépés: frissítsük a centroidokat az adott klaszterbe tartozó pontok átlagaként 4. step: ha egyetlen pontnak sem változott a klasztere: STOP Else GOTO 2 Example: https: //www. youtube. com/watch? v=RD 0 n. NK 51 Fp 8 3: 00 -tól

K-means helyett „soft clustering” A K-means minden pontot pontosan egy klaszterbe sorol Viszont a Gauss-görbék értéke mindenhol >0, azaz minden pont mindegyik Gauss-komponensbe beletartozik valamennyire A K-means helyett használjunk olyan klaszterező algoritmust, amelyiknél minden pont minden klaszterbe beletartozik, de eltérő súllyal („soft clustering”) A Gauss-görbék illesztését pedig úgy módosítjuk, hogy mindegyik pontot figyelembe eltérő súllyal tudja figyelembe venni A súly [0, 1] közé fog esni, azt kifejezendő, hogy az adott pont milyen valószínűséggel tartozik az adott Gauss-görbéhez Ezt a súlyt znk fogja jelölni, és a k-adik Gauss xn mintára vonatkozó felelőssége („responsibility”) lesz a neve

Gauss-görbék illesztése a súlyok figyelembe vételével Az illesztéshez a k-adik Gauss likelihood függvényét -ra módosítjuk -ról znk=1: az ilyen súlyú pontokra a képlet változatlan znk=0: az adott pont nem befolyásolja képletet Ezzel a log-likelihood helyett lesz (a log. P értékek összege helyett azok súlyozott összege) A derivált is hasonlóan módosul: egy összeg helyett egy súlyozott összeg lesz A derivált zérushelyét ki tudjuk számolni, megoldás a következő dián

A paramétereket becslő formulák Vegyük észre, hogy nagyon hasonló ahhoz, amit 1 Gauss esetén kaptunk az előző órán (csak összegzés helyett súlyozott összegzés szerepel)! Könnyen ki tudjuk számolni, ha a znk értékek adottak

A responsibility értékek kiszámítása Kellene nekünk egy „soft” klaszterező algoritmus De adott Gauss-görbék esetén tkp. a görbékből is vissza tudnánk számolni a znk súlyokat A znk ”responsibility” értékek azt fejezik ki, hogy adott xn pont mennyire tartozik a k-adik Gauss-görbéhez Hogyan tudjuk ezt formalizálni? Ez szimplán a k-adik Gauss-komponens likelihood értéke Amit azért osztunk le a teljes modell likelihood értékével, hogy [0, 1] közé normalizáljuk Tehát maguk a Gauss-komponensek is definiálnak egy klaszterezést Ehhez viszont ismerni kell a komponensek μk és Σk paramétereit!

Az iteratív EM tanítóeljárás Összegezzük, hol is tartunk? A Gaussian-görbéket könnyedén tudjuk illeszteni a pontokra (azaz megbecsülni μk és Σk értékét), ha a responsibility értékek adottak A responsibility értékeket könnyen ki tudjuk számolni, ha a Gauss- görbék (azaz μk és Σk ) adottak Ezekből egy iteratív eljárás rakható össze – az EM-algoritmus 0. lépés: μk és Σk inicializálása (random, vagy K-means-szel) 1. lépés: (E avagy Estimation lépés): a responsibility-k becslése 2. lépés: (M avagy Maximization lépés): maximalizáljuk a Gaussian log-likelihood értékét μk és Σk újraszámolásával GOTO 1. lépés (μk és Σk megváltozott, ezért újra kell számolnunk a responsibility értékeket!)

Egy másik lehetséges értelmezés Emlékezzünk, hogy megpróbáltuk a log-likelihood függvény deriválni, de elakadtunk: Itt a gond (tartalmazza μk-t) Vegyük észre, hogy a problémás kifejezés megegyezik a “responsibility” értékével! Csaljunk: tegyünk úgy, mintha ez μk-tól független konstans lenne Ekkor könnyen ki tudjuk számolni a deriváltat, és így μk –t (és ez Σk esetén is igaz ) Viszont amit kapunk, nem lesz optimális, mert csaltunk Ezért újraszámoljuk a responsibility értékeket, és megismételjük a számítást (újra és újra)

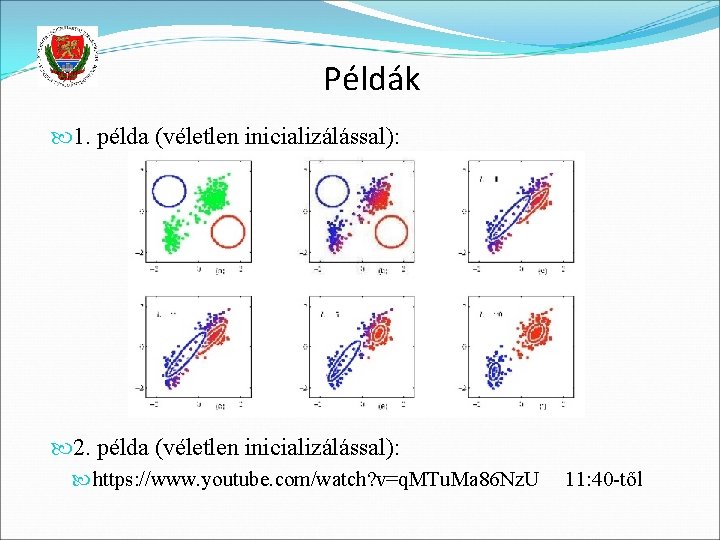
Példák 1. példa (véletlen inicializálással): 2. példa (véletlen inicializálással): https: //www. youtube. com/watch? v=q. MTu. Ma 86 Nz. U 11: 40 -től

Az EM-algoritmus igazolása A leírt megoldás kétségkívül végrehajtható, de honnan tudjuk, hogy konvergál a helyes megoldáshoz? A következőkben bebizonyítjuk, hogy a log-likelihood érték minden egyes iterációs lépésben csak nőhet Ezáltal a teljes eljárás lokális optimum megtalálását garantálja A bizonyítás általános, azaz nem csak GMM-ekre működik, hanem bármely modellre, ami ilyen alakba írható: (Megjegyzés: a GMM πk súlyai nemnegatívak és összegük 1, ezért P(k) diszkrét eloszlásként értelmezhetők )

A maximalizálási lépés formalizálása Eddig azt mondtuk, hogy a Gauss-görbéket paramétereit külön optimalizáljuk, a likelihood maximalizálásával Ezt egyetlen formulával úgy tudjuk felírni, mint az eloszlások szorzatának maximalizálása Véve a logaritmust, a log-likelihood függvényre ezt kapjuk: Ahol znk annak a valószínűsége, hogy az xn minta a k. komponenshez tartozik. A továbbiakban ezt P θ(k| xn) jelöli:

További jelölésbeli módosítások Eddig a paramétereket θ jelölte. Az alábbiakban részletesebben elemezzük, hogy mi történik az M optimizálási lépésben. Hogy megkülönböztessük az optimalizálás előtti és utáni értékeket, az aktuális paramétereket θ’, a maximalizálással kapott új paramétereket pedig θ fogja jelölni Összegezve tehát, célünk a log-likelihood maximalizálása Ehelyett az alábbit maximalizáljuk minden iterációs lépésben: Fontos, hogy θ’ rögzített és θ az optimalizálandó változó!

Expectation maximization A függvényt, amelyet maximalizálunk „expectation” függvénynek is hívják, mivel ez a feltételes várható értéke adott xn tanítópéldák és θ’ esetén függvény Ezzel a jelöléssel az EM-algoritmus két lépése: 1. Expectation (avagy estimation) lépés: kiszámoljuk a értékeket rögzített θ’ mellett, mivel szükségesek a fenti függvény számításához 2. Maximalizálási lépés: maximalizáljuk a fenti függvényt θ -ra nézve

Az EM-algoritmus igazolása Tehát, maximalizálni szeretnénk a log-likelihood értékét: De ehelyett ezt maximalizáljuk: Megmutatjuk, hogy ha a maximalizálási lépés növeli az expectation függvény értékét, azaz a régi θ’ és az új és θ esetén Akkor Azaz ha a maximalizálási lépés után kapott új expectation érték nagyobb, mint a korábbi, akkor az új log-likelihood érték is nagyobb, mint a korábbi

Bizonyítás (röviden) A bizonyítás megmutatja, hogy Azaz Ha akkor A bizonyítás miatt ekkor Amiből átrendezéssel következik, hogy

Bizonyítás (részletesen) =1 ≤ 0 (Jensen-inequality)

A kulcs a Jensen-egyenlőtlenség Általánosan, tetszőleges p(x) és q(x) eloszlásokra: Speciálisan, ebben az esetben:

Összegzés – az EM-algoritmus Bármilyen modell optimalizálására jó, amely ilyen alakú: A log-likelihood függvény helyett az expectation függvényt maximalizálja Iteratív eljárás Minden iterációs lépésben az aktuális θ’ paraméterek mellett olyan új θ paramétereket talál, amelyekre az expectation értéke nagyobb (nem kisebb) Két lépése: expectation (vagy estimation) és maximization Garantált, hogy a log-likelihood minden lépésben nő (nem csökken), ezáltal lokális optimumba vezet Az optimalizálási formulákat minden modellre külön-külön le kell vezetni

Technikai megjegyzések A paramétereket gyakran K-means klaszterezéssel inicializáljuk Ez nagyon eltérő eredményeket adhat a centroidok inicializálásától függően Ezért érdemes a klaszterezést többször lefuttatni eltérő (pl. random) inicializálással Ezután az EM-algoritmust abból a klaszterezésből indítjuk, amelyik a legnagyobb kezdeti log-likelihood értéket adja A véletlen incializálásnál persze léteznek kifinomultabb inicializálási megoldások is a K-means klaszterezéshez

Technikai megjegyzések 2 Feltételeztük, hogy a Gauss-ok száma (a K paraméter) előre adott Persze automatikusan is meg lehet próbálni megtalálni Legegyszerűbb megoldás: próbáljunk 1, 2, 3, … Gauss-t illeszteni A legnagyobb log-likelihood-ot adó modellt válassszuk Milyen hibát eredményez, ha K-t túl kicsinek választjuk? Az algoritmus lefut, de szuboptimális eredménnyel

Technikai megjegyzések 3 Mi történik, ha K-t túl nagyra választjuk? Klaszter vagy klaszterek üresen maradhatnak De már az is baj, ha egy klaszterbe túl kevés pont esik a kovarianciamátrix nem invertálható szingularitási probléma pl. : egyetlen példának mennyi a szórása? Emiatt az algoritmus nagyon érzékeny az „outlier” példákra

Technikai megjegyzések 4 A gyakorlatban sokszor diagonális kovarianciamátrixúra korlátozzuk a Gauss-komponenseket A szinguláris kov. mátrix esete kisebb eséllyel következik be A tanítás gyorsabbá válik Minden iterciós lépésben újra kell becsülnünk a kovarianciamátrixot, aztán pedig invertálni ez diagonális mátrixszal jóval gyorsabb A modellezési hibát több komponens megengedésével csökkenthetjük