for s1 for EMwaves total energy density of



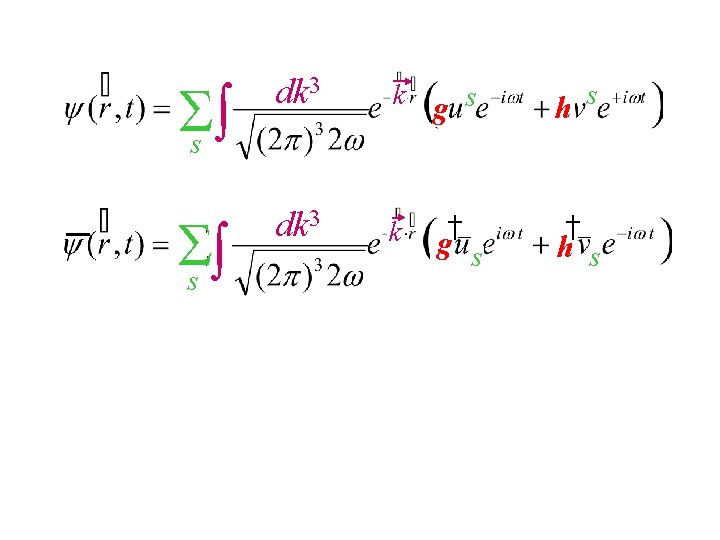










- Slides: 17

for s=1 for EM-waves total energy density: # of photons the Klein-Gordon equation: wave number vector:

for FREE ELECTRONS (or any Dirac, i. e. spin ½ particle: muons, taus, quarks) ± 1 or 1, 2 electrons positrons u v a spinor satisfying: v u Note for each: i. e. we write with -s -E, -p for u 3, u 4 Notice: now we express all terms of the “physical” (positive) energy of positrons!

The most GENERAL solutions will be LINEAR COMBINATIONS s dk 3 k g s h s linear expansion coefficients where g g(k, s), h h(k, s), Insisting { (r, t), (r´, t)}= { †(r, t), †(r´, t)}=0 (in recognition of the Pauli exclusion principal), or, equivalently: { (r, t), †(r´, t)} =d 3(r – r ) respecting the condition on Fourier conjugate fields: forces the g, h to obey the same basic commutation relation (in the “conjugate” momentum space) the g g(k, s), h h(k, s) “coefficients” cannot simple be numbers!
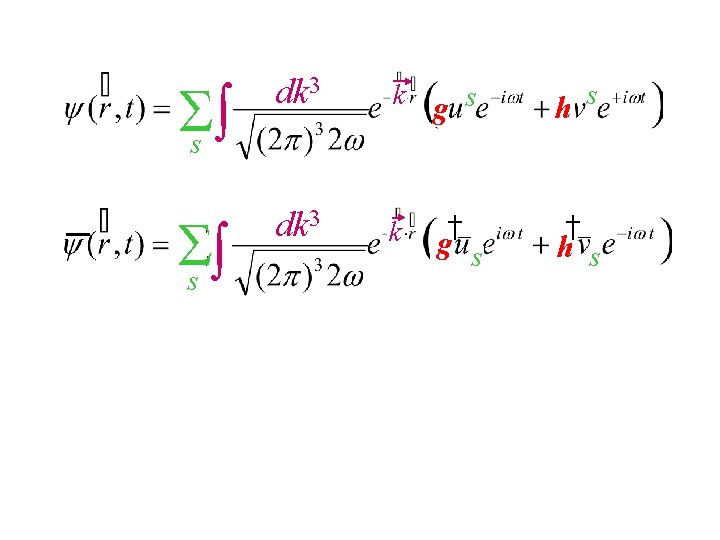
s dk 3 k g s s dk 3 k † g s h s † h s

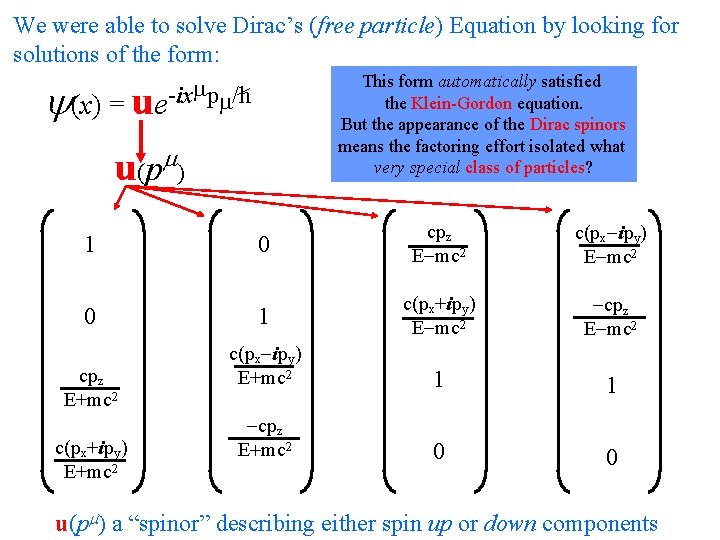
We were able to solve Dirac’s (free particle) Equation by looking for solutions of the form: This form automatically satisfied the Klein-Gordon equation. (x) = e-ix p /h u u (p 1 0 cpz E+mc 2 c(px+ipy) E+mc 2 But the appearance of the Dirac spinors means the factoring effort isolated what very special class of particles? ) 0 cpz E-mc 2 c(px-ipy) E-mc 2 1 c(px+ipy) E-mc 2 -cpz E-mc 2 c(px-ipy) E+mc 2 1 1 -cpz E+mc 2 0 0 u(p ) a “spinor” describing either spin up or down components

What about vector (spin 1) particles? The fundamental mediators of forces: the VECTOR BOSONS Again try to look for solutions of the form p /h -i x (x) = (p)e Polarization vector (again characterizing SPIN somehow) but by just returning to the Dirac-factored form of the Klein-Gordon equation, will we learn anything new? What about MASSLESS vector particles? (the photon!) the Klein-Gordon equation: becomes: or =0 2 Where the d’Alembertian operator: 2

=0 2 is a differential equation you have already solved in Mechanics and E & M Classical Electrodynamics J. D. Jackson (Wiley) derives the relativistic (4 -vector) expressions for Maxwells’ equations can both be guaranteed by introducing the scalar V and vector A “potentials” which form a 4 -vector: (V; A) along with the charge and current densities: (c ; J) Then the single relation: completely summarizes:

(of zero gravitational potential energy) Potentials can be changed by a constant for example, the arbitrary assignment or even leaving everything invariant. In solving problems this gives us the flexibility to “adjust” potentials for our convenience 0 The Lorentz Gauge The Coulomb Gauge 0 In the Lorentz Gauge: 0 and a FREE PHOTON satisfies: a “vector particle” with 4 components (V; A) The VECTOR POTENTIAL from E&M is the wave function in quantum mechanics for the free photon!

so continuing (with our assumed form of a solution) (p) like the Dirac u, a polarization vector characterizing spin Substituting into our specialized Klein-Gordon equation: (for massless vector particles) E 2=p 2 c 2 just as it should for a massless particle!

(p) Like we saw with the Dirac u before, has components! How many? 4 The Lorentz gauge constrains but not all of them are independent! A 0 p = 0 p 0 0 - . p = 0 while the Coulomb Gauge A=0 which you should p = 0 recognize as the familiar condition only for on em waves free photons Obviously only 2 of these 3 -dim vectors can be linearly independent such that p = 0 Why can’t we have a basis of 3 distinct polarization directions? We’re trying to describe spin 1 particles! (mspin = -1, 0, 1)

spin 1 particles: mspin = -1 , 0 , +1 antialigned The m=0 imposes a harsher constraint (adding yet another zero to all the constraints on the previous page!) v=c The masslessness of our vector particle implies ? ? ? In the photon’s own frame longitudinal distances collapse. How can you distinguish mspin = 1 ? Furthermore: with no frame traveling faster than c, can never change a ’s spin by changing frames. What 2 independent polarizations are then possible?

The most general solution: s where s = 1, 2 or s = 1 moving forward Notice here: no separate ANTI-PARTICLE (just one kind of particle with 2 spin states) Massless force carriers have no anti-particles. moving backward

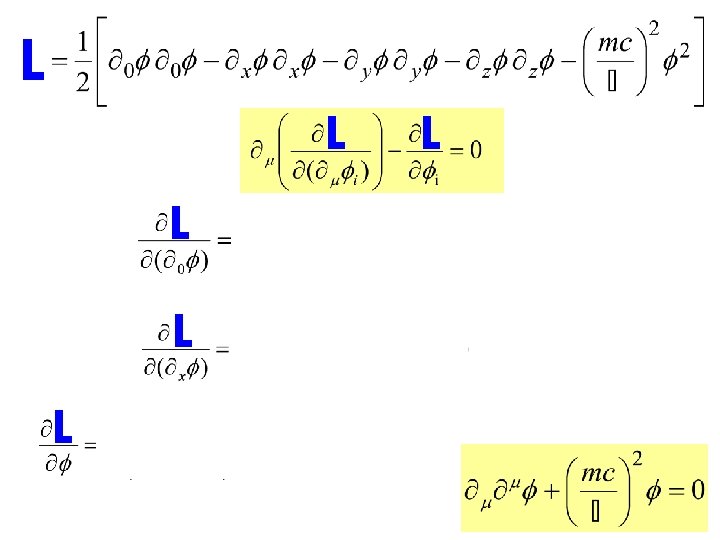
Finding a Klein-Gordon Lagrangian or The Klein-Gordon Equation Provided we can identify the appropriate this should be derivable by The Euler-Lagrange Equation L L L

I claim the expression L serves this purpose

L L L L

You can show (and will for homework!) show the Dirac Equation can be derived from: L DIRAC (r, t) We might expect a realistic Lagrangian that involves systems of particles L(r, t) = L K-G describes photons + L DIRAC describes e+e- objects but each term describes free non-interacting particles L + L INT But what does terms look like? How do we introduce the interactions the experience?

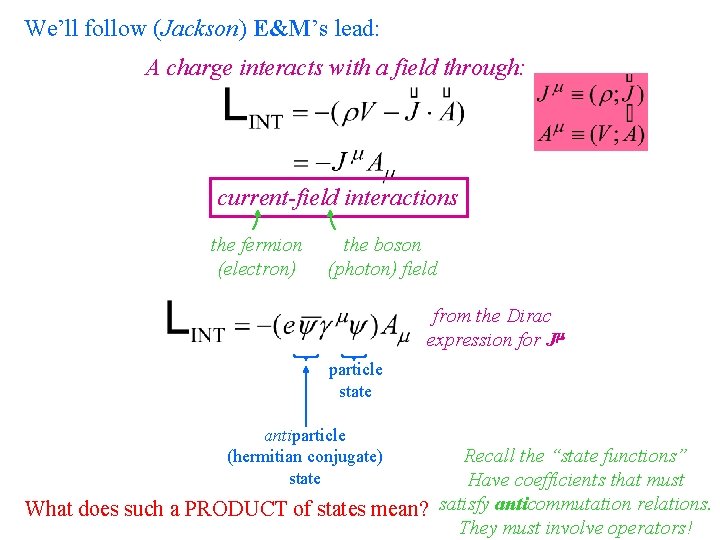
We’ll follow (Jackson) E&M’s lead: A charge interacts with a field through: current-field interactions the fermion (electron) the boson (photon) field from the Dirac expression for J particle state antiparticle (hermitian conjugate) state Recall the “state functions” Have coefficients that must What does such a PRODUCT of states mean? satisfy anticommutation relations. They must involve operators!
 Ratio of useful energy to total input energy
Ratio of useful energy to total input energy Sp gravity
Sp gravity Planar atomic density bcc 111
Planar atomic density bcc 111 Physiological density vs arithmetic density
Physiological density vs arithmetic density Linear density and planar density
Linear density and planar density Nda full dac
Nda full dac What does arithmetic density tell us
What does arithmetic density tell us Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Activo promedio
Activo promedio Total revenues minus total costs equals
Total revenues minus total costs equals Total revenues minus total costs equals
Total revenues minus total costs equals Total revenues minus total costs equals
Total revenues minus total costs equals Total revenue minus total expenses
Total revenue minus total expenses Inductance of coaxial cable
Inductance of coaxial cable Energy density electromagnetic wave
Energy density electromagnetic wave Xkcd uranium energy density
Xkcd uranium energy density Hertz experiment electromagnetic waves
Hertz experiment electromagnetic waves

































