Linear and Planar Atomic Densities Linear Density Directional

- Slides: 8

Linear and Planar Atomic Densities Linear Density: Directional equivalency is related to the atomic linear density in the sense that equivalent directions have identical linear densities. The direction vector is positioned so as to pass through atom centers. The fraction of line length intersected by these atoms is equal to the linear density. Planar Density: Crystallographic planes that are equivalent have the same atomic planar density. The plane of interest is positioned so as to pass through atom centers. Planar density is the fraction of total crystallographic plane area that is occupied by atoms. Linear and planar densities are one- and two-dimensional analogs of the atomic packing factor. Chapter 3 -

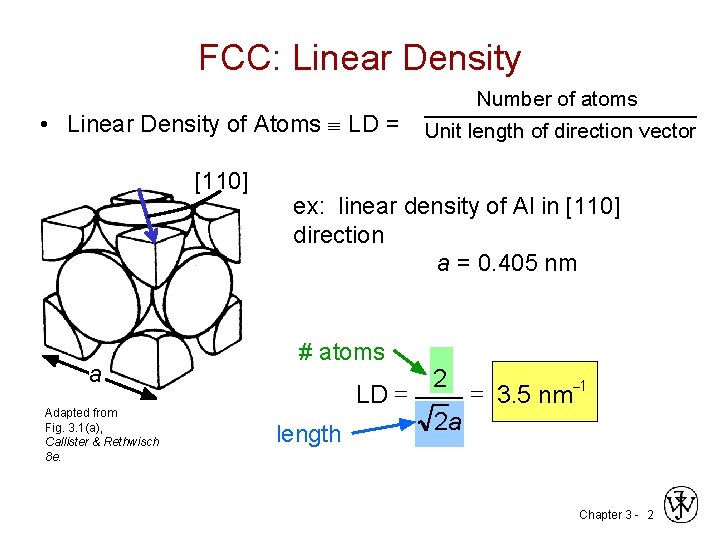
FCC: Linear Density Number of atoms • Linear Density of Atoms LD = Unit length of direction vector [110] a Adapted from Fig. 3. 1(a), Callister & Rethwisch 8 e. ex: linear density of Al in [110] direction a = 0. 405 nm # atoms LD = length 2 2 a = 3. 5 nm-1 Chapter 3 - 2

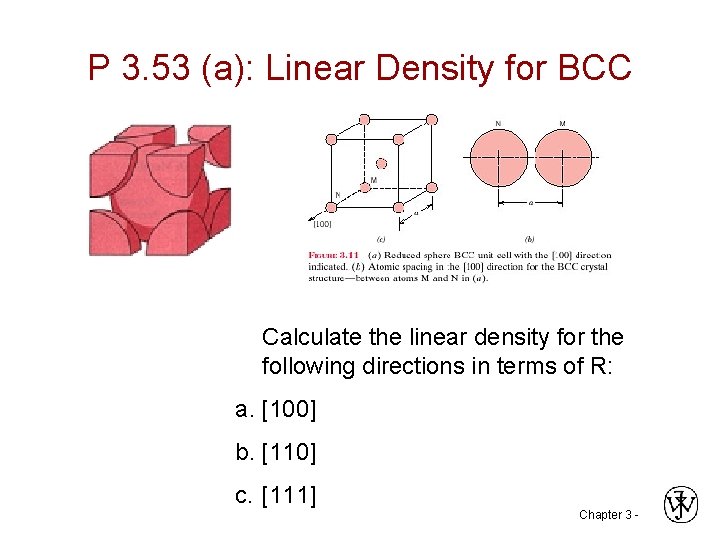
P 3. 53 (a): Linear Density for BCC Calculate the linear density for the following directions in terms of R: a. [100] b. [110] c. [111] Chapter 3 -

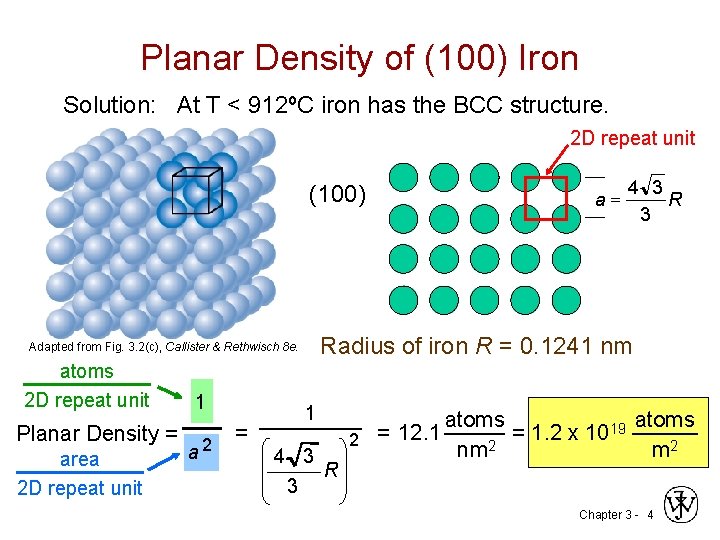
Planar Density of (100) Iron Solution: At T < 912ºC iron has the BCC structure. 2 D repeat unit (100) 1 Planar Density = 2 a area 2 D repeat unit = 4 3 Radius of iron R = 0. 1241 nm Adapted from Fig. 3. 2(c), Callister & Rethwisch 8 e. atoms 2 D repeat unit a= 1 4 3 R 3 atoms 19 = 1. 2 x 10 2 = 12. 1 2 nm m 2 Chapter 3 - 4

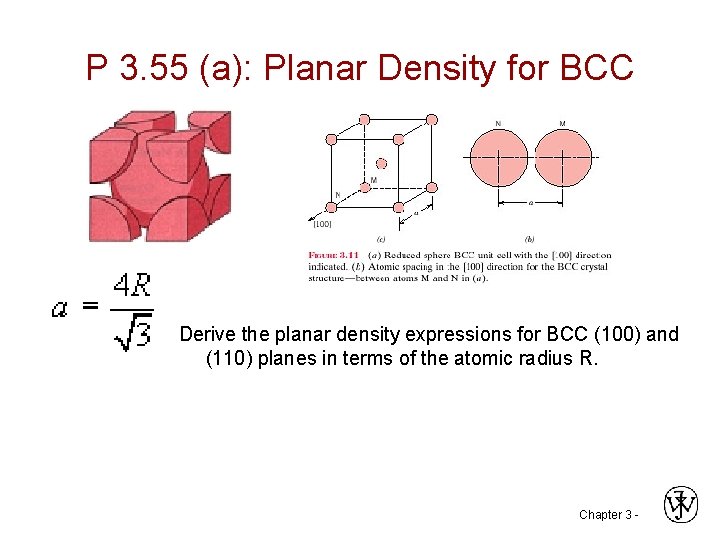
P 3. 55 (a): Planar Density for BCC Derive the planar density expressions for BCC (100) and (110) planes in terms of the atomic radius R. Chapter 3 -

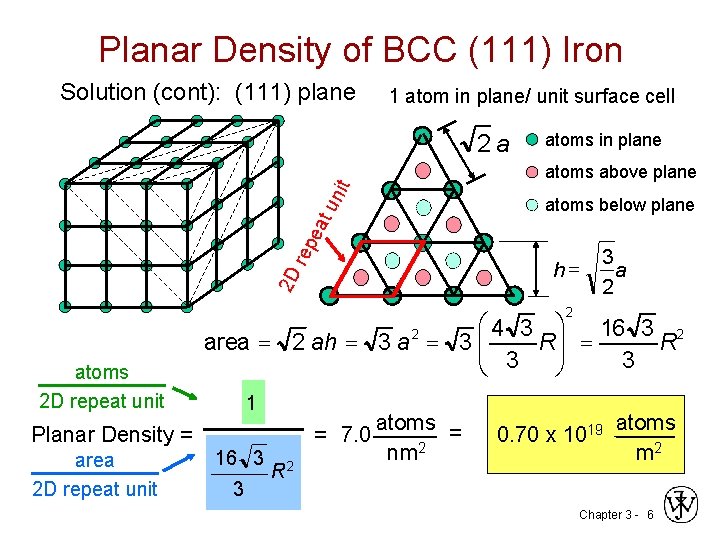
Planar Density of BCC (111) Iron Solution (cont): (111) plane 1 atom in plane/ unit surface cell 2 a atoms in plane un it atoms above plane re pe at atoms below plane 2 D h= 3 a 2 2 atoms 2 D repeat unit Planar Density = area 2 D repeat unit æ 4 3 ö 16 3 2 2 area = 2 ah = 3 a = 3 çç R = R 3 è 3 ø 1 16 3 3 = 7. 0 R 2 atoms = nm 2 0. 70 x 1019 atoms m 2 Chapter 3 - 6

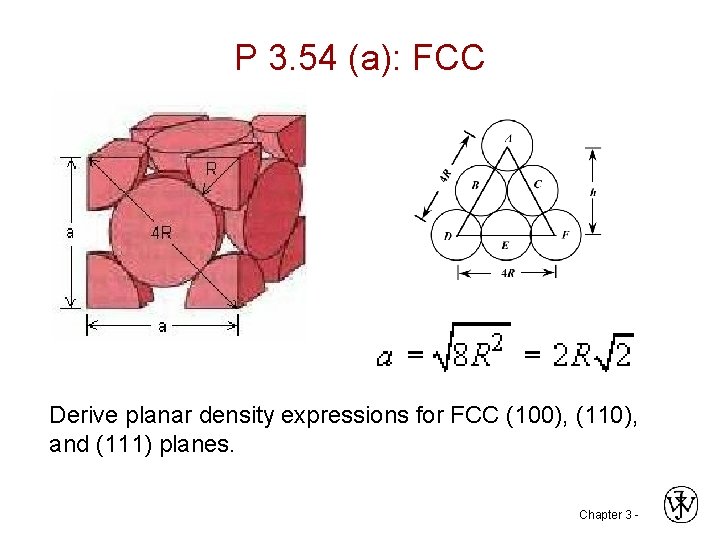
P 3. 54 (a): FCC Derive planar density expressions for FCC (100), (110), and (111) planes. Chapter 3 -

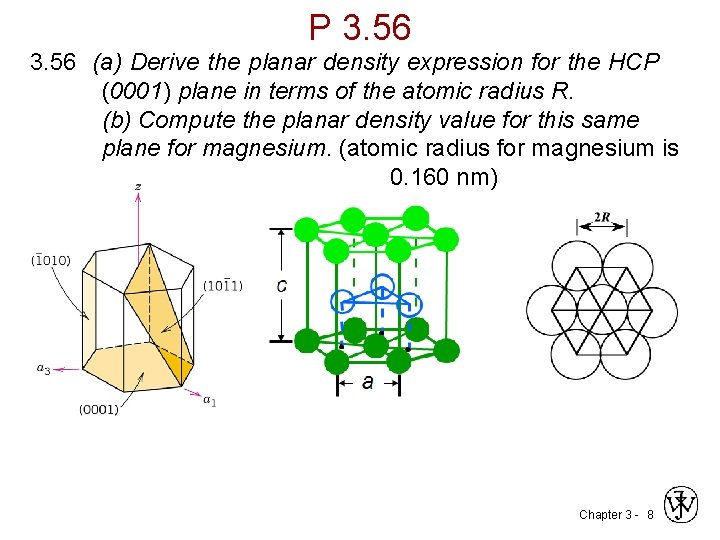
P 3. 56 (a) Derive the planar density expression for the HCP (0001) plane in terms of the atomic radius R. (b) Compute the planar density value for this same plane for magnesium. (atomic radius for magnesium is 0. 160 nm) Chapter 3 - 8
 Planar atomic density fcc 111
Planar atomic density fcc 111 Linear atomic density
Linear atomic density Hypothesis starter
Hypothesis starter Example of statement of the problem in research
Example of statement of the problem in research Directional and non directional hypothesis
Directional and non directional hypothesis Formulating and clarifying the research topic
Formulating and clarifying the research topic What is directional and non directional hypothesis
What is directional and non directional hypothesis Directional and non directional hypothesis
Directional and non directional hypothesis Tetrahedral vs trigonal planar
Tetrahedral vs trigonal planar