Folding Programs Erik Demaine CSAIL MIT Geometric Folding

Folding Programs Erik Demaine CSAIL, MIT

Geometric Folding Algorithms Linkages Paper Polyhedra

Hinged Dissection Universality [Abbott, Abel, Charlton, Demaine, Kominers 2008] · Theorem: For any finite set of polygons of equal area, there is a hinged dissection that can fold into any of the polygons, continuously without self-intersection ▪ Number of pieces is pseudopolynomial (optimal)

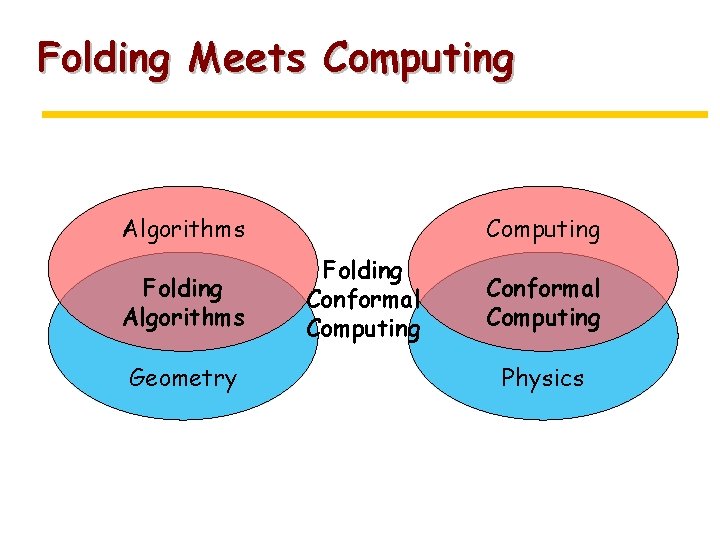
Folding Meets Computing Algorithms Folding Algorithms Geometry Computing Folding Conformal Computing Physics

Mesoscale Hinged Dissection [Mao, Thalladi, Wolfe, Whitesides 2002]

DNA Folding · Synthetic DNA to fold into desired polygon [Rothemund — Nature 2006] ~100 nm

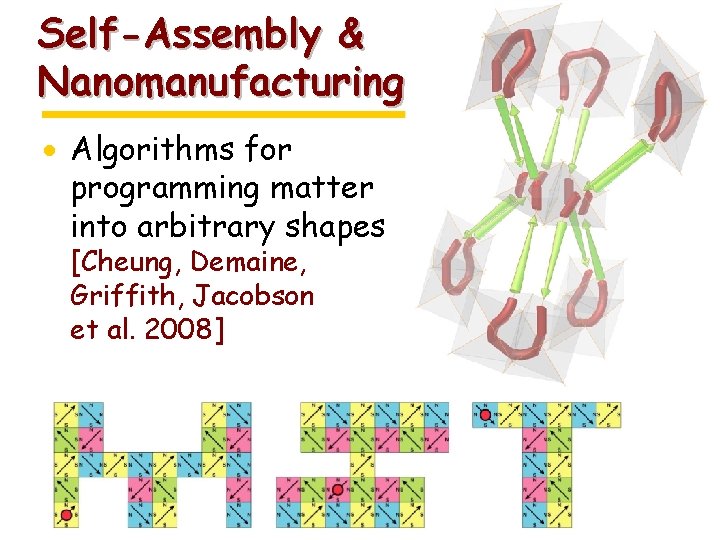
Self-Assembly & Nanomanufacturing · Algorithms for programming matter into arbitrary shapes [Cheung, Demaine, Griffith, Jacobson et al. 2008]

Self-Assembly of Sorting Circuit

Self-Assembly of Sorting Circuit

Folding Programs · Folding assembly process is useful for more than assembly · Can reprogram an already-assembled device by “feeding” program (circuit)

Operating System · High-level goals: ▪ Load programs/circuits ▪ Destroy programs/circuits ▪ Communication channels between running programs/circuits · Challenges: ▪ Embedding programs onto hardware ▪ Routing “reprogramming” instructions ▪ Feedback from program to OS (spawn)

Asynchronous Logic Automaton · 2 bits = which gate (4) · 3 bits for input 1 (8 neighbors including diagonal) · 3 bits for input 2 · Bit = 0 wire and 1 wire ▪ Neither occupied => ready ▪ 0 wire occupied => 0 input ▪ 1 wire occupied => 1 input ▪ Both wires occupied: unused

Reprogrammable Asynchronous Logic Automaton · Simple solution: ▪ Bigger rule table, more states, more wires · Ideally: ▪ Simple rules ▪ Small number of additional states ▪ Use 0+1 for reprogramming; no extra wires · Somewhere in the middle: von Neumann’s Universal Constructor (self-replicating cellular automaton)

One Solution · Regular state (AND/OR/etc. ) ▪ 0+1 switches to reset state · Reset state ▪ Accept AND/OR/etc. ; programs next regular state ▪ Then accept N/E/W/S forwarding direction ▪ Once programmed, auto-switch to forward state · Forward state ▪ Send 0+1 to N/E/W/S to turn next cell to reset state ▪ Then pass on all input bits (0/1) to next cell ▪ 0+1 switches to ready state, which ignores 0/1 inputs ▪ Last node in chain sends back final 0+1 stream to switch ready state to regular state

Ongoing Work · · · Converting data to programs Cleaner integration of logic & programming Hierarchical programming Simulation Design & develop full operating system within this framework