Exercise Simplify 22 4 Exercise Simplify 22 4
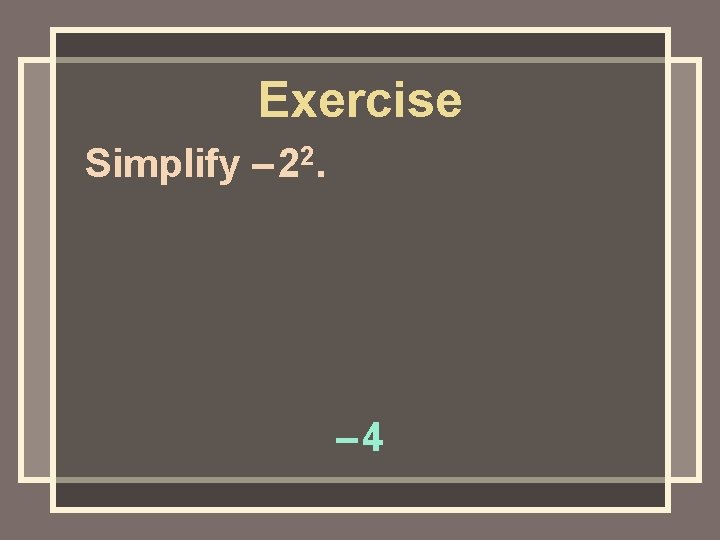

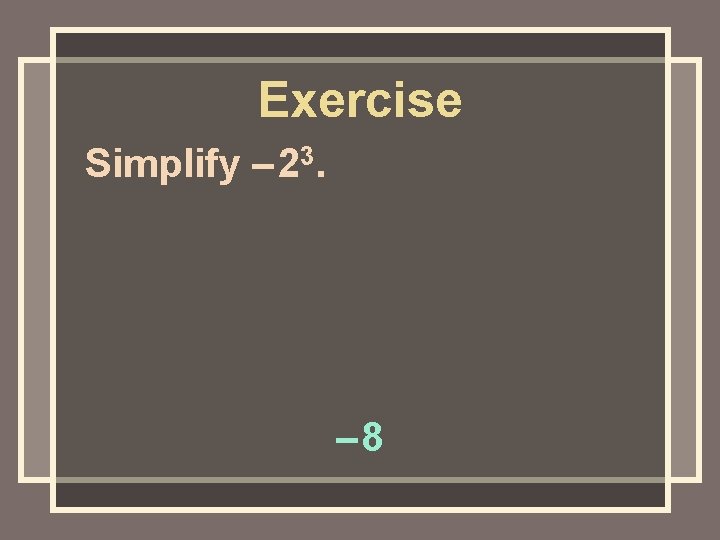
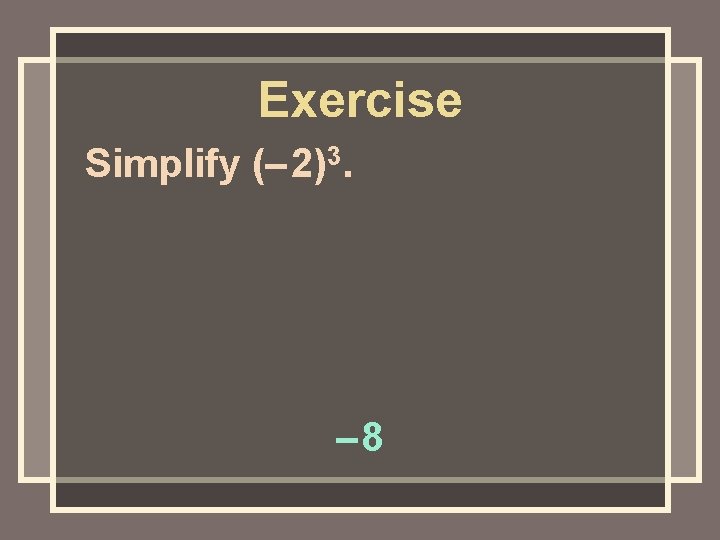







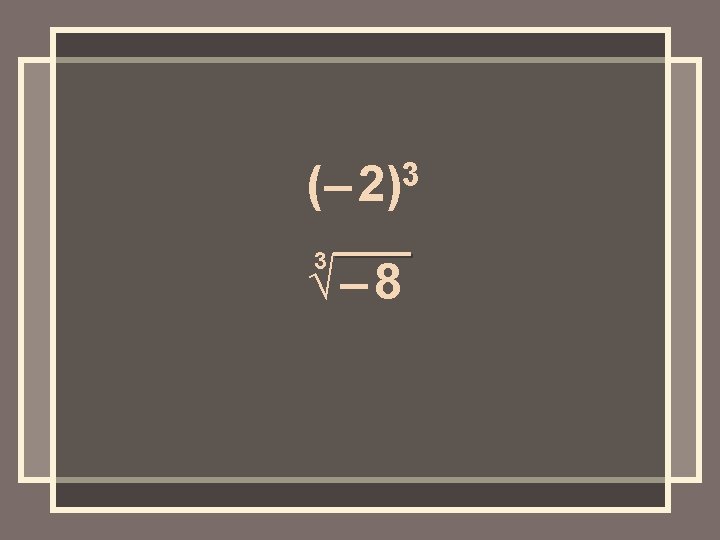









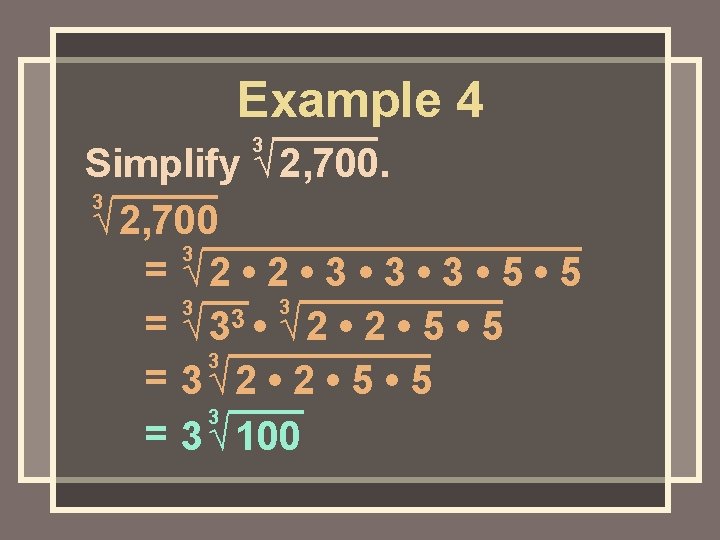




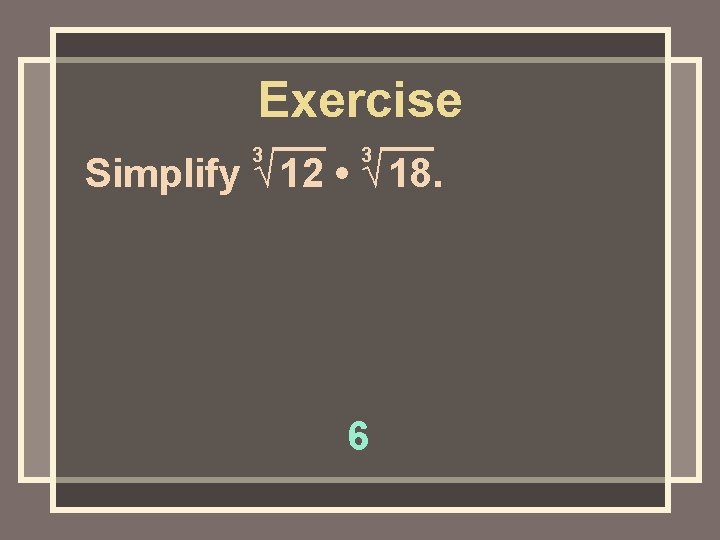
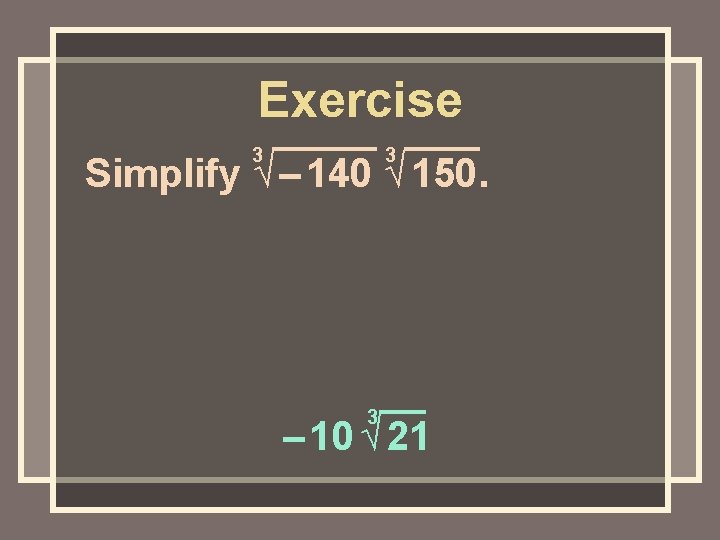
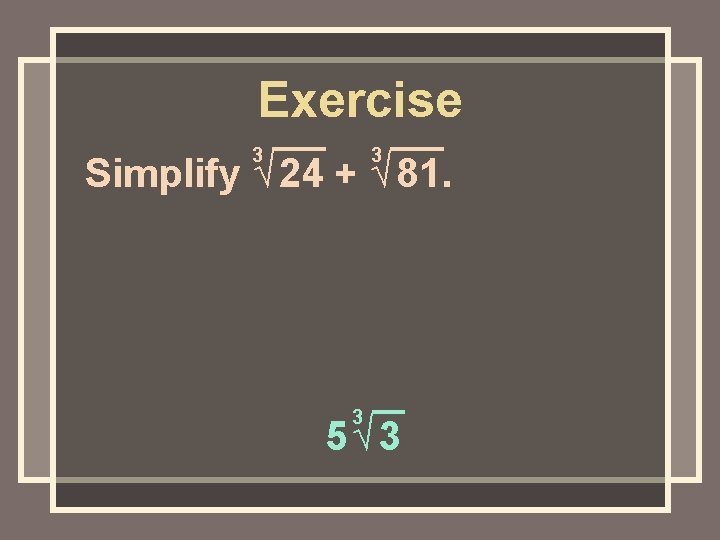
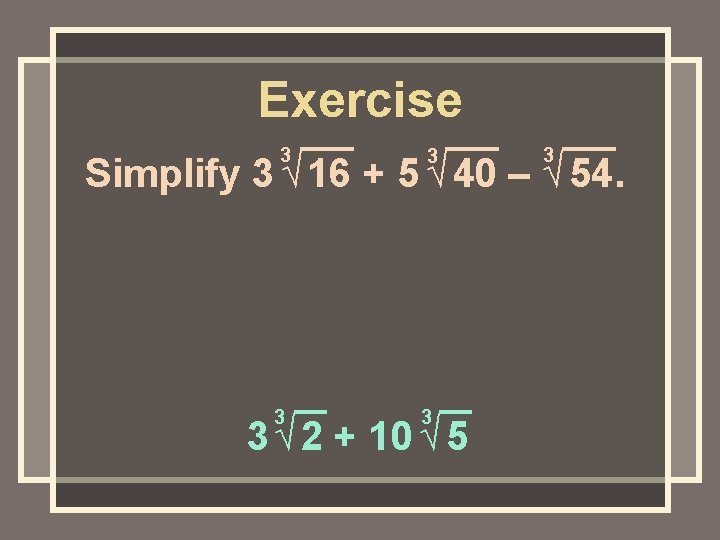
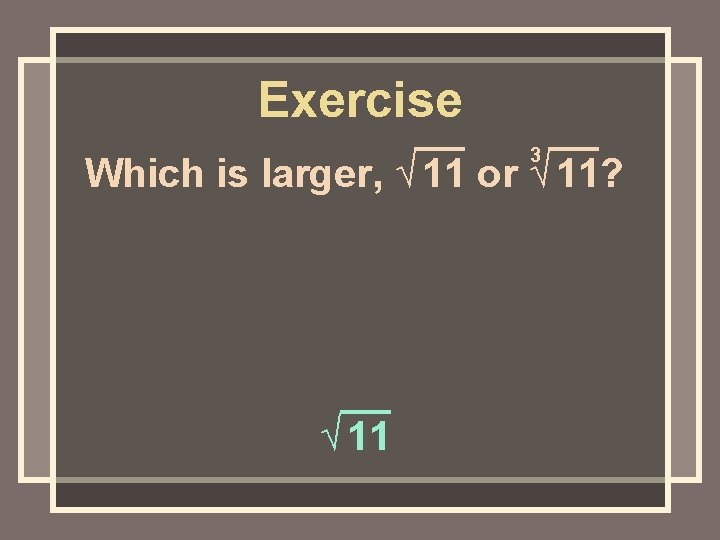
- Slides: 33
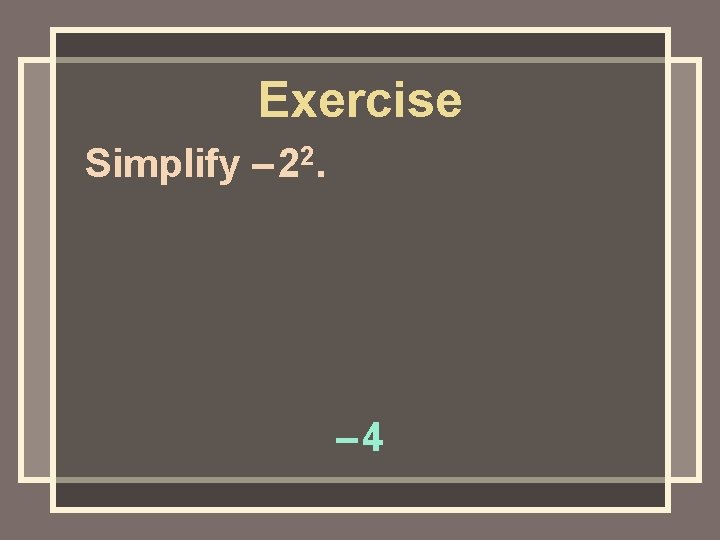
Exercise Simplify – 22. – 4

Exercise Simplify (– 2)2. 4
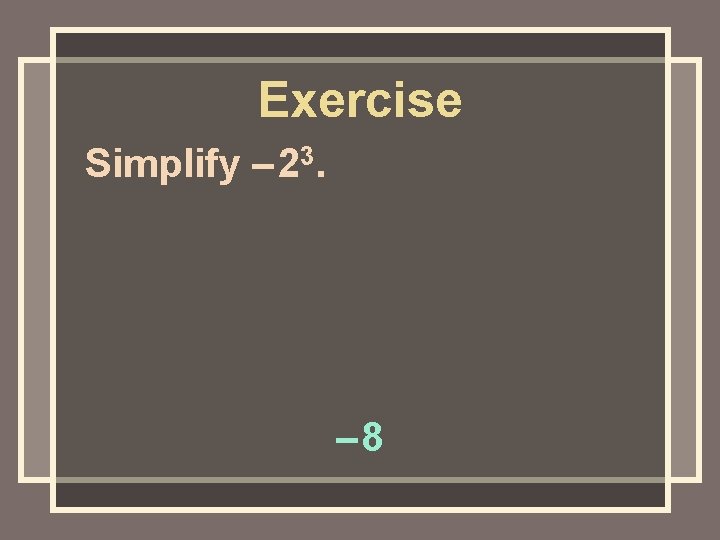
Exercise Simplify – 23. – 8
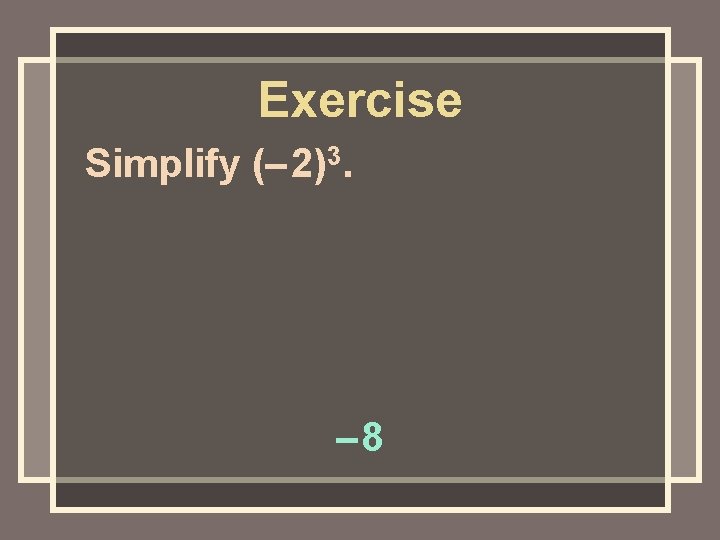
Exercise Simplify (– 2)3. – 8

Exercise Explain the difference between – x 2 and (– x)2. The negative sign is not taken to the power in the first expression, but it is in the second.

A positive real number has two square roots, one positive and one negative.

16 is a perfect square.

A number is a perfect cube if it is the result of cubing an integer.

8 is a perfect cube.

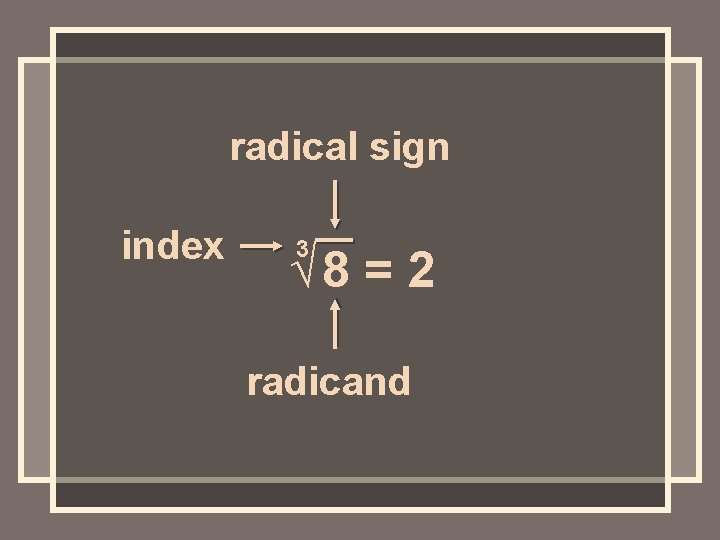
radical sign index 3 √ 8 = 2 radicand

Differences between Square Roots and Cube Roots of Real Numbers 1. Any real number has exactly one cube root. But any positive real number has two square roots, one positive and one negative.

Differences between Square Roots and Cube Roots of Real Numbers 2. The cube root of a negative number is a negative number. But there is no real square root of a negative number.
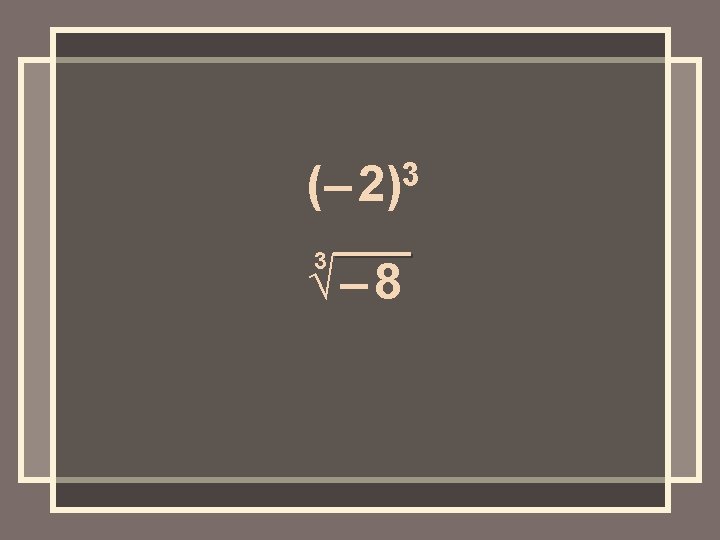

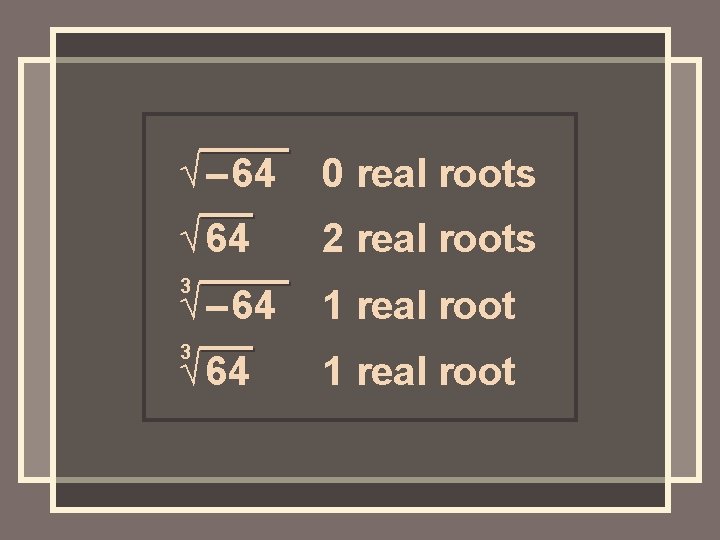
√ – 64 0 real roots √ 64 2 real roots 3 √ – 64 1 real root 3 1 real root √ 64

Example 1 3 Find √ 125. Since 53 = 125, the radical 3 √ 125 = 5.

Example 1 3 Find √ – 216. Since (– 6)3 = – 216, the 3 radical √ – 216 = – 6.

Example True or false: – 53 = (– 5)3 True

Example True or false: – 122 = (– 12)2 False

Example True or false: – 1331 = (– 13)31 True

Example 2 Find the consecutive 3 integers between which √ 70 lies. Use the < symbol to express your answers. 43 = 64 and 53 = 125. Since 70 lies between 64 and 125, 3 4 < √ 70 < 5.

Example 2 Find the consecutive 3 integers between which √ – 5 lies. Use the < symbol to express your answers. (– 1)3 = – 1 and (– 2)3 = – 8. Since – 5 lies between – 8 3 and – 1, – 2 < √ – 5 < – 1.

Example Between which two consecutive integers does 3 √ 12 lie? 2 and 3

Product Law for Roots For all a ≥ 0 and b ≥ 0 with n n ≥ 0, √ a • √ b = √ ab.
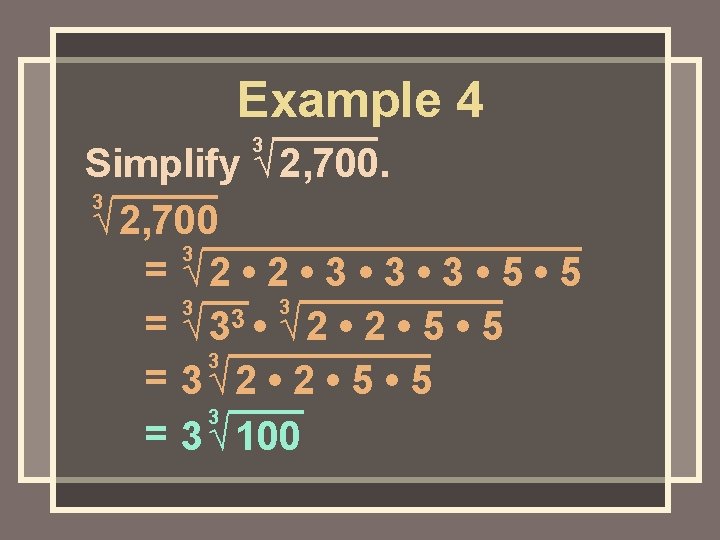
Example 4 3 Simplify √ 2, 700. 3 √ 2, 700 3 = √ 2 • 3 • 3 • 5 3 3 3 = √ 3 • √ 2 • 2 • 5 • 5 3 = 3 √ 100

Example 5 3 Simplify 7 √ 1, 080. 3 7 √ 1, 080 3 = 7√ 2 • 2 • 3 • 3 • 5 3 3 3 = 7√ 2 • √ 3 • √ 5 3 = 7 • 2 • 3√ 5 3 = 42 √ 5

Example 3 3 Simplify √ 432 and √ 50, 625. 3 3 6 √ 2; 15 √ 15

Example 3 3 Simplify √ 18 • √ 24. 3 6√ 2

Example 3 3 Simplify √ 135 – √ 40. 3 √ 5
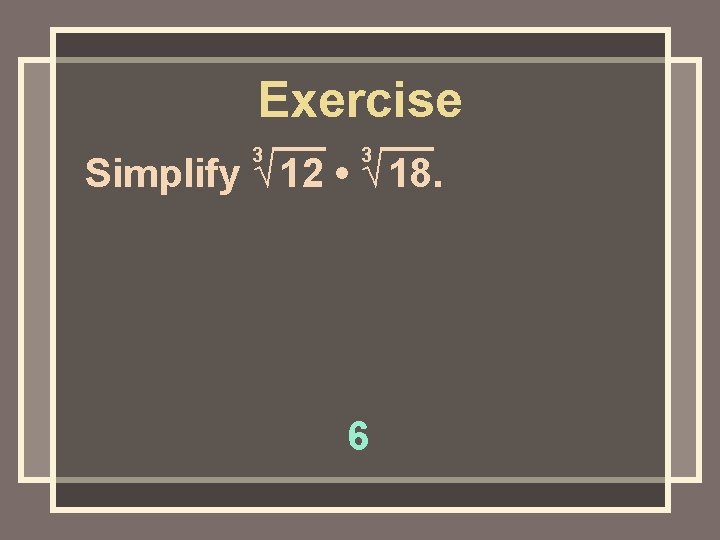
Exercise 3 3 Simplify √ 12 • √ 18. 6
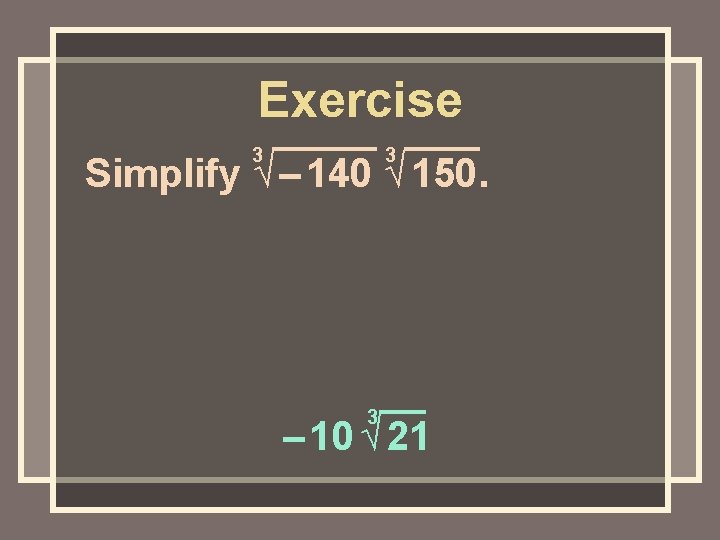
Exercise 3 3 Simplify √ – 140 √ 150. 3 – 10 √ 21
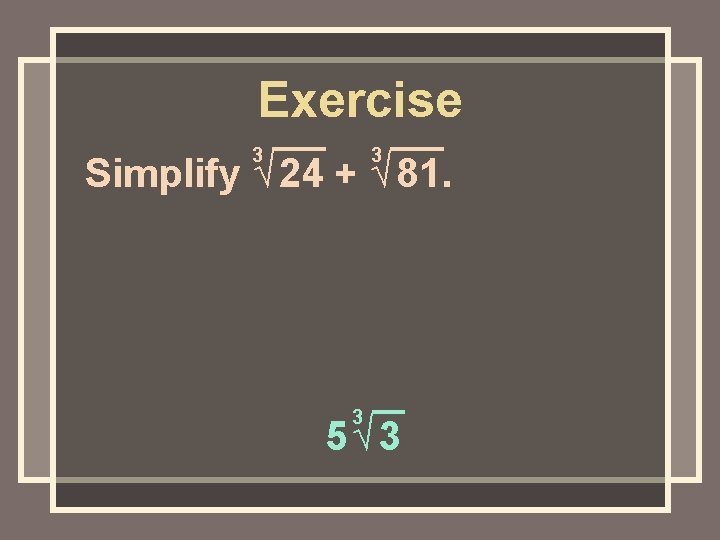
Exercise 3 3 Simplify √ 24 + √ 81. 3 5√ 3
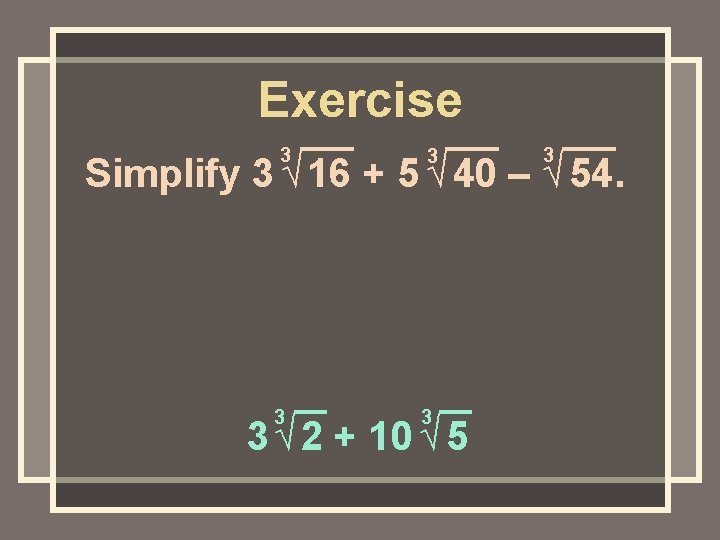
Exercise 3 3 3 Simplify 3 √ 16 + 5 √ 40 – √ 54. 3 √ 2 + 10 √ 5
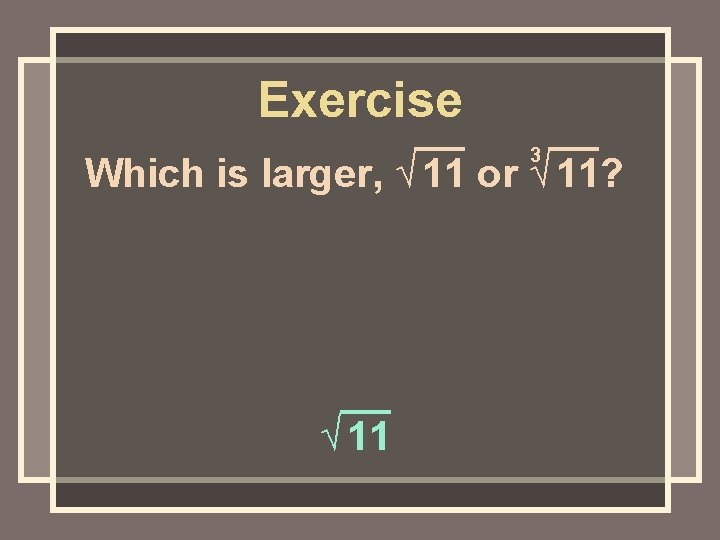
Exercise 3 Which is larger, √ 11 or √ 11? √ 11
 Simplify square root of 185
Simplify square root of 185 Simplify the expression
Simplify the expression Evaluate 32 8
Evaluate 32 8 Simplify radical 12
Simplify radical 12 How to simplify integer exponents
How to simplify integer exponents Log exponent rule
Log exponent rule Simplify compliance llc
Simplify compliance llc Lesson 4 work with algebraic expressions
Lesson 4 work with algebraic expressions How do you simplify a rational expression
How do you simplify a rational expression Useless production in automata
Useless production in automata Simplify each expression
Simplify each expression Remove the brackets and simplify questions
Remove the brackets and simplify questions How to simplify complex number fractions
How to simplify complex number fractions Dmca square root
Dmca square root How to simplify unions and intersections
How to simplify unions and intersections Evaluate square root of 150
Evaluate square root of 150 Distributive property
Distributive property Adding like terms
Adding like terms Simplify radical expressions using conjugates calculator
Simplify radical expressions using conjugates calculator Simplify this question
Simplify this question Factoring polynomials jeopardy
Factoring polynomials jeopardy Simplify integer exponents
Simplify integer exponents Simplify the following expression using k-map
Simplify the following expression using k-map Algebra 1 chapter 11
Algebra 1 chapter 11 Unit 7 review
Unit 7 review Simplify the following expression using k-map
Simplify the following expression using k-map Unit 7 lesson 2 simplify expressions
Unit 7 lesson 2 simplify expressions Simplify
Simplify Simplify complex numbers
Simplify complex numbers How to simplify expressions
How to simplify expressions 3xcxd
3xcxd How do you solve an inequality
How do you solve an inequality Expanding double brackets grid method
Expanding double brackets grid method How to simplify rates
How to simplify rates