Exercice 1 de gomtrie dans lespace sur les

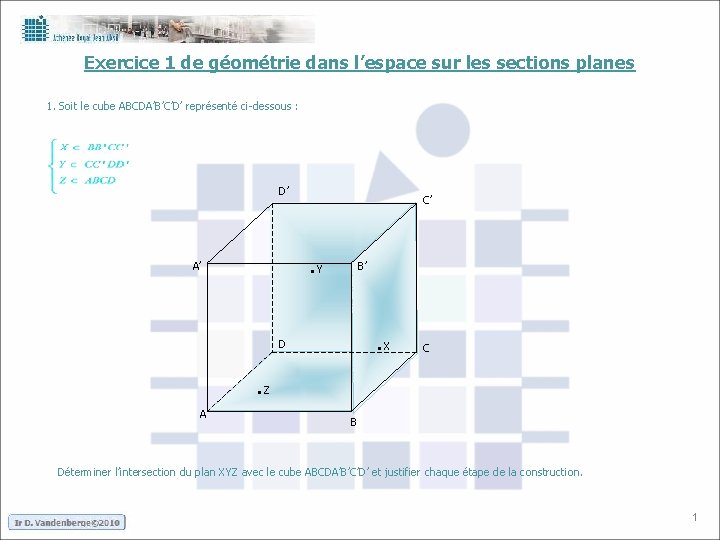
Exercice 1 de géométrie dans l’espace sur les sections planes 1. Soit le cube ABCDA’B’C’D’ représenté ci-dessous : D’ C’ . Y A’ B’ . X D C . Z A B Déterminer l’intersection du plan XYZ avec le cube ABCDA’B’C’D’ et justifier chaque étape de la construction. 1

2. On recherche l’intersection du plan XYZ avec les faces du cube ABCDA’B’C’D’. Les points X, Y et Z se trouvant sur des faces, on ne peut directement les relier car les droites XY, XZ et YZ transpercent le cube et ne se trouvent pas sur des faces. Une méthode consiste à déterminer le point de percée d’une de ces 3 droites dans la face du cube contenant l’autre point. On peut par exemple recher le point de percée (3) de la droite XY dans la face ABCD dans laquelle se trouve également Z. La droite 3 Z serait à l’intersection du plan XYZ et de la face inférieure du cube ABCD. Par conséquent, 3 Z serait la droite de la section plane recherchée dans la face inférieure ABCD du cube. 2

3. Pour trouver le point de percée (3) de la droite XY dans la face ABCD du cube, nous choisissons un plan contenant la droite XY et recherchons son intersection (1 2) avec la face ABCD. Cette droite 1 2 étant à la fois dans le plan XYZ et ABCD, coupe la droite XY au point 3 recherché. Nous utiliserons volontairement 2 méthodes pour la détermination du point 3. La méthode 1 choisit le plan C’XY, car l’intersection des plans contenant respectivement X et Y est l’arête CC’ et que seuls C’X et C’Y percent la face ABCD. La méthode 2 choisit le plan vertical comprenant X et Y, car son intersection avec la face ABCD est aisée. 3

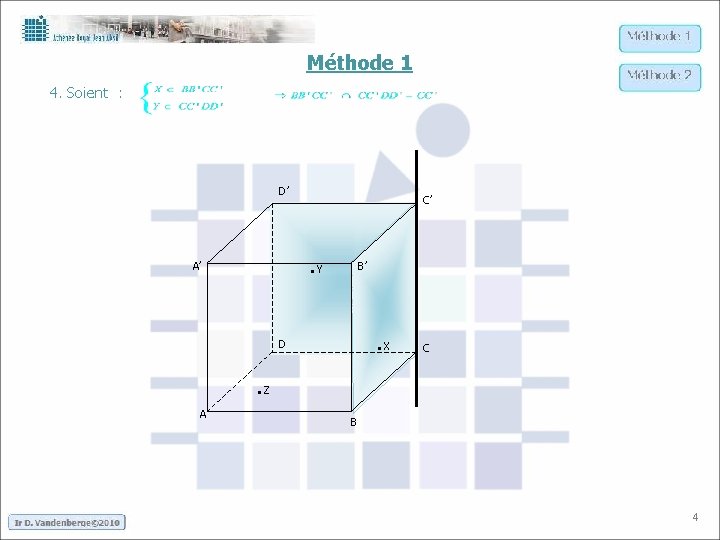
Méthode 1 4. Soient : D’ C’ . Y A’ B’ . X D C . Z A B 4

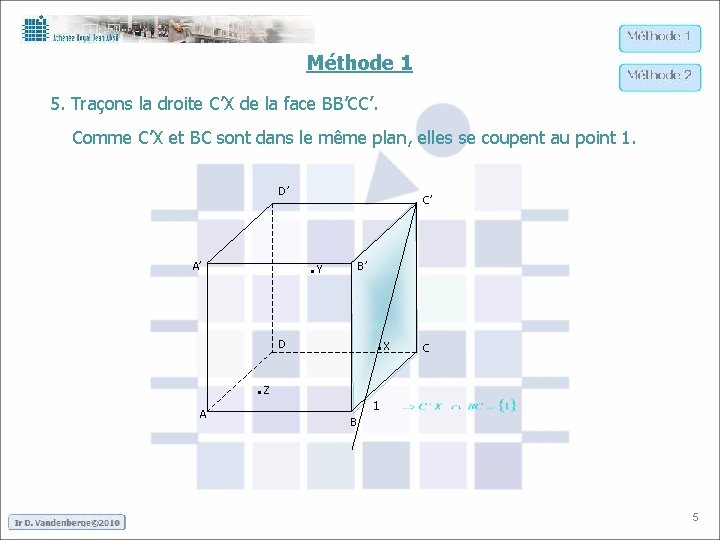
Méthode 1 5. Traçons la droite C’X de la face BB’CC’. Comme C’X et BC sont dans le même plan, elles se coupent au point 1. D’ C’ . Y A’ B’ . X D . Z A C 1 B 5

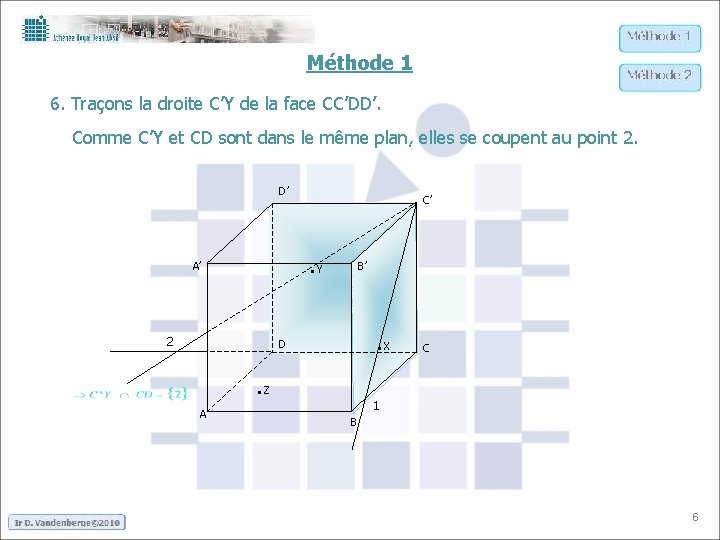
Méthode 1 6. Traçons la droite C’Y de la face CC’DD’. Comme C’Y et CD sont dans le même plan, elles se coupent au point 2. D’ C’ . Y A’ 2 B’ . X D . Z A C 1 B 6

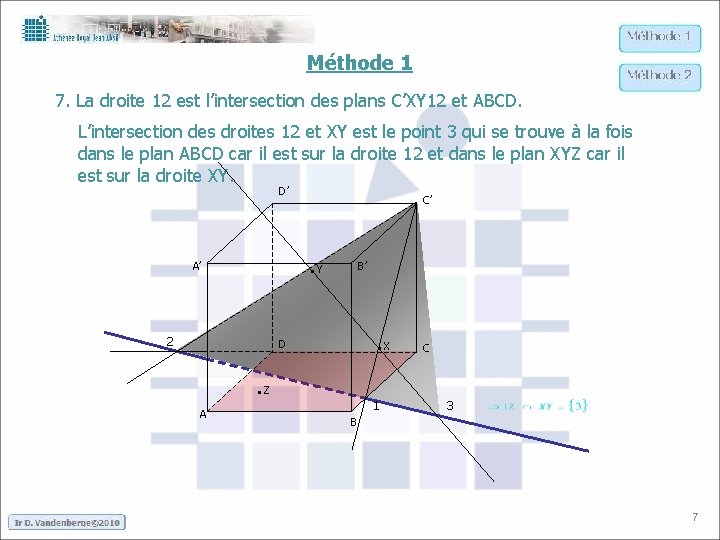
Méthode 1 7. La droite 12 est l’intersection des plans C’XY 12 et ABCD. L’intersection des droites 12 et XY est le point 3 qui se trouve à la fois dans le plan ABCD car il est sur la droite 12 et dans le plan XYZ car il est sur la droite XY. D’ C’ . Y A’ 2 B’ . X D . Z A 1 C 3 B 7

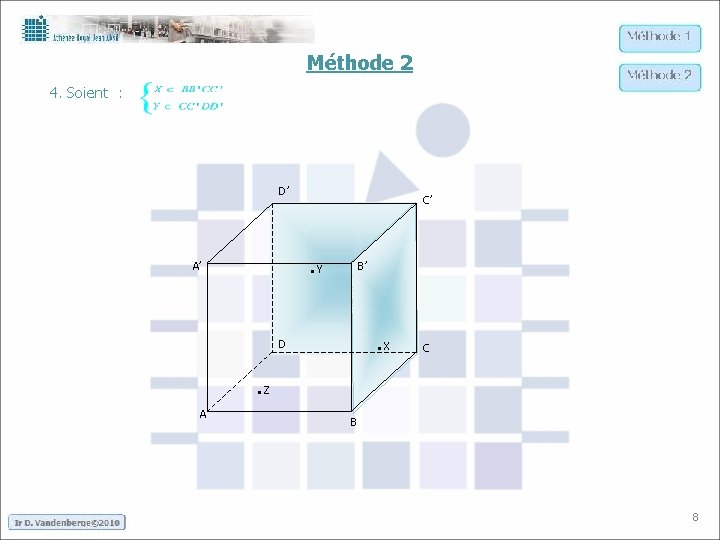
Méthode 2 4. Soient : D’ C’ . Y A’ B’ . X D C . Z A B 8

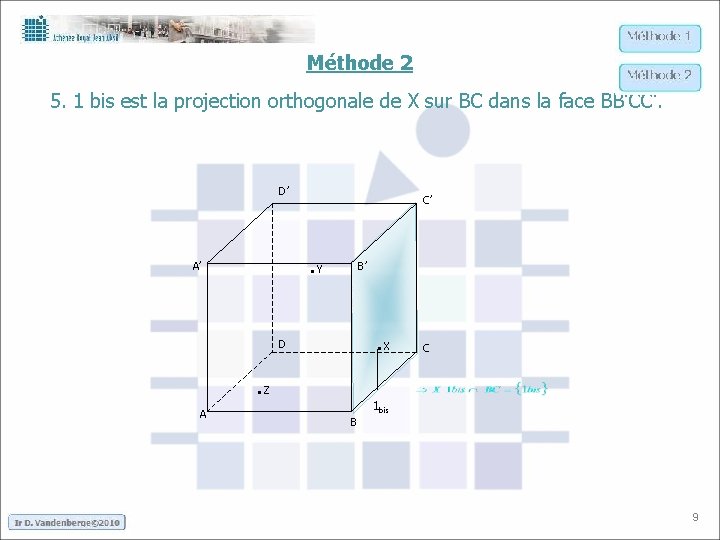
Méthode 2 5. 1 bis est la projection orthogonale de X sur BC dans la face BB’CC’. D’ C’ . Y A’ B’ . X D . Z A C 1 bis B 9

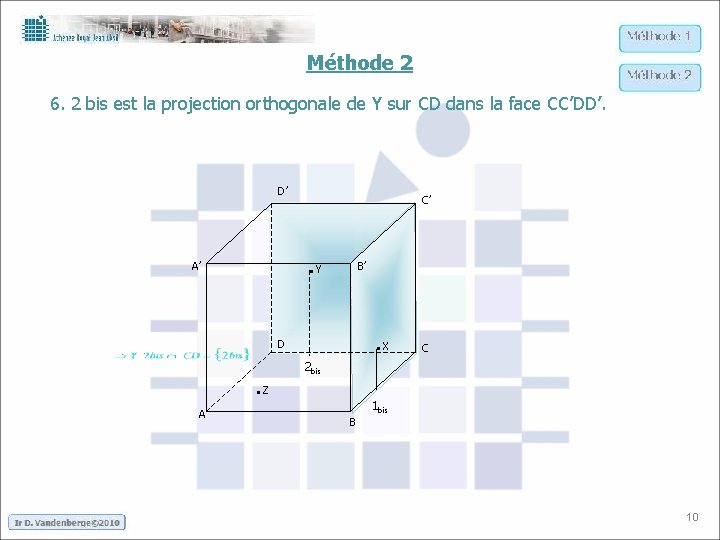
Méthode 2 6. 2 bis est la projection orthogonale de Y sur CD dans la face CC’DD’. D’ C’ . Y A’ B’ . X D C 2 bis . Z A 1 bis B 10

Méthode 2 7. La droite 1 bis 2 bis est l’intersection du plan vertical passant par X et Y et de la face ABCD. L’intersection des droites 1 bis 2 bis et XY est le point 3 qui se trouve à la fois dans le plan ABCD car il est sur la droite 12 et dans le plan XYZ car il est sur la droite XY. D’ C’ . Y A’ B’ . X D C 2 bis . Z A 1 bis 3 B 11

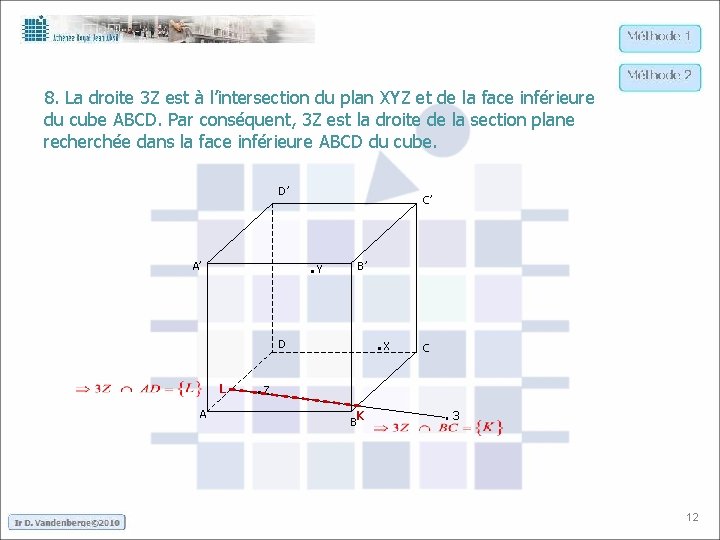
8. La droite 3 Z est à l’intersection du plan XYZ et de la face inférieure du cube ABCD. Par conséquent, 3 Z est la droite de la section plane recherchée dans la face inférieure ABCD du cube. D’ C’ . Y A’ B’ . X D L A C . Z K B . 3 12

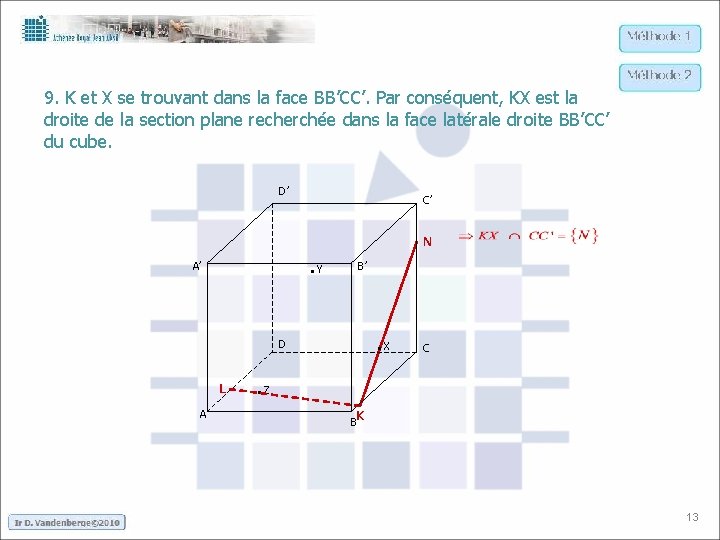
9. K et X se trouvant dans la face BB’CC’. Par conséquent, KX est la droite de la section plane recherchée dans la face latérale droite BB’CC’ du cube. D’ C’ N . Y A’ B’ . X D L A C . Z K B 13

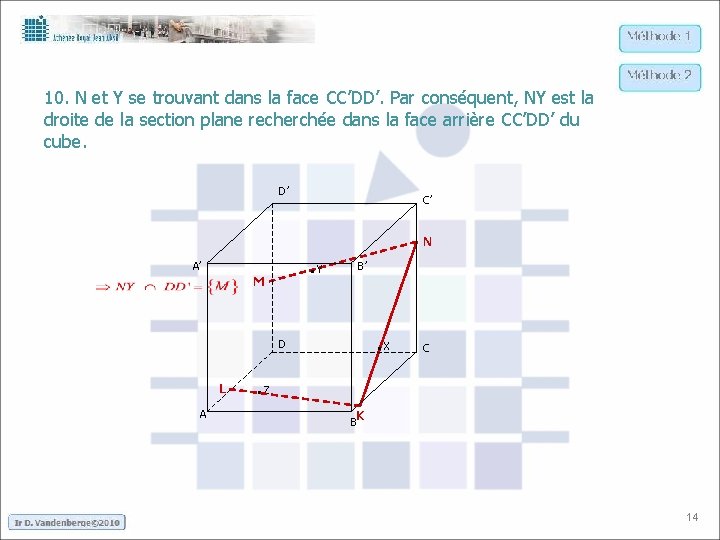
10. N et Y se trouvant dans la face CC’DD’. Par conséquent, NY est la droite de la section plane recherchée dans la face arrière CC’DD’ du cube. D’ C’ N . Y A’ M B’ . X D L A C . Z K B 14

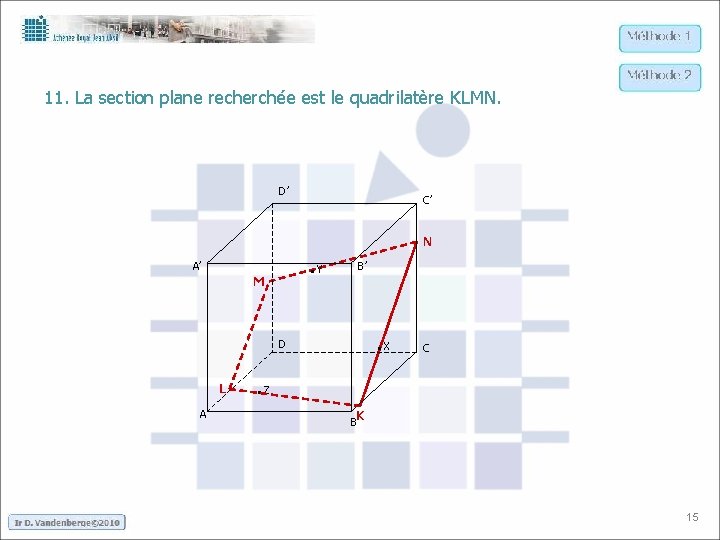
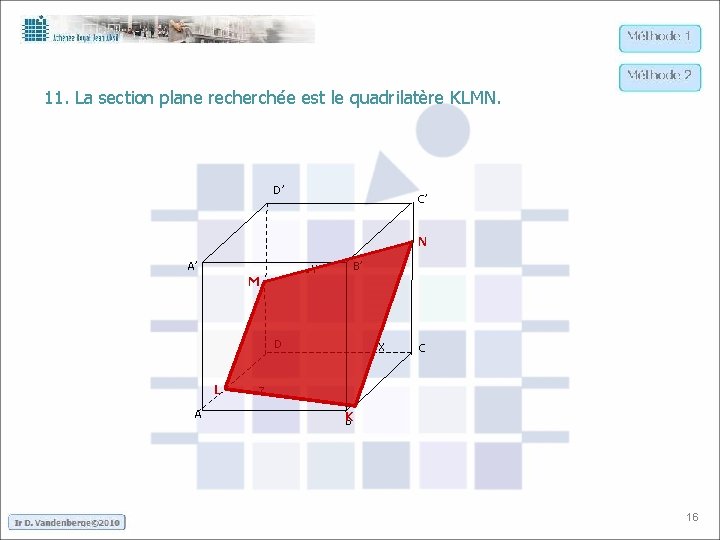
11. La section plane recherchée est le quadrilatère KLMN. D’ C’ N . Y A’ M B’ . X D L A C . Z K B 15

11. La section plane recherchée est le quadrilatère KLMN. D’ C’ N . Y A’ M B’ . X D L A C . Z K B 16