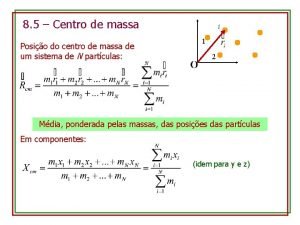
Esempio 1 Individuare il centro di massa di
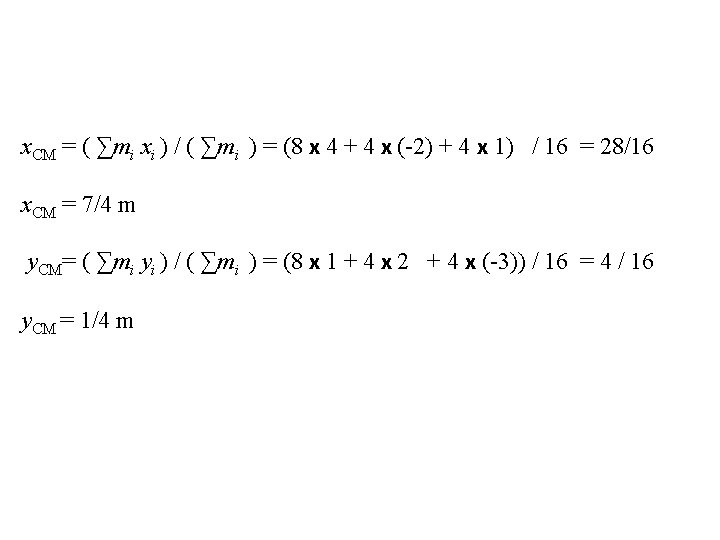







- Slides: 14

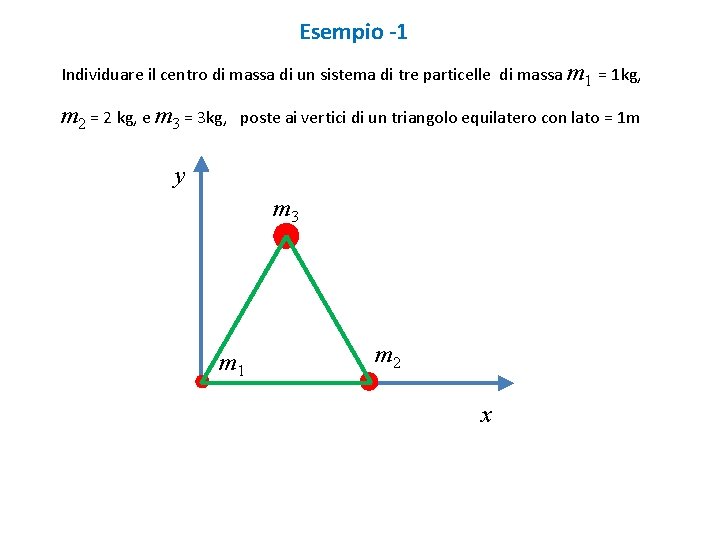
Esempio -1 Individuare il centro di massa di un sistema di tre particelle di massa m 1 = 1 kg, m 2 = 2 kg, e m 3 = 3 kg, poste ai vertici di un triangolo equilatero con lato = 1 m y m 3 m 1 m 2 x

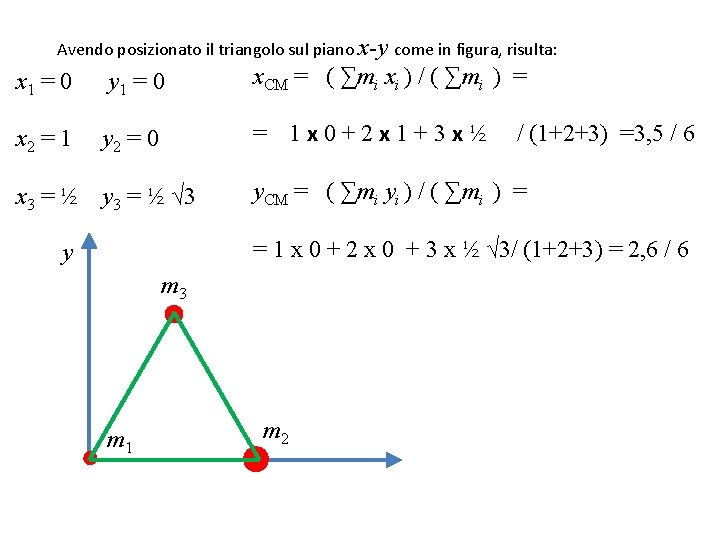
Avendo posizionato il triangolo sul piano x-y come in figura, risulta: x 1 = 0 y 1 = 0 x. CM = ( ∑mi xi ) / ( ∑mi ) = x 2 = 1 y 2 = 0 = 1 x 0+2 x 1+3 x½ x 3 = ½ y 3 = ½ √ 3 y. CM = ( ∑mi yi ) / ( ∑mi ) = / (1+2+3) =3, 5 / 6 = 1 x 0 + 2 x 0 + 3 x ½ √ 3/ (1+2+3) = 2, 6 / 6 y m 3 m 1 m 2

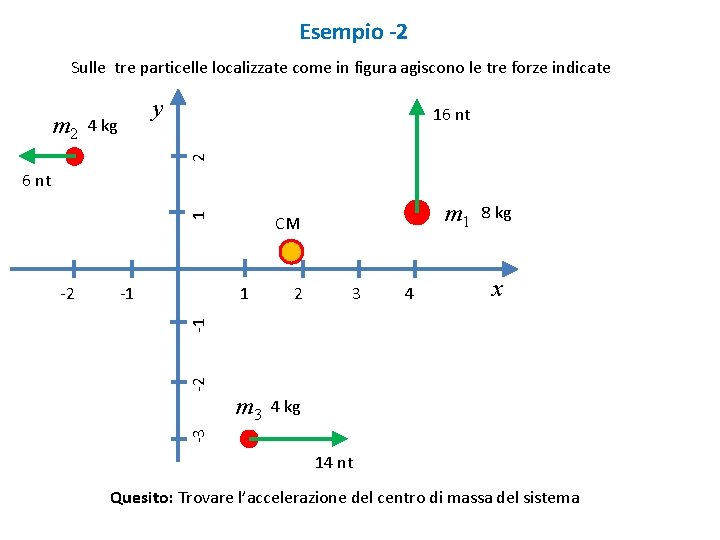
Esempio -2 Sulle tre particelle localizzate come in figura agiscono le tre forze indicate 4 kg 16 nt 2 m 2 y 1 6 nt 1 2 3 4 x -2 -1 -1 8 kg m 3 4 kg -3 -2 m 1 CM 14 nt Quesito: Trovare l’accelerazione del centro di massa del sistema
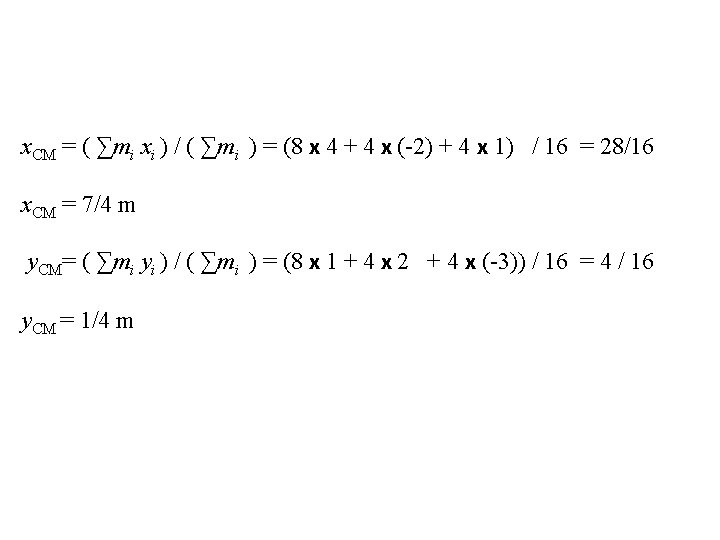
x. CM = ( ∑mi xi ) / ( ∑mi ) = (8 x 4 + 4 x (-2) + 4 x 1) / 16 = 28/16 x. CM = 7/4 m y. CM= ( ∑mi yi ) / ( ∑mi ) = (8 x 1 + 4 x 2 + 4 x (-3)) / 16 = 4 / 16 y. CM = 1/4 m

Determiniamo adesso la risultante delle forze agenti sul sistema: Fx = 0 – 6 nt + 14 nt = 8 nt Fy = 16 nt + 0 +0 = 16 nt La risultante delle forze ha pertanto modulo: F = (Fx 2 + Fy 2) ½ = (82 + 162) ½ = 18 nt E forma con l’asse x un angolo θ dato da θ = arctan (16 nt/8 nt) = arctan (2) = 63°

L’accelerazione del centro di massa sarà quindi a = F / Mtot = 18 nt / 16 kg = 1, 1 m/s 2 e formerà con l’asse x lo stesso angolo di 63 gradi

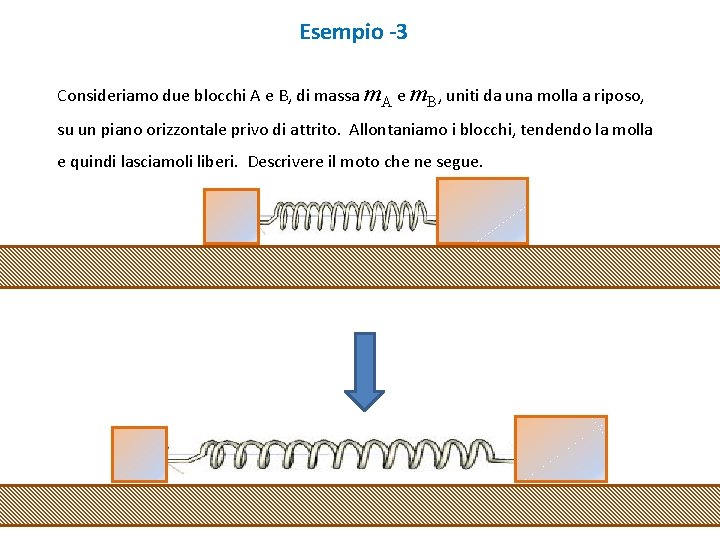
Esempio -3 Consideriamo due blocchi A e B, di massa m. A e m. B, uniti da una molla a riposo, su un piano orizzontale privo di attrito. Allontaniamo i blocchi, tendendo la molla e quindi lasciamoli liberi. Descrivere il moto che ne segue.

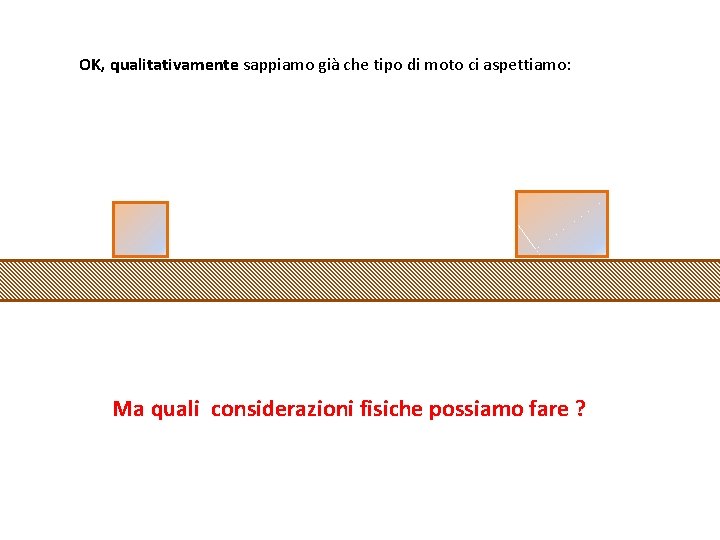
OK, qualitativamente sappiamo già che tipo di moto ci aspettiamo: Ma quali considerazioni fisiche possiamo fare ?

a) Il sistema è isolato b) Non agiscono forze esterne su di esso c) Le uniche forze presenti sono quelle interne generate dalla molla che si annullano a vicenda Applichiamo la legge di conservazione della quantità di moto: la quantità di moto di un sistema isolato si conserva Quando abbondoniamo i due blocchi, risulta P=0 Quindi deve essere P=0 in ogni istante successivo Questo certamente è possibile anche se i due blocchi si muovono: la quantità di moto è una grandezza vettoriale. Quindi se in un dato istante uno dei due blocchi avrà una quantità di moto positiva, l’altro l’avrà negativa. P = 0 = m. Av. A + m. Bv. B = − m. Av. A = −(m. B / m. A) v. B

Quindi: le velocità sono sempre di segno opposto e con il rapporto fra i moduli inverso al rapporto fra le masse L’energia cinetica di KA = ½ m. Av. A 2 A vale: che possiamo scrivere come: (m. Av. A)2 / 2 m. A che possiamo scrivere come: (m. Bv. B)2 / 2 m. B Analogamente: KB = ½ m. Bv. B 2 Da cui, poiché : (m. Av. A)2 = (m. Bv. B)2 risulta: K A / K B = m. B / m. A Cioè le energie cinetiche sono inversamente proporzionali alle rispettive masse Poiché l’energia meccanica si conserva, i blocchi continueranno a oscillare scambiando Continuamente energia cinetica e energia potenziale.

Esempio -4 Consideriamo il caso di una palla lanciata in aria e poi afferrata al rientro a terra. A scopo esemplificativo, assumeremo che l’agente che lancia la palla, essendo ancorato a terra faccia parte della terra. Considereremo anche trascurabile l’attrito dell’aria. Il sistema in esame in sostanza è il sistema terra- palla. Le forze in gioco fra i due elementi del sistema, e cioè la terra e la palla, sono solo forze interne. Definiremo un sistema di riferimento in cui la terra è inizialmente ferma, e rispetto al quale, al momento del lancio, subirà un contraccolpo.

Inizialmente, la quantità di moto del sistema terra-palla p. T-P è nulla, e poiché non vi sono forze esterne che agiscono sul sistema, resterà sempre nulla. Quindi in qualsiasi istante successivo: p. T-P = 0 = p. T + p. P 0 = m. T v. T + m. P v. P m. T v. T = − m. P v. P Quindi, quando la palla si allontana la terra retrocede e quando la palla si Riavvicina, la terra va in contro alla palla. I rapporto dei moduli delle velocità è inverso rispetto al rapporto fra le masse, il che ci dimostra che trascurare l’effetto del moto della Terra è lecito, essendo questo rapporto pari a circa 10− 24 !

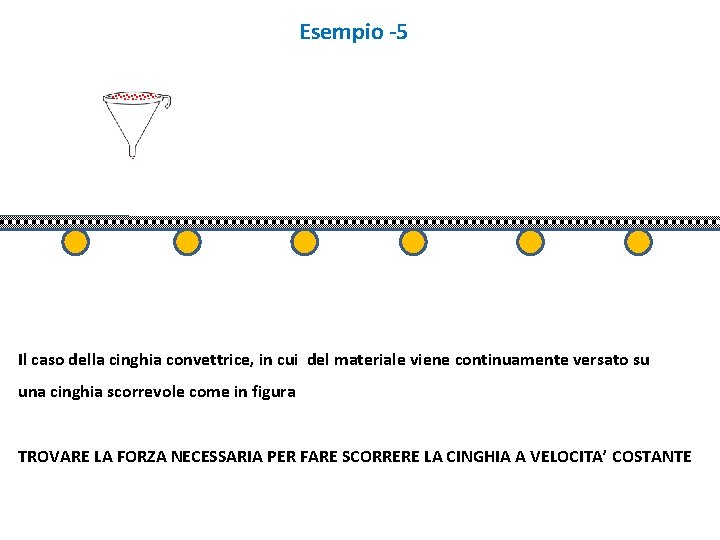
Esempio -5 Il caso della cinghia convettrice, in cui del materiale viene continuamente versato su una cinghia scorrevole come in figura TROVARE LA FORZA NECESSARIA PER FARE SCORRERE LA CINGHIA A VELOCITA’ COSTANTE

Indichiamo con m la massa del materiale sulla cinghia e M la massa della cinghia. La quantità di moto del sistema (cinghia + materiale sulla cinghia) sarà: P = (m + M) v e la forza che cerchiamo è F = d. P/dt Cioè: F = d/dt [ (m+M) v ] = (m+M) dv/dt + v d/dt (m+M) = (m+M) dv/dt + v dm/dt + v d. M/dt Poiché M e v sono costanti l’equazione si riduce a: F = v dm/dt
 I quasi incidenti sono facili da individuare
I quasi incidenti sono facili da individuare Struttura di un tema argomentativo
Struttura di un tema argomentativo Cz norte centro historico
Cz norte centro historico Energia cinetica do centro de massa
Energia cinetica do centro de massa Centro de massa corpo humano
Centro de massa corpo humano Centro da massa
Centro da massa Centro di massa
Centro di massa Rapporto massa grassa massa magra
Rapporto massa grassa massa magra Numero di avogadro formula
Numero di avogadro formula Massa lamina
Massa lamina Composizione percentuale
Composizione percentuale Solu.zone chimica molecole in movimento
Solu.zone chimica molecole in movimento Massa molar formula
Massa molar formula Rapporto massa grassa massa magra
Rapporto massa grassa massa magra Scheda misure antropometriche
Scheda misure antropometriche