Electrostatics 1 The equations of Electrostatics Steady state

Electrostatics 1. The equations of Electrostatics Steady state • the electromagnetic field quantities do not vary with respect to time ( ) and there are no energy transformations from electromagnetic form into other forms. Electromagntic induction law: Electric flux law: with local form: (1) with local form: (2) Connection law between D and E, for linear media, for example. (3) U N K N O W N S If we add the well-formulated boundary conditions => the electric field (D, E) is uniquely determined. ÞWe can study the electric component (D, E) of the electromagnetic field, independent from the magnetic component (B, H). (*) That part of electromagnetics that studies this (*) is called ELECTROSTATICS.

Electrostatica 1. The equations of Electrostatics Electric Potential Under conditions given in (1), the electric potential theorem is valid: there exists an electric potential V defined by the relation: (4) - P 0 is a point with an arbitrary, fixed, reference potential; - the integral takes place for any path from P 0 to P; (5) with the local form: By replacing (5) in (3) and then in (2)=> (6) Remark (1) (2) (3)

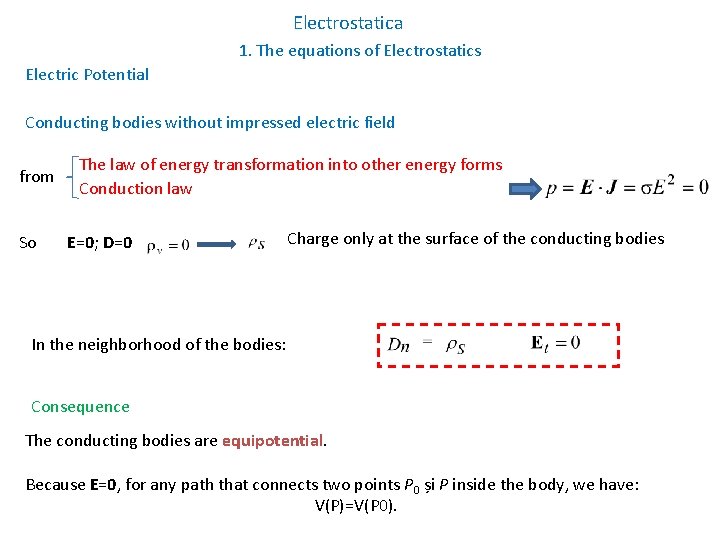
Electrostatica 1. The equations of Electrostatics Electric Potential Conducting bodies without impressed electric field from So The law of energy transformation into other energy forms Conduction law E=0; D=0 Charge only at the surface of the conducting bodies In the neighborhood of the bodies: Consequence The conducting bodies are equipotential. Because E=0, for any path that connects two points P 0 și P inside the body, we have: V(P)=V(P 0).

Electrostatica 1. The equations of Electrostatics ; Uniqueness Theorem In Annex B, is formulated and demonstrated a general theorem for steady state. As follows, we present a consequence of this theorem, very useful for the electrostatics problems that we’ll discuss. An interior with conducting wall (it can also be the surface from infinity) => is equipotential and we’ll take on it the reference potential equal to zero (sometimes: is “the grounding”). Inside we have n conducting bodies (n=3), which are also echipotential. For the media around the conductors, we know the connection law between D and E, (linear) and the volume density of the electric charge. The electric field (D, E) (described by the equations (1), (2), (3)) is uniquely determined if the followings are given: a) the electric charges of the conducting bodies b) the electric potentials of the conducting bodies Remark. The uniqueness theorem is valid also if the media inside is nonlinear, but with dissipative characteristics D=f(E), for any E’ E”. All media types belongs to this category, excepting media with hysteresis.

Electrostatics 1. The equations of Electrostatics Superposition Theorem If we assume the medium inside is linear (3). To electric charges corresponds a unique electric field (D’, E’) To electric charges corresponds a unique electric field (D”, E”) Then, to the charges corresponds a unique electric field The superposition theorems results immediately from the linearity of equations (1), (2), (3) and from the uniqueness theorem. The electric field form theorem verifies the equations (1), (2), (3) and is unique.

Electrostatics 2. THE RELATIONS BETWEEN THE CHARGES AND THE POTENTIALS OF A SYSTEM of CONDUCTING BODIES (MAXWELL). CAPACITORS - an interior with a conducting wall in which we have n conducting bodies (n=3); - the medium around the conducting bodies is linear and If the charges of the conducting bodies are given, then it results the unique electric field (D, E) and, as a consequence, the potentials To the values correspond the potentials denoted by Then, form the superposition theorem, it results that: for the electric charges: we have the potentials: OR: The FIRST form of the relations between charges and potentials of a system of conducting bodies. (2. 1)

Electrostatics 2. THE RELATIONS BETWEEN THE CHARGES AND THE POTENTIALS OF A SYSTEM of CONDUCTING BODIES (MAXWELL). CAPACITORS In matrix form, relations (2. 1) can be written: (2. 1’) Are called poential coeffiecients Remark: is symmetric Is positively defined for any matrix Then, it is invertible and we obtain: (2. 2) (2. 2’) OR: The SECOND form of the relations between charges and potentials of a system of conducting bodies. - are the influence coefficients; their matrix is symmetric and positively defined

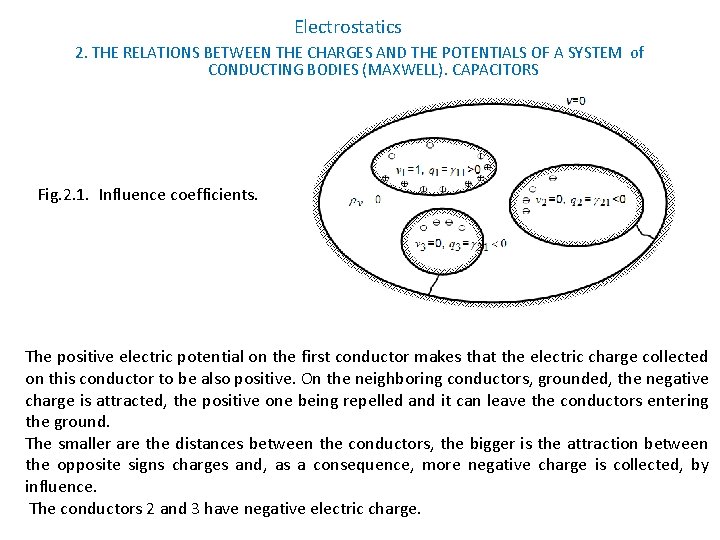
Electrostatics 2. THE RELATIONS BETWEEN THE CHARGES AND THE POTENTIALS OF A SYSTEM of CONDUCTING BODIES (MAXWELL). CAPACITORS Fig. 2. 1. Influence coefficients. The positive electric potential on the first conductor makes that the electric charge collected on this conductor to be also positive. On the neighboring conductors, grounded, the negative charge is attracted, the positive one being repelled and it can leave the conductors entering the ground. The smaller are the distances between the conductors, the bigger is the attraction between the opposite signs charges and, as a consequence, more negative charge is collected, by influence. The conductors 2 and 3 have negative electric charge.

Electrostatics 2. THE RELATIONS BETWEEN THE CHARGES AND THE POTENTIALS OF A SYSTEM of CONDUCTING BODIES (MAXWELL). CAPACITORS In the first part of relations given in (2. 2) we do replace: We make the following notations: We obtain the relation Proceeding in a similar manner (2. 3) The THIRD form of the relations between charges and potentials of a system of conducting bodies.

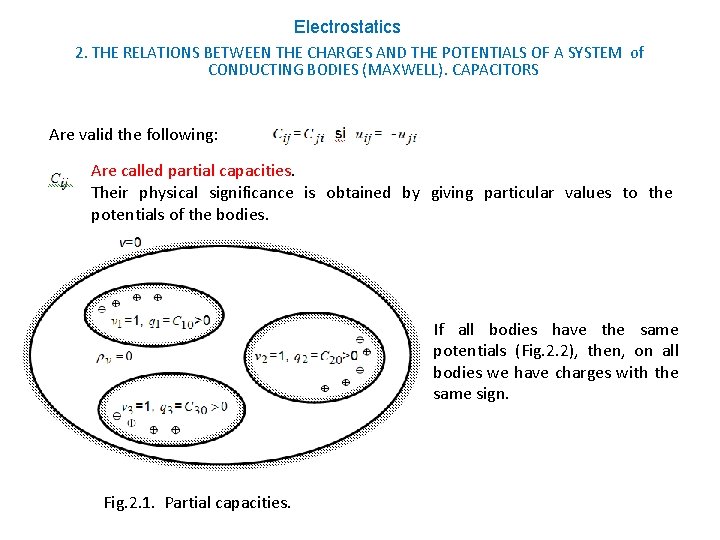
Electrostatics 2. THE RELATIONS BETWEEN THE CHARGES AND THE POTENTIALS OF A SYSTEM of CONDUCTING BODIES (MAXWELL). CAPACITORS Are valid the following: Are called partial capacities. Their physical significance is obtained by giving particular values to the potentials of the bodies. If all bodies have the same potentials (Fig. 2. 2), then, on all bodies we have charges with the same sign. Fig. 2. 1. Partial capacities.

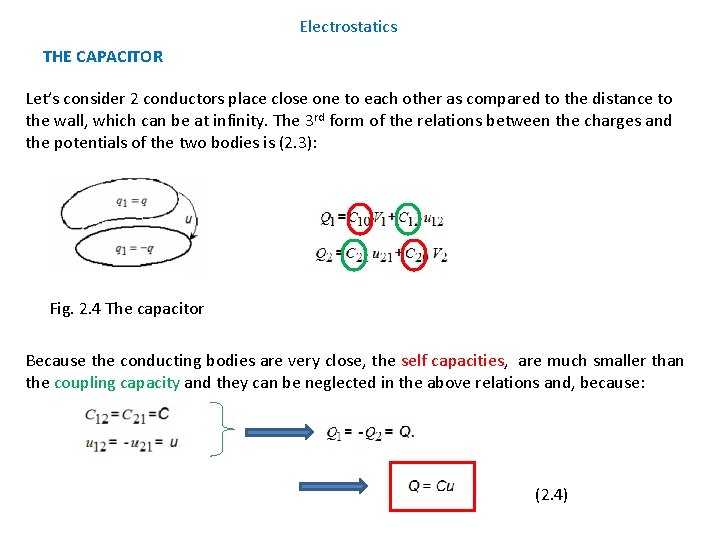
Electrostatics THE CAPACITOR Let’s consider 2 conductors place close one to each other as compared to the distance to the wall, which can be at infinity. The 3 rd form of the relations between the charges and the potentials of the two bodies is (2. 3): Fig. 2. 4 The capacitor Because the conducting bodies are very close, the self capacities, are much smaller than the coupling capacity and they can be neglected in the above relations and, because: (2. 4)

Electrostatics THE CAPACITOR (2. 4) We call capacitor a system consisting of two conducting bodies (called armatures) which have the property that their charges are equal as magnitude but of opposite signs. The constant C from relation (2. 4) the capacity of the capacitor. The unit of measure of the capacity is the Farad (F), which, unfortunately, from the technical point of view is huge. For this reason, very often, the sub-multiples are used: : Fig. 2. 5 The symbol of the capacitor

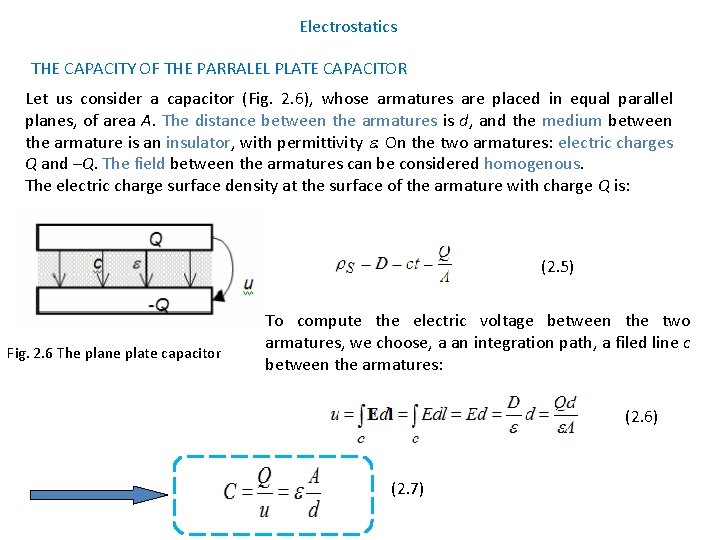
Electrostatics THE CAPACITY OF THE PARRALEL PLATE CAPACITOR Let us consider a capacitor (Fig. 2. 6), whose armatures are placed in equal parallel planes, of area A. The distance between the armatures is d, and the medium between the armature is an insulator, with permittivity . On the two armatures: electric charges Q and –Q. The field between the armatures can be considered homogenous. The electric charge surface density at the surface of the armature with charge Q is: (2. 5) Fig. 2. 6 The plane plate capacitor To compute the electric voltage between the two armatures, we choose, a an integration path, a filed line c between the armatures: (2. 6) (2. 7)

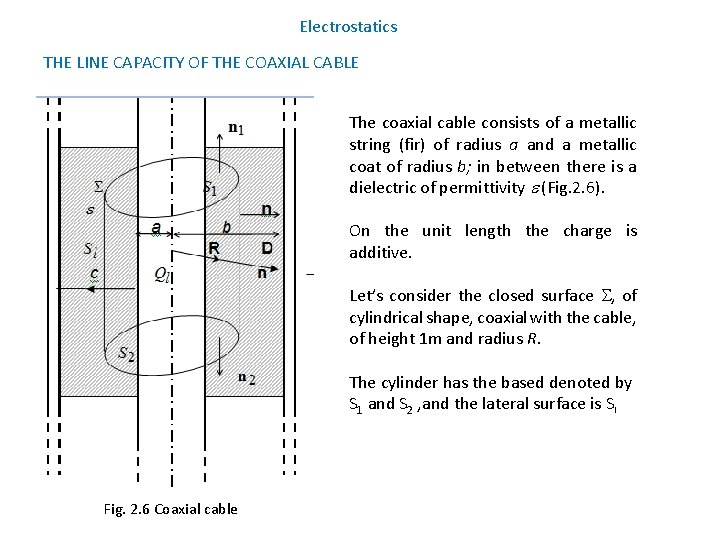
Electrostatics THE LINE CAPACITY OF THE COAXIAL CABLE The coaxial cable consists of a metallic string (fir) of radius a and a metallic coat of radius b; in between there is a dielectric of permittivity (Fig. 2. 6). On the unit length the charge is additive. Let’s consider the closed surface , of cylindrical shape, coaxial with the cable, of height 1 m and radius R. The cylinder has the based denoted by S 1 and S 2 , and the lateral surface is Sl Fig. 2. 6 Coaxial cable

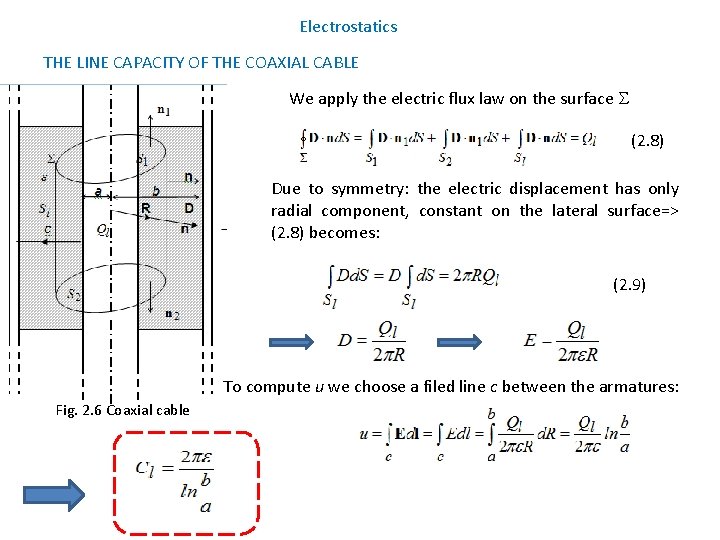
Electrostatics THE LINE CAPACITY OF THE COAXIAL CABLE We apply the electric flux law on the surface (2. 8) Due to symmetry: the electric displacement has only radial component, constant on the lateral surface=> (2. 8) becomes: (2. 9) To compute u we choose a filed line c between the armatures: Fig. 2. 6 Coaxial cable

Electrostatics u-i relationship at the capacitor’s terminals We assume that the electric charge on the capacitor’s armatures is due to the currents (Fig. 2. 7). By applying the electric charge conservation theorem o the closed surface that surrounds the armatures, passing through the insulating medium between the armatures, it results: and Fig. 2. 7 The current of the capacitor Linear capacitor The system consisting of conducting bodies and assuming that if we use the currents to power the system the electric charges will increase, then by applying the electric charge conservation theorem on the surface of the 1 st body:

Electrostatics Networks of capacitors are electric circuits consisting only of capacitors and voltage sources. From electric circuits theory point of view, the networks of capacitors have excess elements: there are loops consisting only capacitors and voltage sources. Therefore, they are circuit models for which the existence of the solution (u, i) is not ensured in the functions domain. Anyway, we’ll see that in static regime one can determine a solution (u, Q): The second Kirchhoff’s theorem for a network of capacitors. The second Kirchhoff’s theorem for electric circuits is valid also for networks of capacitors: the sum of the voltages corresponding to the branches in a loop is zero: (2. 14) The first Kirchhoff’s theorem for a network of capacitors. Let’s consider a node (section) of capacitors and let be a surface that passes through the insulating medium between the armatures (Fig. 2. 8). Applying the charge conservation theorem on the surface : Fig. 2. 8. Node of capacitors

Electrostatics Networks of capacitors obtained from the network of capacitors evolution (2. 15) The computation of the network of capacitors is done by adding to Kirchhoff’s relations (2. 14) and (2. 15) the values of the voltages from the voltage sources terminals and the relations between the voltages and the charges of the capacitors (2. 4). The resistive circuits computation procedures can be used. Example. The capacitor with capacity C 1 is charge with the electric charge Q 0 , and the capacitor C 2 is discharged, the switch k being open. At t=0, the switch is closed, by placing in parallel the two capacitors. Find the capacitors charges and the voltages at t>0. TKII When k is closed, the electric charge initially placed only on the armatures of the capacitor C 1 is redistributed on the armatures of the both capacitors.

Electrostatics Parallel connection of the capacitors Let’s consider n capacitors placed as in Fig. 2. 11. We obtain an equivalent capacitor with the equivalent capacity: Proof Fig. 2. 11 parallel connection Remarks: a) The equivalent capacity is much bigger than any of the capacities that form the system. b) If the capacities placed in parallel are equal to C, the equivalent capacity is: