El Azar un recorrido desde la Antigedad a


























- Slides: 37

El Azar: un recorrido desde la Antigüedad a la Época Actual Servet Martínez CMM-DIM- U. de CHILE Núcleo Milenio Información y Aleatoriedad http: //www. dim. uchile. cl/~random/ Preparación: Mª Inés Rivera Conferencia ICM Gran Público Fundación Telefónica 24/09/03 1

PREHISTORIA • Los Juegos de azar pueden haber sido una de las primeras invenciones del ser humano viviendo en sociedad. • Se especula que desde los tiempos del neolítico habrían huesos tallados que permiten obtener resultados equilibrados (como en los dados), y que no serían herramientas “útiles”, solo servirían para jugar (¿adivinación? ). HISTORIA • En tiempo de los egipcios ya se producen dados muy bien pulidos y equilibrados. 2

UNA HISTORIA Una historia sorprendente aparece en el gran relato épico indio Mahábharata: es la historia de Nala. Kali, un semidiós se enfurece cuando Nala gana en un juego de dados la mano de una princesa, y en castigo Kali toma posesión del cuerpo y alma de Nala y en una apuesta Nala pierde su reino y vaga demente por años. Posteriormente trabaja para un potentado, Rtuparna, quien queda admirado de que Nala sepa estimar el número de hojas y frutos de un árbol, tan sólo examinando una pequeña parte. El lo ayuda a recuperar su reino, lo que consigue Nala en un nuevo juego de dados. El relacionar las apuestas con la estimación no se haría en Europa sino a partir del siglo XVII. 3 *Ian Hacking, The Emergence of Probability, Cambridge U. P. 1975

PARADOJAS Dilema del Prisionero O A B Uno de los tres prisioneros será condenado a muerte y los otros dos serán liberados. 4

0 A B Caso 1 M L L Caso 2 L M L Caso 3 L L M Probabilidad (0 Muere)=1/3 Información: Un guardia le dice a 0 que B se salva. ¿Cual es la Probabilidad que 0 muera? 5

La selección del guardia, que llamaremos Y se hace así: Y=B si A muere Y=A si B muere Si A y B se salvan se tira una moneda y se elige A ó B con probabilidad 1/2. Luego Probabilidad {Y=B}=1/2 Prob {0 muere, Y=B}= Prob {0 muere} Prob {Y=B / 0 muera} = Prob {0 muere} Prob{Y=B} Deducción: Probabilidad {0 muera / Y=B} = Probabilidad {0 muera}=1/3 Probabilidad {A muera / Y=B} = 2/3 Luego a 0 no le conviene intercambiar su suerte con A. 6

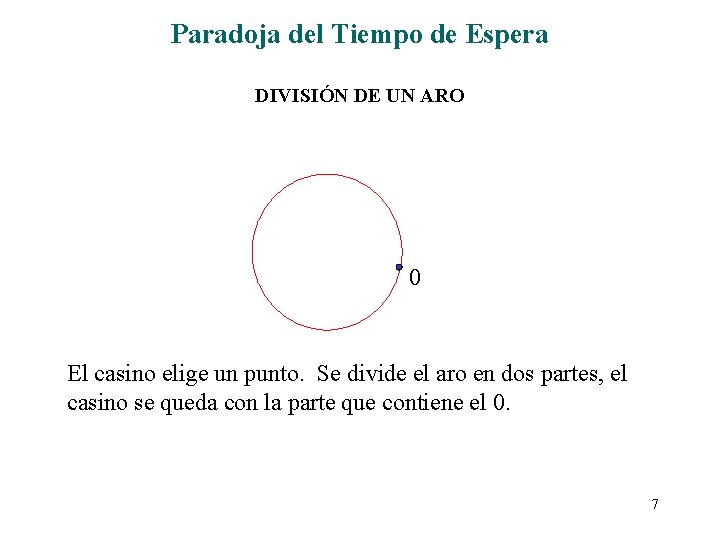
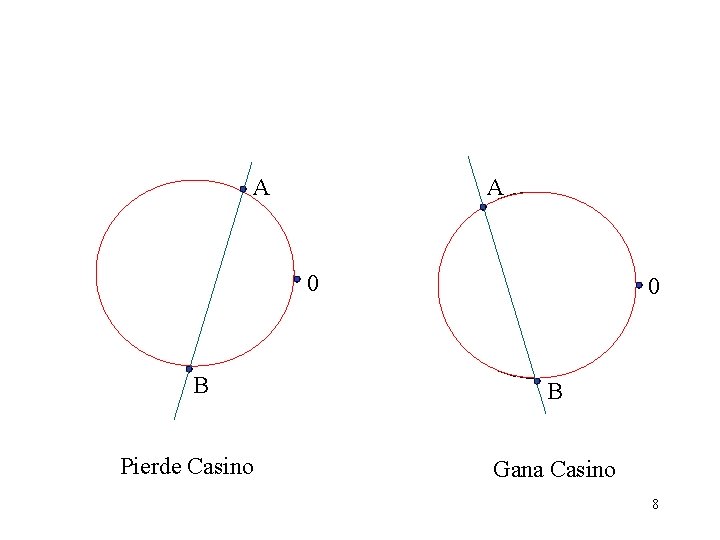
Paradoja del Tiempo de Espera DIVISIÓN DE UN ARO 0 El casino elige un punto. Se divide el aro en dos partes, el casino se queda con la parte que contiene el 0. 7

A A 0 B Pierde Casino 0 B Gana Casino 8

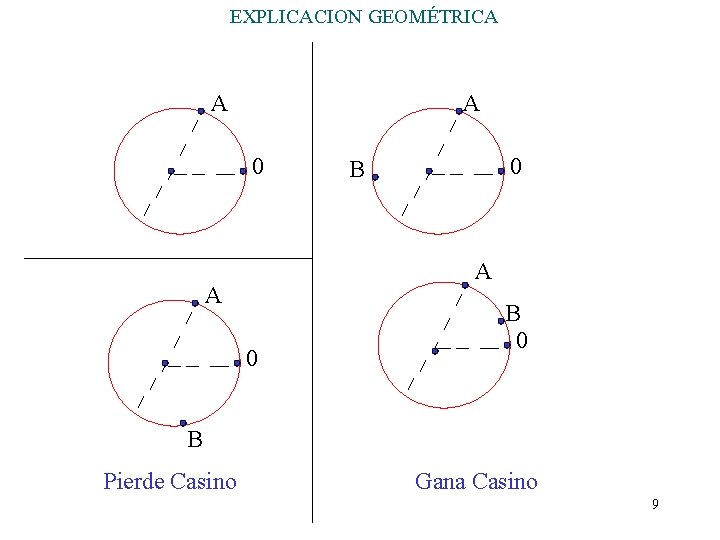
EXPLICACION GEOMÉTRICA A A 0 0 B A A 0 B Pierde Casino Gana Casino 9

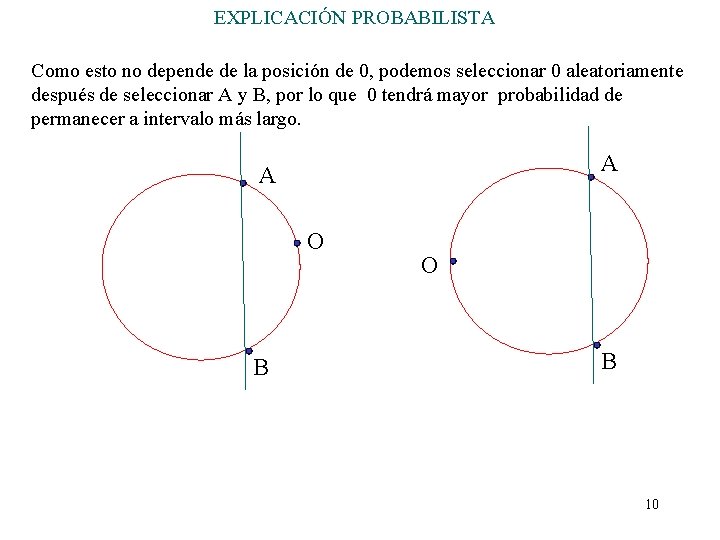
EXPLICACIÓN PROBABILISTA Como esto no depende de la posición de 0, podemos seleccionar 0 aleatoriamente después de seleccionar A y B, por lo que 0 tendrá mayor probabilidad de permanecer a intervalo más largo. A A O B 10

Paradoja de San Peterburgo El Casino paga 2 n si sale cara por primera vez en la n-ésima tirada. ¿Cuánto esta dispuesto a pagar el jugador por entrar al juego? Sea X la ganancia. Su valor esperado, o media teórica, es: (pues la probabilidad de que salga cara por primera vez en la n-ésima tirada es: 1/2 n ) Sin embargo el jugador esta en general dispuesto a pagar una cantidad modesta, que depende de su propensión al riesgo. 11

CALCULOS PREVIOS Antes de Pascal habían problemas para evaluar combinatorias simples de dados. Por ejemplo en juegos a 3 dados se discutía la frecuencia del 10 y el 12. 12 651 6 + 10 631 6 + 642 6 622 3 633 + 3 552 + 541 + 6 3 543 + + 6 4 4 4 = 5 Combinaciones 6 + 532 442 + 3 Galileo Galilei 1564 -1642 1 = 24 Permutaciones 433 = 5 Combinaciones + 3 = 27 Permutaciones Citemos como anécdota que Galileo dio respuesta correcta a éste y otros juegos, confirmando lo que ya era experiencia. 12

SIGLOS XVII, XVIII: GRANDES NÚMEROS Apuestas sobre duración de vida de grandes personajes. Resolución de problemas prácticos ligadas a tablas de mortalidad. Esperanza de vida: seguros. En general si Xn son variables independientes con igual ley se cumple la ley de grandes números E(X)=Esperanza de X o media Teórica. 13

TEOREMA DE LOS GRANDES NÚMEROS Xn independientes Xn =1 con proba p Xn = 0 con proba 1 -p Jacques Bernoulli 1654 - 1705 Jacques Bernoulli (capítulo 5, Parte IV del Ars conjectandi ). 14

TEOREMA DEL LIMITE CENTRAL: ERRORES Xn independientes Xn =1 con proba p Xn = 0 con proba 1 -p Pierre-Simon Laplace 1749 -1827 Johann Carl Friedrich Gauss 1777 - 1855 15

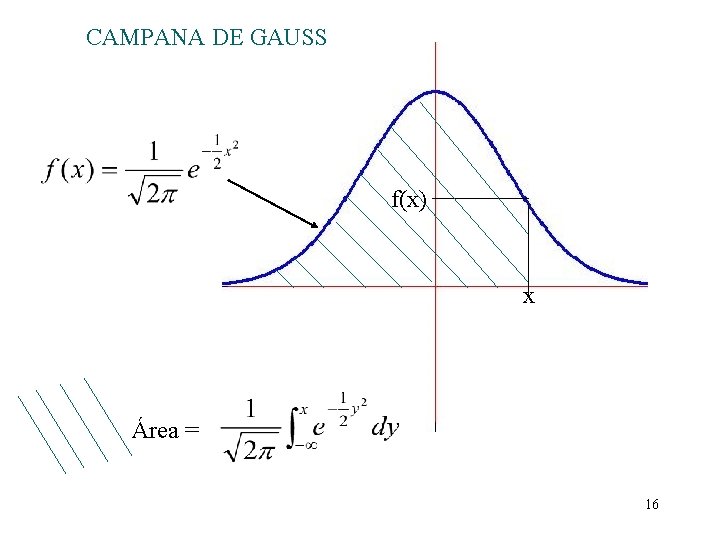
CAMPANA DE GAUSS f(x) x Área = 16

NACIMIENTO DE LA TEORIA DE PROBABILIDADES Hay dos jugadores. El total de lo apostado es ganado por el jugador que gana por primera vez N juegos. Supongamos que el primer jugador ha ganado k juegos y el segundo j juegos y se interrumpe la partida: ¿Cómo debe dividirse el total entre ambos jugadores? Blaise Pascal 1623 - 1662 17

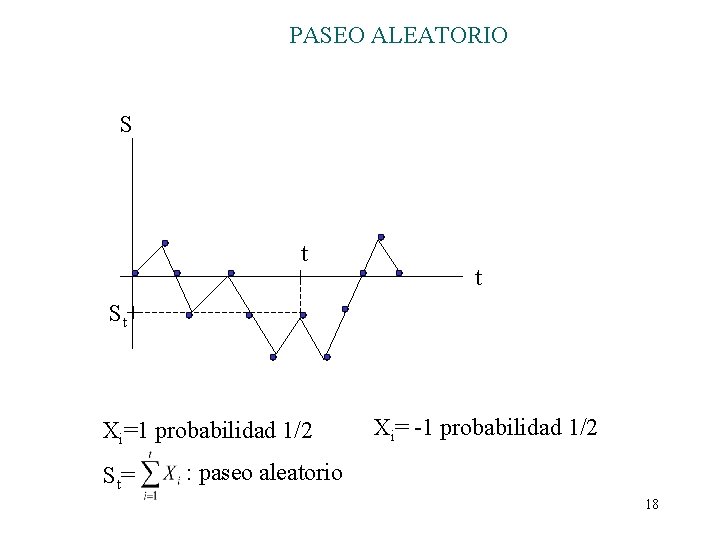
PASEO ALEATORIO S t t St + Xi=1 probabilidad 1/2 St = Xi= -1 probabilidad 1/2 : paseo aleatorio 18

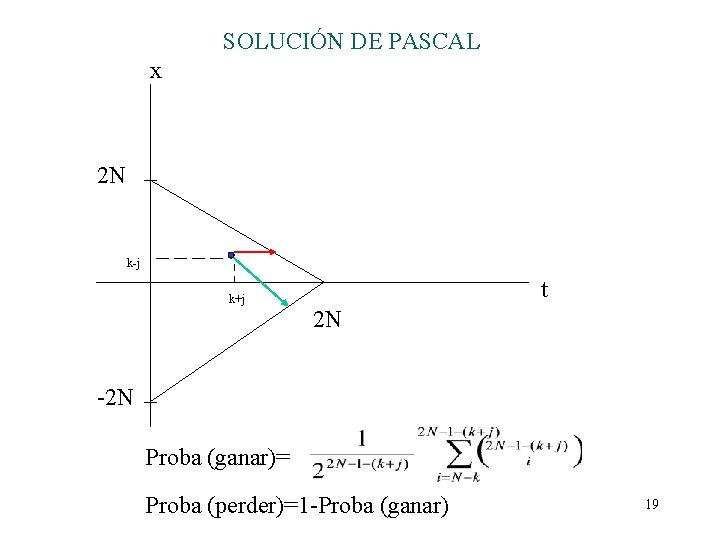
SOLUCIÓN DE PASCAL x 2 N k-j k+j t 2 N -2 N Proba (ganar)= Proba (perder)=1 -Proba (ganar) 19

MOVIMIENTO BROWNIANO (normalización del paseo aleatorio en tiempo y espacio) Norbert Wiener 1894 -1964 Trayectorias continuas 20

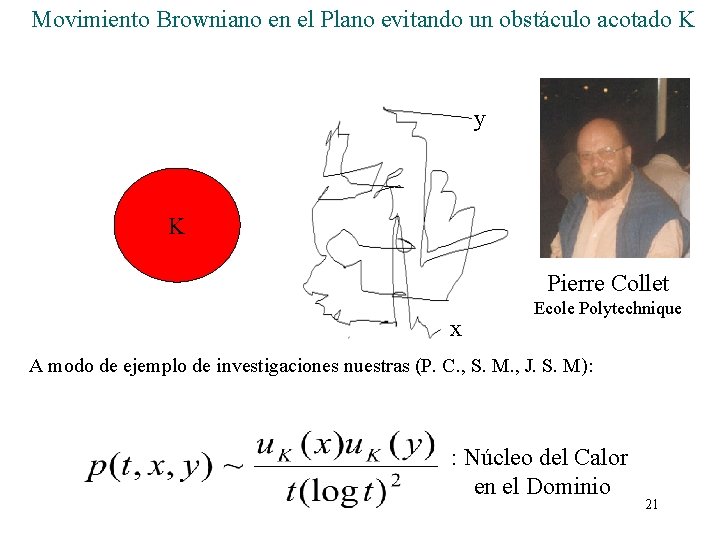
Movimiento Browniano en el Plano evitando un obstáculo acotado K y K Pierre Collet x Ecole Polytechnique A modo de ejemplo de investigaciones nuestras (P. C. , S. M. , J. S. M): : Núcleo del Calor en el Dominio 21

“ORIGEN DEL AZAR” Las probabilidades son la ciencia de la incertidumbre, cuyo origen se encuentra en: Equilibrio inestable (Dado) Sensibilidad a las condiciones iniciales (Dado, Ruleta) 22

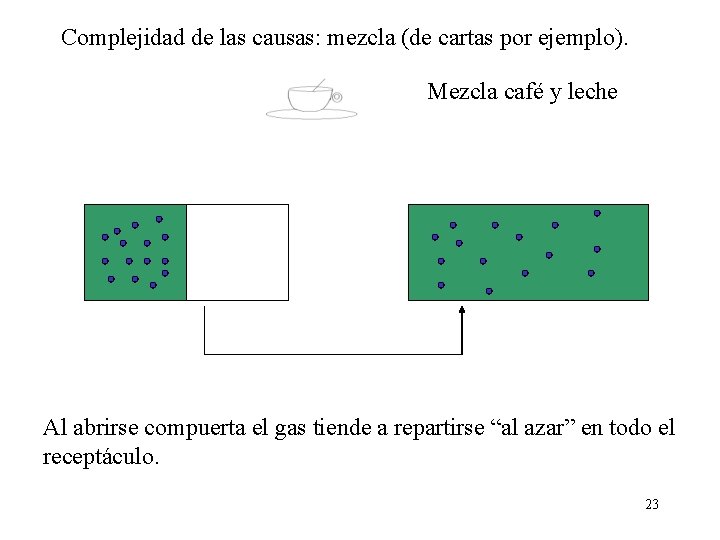
Complejidad de las causas: mezcla (de cartas por ejemplo). Mezcla café y leche Al abrirse compuerta el gas tiende a repartirse “al azar” en todo el receptáculo. 23

TEOREMA DE BOLTZMANN Densidad de moléculas velocidad v en tiempo t Debido a choques de moléculas entre sí es = 0 si f (v (t) ) es constante. Ludwig Boltzmann 1844 - 1906 Gracias a que las moléculas de gas chocan “aleatoriamente” se pueden formular leyes simples. Si éstas están “organizadas” las leyes son más difíciles de obtener. 24

Lema Recurrencia Poincaré: si medida A >0. HIPOTESIS ERGÓDICA Media Temporal Henri Poincaré 1854 -1912 Media Espacial Teorema de Von Neumann-Birkhoff: la hipotesis ergódica se verifica si no hay conjuntos invariantes. John von Neumann 1903 -1957 25

INFORMACIÓN Y ENTROPÍA Cinta Es 0 ó 1 Información depende de las unidades de bits. Si el mensaje es elegido de entre n mensajes equiprobables, la información será I(n). Si tengo dos mensajes independientes, uno elegido de entre n mensajes y otro de entre m mensajes, la información es I(n)+I(m). Si I(n) crece con n se deduce I(n)= log 2 n. Luego la información es el número de bits con que se escribe un mensaje (2 mensajes caben en 1 bit: 0 ó 1). Así I(2 n)=n. 26

Luego la entropía, que es la media de información de un experimento será log 2 n pues todos tienen igual información. En general si se elige un mensaje, siendo que el mensaje i tiene probabilidad pi, la información es log 1/ pi y la entropía es Es fácil ver que H(p) log 2 n, luego la entropía se maximiza si las probabilidades son iguales pi =1/n, i=1, . . . n. 27

Izquierda Empate Derecha 9 monedas: 8 son de peso igual, 1 de peso distinto. Determinar en una balanza cual es la moneda distinta y si es de peso mayor o menor que el resto. Hay 18 permutaciones, luego información Cada pesada da información promedio 2 pesadas , luego no se puede determinar. 3 pesadas y efectivamente se puede determinar cual es la moneda y si es más o menos pesada. *Gordon Raisbeck. Théorie de l’ Information, Masson, 1964. 28

SISTEMAS DE BERNOULLI (RULETAS) 1 1 F(x) 1 2 vueltas de ruleta 0 x 0 p 1 + p 2 1 Entropía: Ruleta generalizada Entropía (K-S): 29

ENTROPIA EN TEORIA ERGODICA Entropía es invariante de Sistemas dinámicos abstractos: corresponde a la información media asintótica dada por el sistema en una unidad de tiempo. Para sistemas de Bernoulli se verifica que la entropía es invariante completo: Andrey Nikolaevich Kolmogorov 1903 - 1987 (D. Ornstein) 30

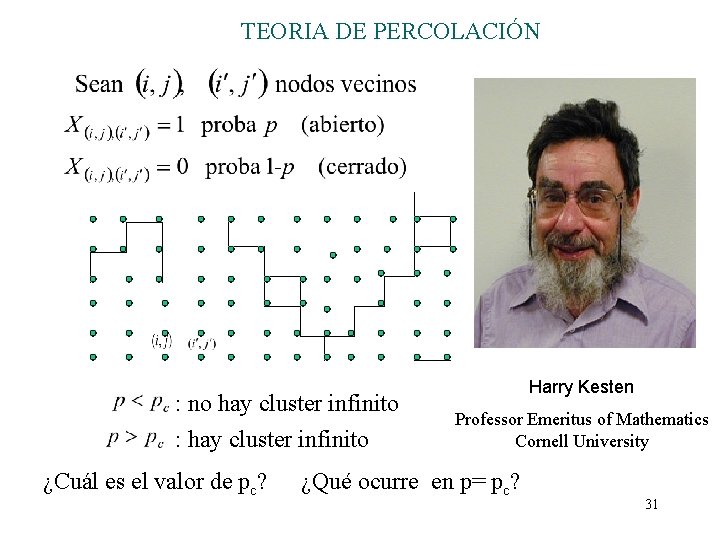
TEORIA DE PERCOLACIÓN : no hay cluster infinito : hay cluster infinito ¿Cuál es el valor de pc? Harry Kesten Professor Emeritus of Mathematics Cornell University ¿Qué ocurre en p= pc? 31

REDES DE TELECOMUNICACIONES (Loss Networks) R : Conjunto de rutas r : ruta determinada por enlaces que usa j 1 j 2 j 3 La ruta r usa Ajr circuitos del enlace j. Por ejemplo Cj: número total de circuitos del enlace j (capacidad). Si llega una llamada para usar la ruta r, ésta se efectúa si hay al menos Ajr circuitos disponibles del enlace j, si no la llamada se pierde. 32

Punto fijo de Erlang Si las llamadas que usan la ruta r llegan aleatoriamente a tasa (esto es según un proceso de Poisson). nr : número de llamadas que están usando la ruta r, el vector de llamadas de las diferentes rutas. Se verifica La distribución de equilibrio del sistema es: Probabilidad n ~ 33

GENOMICA (Laboratorio de Bioinformática y Matemáticas del Genoma) Zonas codificantes y zonas no-codificantes tiene distintas estructuras de memoria: 34

Distribución Granulométrica: Cantera Sesgo en Estimación por Efecto Frontera Las fotografías son analizadas con un marco, hay dos granulometrías estudiadas por J. B. y S. M. Una subestima y la otra subestima la granulometría real (análogo Paradoja 35 Tiempo de Espera).

NUMEROS NORMALES Casi todos los números son normales, esto es son variables independientes uniformes en los dígitos {0, 1, . . . , 9}: ¿ Es = 3. 14159. . . un número normal? PROBLEMA DEL CUMPLEAÑOS ¿Cuál es la probabilidad para que entre n personas, haya al menos de ellas que cumplan años el mismo día? Sean independientes uniformes en {1, 2, . . . , 365} Sea N el más pequeño tal que Se dispone Applet Problema de Coleccionista de Albúm. 36

PROBLEMAS QUE NO HEMOS TRATADO: Probabilidades en Ciencias Sociales: Probabilidades Subjetivas. Ejemplo: Apuestas en Carreras de Caballos. Por una cabeza De un noble potrillo Que justo en la raya Afloja al llegar. Y que al regresar Parece decir No olvides, hermano, Vos sabes no hay que jugar. Basta de carrera: Se acabo la timba, Un final reñido Carlos Gardel. 1890 - 1935 Yo no vuelvo a ver. Pero si algún pingo Llega a ser fija el domingo Yo me juego entero ¡ que le voy a hacer ¡ * Extracto de “Por una Cabeza” (Tango de C. Gardel y A. Lepera) 37
 Dominio y recorrido
Dominio y recorrido Funcion creciente en todo su dominio
Funcion creciente en todo su dominio Que es el movimiento
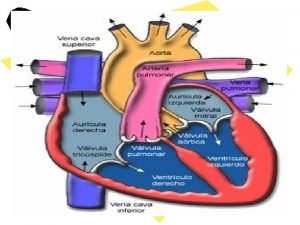
Que es el movimiento Aparato circulatorio
Aparato circulatorio Naricera fio2
Naricera fio2 Croquis de recorrido
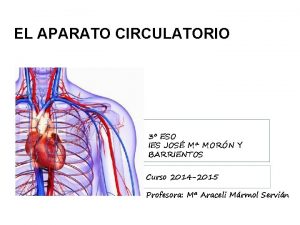
Croquis de recorrido Aparato circulatorio 3 eso
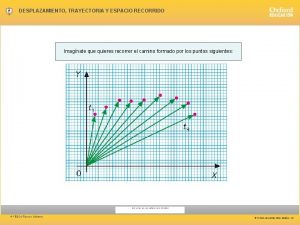
Aparato circulatorio 3 eso Diagrama de recorrido
Diagrama de recorrido Antonio ha recorrido la quinta parte de un camino recto
Antonio ha recorrido la quinta parte de un camino recto Eje hipotalamo hipofisis
Eje hipotalamo hipofisis Repermeabilizacion de la vena umbilical
Repermeabilizacion de la vena umbilical Danubio stati attraversati
Danubio stati attraversati Imagnate
Imagnate Terranova titanic
Terranova titanic Recorrido en una funcion
Recorrido en una funcion Vena axilar
Vena axilar Arteria renal origen
Arteria renal origen Rio volga recorrido
Rio volga recorrido Aceleración normal y aceleración tangencial
Aceleración normal y aceleración tangencial Arbol postorden
Arbol postorden Nanocrystal
Nanocrystal The things they carried controversy
The things they carried controversy Personaje al azar
Personaje al azar Que dice la biblia sobre los juegos
Que dice la biblia sobre los juegos Emprendedor rastreador
Emprendedor rastreador Al azar
Al azar Dr azar kardan
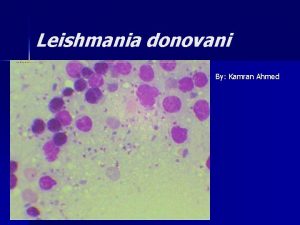
Dr azar kardan Etiologi leishmaniasis
Etiologi leishmaniasis Juegos de azar justos
Juegos de azar justos Azar interactive
Azar interactive Técnica del azar ejemplos
Técnica del azar ejemplos Historia de los juegos de azar
Historia de los juegos de azar Alice azar
Alice azar Que dice la biblia sobre los juegos de azar
Que dice la biblia sobre los juegos de azar Chagoma
Chagoma Que zica hein
Que zica hein Steven miles md
Steven miles md Vengo desde el ayer
Vengo desde el ayer