Eigenvalues and geometric representations of graphs Lszl Lovsz

Eigenvalues and geometric representations of graphs László Lovász Microsoft Research One Microsoft Way, Redmond, WA 98052 lovasz@microsoft. com

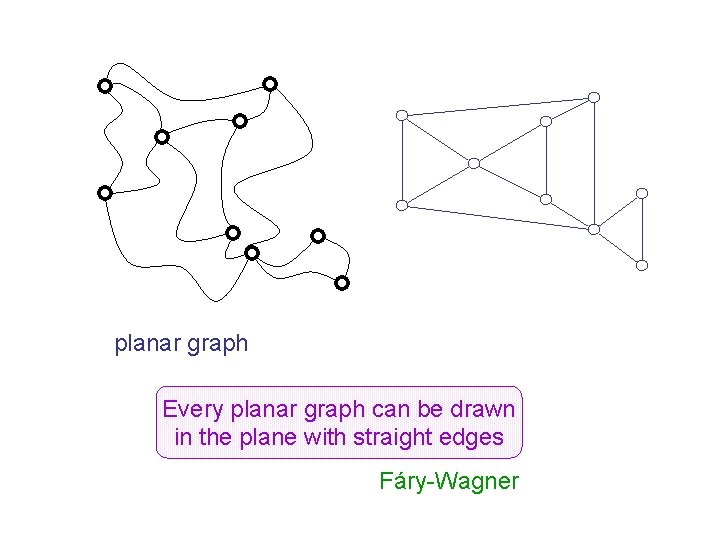
planar graph Every planar graph can be drawn in the plane with straight edges Fáry-Wagner

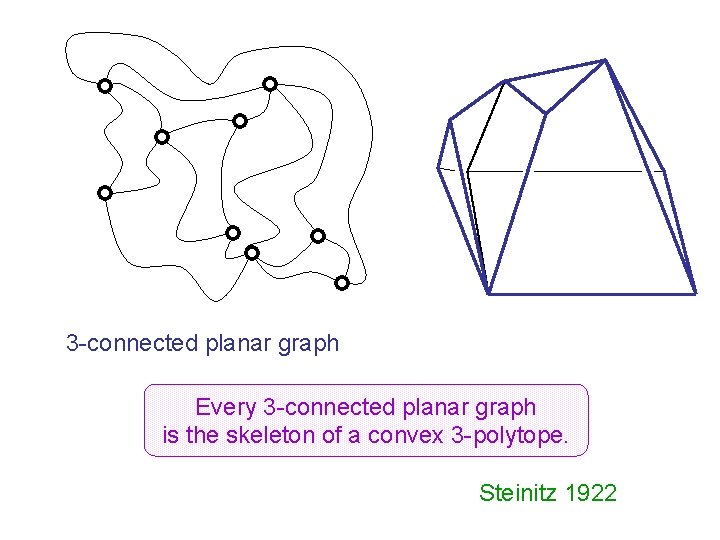
3 -connected planar graph Every 3 -connected planar graph is the skeleton of a convex 3 -polytope. Steinitz 1922

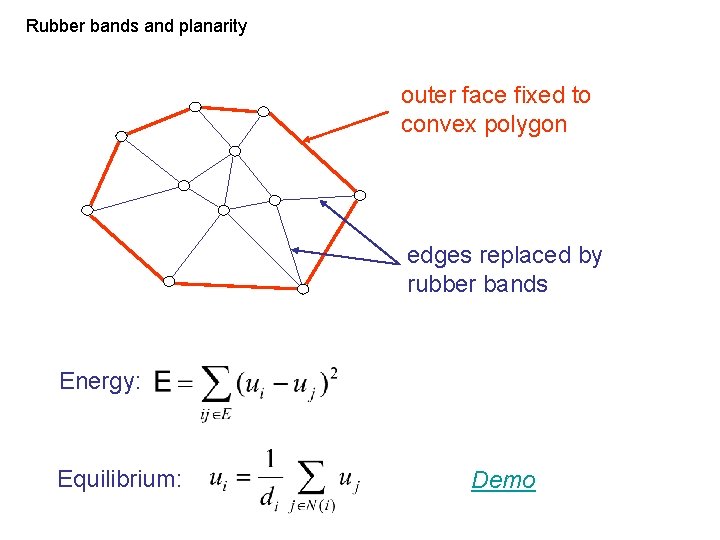
Rubber bands and planarity Every 3 -connected planar graph can be drawn with straight edges and convex faces. Tutte (1963)

Rubber bands and planarity outer face fixed to convex polygon edges replaced by rubber bands Energy: Equilibrium: Demo

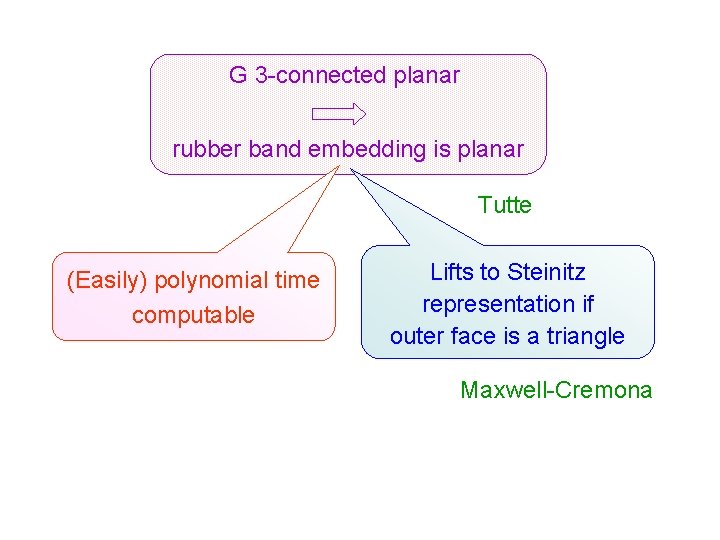
G 3 -connected planar rubber band embedding is planar Tutte (Easily) polynomial time computable Lifts to Steinitz representation if outer face is a triangle Maxwell-Cremona

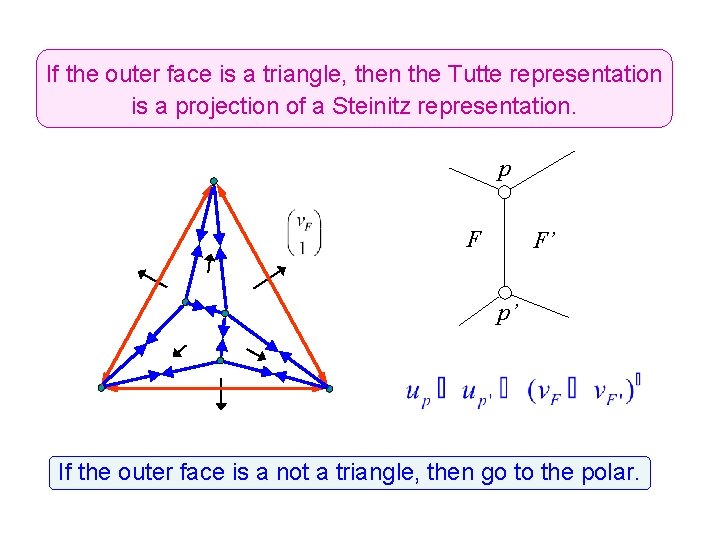
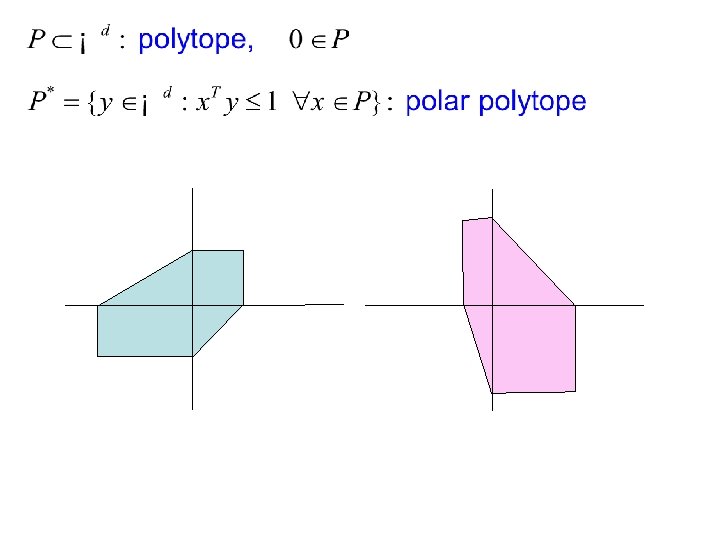
If the outer face is a triangle, then the Tutte representation is a projection of a Steinitz representation. p F F’ p’ If the outer face is a not a triangle, then go to the polar.

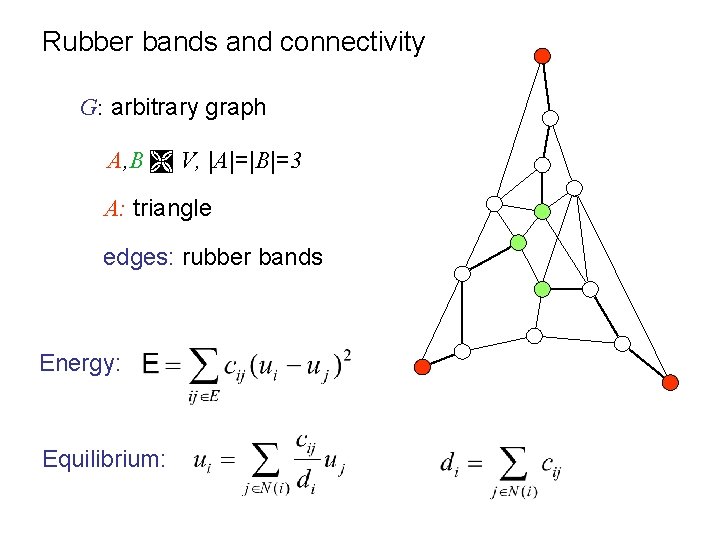
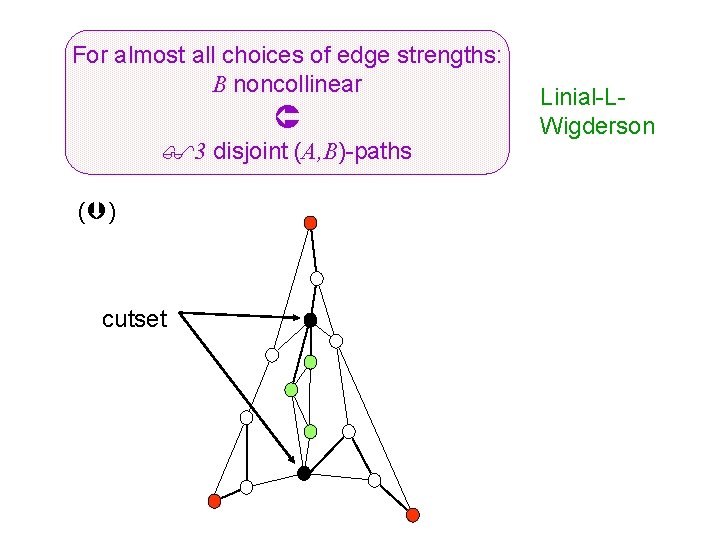
Rubber bands and connectivity G: arbitrary graph A, B V, |A|=|B|=3 A: triangle edges: rubber bands Energy: Equilibrium:

For almost all choices of edge strengths: B noncollinear 3 disjoint (A, B)-paths ( ) cutset Linial-LWigderson

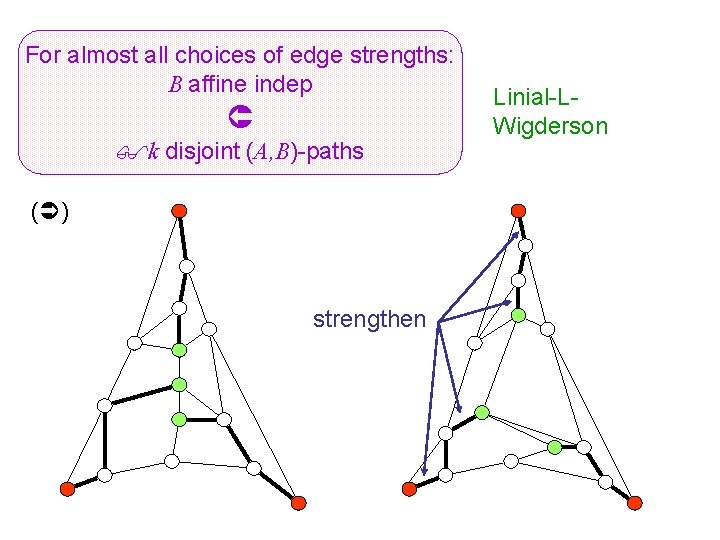
For almost all choices of edge strengths: B affine indep k disjoint (A, B)-paths ( ) strengthen Linial-LWigderson

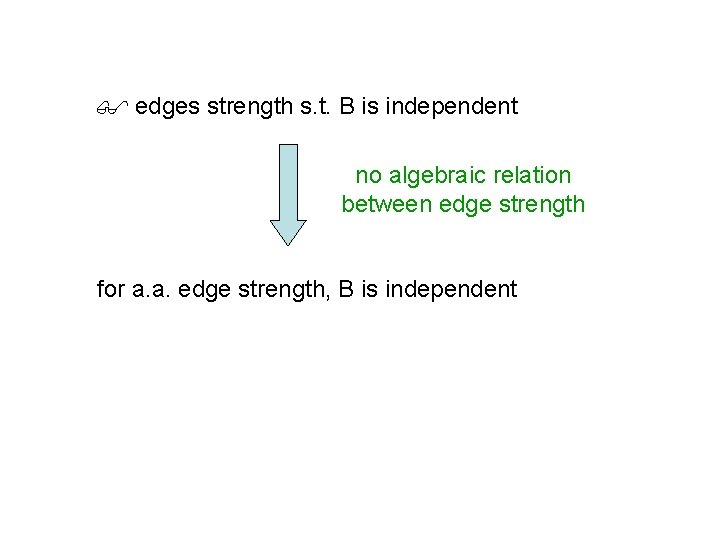
edges strength s. t. B is independent no algebraic relation between edge strength for a. a. edge strength, B is independent

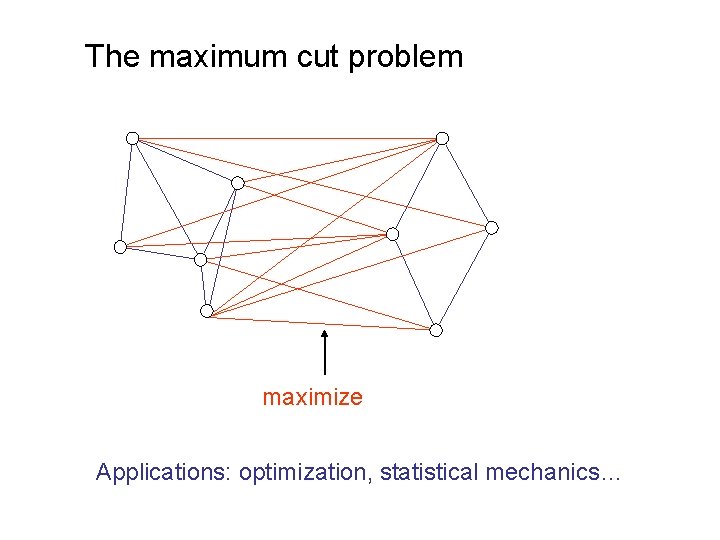
The maximum cut problem maximize Applications: optimization, statistical mechanics…

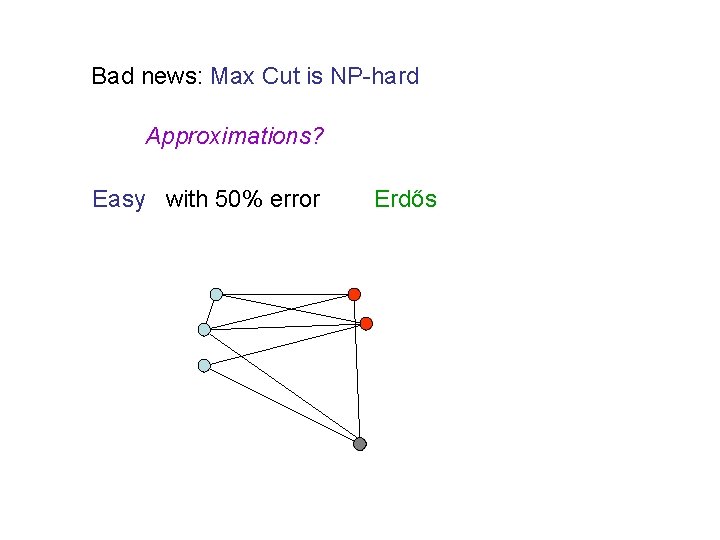
Bad news: Max Cut is NP-hard Approximations? Easy with 50% error C Erdős

Bad news: Max Cut is NP-hard Approximations? Easy with 50% error C Erdős

Bad news: Max Cut is NP-hard Approximations? Easy with 50% error Erdős

Bad news: Max Cut is NP-hard Approximations? Easy with 50% error Erdős

Bad news: Max Cut is NP-hard Approximations? Easy with 50% error Erdős

Bad news: Max Cut is NP-hard Approximations? Easy with 50% error Erdős

Bad news: Max Cut is NP-hard Approximations? Easy with 50% error Erdős

Bad news: Max Cut is NP-hard Approximations? Easy with 50% error Erdős NP-hard with 6% error Hastad Polynomial with 12% error Goemans-Williamson

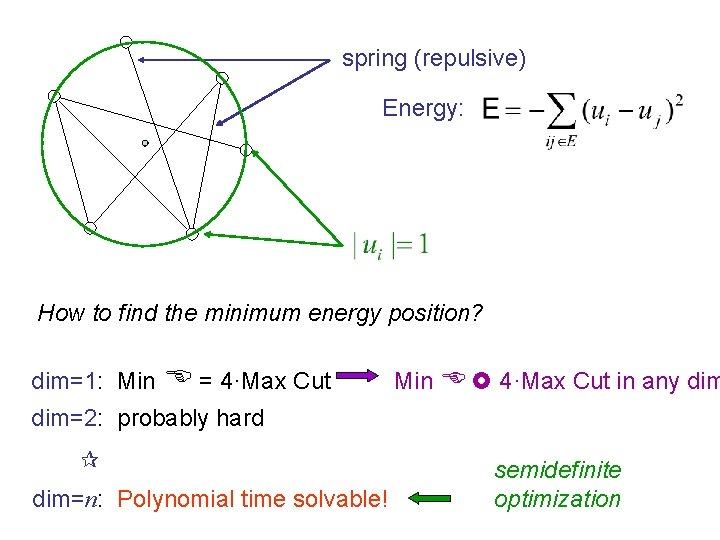
spring (repulsive) Energy: How to find the minimum energy position? dim=1: Min E = 4·Max Cut Min E 4·Max Cut in any dim=2: probably hard dim=n: Polynomial time solvable! semidefinite optimization

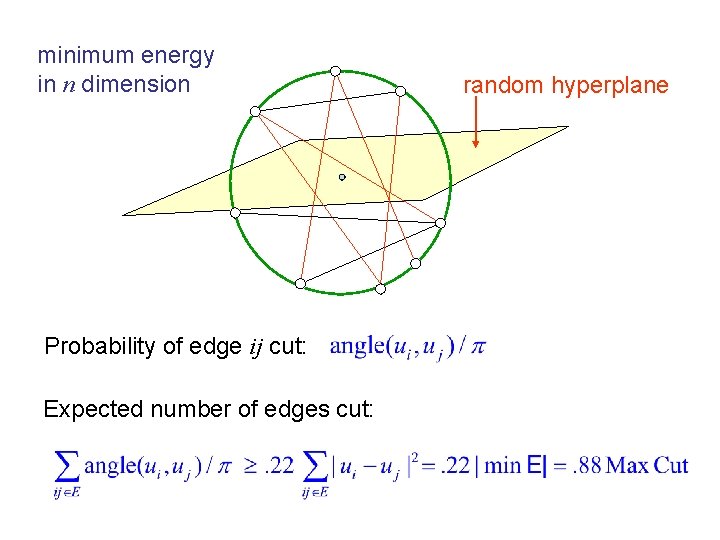
minimum energy in n dimension Probability of edge ij cut: Expected number of edges cut: random hyperplane

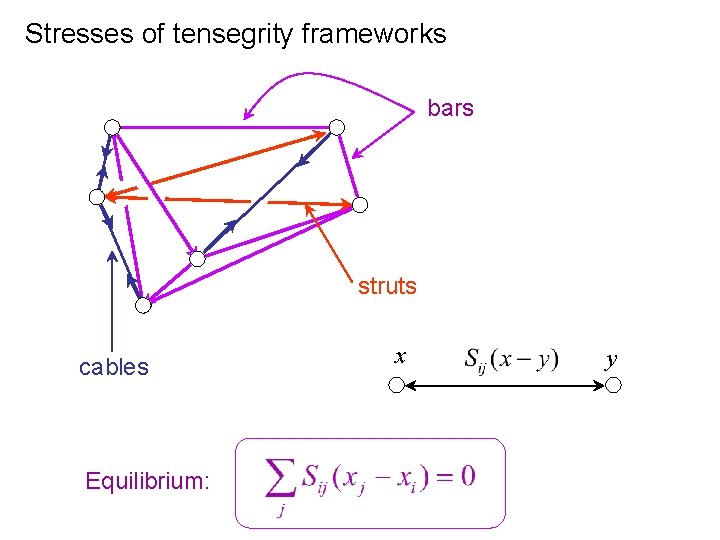
Stresses of tensegrity frameworks bars struts cables Equilibrium: x y

There is no non-zero stress on the edges of a convex polytope Cauchy Every simplicial 3 -polytope is rigid.

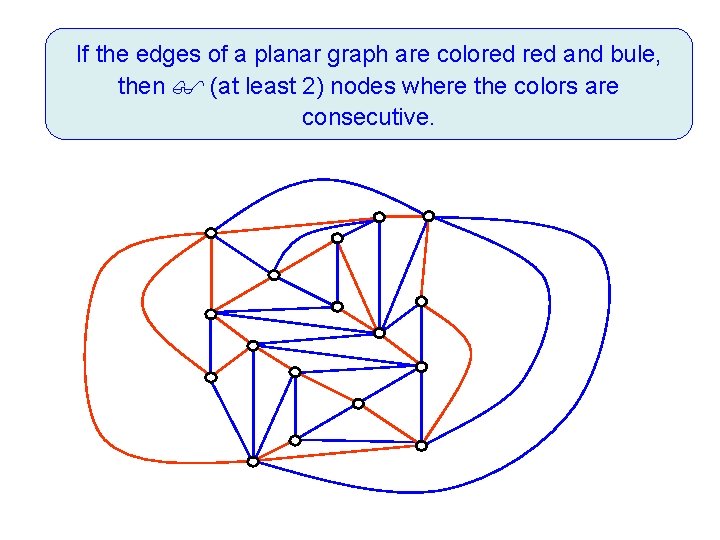
If the edges of a planar graph are colored and bule, then (at least 2) nodes where the colors are consecutive.

10 3 9 3 3 2 4 1 9 2 3 5 2 10

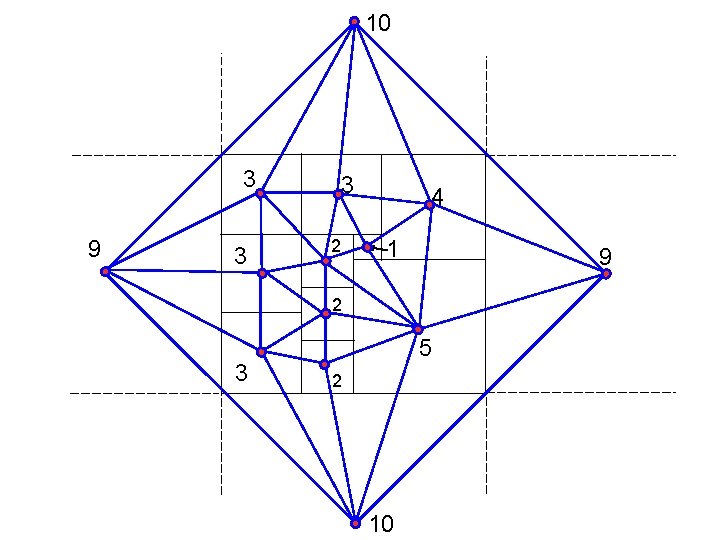
Every triangulation of a quadrilateral can be represented by a square tiling of a rectangle. Schramm

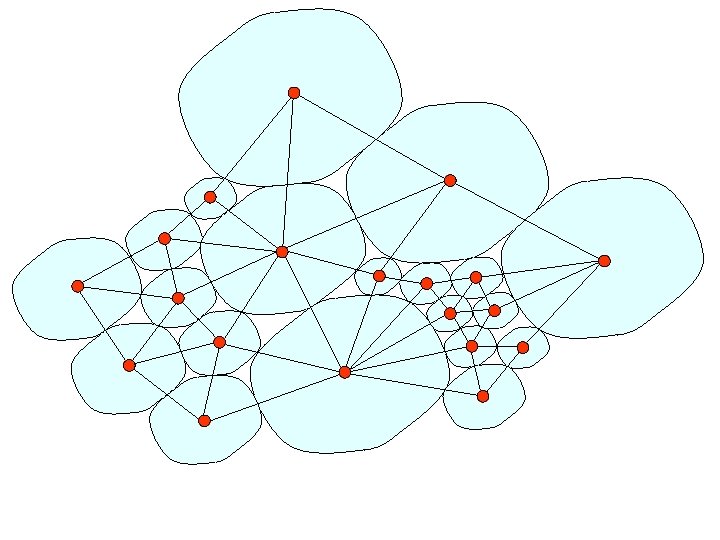
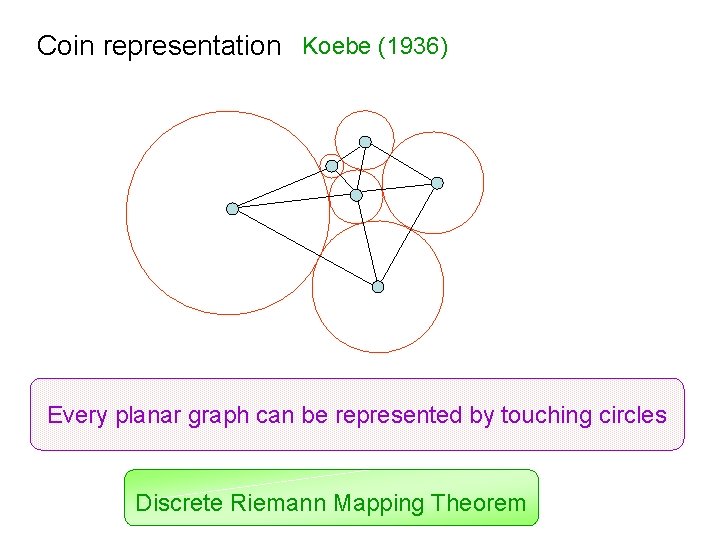
Coin representation Koebe (1936) Every planar graph can be represented by touching circles Discrete Riemann Mapping Theorem

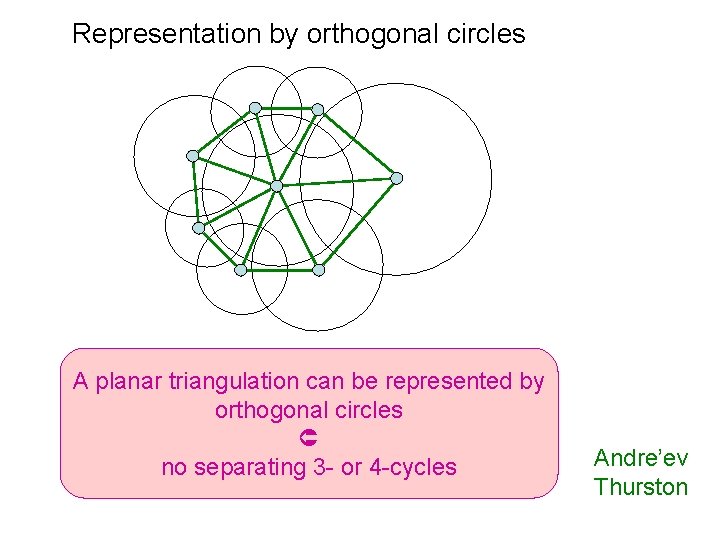
Representation by orthogonal circles A planar triangulation can be represented by orthogonal circles no separating 3 - or 4 -cycles Andre’ev Thurston

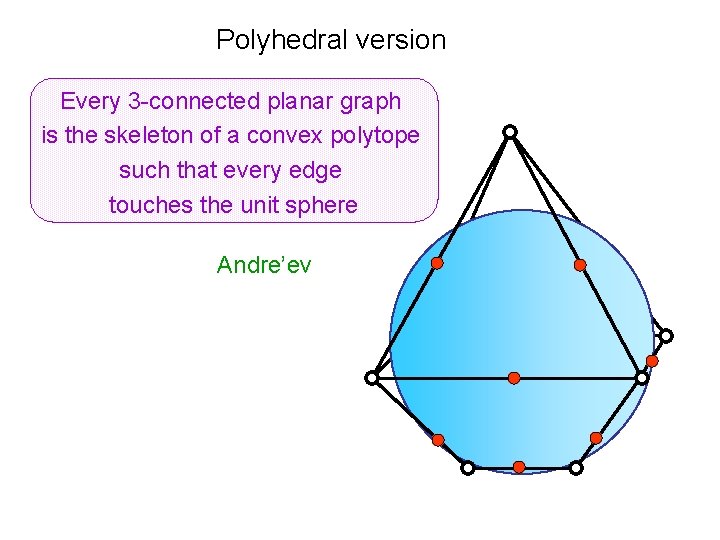
Polyhedral version Every 3 -connected planar graph is the skeleton of a convex polytope such that every edge touches the unit sphere Andre’ev

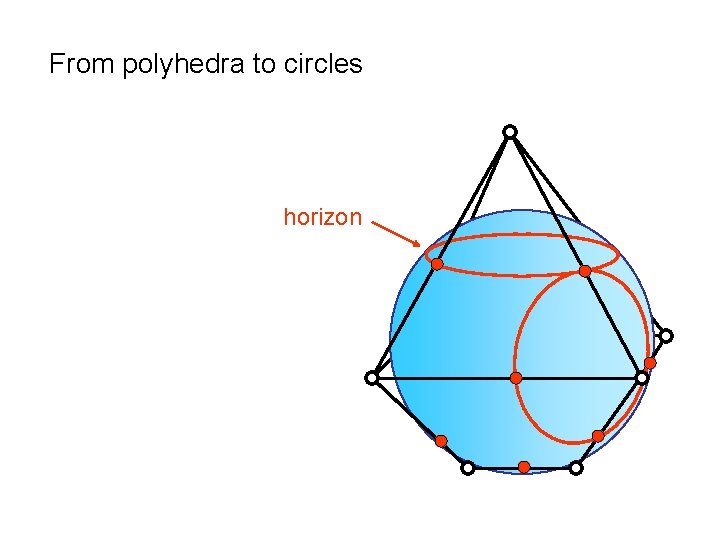
From polyhedra to circles horizon

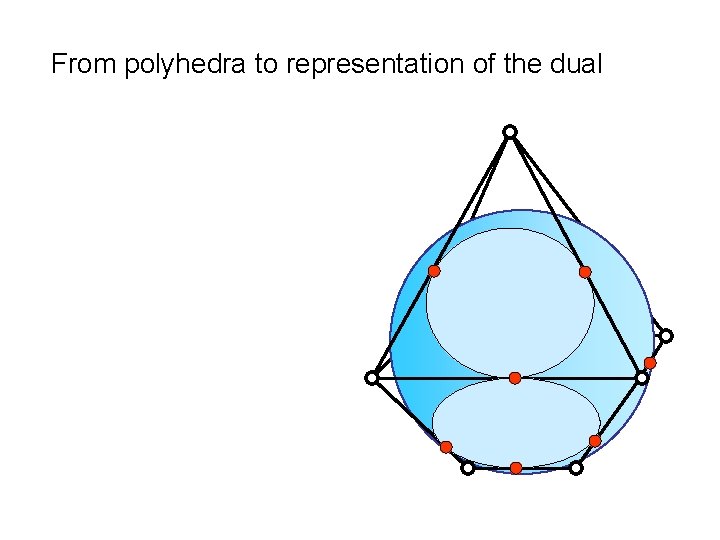
From polyhedra to representation of the dual