Effective Field Theory including vector mesons in addition

Effective (Field) Theory including vector mesons in addition to pseudoscalar mesons • M. Bando, T. Kugo and K. Yamawaki, Phys. Rept. 164, 217 (1988). • M. Harada and K. Yamawaki, Phys. Rept. 381, 1 (2003).

☆ Chiral Perturbation Theory EFT for π J. Gasser and H. Leutwyler, Annals Phys. 158, 142 (1984); NPB 250, 517 (1985) P-wave ππ scattering 1 -loop tree

☆ What EFT do we need to include r and p ? ◎ several ways to include r • Matter field • Anti-symmetric tensor field • Massive Yang-Mills • Hidden local symmetry These are all equivalent at tree level. A difference appears at loop level. ◎ Hidden Local Symmetry Theory ・・・ EFT for r and p M. Bando, T. Kugo, S. Uehara, K. Yamawaki and T. Yanagida, PRL 54 1215 (1985) M. Bando, T. Kugo and K. Yamawaki, Phys. Rept. 164, 217 (1988) M. H. and K. Yamawaki, Physics Reports 381, 1 (2003 based on chiral symmetry of QCD ρ ・・・ gauge boson of the HLS

☆ Chiral Lagrangian Non-Linear Realization of Chiral Symmetry SU(Nf )L×SU(N )f R→ SU(N )f V ◎ Basic Quantity U=e 2 iπ a. T a/F π → g. L U g †R ; g. L, R∈ SU(N f) L, R ◎ Lagrangian L 2 Fπ μ = tr［∇μU ∇ U 4 † ］ ∇μ U ≡∂ Uμ － i L Uμ + i U R L μ, R μ; gauge fields of SU(N )f μ L, R

☆ Hidden Local Symmetry M. Bando, T. Kugo, S. Uehara, K. Yamawaki and T. Yanagida, PRL 54, 1215 (1985) M. Bando, T. Kugo and K. Yamawaki, Phys. Rept. 164, 297 (1988) U=e 2 iπ/ F π =ξ † L ξ R Fπ , Fσ ・・・ Decay constants of π and σ h ∈ ［SU(N f ) V ］local g L, R ∈ ［SU(N f ) L, R ］global ・ Particles ρ μ= ρ Tμa ・・・ HLS gauge boson a π=π a. T a・・・ NG boson of ［SU(N )f × ］ L SU(N ) f R symmetry breaking a σ=σ T ・・・ NG boson of ［SU(N )f ］V a symmetry breaking local global

• Maurer-Cartan 1 -forms 変換性 ： • Lagrangian

4. 3 Phenomenology at tree level

☆ Low Energy Theorem Exact in the low energy limit ; pρ2 = 0 gauge boson --- well-defined off-shell ☆ KSRF I (on-shell ; pρ２ = mρ２ ) ? ?

☆ KSRF I (on-shell ; pρ２ = mρ２) ? ? 15% deviation !!

☆ Values of Parameters

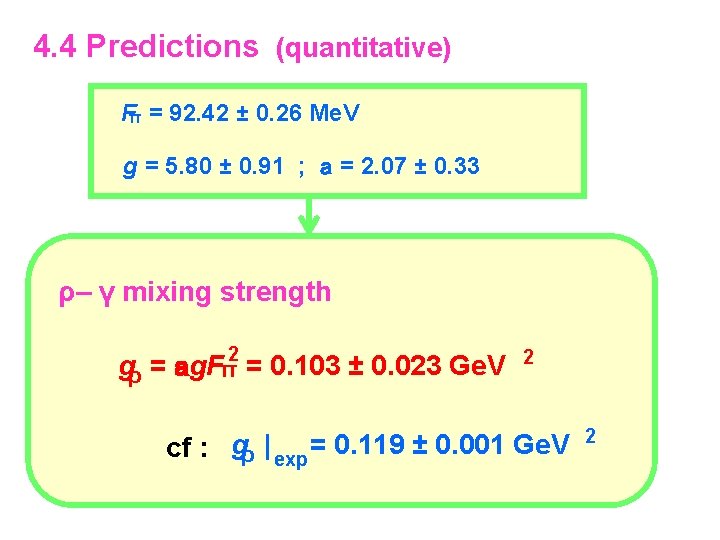
4. 4 Predictions (quantitative) Fπ = 92. 42 ± 0. 26 Me. V g = 5. 80 ± 0. 91 ; a = 2. 07 ± 0. 33 ρ– γ mixing strength 2 gρ = ag. Fπ = 0. 103 ± 0. 023 Ge. V 2 cf : gρ | exp = 0. 119 ± 0. 001 Ge. V 2

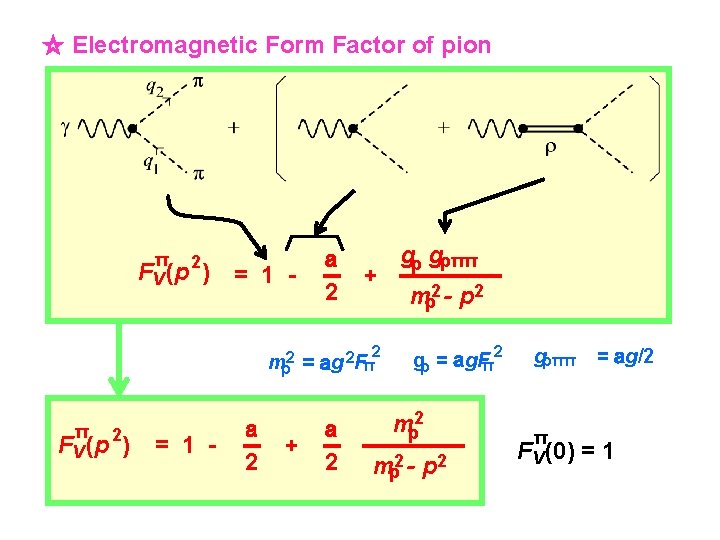
☆ Electromagnetic Form Factor of pion π FV (p 2) = 1 - a 2 + 2 mρ2 = ag 2 Fπ π 2 FV (p ) = 1 - a 2 + gρ gρππ mρ2 - p 2 gρ = ag. Fπ2 a mρ2 2 mρ2 - p 2 gρππ π = ag/2 FV (0) = 1

☆ charge radius of pion π 2 FV (p ) = 1 - a 2 + a mρ2 2 mρ2 - p 2 3 a = 1 + 6 mρ2 〈r 〈r 2 π 〉V = 2 π 〉V | exp 3 a mρ2 + ・・・ = 0. 407 ± 0. 064 (fm) 2 = 0. 452 ± 0. 011 ; (PDG 2006)

☆ Integrating out vector mesons in the low energy region at tree level EOM for Vμ (Vμ = gρμ) 1 ν 2 a. Fπ (Vμ – α //μ) - 2(∂ V μν– i [ V , ν V μν] ) = 0 g 1 Vμ = α //μ+ O(p 3) ; α //μ= (D μξ ・ξR +†RD ξ ・ξμ )L/(2 i†L) mρ2 Dμξ R= ∂ ξμ－ Ri R ξ μ identity α＾⊥μ= 1 i † ξ・∇ U・ξ = R ξ 2 i・∇U μ R ・ξ μ L 2 † † L Chiral Lagrangian with O(p 4 ) terms ; U=ξ † ・ξ L R R

g = 5. 80 ± 0. 91 G. Ecker, J. Gasser, A. Pich and E. de. Rafael, NPB 321, 311 (1989)

☆ Correspondence between parts of MFM and those of HLS ▽ HLS in the unitary gauge ・・・ σ＝ 0 † ξ R ＝ξ ＝ξ L ; (C) ρ μ ＝ζ(α － ＝ζα //μ V ) μ ＾ //μ All the building blocks of the MFM are expressed by those of the HLS. For any Lagrangian of the MFM, whatever the form it takes, we can construct the equivalent Lagrangian of the HLS.

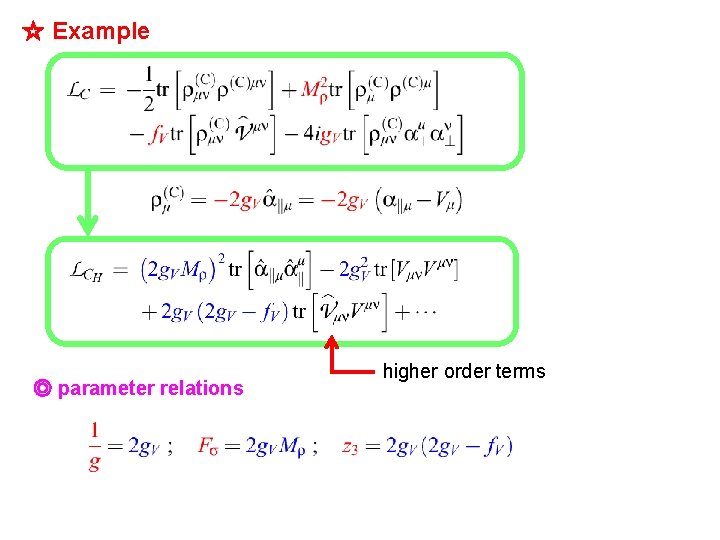
☆ Example ◎ parameter relations higher order terms

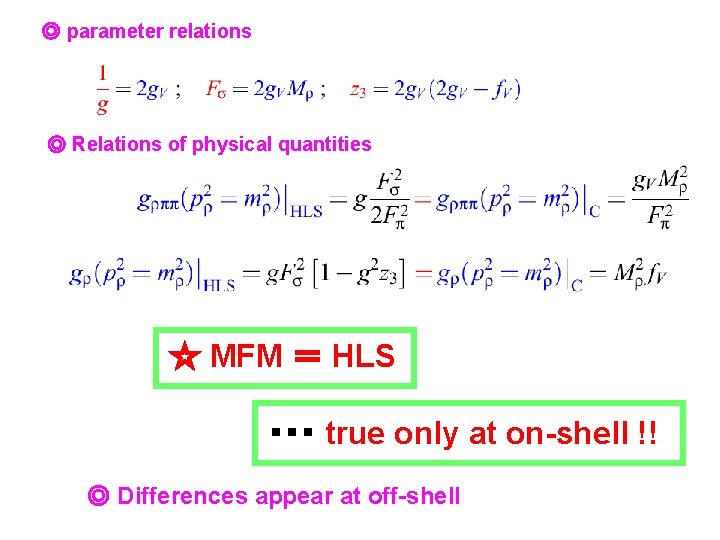
◎ parameter relations ◎ Relations of physical quantities ☆ MFM ＝ HLS ・・・ true only at on-shell !! ◎ Differences appear at off-shell

◎ In-equivalence for off-shell ρ

☆ Generalization of Wess-Zumino action ・・・ inclusion of vector mesons based on the HLS ◎ Wess-Zumino anomaly equation ◎ general solution

☆ VVπ, Vγπ, γγπ vertices

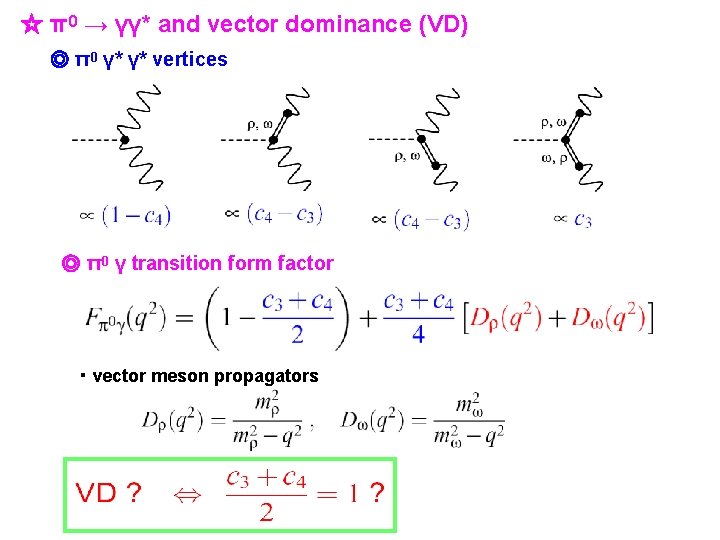
☆ π0 → γγ* and vector dominance (VD) ◎ π0 γ* γ* vertices ◎ π0 γ transition form factor ・ vector meson propagators

◎ determination of (c 3+c 4)/2 from experiment