ECUACIONES DE PRIMER Y DE SEGUNDO GRADO Definicin

ECUACIONES DE PRIMER Y DE SEGUNDO GRADO Definición. Algoritmo de resolución. 3 4 SÓLO CON UN TÉRMINO CON LA INCÓGNITA. 5 CON MÁS DE UN TÉRMINO CON LA INCÓGNITA. 6 ECUACIONES CON PARENTESIS QUE CONTIENEN TÉRMINOS CON LA INCÓGNITA (APLICANDO LA PROPIEDAD DISTRIBUTIVA DEL PRODUCTO RESPECTO A LA SUMA O 10 RESTA). Y ADEMÁS CON DENOMINADORES. ¿Hacemos algún problema utilizando ecuaciones de primer grado?

Tipos de problemas: Aritméticos. Geométricos. De mezclas. De edades. De móviles. De grifos

Definición: Podríamos decir que una ecuación de primer grado con una sola incógnita, es una igualdad que contiene una letra que llamamos incógnita. Se llama incógnita ya que su valor es desconocido y precisamente nuestra objetivo va a ser descubrir el valor que debe tomar para satisfacer la igualdad propuesta. Es decir, Lo que llamamos ecuación. Quizá valga la pena destacar que el tratamiento que se le da a la ecuación no puede ser diferente al permitido en una igualdad numérica. 3

ALGORITMO DE RESOLUCIÓN Todo se basa en que las operaciones hechas a ambos lados de las igualdades deben ser las Mismas, porque lo que estamos haciendo es transformar nuestras igualdades en otras equivalentes Por ejemplo: 24=24 es una igualdad numérica SI EN ELLA SUMAMOS, RESTAMOS, MULTIPLICAMOS O DIVIDIMOS POR UN MISMO NÚMERO OBTENEMOS IGUALDADES A PARTIR DE LA PREIMERA CON TODA SEGURIDAD. SUMAR: 24+12=24+12 RESTAR: 24 -8=24 -8 36=36 16=16 MULTIPLICAR: 24 X 5=24 X 5 120=120 DIVIDIR: 24: 4=24: 4 6=6 4

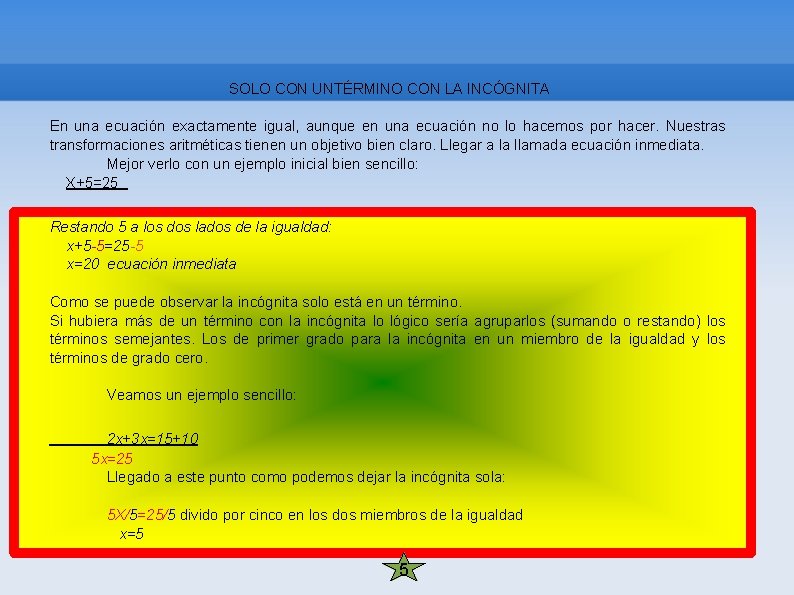
SOLO CON UNTÉRMINO CON LA INCÓGNITA En una ecuación exactamente igual, aunque en una ecuación no lo hacemos por hacer. Nuestras transformaciones aritméticas tienen un objetivo bien claro. Llegar a la llamada ecuación inmediata. Mejor verlo con un ejemplo inicial bien sencillo: X+5=25 Restando 5 a los dos lados de la igualdad: x+5 -5=25 -5 x=20 ecuación inmediata Como se puede observar la incógnita solo está en un término. Si hubiera más de un término con la incógnita lo lógico sería agruparlos (sumando o restando) los términos semejantes. Los de primer grado para la incógnita en un miembro de la igualdad y los términos de grado cero. Veamos un ejemplo sencillo: 2 x+3 x=15+10 5 x=25 Llegado a este punto como podemos dejar la incógnita sola: 5 X/5=25/5 divido por cinco en los dos miembros de la igualdad x=5 5

CON MÁS DE UN TÉRMINO CON LA INCÓGNITA Sin embargo, no siempre los términos semejantes están en el mismo miembro de la igualdad. Por lo que nuestra transformación aritmética irá dirigida a agrupar los términos semejantes en el mismo miembro de la igualdad, sumando o restando aquello que es necesario para que esto suceda. Lo mejor será verlo con un ejemplo: 5 x+15=2 x+30 Para agrupar los términos de primer grado en el primer miembro de la igualdad tendríamos que restar 2 x en los dos miembros de la igualdad. 5 x-2 x+15=2 x-2 x+30 Ya lo hemos conseguido. Ahora tendríamos que agrupar los términos de grado cero o coeficientes a la derecha de la igualdad. 3 x+15 -15=30 -15 Lo cual nos deja la siguiente situación: 3 x=15 Solo queda despejar la incógnita, o dejarla sola tal y como está permitido aritméticamente. Es decir dividir en el primer miembro de la igualdad y en el segundo por tres. 3 x/3=15/3 Llegando a la ecuación inmediata x=5 5

Lo único que restaría para poder asegurar que este valor también es solución de nuestra primera ecuación sólo faltaría sustituirlo en la ecuación inicial: 5 x+15=2 x+30 Es decir: 5*5+15=2*5+30 40=40 Vamos a adelantar un poco más. Nuestras ecuaciones pueden tener un aspecto un poco más complicado, porque aparte de tener varios términos con la incógnita “x”, puede que estén afectados por alguna operación e incluso afectados por algún nivel de jerarquía. Es, por tanto, importante hacer memoria de lo aprendido en la aritmética en lo referente a jerarquía y orden de operaciones.

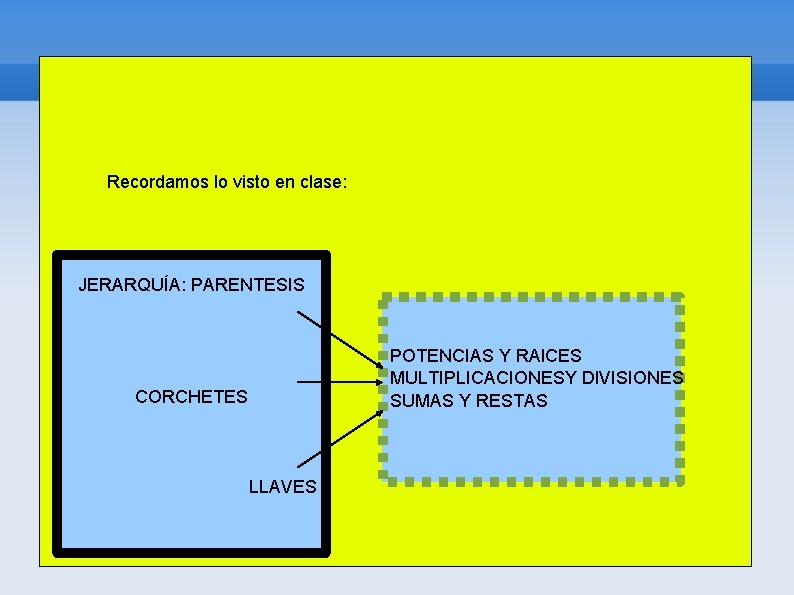
Recordamos lo visto en clase: JERARQUÍA: PARENTESIS POTENCIAS Y RAICES MULTIPLICACIONESY DIVISIONES SUMAS Y RESTAS CORCHETES LLAVES

UNA OPERACIÓN COMO ESTA: 2 X(32+5 X 23) 1ºDe las operaciones del paréntesis, las potencias: 2 x(9+5 x 8) 2ºDe las operaciones del paréntesis, productos: 2 X(9+40) 3ºDe las operaciones del paréntesis, las sumas: 2 X 49 4ºDe las operaciones quedan, ya sólo queda la suma: 98

ECUACIONES CON PARENTESIS QUE CONTIENEN TÉRMINOS CON LA INCÓGNITAS Teniendo en cuenta la jerarquía y orden de operaciones un a ecuación como esta: 2*(4 x-3)+3*(2 x+6)=5*(3 x+2) Dentro de cada uno de los parentesis no podemos hacer ni las multiplicaciones ni las sumas porqué una letra multiplicada por un número es como soplar contra corriente (no tiene sentido), así como sumar un número a una letra (tampoco no tiene sentido). Que opción nos queda. Vamos a utilizar la propiedad distributiva del producto respecto de la suma 2*4 x-2*3+3*2 x+3*6=5*3 X+5*2 8 X-6+6 X+18=15 X+10 Ya hemos conseguido deshacernos de los paréntesis. Lo queda es como antes ecuaciones con varios términos con la incógnita: 8 x+6 x-15 x=10+6 -18 -x=-2 X=2 10