ECUACIONES DE LA RECTA VECTORIAL ECUACIONES PARAMTRICAS Xx

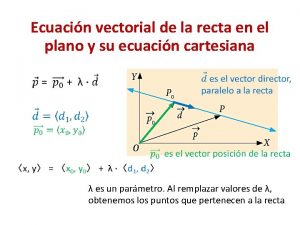
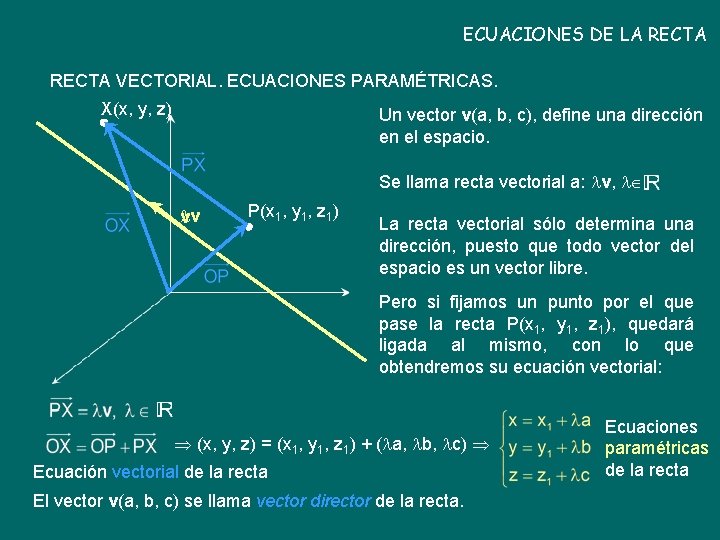
ECUACIONES DE LA RECTA VECTORIAL. ECUACIONES PARAMÉTRICAS. X(x, y, z) Un vector v(a, b, c), define una dirección en el espacio. Se llama recta vectorial a: v, v v P(x 1, y 1, z 1) La recta vectorial sólo determina una dirección, puesto que todo vector del espacio es un vector libre. Pero si fijamos un punto por el que pase la recta P(x 1, y 1, z 1), quedará ligada al mismo, con lo que obtendremos su ecuación vectorial: (x, y, z) = (x 1, y 1, z 1) + ( a, b, c) Ecuación vectorial de la recta El vector v(a, b, c) se llama vector director de la recta. Ecuaciones paramétricas de la recta

ECUACIONES DE LA RECTA Ejemplo: Halla las ecuaciones paramétricas de la recta que pasa por el punto P(1, 2, 3) y tiene la dirección del vector v(4, 5, 6) Punto P(1, 1 22, 33) Vector v(4, 4 5, 5 66) Ecuaciones paramétricas Debe tenerse en cuenta que tan importante como saber obtener las ecuaciones de una recta, es saber extraer información de las mismas. Así, si nos dicen que la recta r tiene ecuaciones paramétricas: , entonces, habremos de saber que un punto de la recta es el punto P(3, 1, 0), y que la dirección de la recta es la misma que la del vector v( 1, 0, 2)

ECUACIONES DE LA RECTA ECUACIONES EN FORMA CONTINUA. Partimos de las ecuaciones paramétricas: Despejamos el parámetro en las tres igualdades: = Ejemplo: Halla las ecuaciones en forma continua de la recta que pasa por el punto P(1, 0, 1) y tiene la dirección del vector v(2, 1, 1) Punto P(1, 1 0 0, ( 1) 1) Vector v(2, 2 1, 1 1 1) Ecuaciones en forma continua: No olvidemos el proceso inverso. Si las ecuaciones de una recta son: entonces, un punto de la recta es P( 1, 1, 0), su dirección es la del vector v(3, 2, 1)

ECUACIONES DE LA RECTA ECUACIONES EN FORMA IMPLÍCITA. Partimos de las ecuaciones en forma continua: b(x – x 1) = a(y – y 1) b(x – x 1) a(y – y 1) = 0 bx – ay + h = 0 c(x – x 1) = a(z – z 1) c(x – x 1) a(z – z 1) = 0 cx – az + k = 0 En general, las ecuaciones en forma implícita serán: Ejemplo: Halla las ecuaciones en forma implícita de la recta que pasa por el punto P(1, 0, 1) y tiene la dirección del vector v(2, 1, 1) En un apartado anterior, hemos obtenido las ecuaciones en forma continua: x + 2 y – 1 = 0 x 2 z – 3 = 0

ECUACIONES DE LA RECTA Ejemplo: Halla la ecuación de la recta que pasa por los puntos A(1, 2, 3) y B(6, 5, 4) A partir de estos dos puntos, podemos obtener las coordenadas de un vector director de la recta: v(6 – 1, 5 – 2, 4 – 3) v(5, 3, 1) Ecuaciones paramétricas: Ecuaciones en forma continua: Obsérvese que si A(x 1, y 1, z 1) y B(x 2, y 2, z 2) son dos puntos de la recta, las ecuaciones en forma continua vienen dadas por: Ecuaciones en forma implícita:

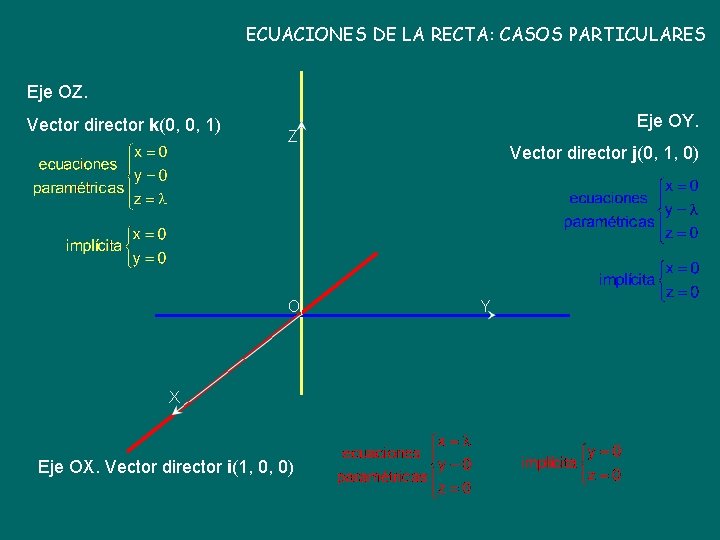
ECUACIONES DE LA RECTA: CASOS PARTICULARES Eje OZ. Vector director k(0, 0, 1) Eje OY. Z O X Eje OX. Vector director i(1, 0, 0) Vector director j(0, 1, 0) Y

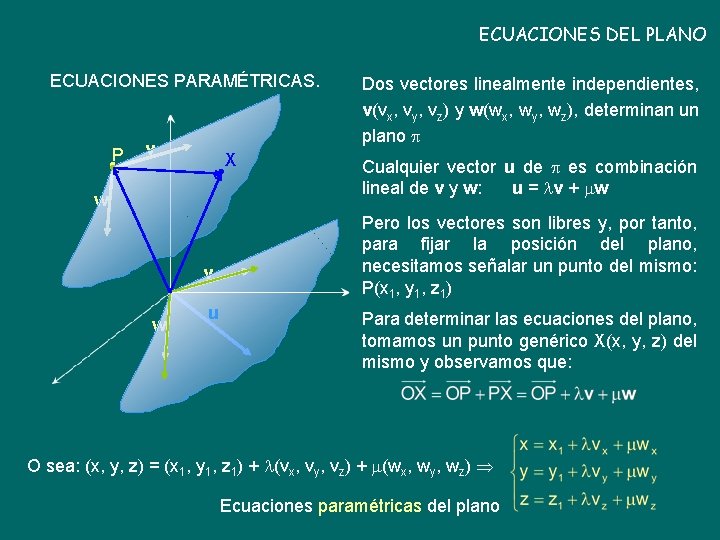
ECUACIONES DEL PLANO ECUACIONES PARAMÉTRICAS. P v X w v w u Dos vectores linealmente independientes, v(vx, vy, vz) y w(wx, wy, wz), determinan un plano Cualquier vector u de es combinación lineal de v y w: u = v + w Pero los vectores son libres y, por tanto, para fijar la posición del plano, necesitamos señalar un punto del mismo: P(x 1, y 1, z 1) Para determinar las ecuaciones del plano, tomamos un punto genérico X(x, y, z) del mismo y observamos que: O sea: (x, y, z) = (x 1, y 1, z 1) + (vx, vy, vz) + (wx, wy, wz) Ecuaciones paramétricas del plano

ECUACIONES DEL PLANO Ejemplo. Halla la ecuación del plano que contiene el punto P(1, 0, 2) y los vectores u(3, 2, 1) y v(2, 1, 3). Punto (1, 1 0 0, 22) Vectores: u(3, 3· 2, 2· 1· 1) v(2, 2· 1, 1· 3· 3) Ecuaciones paramétricas Debe tenerse en cuenta que tan importante como saber obtener las ecuaciones de un plano, es saber extraer información de las mismas. Así, si nos dicen que el plano tiene ecuaciones paramétricas: , entonces, habremos de saber que un punto del plano es el punto P(3, 1, 0), y que en el plano hay dos direcciones linealmente independientes determinadas por los vectores v( 1, 0, 2) y w(2, 3, 0)

ECUACIONES DEL PLANO ECUACIÓN IMPLÍCITA O GENERAL Dadas las ecuaciones paraméticas: eliminamos los parámetros y . Para ello, consideramos dichos parámetros como incógnitas y aplicamos las condiciones de compatibilidad del teorema de Rouché, es decir, la matriz ampliada ha de tener rango 2: Esta expresión nos da también un procedimiento para encontrar la ecuación general del plano, que, una vez desarrollado el determinante, tomará la forma: Ax + By + Cz + D = 0

ECUACIONES DEL PLANO Ejemplo: Halla la ecuación del plano determinado por los puntos A(1, 0, 2), B(2, 1, 0) y C(1, 1, 2). Tres puntos no alineados determinan de manera unívoca un plano. Para obtener las ecuaciones paramétricas del plano, necesitamos dos vectores linealmente independientes. Basta tomar los vectores determinados por dos pares distintos de puntos: Tomamos A como punto de referencia y entonces: Ecuaciones paramétricas del plano Eliminamos parámetros: desarrollo por la 1ª columna 2·(x – 1) + 0·y + 1·(z – 2) = 0 2 x + z – 4 = 0 Ecuaciones general del plano

ECUACIONES DEL PLANO EJERCICIO RESUELTO: Halla unas ecuaciones paraméticas del plano : 2 x – 3 y + 3 z – 1 = 0, e indica uno de sus puntos y dos vectores linealmente independientes. Hallar unas ecuaciones paramétricas es equivalente a resolver la ecuación del plano: Despejamos una cualquiera de las variables: Ahora no hay más que asignar un parámetro a x ( ) y otro a z ( ): Ecuaciones paramétricas del plano Teniendo en cuenta los coeficientes de estas ecuaciones, podemos deducir los siguientes elementos del plano: Punto P(0, , 0) Vector u(1, , 0) Vector v(0, 1, 1) En lugar de u también puede tomarse el vector paralelo a él: (3, 2, 0)

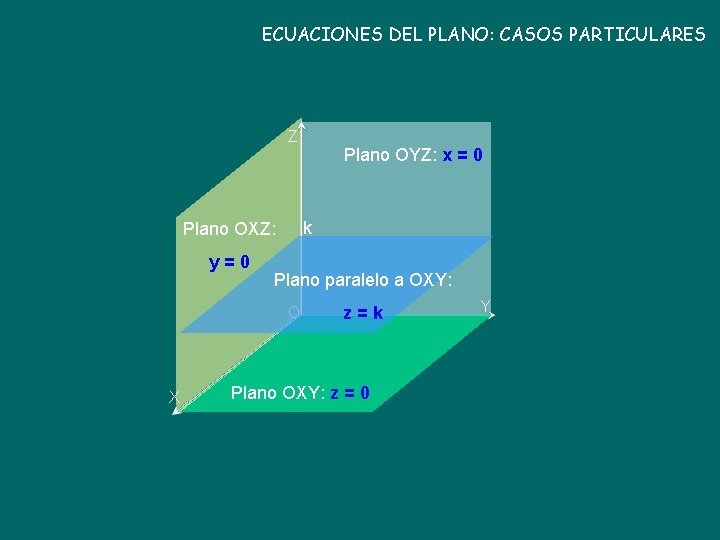
ECUACIONES DEL PLANO: CASOS PARTICULARES Z k Plano OXZ: y=0 Plano paralelo a OXY: O X Plano OYZ: x = 0 z=k Plano OXY: z = 0 Y

POSICIONES RELATIVAS DE UNA RECTA Y UN PLANO Una manera sencilla de estudiar la posición relativa de una recta y un plano es disponer la ecuación del plano en forma general (implícita) y la de la recta en forma paramétrica: : Ax + By + Cz + D = 0 Ahora se sustituyen las expresiones de x, y, z de la recta r, en la ecuación del plano , resultando una ecuación con la única incógnita . Pueden darse tres situaciones: I) Ecuación compatible determinada. Solución única. Recta y plano secantes. II) Ecuación compatible indeterminada. Infinitas soluciones. Recta contenida en el plano. III) Ecuación incompatible. No hay solución. Recta paralela al plano.

POSICIONES RELATIVAS DE UNA RECTA Y UN PLANO Ejemplo 1: Estudia la posición relativa de ls recta r: y el plano : 3 x – y + z = 0. Se sustituyen las expresiones de x, y, z de la recta r, en la ecuación del plano : 3(1 + ) – (– 2 + 2 ) + (3 – ) = 0 3 + 2 – 2 + 3 – = 0 8 = 0 !! Estamos, pues, ante una ecuación incompatible. Así pues, la recta y el plano son PARALELOS Ejemplo 2: Estudia la posición relativa de la recta r: y el plano : 2 x – 2 y + z = 0. Se sustituyen las expresiones de x, y, z de la recta r, en la ecuación del plano : 2(1 – 2 ) – 2(1 + 2 ) + (3 + 5 ) = 0 2 – 4 – 2 – 4 + 3 + 5 = 0 = 1 Ecuación compatible determinada. La recta CORTA al plano en el punto: P(1 2, 1 + 2, 3 + 5), es decir, P( 1, 3, 8)

POSICIONES RELATIVAS DE UNA RECTA Y UN PLANO RECTA Y PLANO DADOS EN FORMA IMPLÍCITA. : A 3 x + B 3 y + C 3 z + D 3 = 0 El estudio de la posición relativa de la recta y el plano equivale a estudiar el sistema de ecuaciones: Así, se consideran las matrices: • r(A) = 3 = r(B) S. C. D. r = P La recta y el plano tienen un punto en común • r(A) = 2; r(B) = 3 S. I. r = Recta y plano son paralelos. • r(A) = 2 = r(B) S. C. I. r = r La recta está contenida en el plano: r Obsérvese que r(A) no puede ser inferior a 2, puesto que entonces no habría recta.

POSICIONES RELATIVAS DE UNA RECTA Y UN PLANO RECTA Y PLANO DADOS EN FORMA PARAMÉTRICA. A(x 1, y 1, z 1) B(x 2, y 2, z 2) u(a, b, c) v(vx, vy, vz) w(wx, wy, wz) Consideramos la matriz cuyas columnas son las componentes de u, v y w: M = (u, v, w) • r(M) = 3 u, v y w son l. i. r = P Recta y el plano tienen un punto en común • r(M) = 2 u depende lin. de v y w Recta y plano son paralelos o bien La recta está contenida en el plano Para resolver la ambigüedad del segundo caso, se comprueba si el punto A está en el plano.

POSICIONES RELATIVAS DE DOS PLANOS Dados los planos: 1: A 1 x + B 1 y + C 1 z + D 1 = 0 y 2: A 2 x + B 2 y + C 2 z + D 2 = 0 Se trata de estudiar el sistema formado por ambas ecuaciones. Por tanto, sean: (I) r(M) = 2 = r(M’) S. C. I. (1 g. l. ) Los planos son SECANTES en una recta r (II) r(M) = 1 = r(M’) S. C. I. (2 g. l. ) Los planos son COINCIDENTES. Obsérvese que r(M’) = 1 significa que: que es una caracterización de los planos coincidentes. (III) r(M) = 1 2 = r(M’) S. I. Los planos son PARALELOS. Esta condición se traduce en que:

POSICIONES RELATIVAS DE DOS PLANOS Ejemplo 1: Estudia la posición relativa de los planos : 2 x + y – z = 0; ’: – 4 x – 2 y + 2 z = 1 Evidentemente r(M) = 1 2 = r(M’) Los planos son PARALELOS Ejemplo 2: Estudia la posición relativa de los planos : x + 3 y – z - 1 = 0; ’: x – 2 y + z = 1 r(M) = 2 = r(M’) Planos SECANTES: recta r: Ejemplo 3: Estudia la posición relativa de los planos : 2 x + 3 y – z = – 1; ’: 4 x – 6 y + 2 z – 2 = 0 r(M) = 1 = r(M’) Planos COINCIDENTES

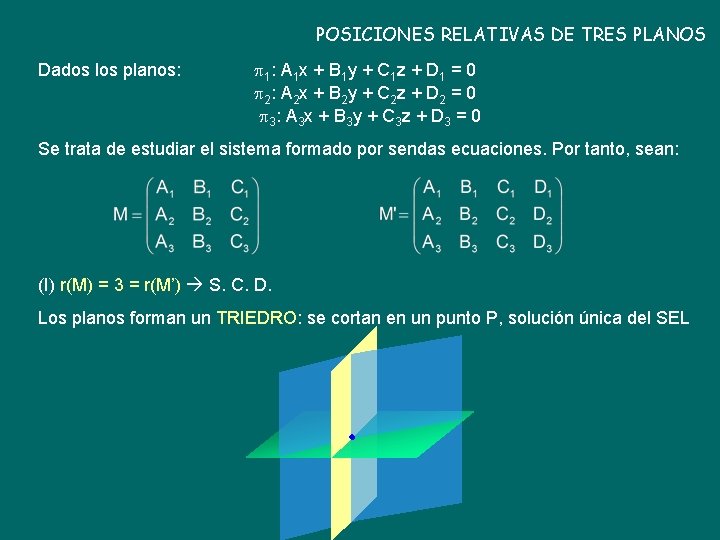
POSICIONES RELATIVAS DE TRES PLANOS Dados los planos: 1 : A 1 x + B 1 y + C 1 z + D 1 = 0 2 : A 2 x + B 2 y + C 2 z + D 2 = 0 3 : A 3 x + B 3 y + C 3 z + D 3 = 0 Se trata de estudiar el sistema formado por sendas ecuaciones. Por tanto, sean: (I) r(M) = 3 = r(M’) S. C. D. Los planos forman un TRIEDRO: se cortan en un punto P, solución única del SEL

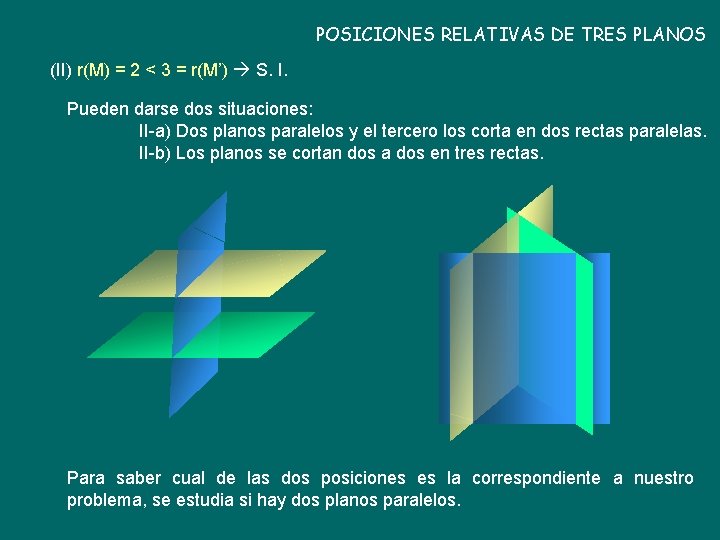
POSICIONES RELATIVAS DE TRES PLANOS (II) r(M) = 2 < 3 = r(M’) S. I. Pueden darse dos situaciones: II-a) Dos planos paralelos y el tercero los corta en dos rectas paralelas. II-b) Los planos se cortan dos a dos en tres rectas. Para saber cual de las dos posiciones es la correspondiente a nuestro problema, se estudia si hay dos planos paralelos.

POSICIONES RELATIVAS DE TRES PLANOS (III) r(M) = 2 = r(M’) S. C. I. (1 g. l. ) Los tres planos tienen una recta en común. Pueden darse dos situaciones: III-a) Dos planos coinciden y el tercero los corta en una recta. III-b) Los planos se cortan los tres en una recta. Para saber cual de las dos posiciones es la correspondiente a nuestro problema, se estudia si hay dos planos coincidentes.

POSICIONES RELATIVAS DE TRES PLANOS (IV) r(M) = 1 < 2 = r(M’) S. I. Pueden darse dos situaciones: IV-a) Tres planos paralelos. IV-b) Dos planos coincidentes y el tercero paralelo. Para saber cual de las dos posiciones es la correspondiente a nuestro problema, se estudian dos a dos para ver si hay dos planos coincidentes. (V) r(M) = 1 = r(M’) S. C. I. (2 g. l. ) Los tres planos son COINCIDENTES

POSICIONES RELATIVAS DE DOS RECTAS Dadas dos rectas r y r’, en cualquiera de las formas en que vengan dadas sus ecuaciones, siempre podremos conseguir un punto y un vector dirección de cada una de ellas. r (A, u) r’ (B, v) Consideraremos un tercer vector w = Sea M la matriz cuyas columnas son las componentes de u y v: M = [u, v] Y sea M’ la matriz cuyas columnas son las componentes de u, v y w: M’ = [u, v, w] (I) r(M) = 1 = r(M’) Los tres vectores tienen la misma dirección. Las dos rectas son COINCIDENTES. (II) r(M) = 1; r(M’) = 2 Los vectores u y v tienen la misma dirección, pero w no. Las rectas son coplanarias PARALELAS (III) r(M) = 2 = r(M’) Los vectores u y v NO tienen la misma dirección, y w es combinación lineal de ellos: Las rectas son coplanarias SECANTES. (IV) r(M) = 2; r(M’) = 3 Los vectores u, v y w son linealmente independientes. Las rectas SE CRUZAN.

POSICIONES RELATIVAS DE DOS RECTAS Ejemplo 1: Estudia la posición relativa de las rectas r A(1, 2, 0), u(1, 1, 3) r’ B( 2, 1, 1), v(2, 1, 3) w( 3, 1, 1) = Puesto que las componentes de u y v no son proporcionales, r(M) = 2. |M’| = 26 0 r(M’) = 3 Las rectas se CRUZAN Ejemplo 2: Estudia la posición relativa de las rectas r A(0, 1, 1), u(1, 2, 1 ) r’ B(0, 2, 2), v(2, 1, 3) w(0, 3, 1) = Puesto que las componentes de u y v no son proporcionales, r(M) = 2. |M’| = 0 r(M’) = 2 Las rectas se CORTAN Para averiguar el punto de corte resolvemos el sistema de ecuaciones: x = x’ = 2 ; y = y’ 1 + 2 = 2 + 1 + 4 = 2 + = 1 = 2 Comprobamos que con estos valores, también z = z’, y entonces P(2, 3, 1)

HACES DE PLANOS HAZ DE PLANOS PARALELOS Dado el plano de ecuación Ax + By +Cz + D = 0, si cambiamos el valor del término independiente D por cualquier número real k, el nuevo plano obtenido es paralelo a . Al conjunto de todos estos planos se le llama haz de planos paralelos a , y la expresión Ax + By + Cz + k = 0 es la ecuación del haz. Ax + By +Cz + kn = 0 Ax + By +Cz + k 2 = 0 Ax + By +Cz + D = 0 Ax + By +Cz + k 1 = 0 Ax + By +Cz + k 3 = 0

HACES DE PLANOS HAZ DE PLANOS SECANTES Sea la recta de ecuaciones implícitas r: Cualquier plano de ecuación (Ax + By + Cz + D) + (A’x + B’y + C’z + D’) = 0 contiene a la recta r puesto que cualquier punto de la recta cumplirá también esta ecuación. Al conjunto de todos los planos que se obtienen para los distintos valores de y se le llama haz de planos secantes de eje la recta r. A efectos prácticos, podemos dividir la expresión por , y llamar = / con lo que la ecuación del haz queda: Ax + By + Cz + D + (A’x + B’y + C’z + D’) = 0 En todo caso, habrá de tenerse en cuenta que en dicha ecuación falta el plano de ecuación A’x + B’y + C’z + D’ = 0 para que el haz quede completo.

HACES DE PLANOS Ejemplo: a) Escribe la ecuación del haz de planos secantes que contienen a la recta r: b) Halla la ecuación del plano de ese haz que pasa por el punto P(2, 1, 1) c) Halla la ecuación del plano de ese haz que pasa por el punto Q(0, 0, 3) a) Ecuación del haz: 2 x + y – z – 1 + (–x + 2 y – z – 3) = 0 b) Para hallar el plano que pasa por P, sustituimos sus coordenadas en la ecuación del haz y despejamos el valor de : 2· 2 + 1 – (– 1) – 1 + [– 2 + 2· 1 – (– 1) – 3] = 0 Entonces, la ecuación del plano es: 2 x + y – z – 1 + 5– 2 =0 = (–x + 2 y – z – 3) = 0 Es decir, simplificando: –x + 12 y – 7 z – 17 = 0 c) Actuamos de manera análoga al apartado anterior: 2· 0 + 0 – (– 3) – 1 + [– 0 + 2· 0 – (– 3) – 3] = 0 2 + 0· = 0 Es decir, no hay ningún valor de que haga que el punto pertenezca al haz. Así pues, la solución será el plano que falta: x + 2 y – z – 3 = 0