REPRESENTACIN GRFICA DE FUNCIONES Ecuaciones paramtricas de una

REPRESENTACIÓN GRÁFICA DE FUNCIONES Ecuaciones paramétricas de una curva plana 1

ECUACIONES PARAMÉTRICAS DE UNA CRUVA PLANA 2

Ecuaciones paramétricas de una curva plana Definición: La parametrización consiste en asociar a cada valor de un parámetro t un punto P(x(t), y(t)) de la curva, de forma que al ir variando t vamos obteniendo los puntos de la curva. y Ecuaciones paramétricas: Campo de existencia de t: P O x Son los valores de t para los cuales existen x(t) e y(t). Se obtienen por intersección de los respectivos dominios de x(t) e y(t). 3

Derivada de una función en forma paramétrica t I Ecuaciones paramétricas de una curva plana: Supongamos que x = x(t) tiene inversa t = x-1(x), es una función continua y derivable en Io I. Luego: y = y(x-1(x)). Derivamos la función “y” aplicando la regla de la cadena se verifica: (Si x’(t) ≠ 0) Otra notación Teorema de la función inversa Sigue 4

Derivada de una función en forma paramétrica Ecuaciones paramétricas de la derivada: 6

Derivada segunda en I 0 Derivada 1ª: Cálculo derivada 2ª: Otra notación 7

Derivada segunda en I 0 Ecuaciones paramétricas de la derivada 2ª: 9

Función vectorial o campo vectorial en R 2 Podemos definir una curva plana como la gráfica de una función: F: D R R 2 t Donde (x(t), y(t)) son las coordenadas del punto P de la curva correspondiente al valor t del parámetro. Este tipo de funciones se llaman funciones vectoriales o campos vectoriales de R en R 2. 10

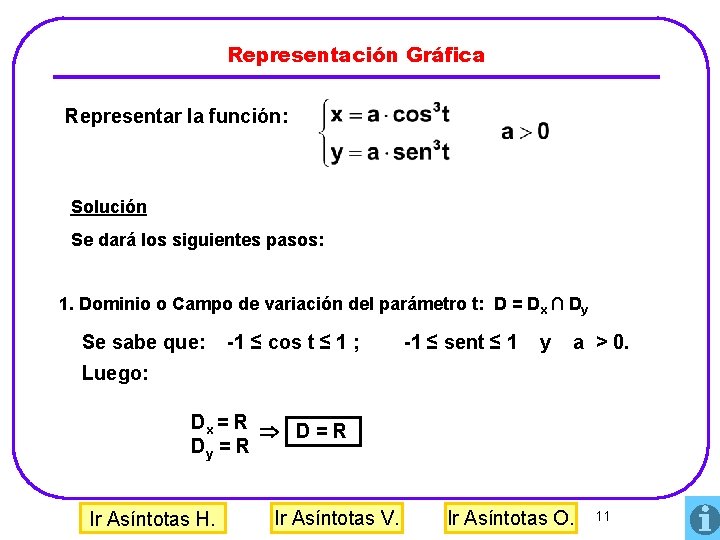
Representación Gráfica Representar la función: Solución Se dará los siguientes pasos: 1. Dominio o Campo de variación del parámetro t: D = Dx ∩ Dy Se sabe que: -1 ≤ cos t ≤ 1 ; -1 ≤ sent ≤ 1 y a > 0. Luego: Dx = R D = R Dy = R Ir Asíntotas H. Ir Asíntotas V. Ir Asíntotas O. 11

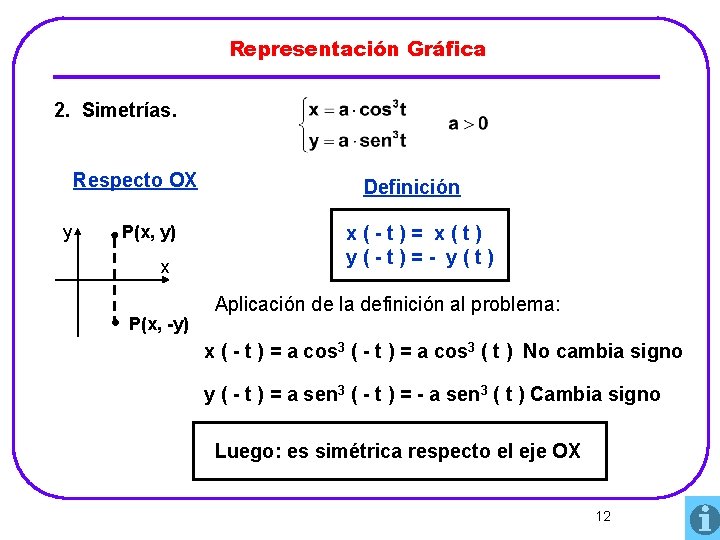
Representación Gráfica 2. Simetrías. Respecto OX y P(x, y) x P(x, -y) Definición x(-t)= x(t) y(-t)=- y(t) Aplicación de la definición al problema: x ( - t ) = a cos 3 ( t ) No cambia signo y ( - t ) = a sen 3 ( - t ) = - a sen 3 ( t ) Cambia signo Luego: es simétrica respecto el eje OX 12

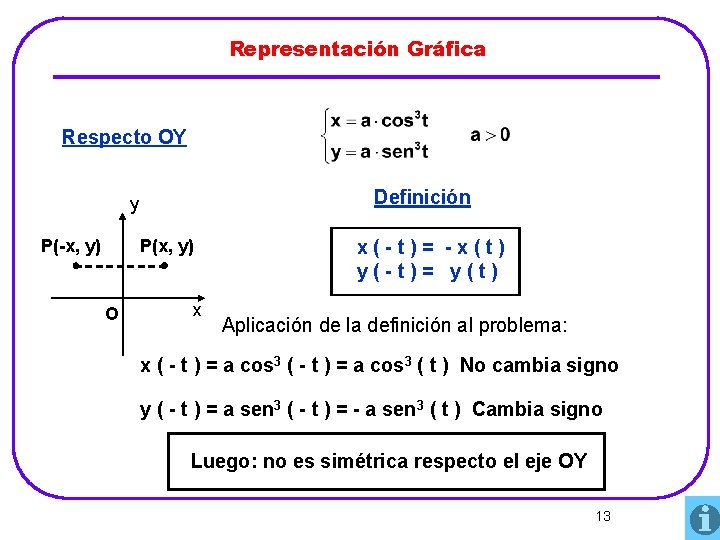
Representación Gráfica Respecto OY Definición y P(x, y) P(-x, y) O x x(-t)= -x(t) y(-t)= y(t) Aplicación de la definición al problema: x ( - t ) = a cos 3 ( t ) No cambia signo y ( - t ) = a sen 3 ( - t ) = - a sen 3 ( t ) Cambia signo Luego: no es simétrica respecto el eje OY 13

Representación Gráfica Respecto del origen O y P(x, y) x Definición x(-t)= - x(t) y(-t)= - y(t) P(- x, - y) Aplicación de la definición al problema: x ( - t ) = a cos 3 ( t ) No cambia signo y ( - t ) = a sen 3 ( - t ) = - a sen 3 ( t ) Cambia signo Luego: no es simétrica respecto al O 14

Periodicidad 3. Periodicidad. Si x e y son funciones periódicas p 1 y p 2 respectivamente, la función vectorial es también periódica de período p = m. c. m de p 1 y p 2 solo hará falta variar t en un intervalo de amplitud p es decir cuando t [a, a + p ]. La elección de “a” dependerá de consideraciones de simetrías aplicables a la curva. Sigue 15

Periodicidad de una función dada Estudio de la periodicidad de la función: x es periódica con período T = 2 π y es periódica con período T = 2 π La curva es periódica con período 2 π ¿Qué intervalo se debe tomar para el estudio de la función? Consideraciones que se debe tener en cuenta: 1. La función es simétrica respecto el eje OX. 2. La amplitud del intervalo es 2π. El intervalo será: [0, π] ya que para t y (–t), las x coinciden. 16

Puntos múltiples Un punto doble o de cruce es aquel que se obtiene para dos valores distintos t 1 y t 2 del parámetro. Se obtiene resolviendo el sistema: Es decir, un punto doble pertenece a dos ramas distintas de la curva Análogamente se define un punto de multiplicidad n 17

Ejemplo de puntos dobles Calcular los puntos dobles de la función: En este caso no hay puntos dobles ya que: t 1 = t 2 Explicación: Solo hay una solución ya que está elevado al cubo. • Con la 1ª ecuación se tiene que cumplir que los + - - + + - cosenos coincidan I y IV cuadrante (ó II y III) • Con la 2ª ecuación, tiene que cumplir que los senos coincidan I y II cuadrante ó (III y IV) Luego como se tiene que cumplir las dos condiciones, solo nos quedamos con una solución. 18

Asíntotas 4. Asíntotas: son rectas tangentes a la función en el infinito. Casos a estudiar: Nota: t 0 puede ser un nº real ó ± a) Horizontal: P( , a) es decir: y A. Horizontal Si x y a Luego: x Entonces: la recta y = a es A. horizontal Aplicación a la curva: Vamos al Dominio de Dx. No hay ningún valor de t que x(t) → 19

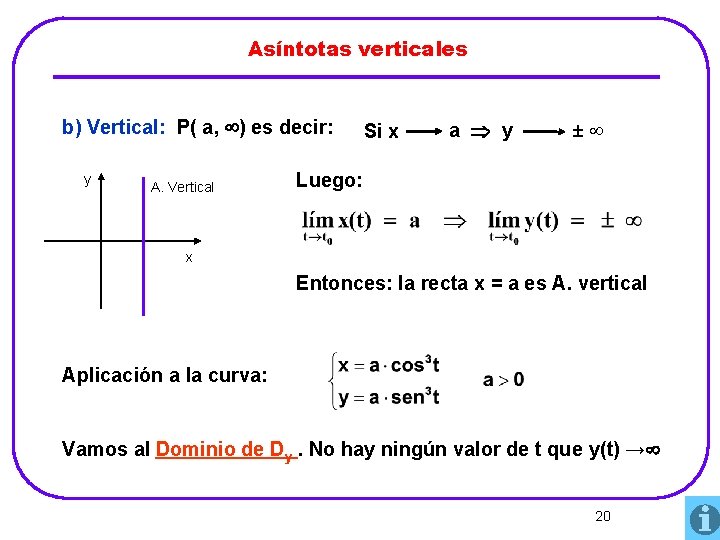
Asíntotas verticales b) Vertical: P( a, ) es decir: y A. Vertical Si x a y ± Luego: x Entonces: la recta x = a es A. vertical Aplicación a la curva: Vamos al Dominio de Dy. No hay ningún valor de t que y(t) → 20

Asíntotas Oblicuas c) Oblicuas: P( , ) es decir: Si x ± y ± Luego: Casos que se pueden presentar: c 1 ) c 2 ) La curva carece de asíntota y se dice que tiene una rama parabólica No hay c 21) Asíntotas c 22) Ecuación: y = m x + n 21

Asíntotas Oblicuas de una curva dada Cálculo de la A. oblicua a la curva: Vamos al Dominio D. No hay ningún valor de t que x (t) → y y(t) → En resumen: La curva dada no tiene Asíntotas. 22

Puntos críticos: Valores del parámetro t que anulan al menos una de las derivadas x’(t), y’(t), o bien alguna de ellas no está definida en t. Ramas de la curva Supongamos que: D = [a, b] y t 1 < t 2 < … < tk son los ptos críticos. Estudiaremos la curva en cada intervalo (ti-1, ti) ya que en este Intervalo x’ es continua y x’(t) ≠ 0 ∀ t x es estrictamente monótona y admite inversa derivable las ecuaciones paramétricas se pueden expresar: y = y(t) = y (x-1 ( t )). Sigue 23

Representación de cada rama Rama x(t) y(t) x’(t) ti-1 < ti valores correspondientes de x valores correspondientes de y signo de x' y’(t) y’x= y’(t)/x’(t) signo de y‘(x) y' Crecimiento de y respecto de x 24

Ejemplo: cálculo de los puntos críticos Cálculo de los puntos críticos da la función: En el intervalo [0, π] • Si x’( t ) = 0 x’(t) = - a · 3 cos 2 t · sen t = 0 • Si y’(t) = 0 y’(t) = a · 3 sen 2 t · cos t = 0 Sigue 25

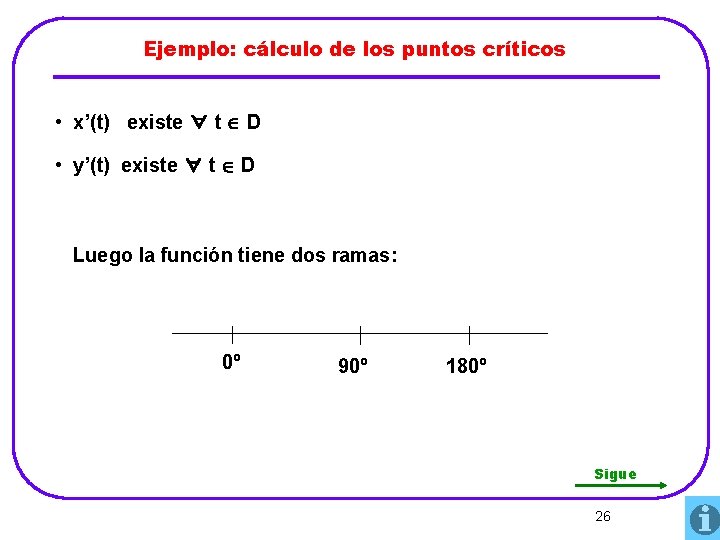
Ejemplo: cálculo de los puntos críticos • x’(t) existe ∀ t D • y’(t) existe ∀ t D Luego la función tiene dos ramas: 0º 90º 180º Sigue 26

Cálculo de los puntos críticos Los puntos críticos de la función: • Si x’( t ) = 0 t = • Si y’(t) = 0 t = son: Dan los mismos resultados 27

Puntos de tangencia vertical Definición de puntos de tangencia vertical para la función: Cálculo de los puntos de tangencia vertical de la función: x’(t) = 0 t = 0º , 90º, 180º estos valores son para los cuales se anula y’(t) No hay puntos de tangencia vertical ya que no cumple la definición. 28

Puntos de tangencia horizontal Definición de puntos de tangencia horizontal para la función: Cálculo de los puntos de tangencia horizontal de la función: y’(t) = 0 t = 0º , 90º, 180º son los mismos valores para los cuales se anula x’(t) No hay puntos de tangencia horizontal ya que no cumplen la definición. 29

Puntos singulares Definición de puntos singulares la función: Cálculo de los puntos de tangencia horizontal de la función: Si hay puntos singulares ya que para t = 0º, 90º, 180º se anula x’(t) e y’(t). Sigue 30

Clasificación de los puntos singulares Notación Llamamos 1. Punto de retroceso de primera especie cuando F’’(t), F’’’(t) no son proporcionales. En el punto, el arco atraviesa a su tangente Sigue 31

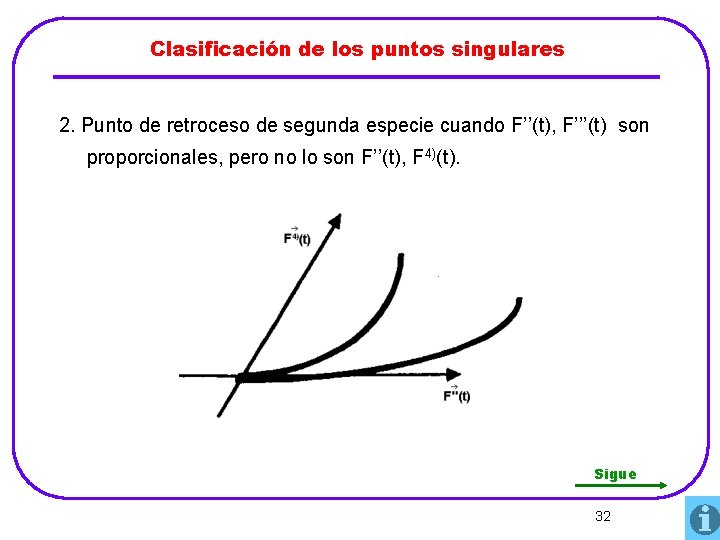
Clasificación de los puntos singulares 2. Punto de retroceso de segunda especie cuando F’’(t), F’’’(t) son proporcionales, pero no lo son F’’(t), F 4)(t). Sigue 32

Ejemplo: estudio de los puntos singulares Estudio de los puntos singulares de la función: En primer lugar se calcula las derivadas siguientes: • x’(t) = - 3 · a · sen t · cos 2 t • x’’(t) = 3 · a · 2 · cos t · sen t + cos t · (- 3 · a · cos 2 t ) = = 6 · a · cos t · sen 2 t - 3 · a · cos 3 t • x’’’(t) = - 6·a·sen t·sen 2 t + 6·a·cos t· 2·cos t·sen t + 9·a·sen t·cos 2 t = = - 6·a ·sen 3 t + 12 · a · sen t · cos 2 t + 9 ·a ·cos 2 t · sen t 33

Ejemplo: estudio de los puntos singulares • y’ (t) = 3 · a · sen 2 t · cos t • y’’(t) = 3 · a · 2 · sen t · cost + 3 · a · sen 2 t · ( - sen t) = = 6 · a ·sen t · cos 2 t - 3 · a · sen 3 t • y’’’(t) = 6·a·sen t· 2·cos t ·(- sen t) +6·a·cos t·cos 2 t – 3·a· 3·sen 2 t·cos t = = - 12 · a · sen 2 t · cos t + 6 · a · cos 3 t – 9 · a · sen 2 t · cos t Sigue 34

Ejemplo: estudio de los puntos singulares Estudio de los puntos singulares: Recordar: 1ª especie si F’’(t) y F’’’(t) no proporcional. 2ª especie si F’’(t), F’’’(t) son proporcionales, pero no lo son F’’(t), F 4)(t). Para t = 0 x’’(0) y’’(0) F’’(0) = (6·a·cos 0º·sen 0º - 3·a·cos 0º, 6·a·sen 0º·cos 0º - 3·a·sen 0º) = (- 3 a , 0) F’’’(0) = (- 6·a ·sen 0º + 12 · a · sen 0º · cos 0º + 9 ·a ·cos 0º · sen 0º , - 12 · a · sen 0º · cos 0º + 6 · a · cos 0º – 9 · a · sen 0º· cos 0º) = = ( 0 , 6 a) NO PROPORCIONALES 1ª especie P(a, 0) 35 Sigue

Ejemplo: estudio de los puntos singulares Para t = 90º F’’(90º) = (6·a·cos 90º·sen 90º-3·a·cos 90º, 6·a·sen 90º·cos 90º-3·a·sen 90º) = ( 0, -3 a) F’’’(90º) = - 6·a ·sen 90º + 12 · a · sen 90º · cos 90º + 9 ·a ·cos 90º · sen 90º, - 12 · a · sen 90º · cos 90º + 6 · a · cos 90º – 9 · a · sen 90º· cos 90º) = = ( - 6 a, 0) F’’(90º) y F’’’(90º) NO SON PROPORCIONALES 1ª especie Cálculo del punto singular: Si t = 90º, sustituyendo en la función: Luego el punto es: P(0, a) 36

Ejemplo: estudio de los puntos singulares Para t = 180º F’’(π) = (6·a·cos π ·sen π -3·a·cos π, 6·a·sen π ·cos π -3·a·sen π) = (3 a, 0) F’’’(π) = - 6·a ·sen π + 12 · a · sen π · cos π + 9 ·a ·cos π · sen π, - 12 · a · sen π · cos π + 6 · a · cos π – 9 · a · sen π · cos π) = = (0, - 6 a) NO PROPORCIONALES 1ª especie Cálculo del punto singular: Si t = 180º, sustituyendo en la función: Luego el punto es: P(-a, 0) Sigue 37

Representación de cada rama Rama 0º<t<90º x(t) a>x>0 90º<t<180º 0>x >-a Cálculos: Si t = 0º x’(t) y’(t) y’x= y’(t)/x’(t) 0< y < a a > y >0 x(0) = a Si t = 0º y(0) = 0 Si t = 90º x(90º) = 0 Si t = 90º y(90º) = a Si t = 180º x(180º) = - a Si t = 180º y(180º) = 0 38

Representación de cada rama Rama 0º<t<90º 90º<t<180º Cálculos: x(t) a>x>0 0>x >-a x’(t) y’(t) - 0< y < a + - x’(t) = - 3 · a · sen t · y’ (t) = 3 · a · sen 2 t · cos t +/-=Decreciente -/-=+ - a > y >0 cos 2 t y’x= y’(t) / x’(t) Creciente _ _ 0º 90º _ + 0º 180º 90º 180º 39

Representación de cada rama y’x= y’(t) / x’(t) Rama x(t) x’(t) y(t) 0º<t<90º a>x>0 - 0< y < a + 90º<t<180º 0>x >-a - a > y >0 - Cálculos de las derivadas y’x, y’’x y’’(x) +/-=Decreciente - -/-= -Creciente + Sigue 40

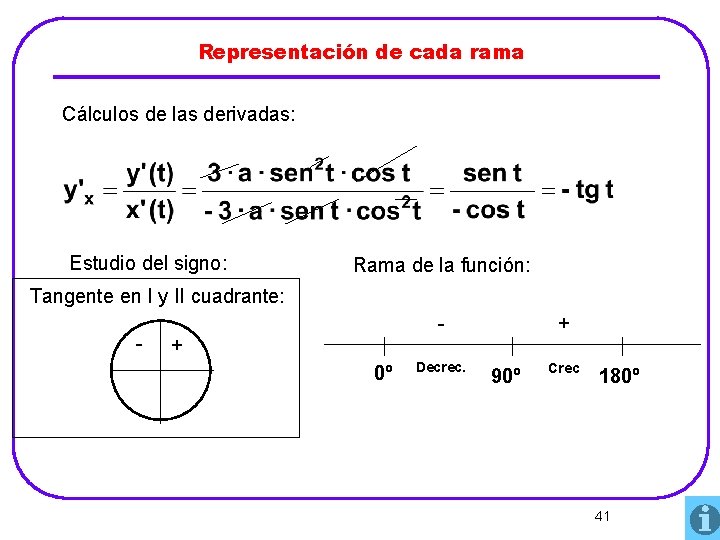
Representación de cada rama Cálculos de las derivadas: Estudio del signo: Rama de la función: Tangente en I y II cuadrante: - - + 0º Decrec. + 90º Crec 180º 41

Representación de cada rama Sustituyendo nos queda: Simplificando, utilizando derive: + = + CÓNCAVA ∀t I , II + + 42

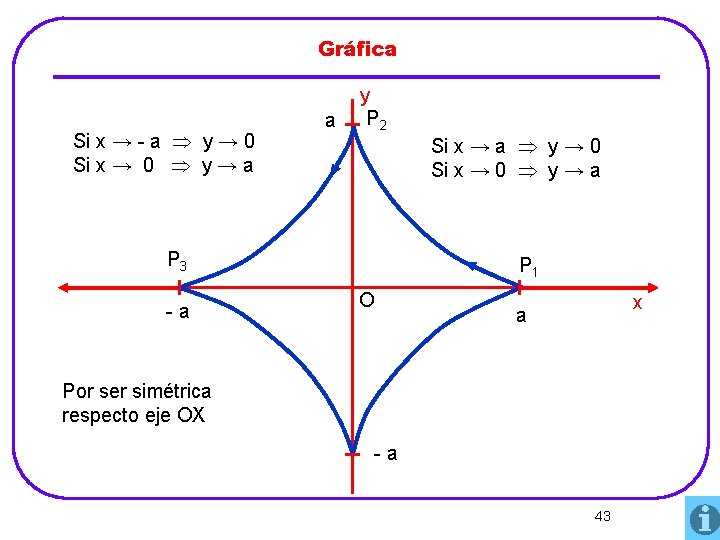
Gráfica Si x → - a y → 0 Si x → 0 y → a a y P 2 P 3 -a Si x → a y → 0 Si x → 0 y → a P 1 O x a Por ser simétrica respecto eje OX -a 43