EANLI DENKLEML MODELLERN ZM YNTEMLER I MATRSSZ ZM

EŞANLI DENKLEMLİ MODELLERİN ÇÖZÜM YÖNTEMLERİ I: MATRİSSİZ ÇÖZÜM: DOLAYLI EKKY 2 AŞAMALI EKKY SINIRLI BİLGİ İLE EÇBY

• Eşanlı denklemli modelin her hangi bir denklemi Basit EKKY ile çözüldüğünde sapmalı, tutarsız tahminler elde edilir. • Geri Dönüşlü Modellerde ise Basit EKKY uygulanabilmektedir. • Bu nedenle eşanlı denklemli modellerin çözümü için farklı yöntemler geliştirilmiştir: 1. Dolaylı EKKY 2. 2 Aşamalı EKKY 3. 3 Aşamalı EKKY gibi…

M denklemli M içsel değişkenli yapısal model : Y 1=a 12 Y 2+a 13 Y 3+…a 1 MYM+b 11 X 1+b 12 X 2+…+b 1 k. Xk+u 1 Y 2=a 21 Y 1+a 23 Y 3+…a 2 MYM+b 21 X 1+b 22 X 2+…+b 2 k. Xk+u 2 Y 3=a 31 Y 1+a 32 Y 2+…a 3 MYM+b 31 X 1+b 32 X 2+…+b 3 k. Xk+u 3 YM=a. M 1 Y 1+a. M 2 Y 2+…a. MMYM-1+b. M 1 X 1+b. M 2 X 2+…+b. Mk. Xk+u. M Denklemlerini tahmin edebilmek için iki yaklaşımdan biri kabul edilir: • Sınırlı bilgi yöntemleri • Tam bilgi yöntemleri

• Sınırlı bilgi yöntemleri(=Tek denklem yöntemleri) Eşanlı denklem sistemlerinin her denklemi, diğer denklemlerden bağımsız şekilde, ferdi olarak tahmin edilir. • Tam bilgi yöntemleri(=sistem yöntemleri) Yapısal denklemlerin tamamı aynı anda çözülür.

Sınırlı bilgi yöntemleri • Dolaylı En Küçük Kareler Yöntemi (=DEKKY) • İki Aşamalı En Küçük Kareler Yöntemi (=2 AEKKY) • Sınırlı Bilgiyle En Çok Benzerlik Yöntemi (=SBEÇBY) Tam bilgi yöntemleri • Üç Aşamalı En Küçük Kareler Yöntemi (3 AEKKY) • Tam Bilgiyle En Çok Benzerlik Yöntemi (=TBEÇBY)

Tam bilgi yöntemlerinin dezavantajları: • Hesaplamalar fazla ve karmaşıktır • Parametrelere göre doğrusal olmayan çözümler vermektedir • Spesifikasyon hatası • sınırlı bilgiye dayalı yöntemler daha kullanışlıdır

Dolaylı En Küçük Kareler Yöntemi (=DEKKY) • Eşanlı modelin yapısal denklemlerini tek çözmeye imkan sağlayan tek denklem yöntemidir. • Tam belirlenmiş yapısal denklemlerin tahmininde kullanılır. • Daraltılmış biçim katsayılarının EKK tahminlerinden yapısal model katsayılarının tahminini elde etmeye dayanır.

Dolaylı EKKY’nin varsayımları • • 1. 2. 3. 4. 5. 6. • Yapısal denklem tam belirlenmelidir. Daraltılmış denklem hata terimi (v) için; Stokastiktir E(vi)=0 Varyansı eşittir Otokorelasyonsuzdur Normal dağılır E(vi. Xj)=0 Dışsal değişkenler arasında çoklu doğrusal bağlantı olmamalıdır

Dolaylı En Küçük Kareler Yöntemi • Adım 1: Daraltılmış biçim denklemleri elde edilir. Daraltılmış katsayılarla ( ) yapısal katsayılar (a, b, c…) arasındaki bağlantılar elde edilir. • Adım 2: Daraltılmış biçim denklemleri ayrı Basit EKKY ile tahmin edilir. • Adım 3: Daraltılmış katsayılar ile yapısal katsayılar arasındaki bağlantılardan yapısal katsayılar hesaplanır.

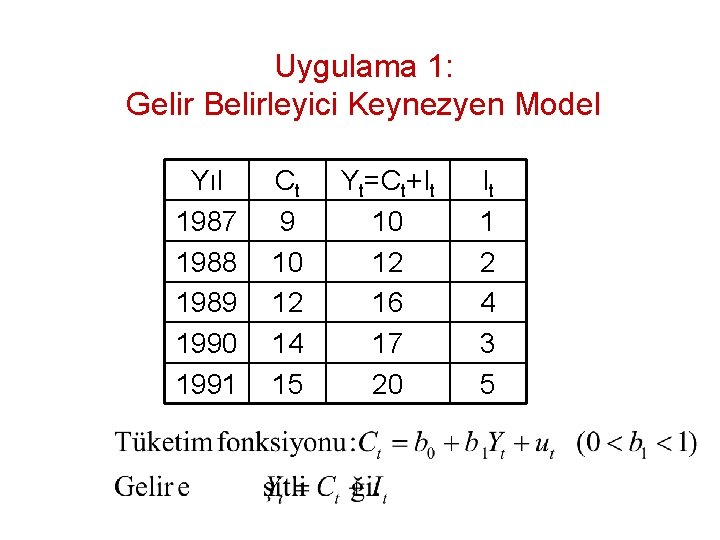
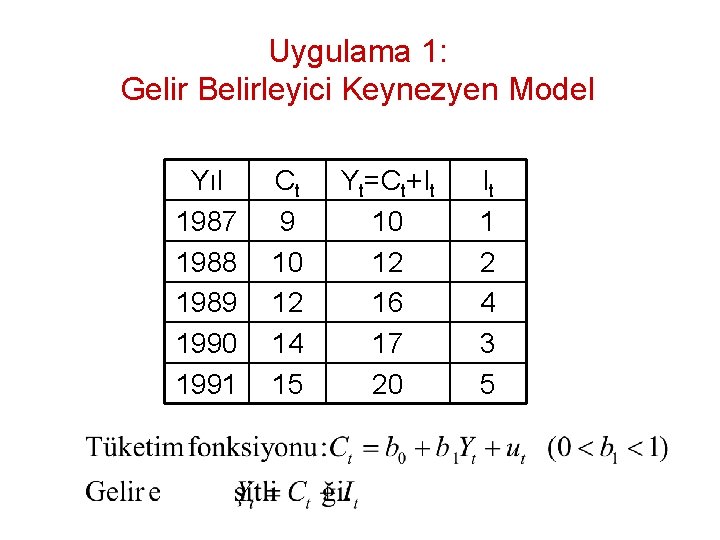
Uygulama 1: Gelir Belirleyici Keynezyen Model Yıl 1987 1988 1989 1990 1991 Ct 9 10 12 14 15 Yt=Ct+It 10 12 16 17 20 It 1 2 4 3 5

Gelir Belirleyici Keynezyen Model • Tüketim fonksiyonu tam belirlendiğine göre Dolaylı EKKY ile tahmin ediniz. 1. Daraltılmış biçim denklemlerinin elde edilişi:

2. Daraltılmış biçim denklemlerinin Basit EKKY ile tahmini

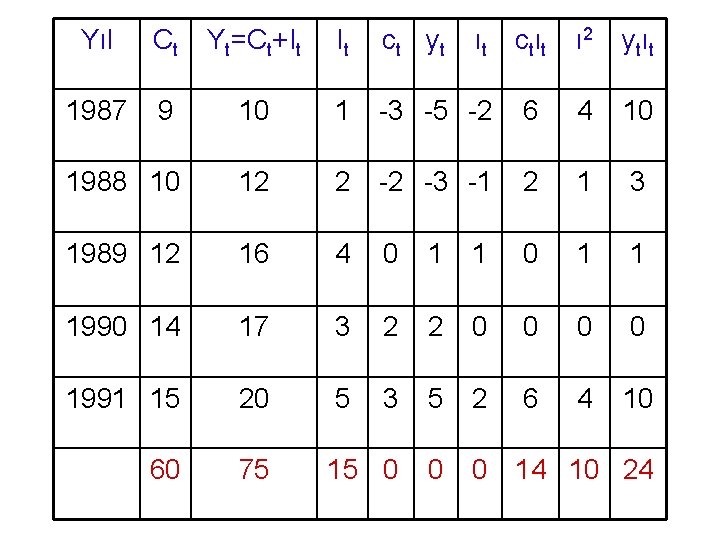
Yıl Ct Yt=Ct+It It ct yt ıt ctıt ı 2 ytıt 1987 9 10 1 -3 -5 -2 6 4 10 1988 10 12 2 -2 -3 -1 2 1 3 1989 12 16 4 0 1 1 1990 14 17 3 2 2 0 0 1991 15 20 5 3 5 2 6 4 10 60 75 15 0 0 0 14 10 24

3. Yapısal Model katsayılarının elde edilmesi:

Yapısal Modelin Tahmini (DEKKYModeli) Marjinal Tüketim Eğilimi Tüketim Modeli Daraltılmış Biçim. Tahmini Kısa Dönem Yatırım Çarpanları

Uygulama 2: Bir Malın Arz-Talep Fonksiyonu Q=Denge arz ve talep miktarı (içsel değişken) P=Malın fiyatı (içsel değişken) I=Tüketicilerin geliri (dışsal değişken) T=Teknoloji seviyesi (dışsal değişken) a 1<0 a 2>0 b 1>0 Her iki denklemde tam belirlenmiştir. Talep ve arz denklemlerini Dolaylı EKKY ile tahminleyiniz.

1. Daraltılmış biçim denklemlerinin elde edilişi: P= 1+ 2 I+ 3 T+v 1 Q= 4+ 5 I+ 6 T+v 2

2. Daraltılmış biçim denklemlerinin Basit EKKY ile tahmini: Daraltılmış Biçim. Tahmini

3. Daraltılmış biçim katsayılarından yapısal katsayıların tahmini:

3. Daraltılmış biçim katsayılarından yapısal katsayıların tahmini: Dolaylı EKK tahminleri: Basit EKK tahminleri:

Dolaylı EKKY Tahmincilerinin Özellikleri • Tutarlı ve asimtotik etkindirler, fakat küçük örneklerde sapmalıdırlar. Yapısal Model Daraltılmış Denklemler P= 1+ 2 I+v 1 Q= 3+ 4 I+v 2

AŞIRI BELİRLENMİŞ BİR DENKLEMİN TAHMİNİ: • İKİ AŞAMALI EN KÜÇÜK KARELER YÖNTEMİ (=2 AEKKY)

İKİ AŞAMALI EN KÜÇÜK KARELER YÖNTEMİ (=2 AEKKY 1. Tahmin edilecek yapısal denklemin sağında yer alan içsel değişkeni bağımlı değişken olarak alan daraltılmış denklem Basit EKKY ile tahminlenir ve bağımlı değişkenin tahmin değerleri hesaplanır. 2. Tahmin edilecek yapısal denklemin sağında yer alan içsel değişken Yi yerine, değişkeni ikame edilerek elde edilen dönüştürülmüş yapısal denkleme Basit EKKY uygulanır.

İKİ AŞAMALI EN KÜÇÜK KARELER YÖNTEMİ • Varsayımları: 1. Tahmin edilecek yapısal denklemin hata terimi u’nun bilinen varsayımları sağlaması gerekir. 2. Daraltılmış biçim hata terimi v bilinen varsayımları sağlamalıdır. 3. Dışsal değişkenler arasında çoklu doğrusal bağlantı olmamalıdır. 4. Dışsal değişkenler bakımından model doğru kurulmuş varsayılmaktadır. 5. Örnek büyüklüğünün yapısal modeldeki dışsal değişken sayısından büyük olması gerekir.

İKİ AŞAMALI EN KÜÇÜK KARELER YÖNTEMİ Adım 1: Yapısal denklemin sağındaki içsel değişken(ler) ile tüm dışsal değişkenler arasındaki daraltılmış regresyon denklem(ler)i Basit EKKY ile tahmin edilir. Yi: İçsel Değişken X: Dışsal Değişken olmak üzere Yi=ai 1 Y 1+ai 2 Y 2+…+ai. MYM+bİ 1 X 1+…+bi. KXK+ui =Genel i. yapısal denklem (tahmin edilecek orijinal yapısal denklem)

İKİ AŞAMALI EN KÜÇÜK KARELER YÖNTEMİ Daraltılmış denklemleri Basit EKKY ile ayrı tahminlenir ve Yi nin tahmin değerleri hesaplanır:

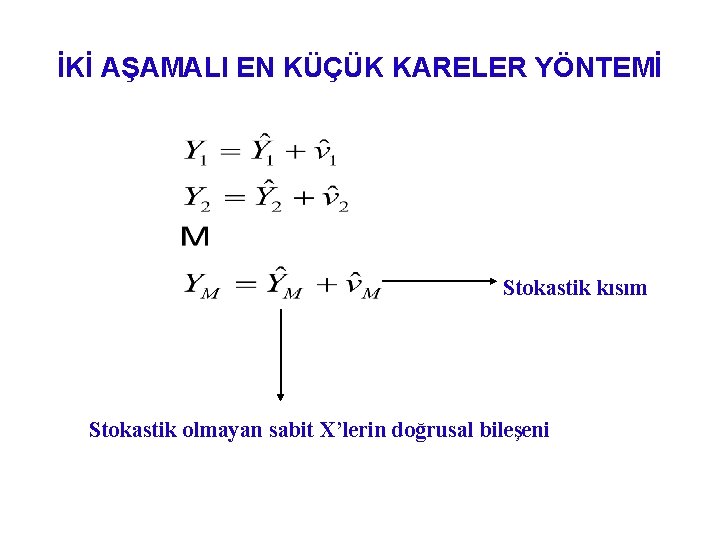
İKİ AŞAMALI EN KÜÇÜK KARELER YÖNTEMİ Stokastik kısım Stokastik olmayan sabit X’lerin doğrusal bileşeni

İKİ AŞAMALI EN KÜÇÜK KARELER YÖNTEMİ Adım 2: İlk adımda hesaplanan değişkenleri yapısal denklemdeki orijinal Y değişkenleri yerine ALET değişken olarak ikame edilir.

İKİ AŞAMALI EN KÜÇÜK KARELER YÖNTEMİ Bu dönüşümlü yapısal denkleme Basit EKKY uygulanarak yapısal parametreler a, b’lerin 2 AEKK tahminleri hesaplanmış olur. ve u* asimtotik olarak ilişkisizdir. Oysa orijinal yapısal denklemde Y’lerle ui’ler ilişkilidir.

Uygulama 1: Gelir Belirleyici Keynezyen Model Yıl 1987 1988 1989 1990 1991 Ct 9 10 12 14 15 Yt=Ct+It 10 12 16 17 20 It 1 2 4 3 5

ADIM 1: Tahmin edilecek orijinal yapısal denklem: C=b 0+b 1 Y+u Denklemin sağında sadece bir tane Y içsel değişkeni vardır, Bu nedenle Basit EKKY ile tahmin edilecek olan daraltılmış denklem şöyledir:

ADIM 2 : İlk aşamada oluşturulan değişkeni orjinal yapısal denklemdeki Y yerine alet değişken olarak alınır.

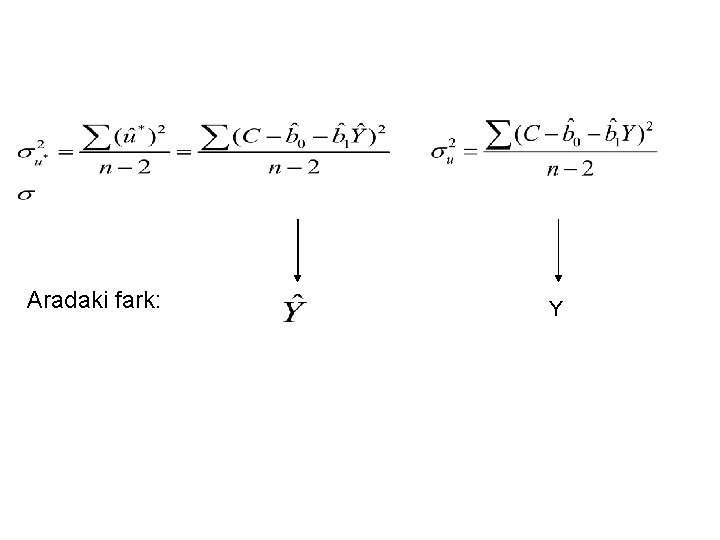
2. AEKK TAHMİNCİLERİNİN HATALARININ TAHMİNİ STANDART 2. AEKKY’nin ikinci aşamasında dönüşümlü yapısal model:

Aradaki fark: Y

Alet Değişken Yöntemi • Tek denklem yöntemidir. • Aşırı belirlenmiş denklemlerin çözümünde daha uygundur. • Tahmin edilecek denklemin sağındaki içsel değişken yerine uygun bir dışsal değişken ikame edilir. • Böylece denklemdeki u hata terimi ile ilişkili içsel değişken ortadan kalkar ve yerine u ile ilişkisi olmayan bir dışsal değişken alet değişken olarak alınır.

ADIM 1 • Yapısal denklemin değişken(ler)in yerine değişken(ler) bulunur. sağında geçecek ADY yer alan uygun alet • Seçilen alet değişken, yapısal denklemde yerine geçeceği içsel değişkenle kuvvetli ilişkili olmalıdır. • Alet değişkenin yapısal denklemdeki dışsal değişkenlerle arasında zayıf ilişki olmalıdır. • Yapısal denklemde birden fazla alet değişken varsa, bunlar arasında zayıf ilişki olmalıdır.

ADIM 2. ADY • Yapısal denklemi ortalamadan sapmalara göre yazarak sabit terimini ortadan kaldırırız. • Her iki tarafı alet değişkeninin ortalamasından farkı ile (ve varsa dışsal değişkenlerin ortalamalarından farkı ile) çarpıp, n gözlem için toplarız. • Yapısal denklemin bilinmeyen sayısı kadar denklem Basit EKKY ile tahminlenir.

ÖRNEK 1 ADY ADIM 1. Tüketim fonksiyonunda Y içsel değişkendir, dışsal değişken yoktur. Y ile u arasında ilişki olduğundan Basit EKKY varsayımları sağlanmamaktadır. Y yerine geçecek bir alet değişken modelin dışsal değişkenleri arasından seçilir. C, I, Y = içsel değişkenler Z 1, Z 2, K = dışsal değişkenler olduğundan Y yerine Z 1 değişkenini alet değişken olarak alabiliriz.

ADIM 2. ADY • Tüketim fonksiyonunu ortalamadan sapmalara göre tekrar yazalım: c=b 1 y+u 1 • Denklemin her iki tarafını z 1 ile çarpıp n gözlem için toplayalım:

ÖRNEK 2 ADY ADIM 1. İki bağımsız değişkenli ikinci modeli ele alıp ADY ile çözelim. Y içsel değişkendir, Z 1 dışsal değişkendir. Y ile u 2 arasında ilişki olduğundan Basit EKKY varsayımları sağlanmamaktadır. Y yerine geçecek bir alet değişken modelin dışsal değişkenleri arasından seçilir. Y=f(Z 1, Z 2, K ) Daraltılmış kalıptan tahmin edilen alabiliriz. değişkenini alet değişken olarak

ADIM 2. ADY Yukarıdaki yapısal denklemi ortalamadan farklara göre yazalım: EKK varsayımı sağlanmamaktadır ve sapma söz konusudur. Bundan kurtulmak için Y yerine değişken olarak alıyoruz. dışsal değişkenini alet

Buradan alet değişken tahmincileri elde edilir.

2 AEKKY ve Alet Değişken Yöntemi (Karşılaştırma) 2 AEKKY • ADIM 1. Y=f(Z 1, Z 2, K) daraltılmış modeli tahmin edilir. Buradan dışsal değişkenlerin değerleri yerine konularak hesaplanır. • ADIM 2. değişkeni (alet değişkeni) Regresyon denkleminde Y yerine ikame edilir. ler

• Dönüşümlü yapısal denklem : Basit EKKY uygulanarak hesaplanan tahminler 2 AEKKY tahminleri olur. Ortalamadan sapmalara göre :

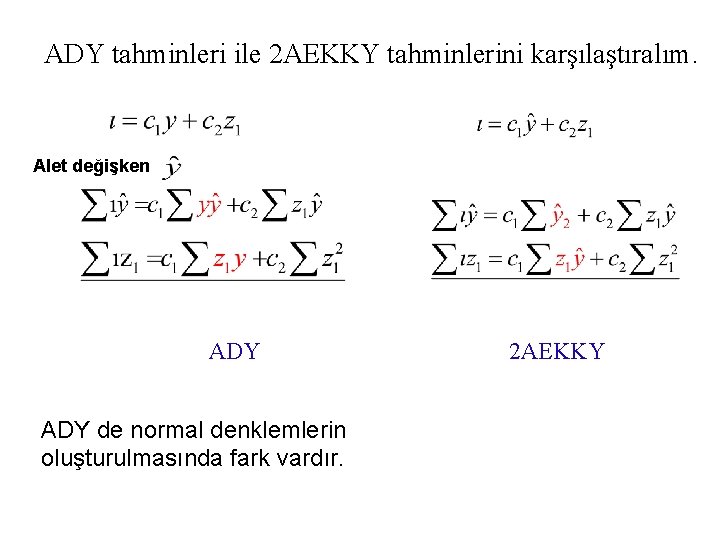
ADY tahminleri ile 2 AEKKY tahminlerini karşılaştıralım. Alet değişken ADY de normal denklemlerin oluşturulmasında fark vardır. 2 AEKKY

İki Aşamalı EKKY Tahminlerinin Özellikleri • 2 AEKKY büyük örnekler için daha uygundur, küçük örneklerde sapmalı tahminler verir. • 2 AEKKY tahminleri tutarlıdır. • 2 AEKKY tahminleri asimtotik etkindirler. • Tam belirlenmiş denklemlerde DEKK ile aynı sonuçları verir. • Aşırı belirlenmiş denklemler için idealdir. • Hesaplanması kolay ve iyi sonuçlar verir. • Dışsal değişkenin çok olduğu durumlarda örnek hacminin fazla olması gereklidir. • Spesifikasyon hatalarına karşı hassastır. • Daraltılmış kalıp denklemlerinin belirlikik katsayıları yüksekse Basit EKK ve 2 AEKK tahminleri birbirine yakın çıkmaktadır.

Eşanlılık Testi Eşanlılık testi, bir açıklayıcı değişkenin (içsel) hata terimi ile ilişkili olup olamadığının testidir. İlişkili ise eşanlılık sorunu vardır. Hausman Model Kurma Testi Talep Fonk. : Qt=a 0+a 1 Pt+a 2 It+a 3 Rt+u 1 t Arz Fonk. : Qt=b 0+b 1 Pt+u 2 t (1) (2) I: Gelir R: Servet Eğer eşanlılık sorunu yoksa (Yani P ile Q karşılıklı bağımsızsa), Pt ile u 2 t ilişkisiz olur. Eğer eşanlılık varsa Pt ile u 2 t ilişkilidir.

Eşanlılık Testi Talep Fonk. : Qt=a 0+a 1 Pt+a 2 It+a 3 Rt+u 1 t Arz Fonk. : Qt=b 0+b 1 Pt+u 2 t (1) (2) Daraltılmış biçim denklemleri: Pt=π0+π1 It+π2 Rt+v 1 (3) Qt=π3+π4 It+π5 Rt+v 2 (4) 1. Adım: Pt nin Rt ile It ye göre regresyonu hesaplanıp ler bulunur. EKKY tahmini (5)

Eşanlılık Sınaması 2. Adım: Qt nin Pt ile ne göre regresyonu hesaplanır: [(5), (2) de yerine konulur] Ho: Eşanlılık yoktur. H 1: Eşanlılık vardır. 3. Adım: v-tah’nin katsayısına t testi uygulanır. Sonuç anlamlı çıkarsa eşanlılık olmadığı hipotezi reddedilir. H 0: Eşanlılık yok H 1: Eşanlılık var

Örnek : Kamu Harcamaları Modeli EXP : Merkezi ve yerel yönetimlerin kamu harcaması AID : Federal yardım düzeyi INC : Eyalet geliri POP : Eyalet nüfusu PS : İlk ve ortaöğretimdeki çocuk sayısı INC , POP , PS : Dışsal değişkenlerdir. ! EXP ve AID arasında eşanlılık çıkma olasılığı vardır…

1. 2. 3. 4. AID’nin INC , POP , PS’ye göre daraltılmış kalıp regresyonu hesaplanır. AID=f(INC, POP, PS) Daraltılmış biçim regresyonundan hata terimlerinin tahminleri hesaplanır. EXP’nin AID , INC , POP’ye göre regresyonu hesaplanır: %5 anlamlılık düzeyinde katsayısı istatistiksel bakımdan anlamlı değildir, dolayısıyla bu düzeyde, eşanlılık sorunu yoktur.

Dışsallık Testi Y 1, Y 2, Y 3 gibi üç değişkenli, üç denklemli bir model ve X 1, X 2, X 3 gibi dışsal değişkenler bulunsun. Y 1 i=b 0+b 2 Y 2 i+b 3 Y 3 i+a 1 X 1 i+u 1 i 1. Adım: Y 2 ve Y 3 için daraltılmış kalıp denklemlerinden Y 2 i-tah ve Y 3 i -tah elde edilir. 2. Adım: Aşağıdaki denklem tahmin edilir. 3. Adım: l 2=l 3=0 hipotezi test edilir. Eğer bu hipotez reddedilirse Y 2 ve Y 3 içsel sayılır.

H 0: l 2=l 3=0 değişkenler dışsaldır H 1: Katsayılardan en az bir tanesi sıfırdan farklıdır. Değişkenler içseldir. Birden fazla katsayının testini Wald F testiyle, tek bir katsayının t testi ile araştırılması gerekmektedir.