Division of Polynomials and Synthetic Division 11599 Division

Division of Polynomials and Synthetic Division 1/15/99 Division of Polynomials by Dave Saha 15 Jan 99

Polynomial Division: Extended Example Divide the polynomial 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 by 3 x 3 – 2 x 2 – 5. Step Set up the division: 3 x 3 – 2 x 2 – 5 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 Step Determine the first partial quotient: 3 x 3 – 2 x 2 – 5 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 6 x 6 = 2 x 3 3 x 3 1/15/99 Division of Polynomials by Dave Saha 2

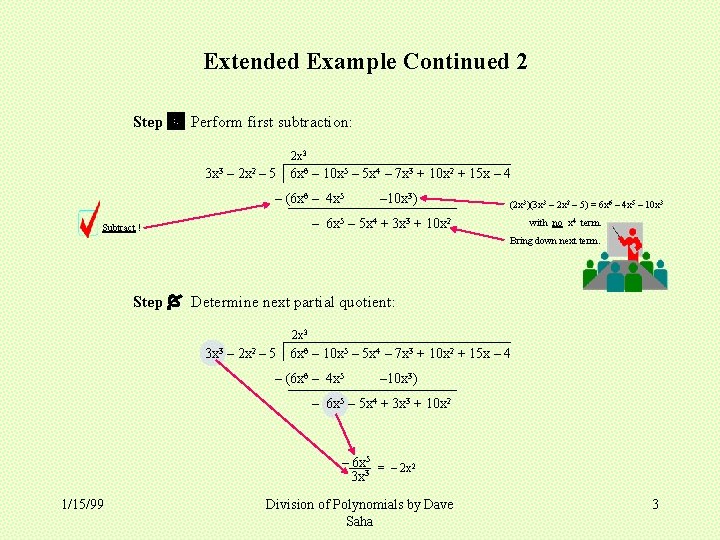
Extended Example Continued 2 Step Perform first subtraction: 2 x 3 3 x 3 – 2 x 2 – 5 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 – (6 x 6 – 4 x 5 – 10 x 3) (2 x 3)(3 x 3 – 2 x 2 – 5) = 6 x 6 – 4 x 5 – 10 x 3 – 6 x 5 – 5 x 4 + 3 x 3 + 10 x 2 Subtract ! with no x 4 term. Bring down next term. Step Determine next partial quotient: 2 x 3 3 x 3 – 2 x 2 – 5 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 – (6 x 6 – 4 x 5 – 10 x 3) – 6 x 5 – 5 x 4 + 3 x 3 + 10 x 2 – 6 x 5 = – 2 x 2 3 x 3 1/15/99 Division of Polynomials by Dave Saha 3

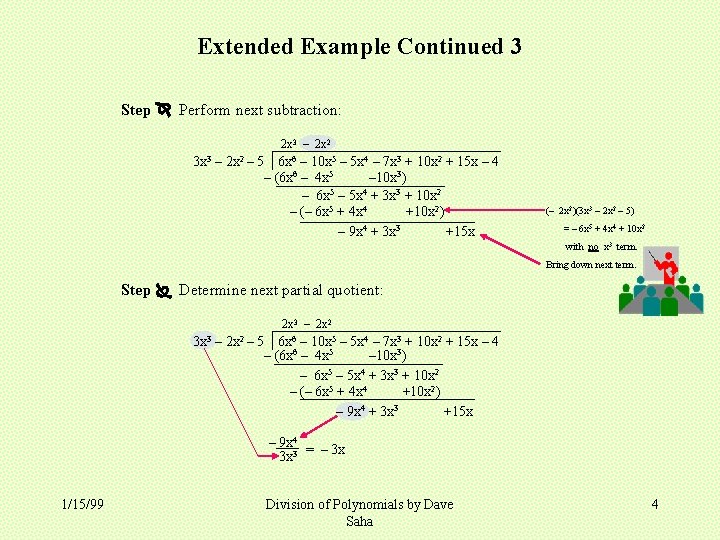
Extended Example Continued 3 Step Perform next subtraction: 2 x 3 – 2 x 2 3 x 3 – 2 x 2 – 5 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 – (6 x 6 – 4 x 5 – 10 x 3) – 6 x 5 – 5 x 4 + 3 x 3 + 10 x 2 – (– 6 x 5 + 4 x 4 +10 x 2) – 9 x 4 + 3 x 3 +15 x (– 2 x 2)(3 x 3 – 2 x 2 – 5) = – 6 x 5 + 4 x 4 + 10 x 2 with no x 3 term. Bring down next term. Step Determine next partial quotient: 2 x 3 – 2 x 2 3 x 3 – 2 x 2 – 5 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 – (6 x 6 – 4 x 5 – 10 x 3) – 6 x 5 – 5 x 4 + 3 x 3 + 10 x 2 – (– 6 x 5 + 4 x 4 +10 x 2) – 9 x 4 + 3 x 3 +15 x – 9 x 4 = – 3 x 3 x 3 1/15/99 Division of Polynomials by Dave Saha 4

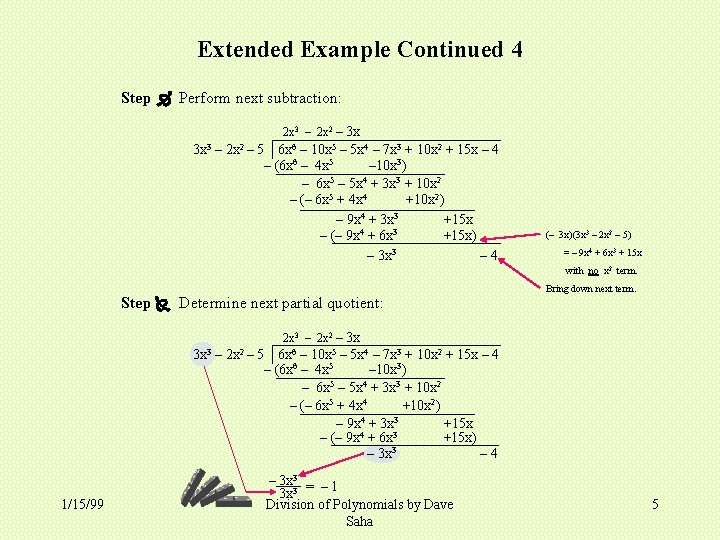
Extended Example Continued 4 Step Perform next subtraction: 2 x 3 – 2 x 2 – 3 x 3 x 3 – 2 x 2 – 5 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 – (6 x 6 – 4 x 5 – 10 x 3) – 6 x 5 – 5 x 4 + 3 x 3 + 10 x 2 – (– 6 x 5 + 4 x 4 +10 x 2) – 9 x 4 + 3 x 3 +15 x 4 3 – (– 9 x + 6 x +15 x) – 3 x 3 – 4 (– 3 x)(3 x 3 – 2 x 2 – 5) = – 9 x 4 + 6 x 3 + 15 x with no x 2 term. Bring down next term. Step Determine next partial quotient: 2 x 3 – 2 x 2 – 3 x 3 x 3 – 2 x 2 – 5 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 – (6 x 6 – 4 x 5 – 10 x 3) – 6 x 5 – 5 x 4 + 3 x 3 + 10 x 2 – (– 6 x 5 + 4 x 4 +10 x 2) – 9 x 4 + 3 x 3 +15 x 4 3 – (– 9 x + 6 x +15 x) 3 – 3 x – 4 1/15/99 – 3 x 3 = – 1 3 x 3 Division of Polynomials by Dave Saha 5

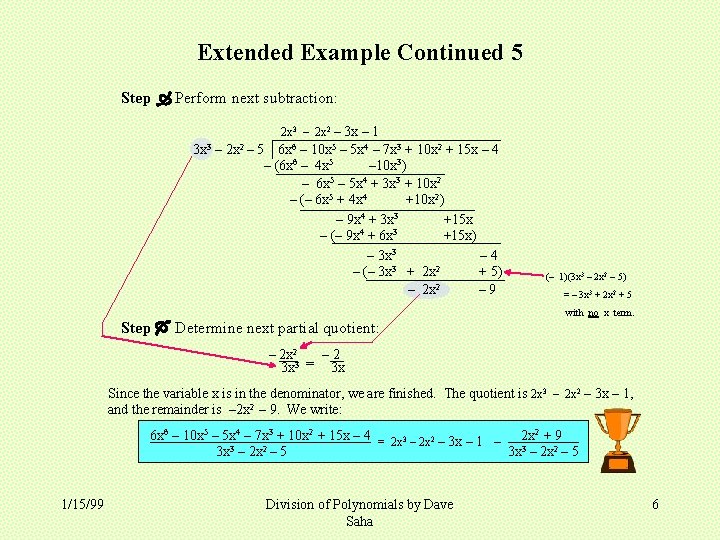
Extended Example Continued 5 Step Perform next subtraction: 2 x 3 – 2 x 2 – 3 x – 1 3 x 3 – 2 x 2 – 5 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 – (6 x 6 – 4 x 5 – 10 x 3) – 6 x 5 – 5 x 4 + 3 x 3 + 10 x 2 – (– 6 x 5 + 4 x 4 +10 x 2) – 9 x 4 + 3 x 3 +15 x 4 3 – (– 9 x + 6 x +15 x) – 3 x 3 – 4 3 2 – (– 3 x + 2 x + 5) 2 – 2 x – 9 (– 1)(3 x 3 – 2 x 2 – 5) = – 3 x 3 + 2 x 2 + 5 with no x term. Step Determine next partial quotient: – 2 x 2 – 2 3 x 3 = 3 x Since the variable x is in the denominator, we are finished. The quotient is 2 x 3 – 2 x 2 – 3 x – 1, and the remainder is – 2 x 2 – 9. We write: 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 = 2 x 3 – 2 x 2 – 3 x – 1 – 2 x 2 + 9 3 x 3 – 2 x 2 – 5 1/15/99 Division of Polynomials by Dave Saha 6

Equations of One Variable OFFICIAL DEFINITIONS • a polynomial function of one variable, x, is of the form f(x) = anxn + an– 1 xn– 1 + + a 0, where an 0, x R, where the exponents must be non-negative integers and the coefficients must be rational. • the degree of a polynomial function of one variable is the highest exponent, n. • a zero of a polynomial of one variable is some value x = k, such that f(k) = 0. That is: ankn + an– 1 kn– 1 + + a 0 = 0 We say that k is a “root” of the equation f(x) = 0. • a polynomial of degree zero is one of the form f(x) = a 0, or simply a constant. R stands for the real numbers. 1/15/99 Division of Polynomials by Dave Saha 7

The Problem We would like to be able to solve any polynomial equation, f(x) = 0, finding all of its roots (all of its zeros). Except for an understanding of what negative numbers are, the general linear case, ax + b = 0, was known by the ancient Greeks: x = – b a The ancient Greeks did most of what we today call algebra by geometric construction, which limited their ability to deal with negative numbers as a concept in themselves. The quadratic case, ax 2 + bx + c = 0, is solved by the quadratic formula: x= –b b 2 – 4 ac 2 a It has been known since the time of the ancient Babylonians! That’s about 1600 B. C. The cubic case, ax 3 + cx + d = bx 2, for positive coefficients a, b, c, and d was solved by the Arabic mathematician Omar Khayyam (better known for has poem, the Rubaiyat) about A. D. 1100, using construction techniques similar to the Greeks. ^ ^ ^ ’Omar ibn Ibrahim al-Khayyami, Giyat ed-din, Abu’l-Fath • 1/15/99 Division of Polynomials by Dave Saha 8

The Next Step Italian mathematicians of the renaissance solved the general cubic and quartic (or -quadratic). bi Nicolo Tartaglia solved the cubic, f(x) = ax 3 + bx 2 + cx + d = 0, in about 1535, in response to a challenge. b Let x = y – 3 a. Then f(x) becomes f´(y) = y 3 + py + q = 0, with no y 2 term. This is called the resolvent equation of f(x); p and q are expressed in terms of a, b, c, and d. A solution of f´(y) = 0 turns out to be y = M + N, where 3 –q ± 2 q 2 p 3 + 4 27 N= 3 –q 2 ± M= q 2 p 3 + 4 27 d 3 r The other solutions are y = – M + N ± i 3 (M – N). UGLY!! 2 2 (This is sometimes called Cardano’s formula, after Girolamo Cardano, who published it first in 1545. Tartaglia kept it secret; it’s one of the great stories in the history of math. ) Shortly after, by about 1540, Ludovico Ferrari solved the quartic (or bi-quadratic), ax 4 + bx 3 + cx 2 + dx + e = 0, using methods similar to Tartaglia. Ferrari reduced the 4 th degree equation to its resolvent cubic, then used Cardano’s formula. 1/15/99 Division of Polynomials by Dave Saha 9

The Last Step About 280 years after, in 1824, Niels Henrik Abel published the first disproof in all of history. He proved that a general formula to solve ax 5 + bx 4 + cx 3 + dx 2 + ex + f = 0, the quintic equation, was impossible! Further, from the work of Evariste Galois, in 1830 to 1832, developed an understanding of why there can be no quintic or higher formula. For a formula to exist to solve f(x) = 0 for some degree, there must be symmetry among the zeros. In the case of the quadratic, the symmetry is simple. In the cases of the cubic and quartic, the symmetry is more complex, but the arithmetic operations of the formulae help impose the necessary order. For the quintic and higher order polynomials, the symmetry is just not present, except in special cases, and cannot be imposed! So pat formulae to solve equations of one variable turns out to be a dead end. Consequently, modern mathematics uses very different methods…. 1/15/99 Division of Polynomials by Dave Saha 10

The Modern Approach to f(x) = 0 • the Fundamental Theorem of Algebra: Every polynomial of degree at least one has at least one complex zero. First proved by Carl Friederich Gauss in 1799, as his doctoral thesis, the most important part of this theorem for our purposes is that the zero of the function exists and is nothing more complicated than a complex number. A direct consequence of the fundamental theorem of algebra is this: A polynomial of degree n has at most n distinct zeros. In other words, a polynomial f(x) = 0 of degree n has n solutions. Some of these solutions may be the same, for example a polynomial which has zeros x = 3, and x = 3. In such a case, the zero of the polynomial is said to have a multiplicity. 1/15/99 Division of Polynomials by Dave Saha 11

The Modern Approach 2 Now we would like to know if x = k is a solution (root or zero) of f(x) = 0. Division of polynomials is similar to simple division of numbers: f(x) r(x) = q(x) + x–k or f(x) = q(x) • (x – k) + r(x) But the degree of r(x) must be held to an important condition: 0 degree[ r(x) ] degree[ x – k ] Since the degree of x – k is one, we conclude that the degree of r(x) must be zero, which means the remainder is just a constant, r(x) = r. Thus we have f(x) = q(x) • (x – k) + r But we also know that if x = k is a zero of the polynomial that f(k) = 0. I knew this was leading somewhere. f(k) = q(k) • (k – k) + r = 0 q(k) • (0) + r = 0 r=0 1/15/99 Division of Polynomials by Dave Saha 12

The Factor Theorem • We have just shown an important result, know as the Factor theorem: (x – k) is a factor of polynomial f(x) if and only if (x – k) is a zero of f(x), and f(k) = 0. Okay, we know that f(x) = 0 has n zeros, where n is the degree of f(x). Are the zeros of the polynomial rational, real, or complex? Are they positive or negative? If we label the zeros of f(x) as k 1, k 2, k 3, … , kn, then we can write f(x) = anxn + an– 1 xn– 1 + + a 0 = an(x – k 1)(x – k 2)(x – k 3) (x – kn) If we start with simple cases, f(x) = ax 2 + bx + c = a(x – k 1)(x – k 2) and analyze the possibilities, we discover a rule connecting the algebraic sign of the zeros, x = k 1 and x = k 2, and the pattern of signs of the coefficients a, b, and c in f(x). • This result is known as Decarte’s Rule of Signs: Let f(x) be a polynomial with real coefficients. (a) The number of positive real zeros of f(x) is equal to the number of variations of sign of the coefficients of f(x). (b) The number of negative real zeros of f(x) is equal to the number of variations of sign of the coefficients of f(–x). 1/15/99 Division of Polynomials by Dave Saha negati ve positive i-axis Decarte’s road sign 13

Decarte’s Rule of Signs There is a necessary modification to theorem as stated above, but we will get to that in a little bit. The important thing now is to get used to what it means. DECARTE’S RULE OF SIGNS: Let’s look at the example of variation of signs: f(x) = 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 As indicated by the arrows, there are three places in the polynomial where the coefficients switch either from positive to negative, or negative to positive. The leading coefficient, 6, is positive; remember that we don’t usually write an explicit plus sign for initial numbers that are positive. Thus this polynomial has three zeros that are positive real numbers, according to part (a) of theorem. Now substitute (–x) for x: f(–x) = 6(–x)6 – 10(–x)5 – 5(–x)4 – 7(–x)3 + 10(–x)2 + 15(–x) – 4 = 6 x 6 + 10 x 5 – 5 x 4 + 7 x 3 + 10 x 2 – 15 x – 4 As indicated by the arrows, there are three places in the polynomial f(–x) where the coefficients switch either from positive to negative, or negative to positive. Thus the original polynomial, f(x), has three zeros that are negative real numbers, according to part (b) of theorem 1/15/99 Division of Polynomials by Dave Saha 14

The Rest of the Roots In the example, f(x) = 6 x 6 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4, all six zeros of the polynomial are counted by Decartes’s Rule. There are many cases where all the zeros will not be counted. Consider f(x) = x 30 – 10 x 5 – 5 x 4 – 7 x 3 + 10 x 2 + 15 x – 4 f(– x) = x 30 + 10 x 5 – 5 x 4 + 7 x 3 + 10 x 2 – 15 x – 4 3 positive real zeros 3 negative real zeros Only six zeros are counted this way; where are the other twenty-four? They exist, but are not real numbers; rather, they are complex numbers. Ah! That’s why we had to learn that stuff. 1/15/99 Division of Polynomials by Dave Saha 15

Complex Conjugate Zeros • A direct result of the properties of complex conjugates is this, the Complex Conjugate theorem: if a + bi is a zero of f(x), then so is its conjugate, a – bi. Now look at f(x) = x 2 + x + 1 no positive real roots f(–x) = x 2 – x + 1 2 negative real roots The only problem is that the zeros of this polynomial are complex, as may be shown with the quadratic formula: x = – 1 1 2– 4(1)(1) – 3 = – 1 2 2 The fact is that i 2 gives Decarte’s Rule problems. Since the Complex Conjugate theorem is a more important result, it take precedence. We modify Decarte’s Rule of Signs: Let f(x) be a polynomial with real coefficients. (a) The number of positive real zeros of f(x) is equal to the number of variations of the signs of the coefficients of f(x) or less than that number by a positive even number. (b) The number of negative real zeros of f(x) is equal to the number of variations of the signs of the coefficients of f(–x) or less than that number by a positive even number. 1/15/99 Division of Polynomials by Dave Saha 16

The Rational Zeros Theorem • Rational Zeros theorem: If a zero of the polynomial f(x) = anxn + an– 1 xn– 1 + + a 0, with integer coefficients, is rational, p/q, then p must be a factor of the constant term, a 0, and q must be a factor of the leading coefficient, an. This is easy to show. Remember that a polynomial may be expressed as the product of all its zeros: f(x) = anxn + an– 1 xn– 1 + + a 0 = an(x – k 1)(x – k 2)(x – k 3) (x – kn) a a xn + an– 1 xn– 1 + + a 0 = (x – k 1)(x – k 2)(x – k 3) (x – kn) n n If we multiply all the binomials on the right, we get constant. a k 1 k 2 k 3 kn = a 0 n for the If any ki is rational, p/q, then the rest of the kj multiplied together = implies theorem. 1/15/99 Division of Polynomials by Dave Saha qa 0 , which pan 17

Example of the Rational Zeros Theorem Choose x = 1 , x = 2 , and x = – 5 : 2 3 2 f(x) = 12 x 3 + 16 x 2 – 31 x + 10 f(– x) = – 12 x 3 + 16 x 2 + 31 x + 10 2 positive real zeros 1 negative real zero The constant term is 10, with factors 1, 2, 5, 10. The leading coefficient is 12, with factors 1, 2, 3, 4, 6, 12. The list of possible rational zeros of this polynomial is quite long: 1 1 1 = 1 2 = 1 2 = 2 2 12, 6, 4, 3, 2, 1 , 12 6 , 6 3, 4 2 , 1 , 3, 5 5 5 = 5 10 10 10 = = 5 = 10 12, 6, 4, 3, 2, 1 , 12 6 , 6 3 , 4 2 , 1 , 3. Notice that the actual zeros are among the rational zeros listed (the heavy underlines, Now, if there was only a quick way to test these values! 1/15/99 Division of Polynomials by Dave Saha ). 18

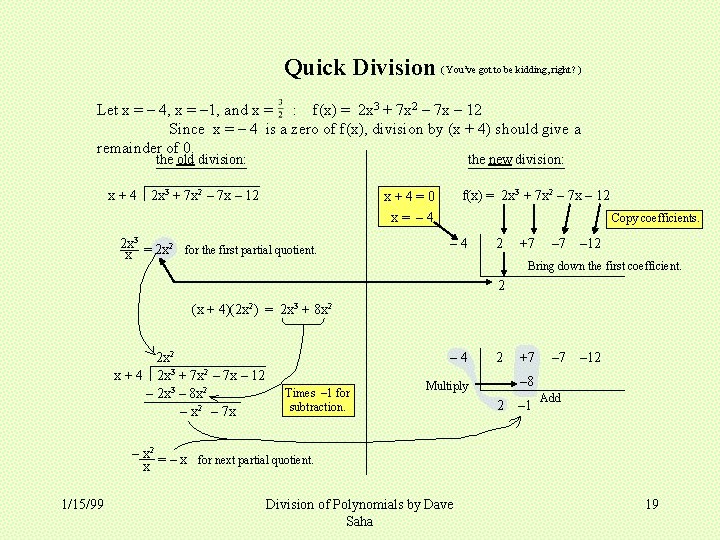
Quick Division ( You’ve got to be kidding, right? ) Let x = – 4, x = – 1, and x = : f(x) = 2 x 3 + 7 x 2 – 7 x – 12 Since x = – 4 is a zero of f(x), division by (x + 4) should give a remainder of 0. the old division: x+4 the new division: 2 x 3 + 7 x 2 – 7 x – 12 f(x) = 2 x 3 + 7 x 2 – 7 x – 12 x+4=0 x= – 4 2 x 3 = 2 x 2 for the first partial quotient. x Copy coefficients. – 4 2 +7 – 12 Bring down the first coefficient. 2 (x + 4)(2 x 2) = 2 x 3 + 8 x 2 2 x 2 x + 4 2 x 3 + 7 x 2 – 7 x – 12 – 2 x 3 – 8 x 2 – 7 x – 4 Times – 1 for subtraction. 2 +7 – 12 – 8 Multiply 2 – 1 Add – x 2 = – x for next partial quotient. x 1/15/99 Division of Polynomials by Dave Saha 19

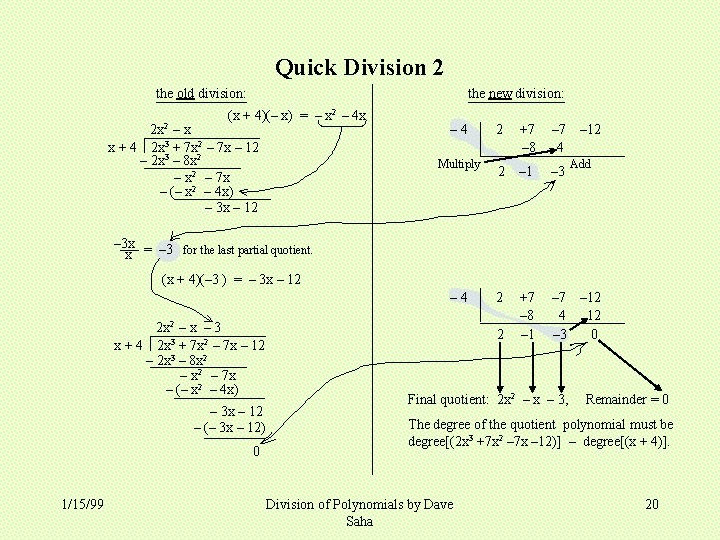
Quick Division 2 the old division: the new division: (x + 4)(– x) = – x 2 – 4 x 2 x 2 – x x + 4 2 x 3 + 7 x 2 – 7 x – 12 – 2 x 3 – 8 x 2 – 7 x – (– x 2 – 4 x) – 3 x – 12 – 4 Multiply 2 +7 – 8 – 7 4 – 12 2 – 1 – 3 2 +7 – 8 – 1 – 7 – 12 4 12 – 3 0 Add – 3 x = – 3 for the last partial quotient. x (x + 4)(– 3 ) = – 3 x – 12 – 4 2 x 2 – x – 3 x + 4 2 x 3 + 7 x 2 – 7 x – 12 – 2 x 3 – 8 x 2 – 7 x – (– x 2 – 4 x) – 3 x – 12 – (– 3 x – 12) 0 1/15/99 2 Final quotient: 2 x 2 – x – 3, Remainder = 0 The degree of the quotient polynomial must be degree[(2 x 3 +7 x 2 – 7 x – 12)] – degree[(x + 4)]. Division of Polynomials by Dave Saha 20

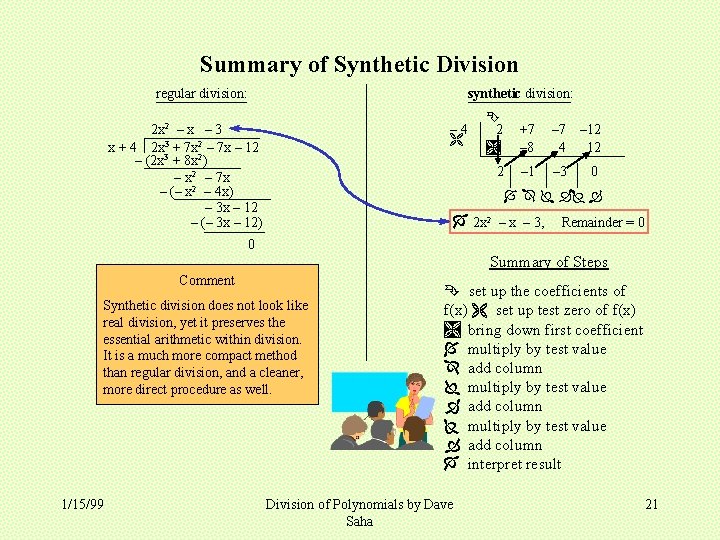
Summary of Synthetic Division regular division: synthetic division: 2 x 2 – x – 3 x + 4 2 x 3 + 7 x 2 – 7 x – 12 – (2 x 3 + 8 x 2) – x 2 – 7 x – (– x 2 – 4 x) – 3 x – 12 – (– 3 x – 12) – 4 2 +7 – 8 – 7 4 – 12 12 2 – 1 – 3 0 2 x 2 – x – 3, Remainder = 0 0 Summary of Steps Comment Synthetic division does not look like real division, yet it preserves the essential arithmetic within division. It is a much more compact method than regular division, and a cleaner, more direct procedure as well. 1/15/99 set up the coefficients of f(x) set up test zero of f(x) bring down first coefficient multiply by test value add column interpret result Division of Polynomials by Dave Saha 21

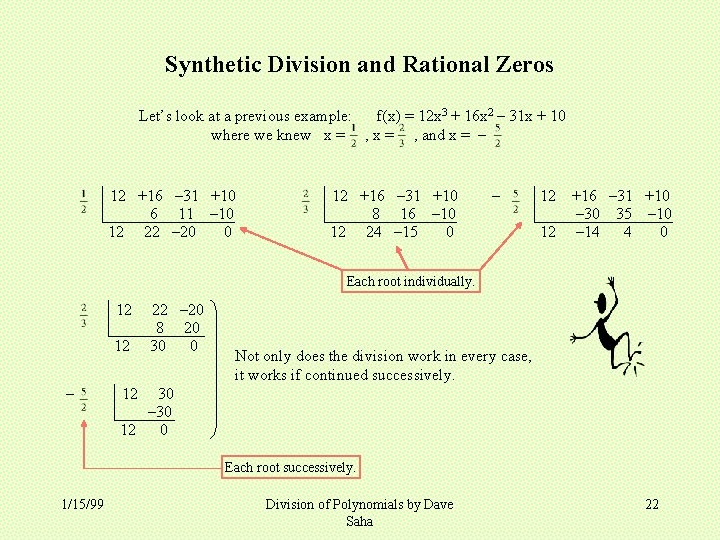
Synthetic Division and Rational Zeros Let’s look at a previous example: f(x) = 12 x 3 + 16 x 2 – 31 x + 10 where we knew x = , and x = – 12 +16 – 31 +10 6 11 – 10 12 22 – 20 0 12 +16 – 31 +10 8 16 – 10 12 24 – 15 0 – 12 +16 – 31 +10 – 30 35 – 10 12 – 14 4 0 Each root individually. 12 12 – 20 8 20 30 0 Not only does the division work in every case, it works if continued successively. 12 30 – 30 12 0 Each root successively. 1/15/99 Division of Polynomials by Dave Saha 22

Synthetic Division and the Factor Theorem For the example: f(x) = 2 x 3 + 7 x 2 – 7 x – 12 the Rational Zero theorem gives these possible zeros of the polynomial: x = , 1, , 2, 3, 4, 6, 12 What if we wanted to test x = – 2 ? – 2 2 The division shows the remainder is not zero, so x = – 2 is not a zero and x + 2 is not a factor. 2 What if we wanted to test x = 2 ? The division shows the remainder is not zero, so x = is not a zero and x – is not a factor. What if we wanted to test x = + 2 ? The division shows the remainder is not zero, so x = +2 is not a zero and x – 2 is not a factor. 2 2 +7 – 12 – 4 – 6 26 3 – 13 14 +7 1 8 – 7 – 12 4 – – 3 – 13 +7 4 11 – 7 – 12 22 30 15 18 The Rational Zero theorem, the Factor theorem, and Synthetic Division are the quick method desired, by which we may find and test all possible rational zeros. 1/15/99 Division of Polynomials by Dave Saha 23

Synthetic Division and Complex Zeros For example: f(x) = x 3 – 5 x 2 + 11 x – 15 This was generated by choosing x = 1 – 2 i, x = 1 + 2 i, and x = 3. We know that x = 3 will work. What if we test x = 1 – 2 i ? And x = 1 + 2 i, to be complete: 3 1 1 – 2 i 1 1 + 2 i – 5 3 1 – 2 11 – 6 5 – 15 15 0 – 5 11 – 15 1 – 2 i – 8 + 6 i 15 1 – 4 – 2 i 3 + 6 i 0 1 – 5 11 – 15 1 + 2 i – 8 – 6 i 15 1 – 4 + 2 i 3 – 6 i 0 Synthetic Division works with complex numbers as zeros of a polynomial! 1/15/99 Division of Polynomials by Dave Saha 24

One Last Note: Be Careful! Align your columns to avoid problems. Let f(x) = x 5 – 3 x 3 – 9 x + 10. If you do not include columns for the missing x 4 and x 2 terms, the division will not work correctly. This example was designed for x = 2 to be a zero of the polynomial. INCORRECT: 2 1 1 – 3 2 – 1 – 9 – 2 – 11 + 10 – 22 – 12 0 2 2 – 3 4 1 0 2 2 Potential! – 9 4 – 5 +10 – 10 0 f(2) = (2)5 – 3(2) 3 – 9(2) + 10 = 32 – 24 – 18 + 10 = 0. 1/15/99 Division of Polynomials by Dave Saha 25