Division Short Division Long Division Key Vocabulary Key

Division Short Division Long Division Key Vocabulary

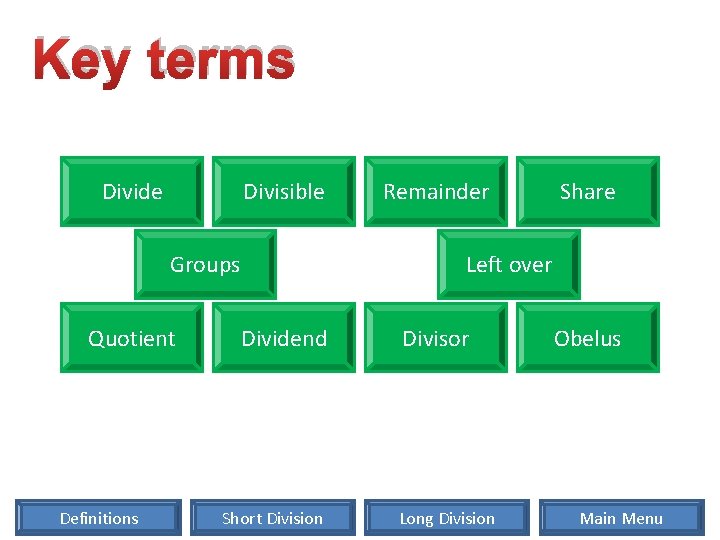
Key terms Divide Divisible Groups Quotient Definitions Remainder Share Left over Dividend Short Division Divisor Long Division Obelus Main Menu

Definitions Divide To Divide is to share or group a number into equal parts. Eg) If you divide 10 by 2 you get 5. Divisible A number is divisible if it can be divided without a remainder. Eg) 10 can be divided by 2, it is divisible by 2. 10 can not be divided by 3 without a remainder so 10 is not divisible by 3. Remainder A remainder is the amount left over after dividing a number. Eg) If you divide 10 by 3 the answer is 2 with 1 remainder Share Groups To share is to divide into equal groups. Eg) If you share 10 sweets between 2 people, each person gets 5. Grouping is the process of dividing into equal sets (groups). Eg) If you share 10 sweets between 2 people, each person gets 5. Left over The left over is the same as the remainder. Eg) If you divide 10 by 3, the answer is 3 with 1 left over. Quotient The Quotient is the number resulting from dividing one number by another (the answer) Eg) In 10 ÷ 5 = 2, the quotient is 2. Dividend The Dividend is the number being divided. Eg) In 10 ÷ 5 = 2, 10 is the dividend. Divisor The Divisor is the number you are dividing by. Eg) In 10 ÷ 5 = 2, 5 is the divisor is the dividend. Obelus The Obelus is the name of the ÷ sign. Short Division Long Division Main Menu

Short Division What is division? Reversing Multiplication Repeated subtraction Working with remainders The Bus Stop Method The Grid Method Definitions Long Division Main Menu

Short Division What is division? Division is a Mathematical Operation (like add, subtract and multiply). Division determines how many times one quantity is contained in another. It is the inverse of multiplication. Mathematical Operations include: Divisions can be written in many different ways 261 ÷ 3 Definitions 261 3 3 261 Long Division Main Menu

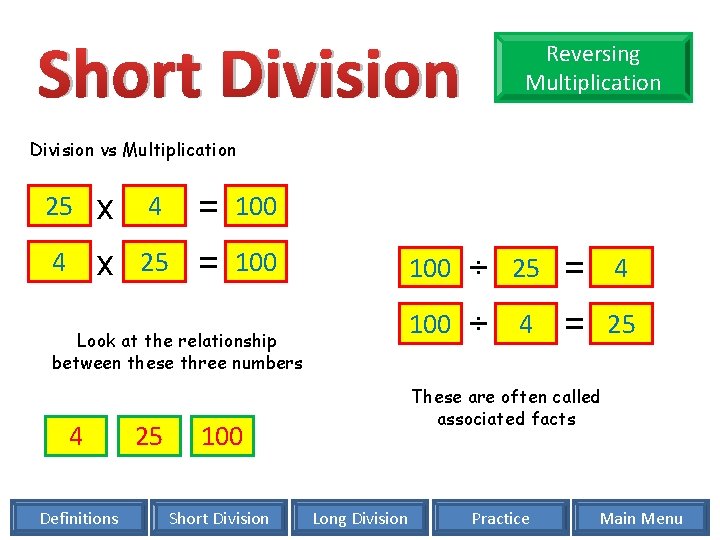
Short Division Reversing Multiplication Division vs Multiplication 25 x 4 = 100 4 x 25 = 100 Look at the relationship between these three numbers 4 Definitions 25 ÷ 25 = 4 100 ÷ 4 = 25 These are often called associated facts 100 Short Division 100 Long Division Practice Main Menu

Short Division This is called the bus stop method. See the resemblance? 3 3 The Bus Stop Method 2 1 9 6 3 To work out this sum, divide 963 by 3, one digit at a time, starting from the left. This is sometimes called the space saver method Definitions Short Division Long Division Practice Main Menu

Short Division The Bus Stop Method 0 4 6 2 4 1 2 5 2 To work out this sum, divide 252 by 3, one digit at a time, starting from the left. Definitions Short Division Long Division Practice Main Menu

Short Division The Bus Stop Method 0 4 8 3 3 5 3 r 3 To work out this sum, divide 353 by 4, one digit at a time, starting from the left. Definitions Short Division Long Division Practice Main Menu

Short Division Repeated Subtraction You can use repeated subtraction. For example: 30 ÷ 6 Subtract 6 30 – 6 = 24 Subtract 6 24 – 6 = 18 Subtract 6 18 – 6 = 12 Subtract 6 12 – 6 = 6 Subtract 6 6– 6 = 0 There is nothing left so no remainder Count the number of subtractions Definitions Short Division Long Division 5 30 ÷ 6 = 5 Practice Main Menu

Short Division Repeated Subtraction Another example: 90 ÷ 17 Short Division 90 – 17 = 73 Subtract 17 73 – 17 = 55 Subtract 17 55 – 17 = 38 Subtract 17 38 – 17 = 21 Subtract 17 21 – 17 = 4 There is 4 left over so this is the remainder Count the number of subtractions Definitions Subtract 17 5 Long Division 90 ÷ 17 = 5 r 4 Practice Main Menu

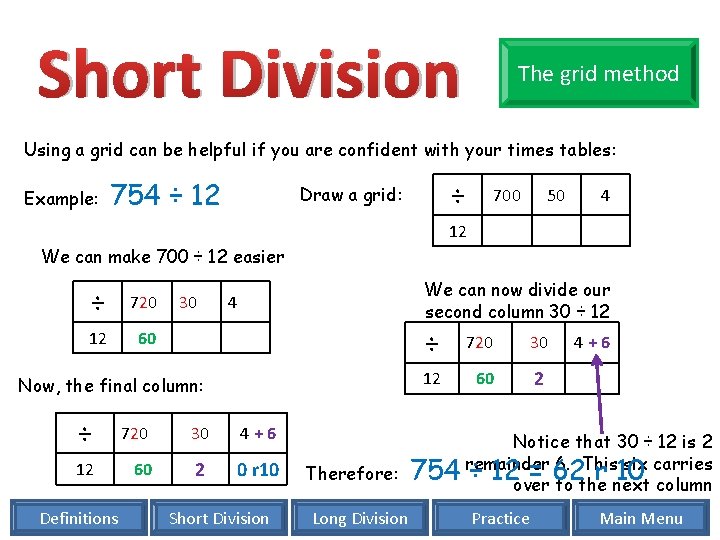
Short Division The grid method Using a grid can be helpful if you are confident with your times tables: Example: 754 ÷ 12 ÷ Draw a grid: 700 50 4 12 We can make 700 ÷ 12 easier ÷ 720 12 60 30 We can now divide our second column 30 ÷ 12 4 Now, the final column: ÷ 720 30 4+6 12 60 2 0 r 10 Definitions Short Division ÷ 720 30 12 60 2 4+6 Notice that 30 ÷ 12 is 2 remainder 6. This six carries Therefore: 754 ÷ 12 = 62 r 10 over to the next column Long Division Practice Main Menu

Short Division Want to practice? NO- I’m ready for long division YES- I want to practice reversing multiplication Reversing multiplication solutions YES- I want to practice the bus stop method Bus stop method solutions YES- I want to practice the grid method Grid method solutions Definitions Long Division Main Menu

Long Division Repeated Subtraction The Traditional Method Definitions Short Division Main Menu

Long Division Repeated Subtraction Lets try: 543 ÷ 16 543 Start with we know 10 x 16 = 160 - 160 We cannot subtract another 160 so look - 32 for a lower multiple - 16 (10 x 16) 383 (10 x 16) 223 (10 x 16) 63 (2 x 16) 31 (1 x 16) 15 15 cannot be divided by 16 so this is the remainder We have used 10 + 2 + 1 lots of 16. This means we divided 33 times 543 ÷ 16 = 33 remainder 15 Definitions Short Division Long Division Practice Main Menu

Long Division Repeated Subtraction Lets try: 1748 ÷ 42 1748 Start with we know 10 x 42 = 420 - 420 We cannot subtract another 420 so look - 42 for a lower multiple (10 x 42) 1328 (10 x 42) 908 (10 x 42) 488 26 cannot be divided 68 (1 x 42) by 42 so this is the 26 remainder We have used 10 + 1 lots of 42. This means we divided 41 times 1748 ÷ 42 = 41 remainder 26 Definitions Short Division Long Division Practice Main Menu

Long Division Lets try: 9265 ÷ 37 9265 Start with we know 100 x 37 = 3700 - 3700 We cannot subtract another 3700 so - 740 look for a lower multiple - 740 We cannot subtract another 740 so look - 370 for a lower multiple Repeated Subtraction (100 x 37) (20 x 37) (10 x 37) 5564 1865 1125 385 15 15 cannot be divided by 37 so this is the remainder We have used 100 + 20 + 10 lots of 37. This means we divided 250 times 9265 ÷ 37 = 250 remainder 15 Definitions Short Division Long Division Practice Main Menu

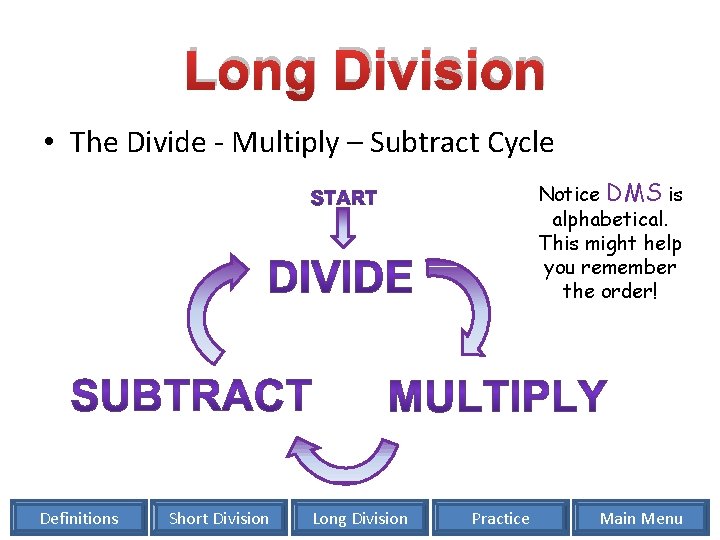
Long Division • The Divide - Multiply – Subtract Cycle Notice DMS is alphabetical. This might help you remember the order! Definitions Short Division Long Division Practice Main Menu

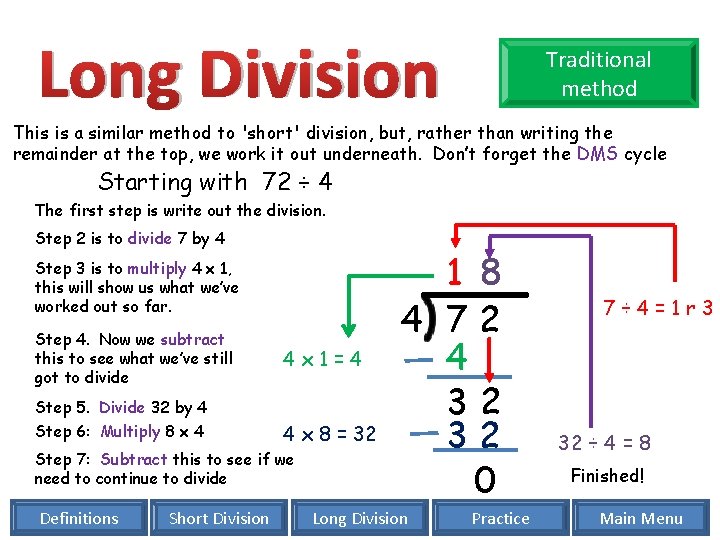
Long Division Traditional method This is a similar method to 'short' division, but, rather than writing the remainder at the top, we work it out underneath. Don’t forget the DMS cycle Starting with 72 ÷ 4 The first step is write out the division. Step 2 is to divide 7 by 4 Step 3 is to multiply 4 x 1, this will show us what we’ve worked out so far. Step 4. Now we subtract this to see what we’ve still got to divide Step 5. Divide 32 by 4 Step 6: Multiply 8 x 4 4 x 1=4 4 x 8 = 32 Step 7: Subtract this to see if we need to continue to divide Definitions Short Division 1 8 4 72 4 32 32 0 Long Division Practice 7÷ 4=1 r 3 32 ÷ 4 = 8 Finished! Main Menu

Long Division Traditional method This is a similar method to 'short' division, but, rather than writing the remainder at the top, we work it out underneath. Let’s try 156 ÷ 4 Definitions 0 4 1 0 1 1 Short Division 3 9 5 6 5 2 3 6 0 Long Division Finished! Practice Main Menu

Long Division Traditional method This is a similar method to 'short' division, but, rather than writing the remainder at the top, we work it out underneath. Let’s try 156 ÷ 4 Definitions 0 5 2 0 2 2 Short Division 5 5 7 5 2 5 0 Long Division Finished! Practice Main Menu

Long Division Traditional method This is a similar method to 'short' division, but, rather than writing the remainder at the top, we work it out underneath. Let’s try 3749 ÷ 12 Definitions 12 Short Division 312 r 5 3749 36 1 4 1 2 29 24 5 Long Division Practice Finished! Main Menu

Long Division Traditional method This is a similar method to 'short' division, but, rather than writing the remainder at the top, we work it out underneath. Let’s try 3749÷ 31 We may find this useful: 31 62 93 124 155 186 217 248 279 310 Definitions 31 Short Division 1 2 0 r 5 3 7 4 9 31 6 4 62 2 9 24 5 Long Division Practice Finished! Main Menu

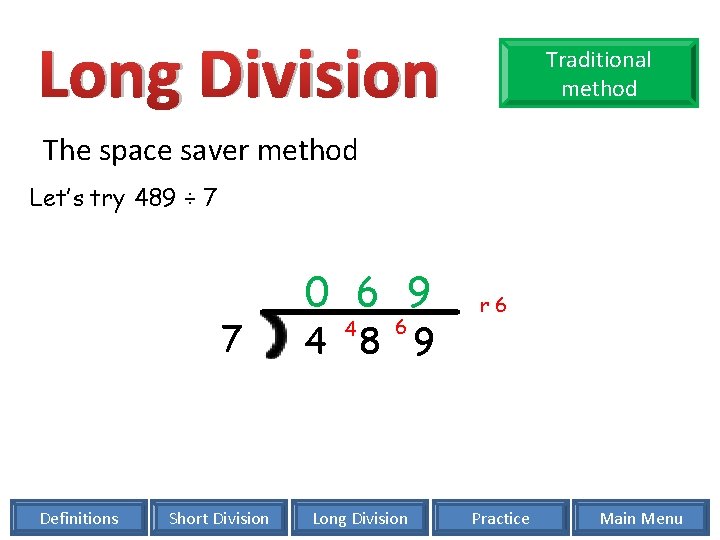
Long Division Traditional method The space saver method Let’s try 489 ÷ 7 7 Definitions Short Division 0 6 9 4 6 4 8 9 Long Division r 6 Practice Main Menu

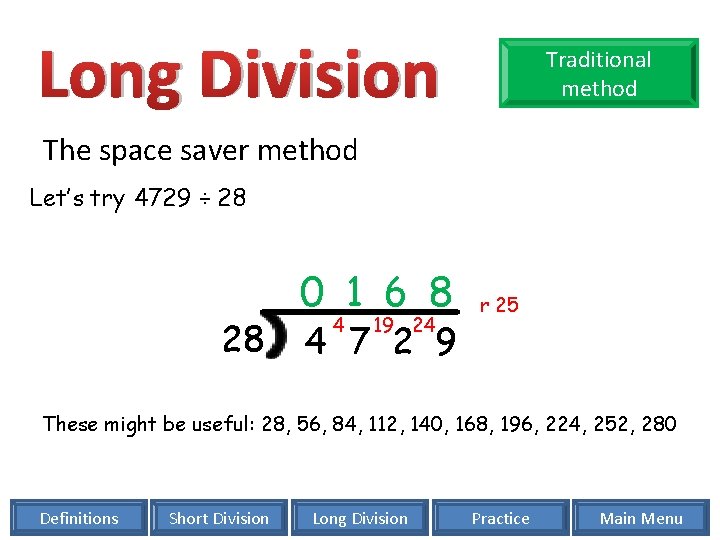
Long Division Traditional method The space saver method Let’s try 4729 ÷ 28 28 0 1 6 8 4 19 24 4 7 2 9 r 25 These might be useful: 28, 56, 84, 112, 140, 168, 196, 224, 252, 280 Definitions Short Division Long Division Practice Main Menu

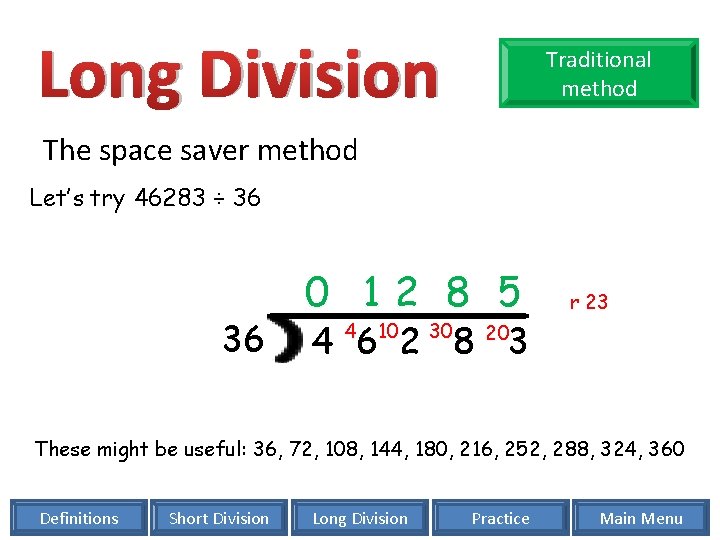
Long Division Traditional method The space saver method Let’s try 46283 ÷ 36 36 0 12 8 5 4 6 2 8 3 4 10 30 r 23 20 These might be useful: 36, 72, 108, 144, 180, 216, 252, 288, 324, 360 Definitions Short Division Long Division Practice Main Menu

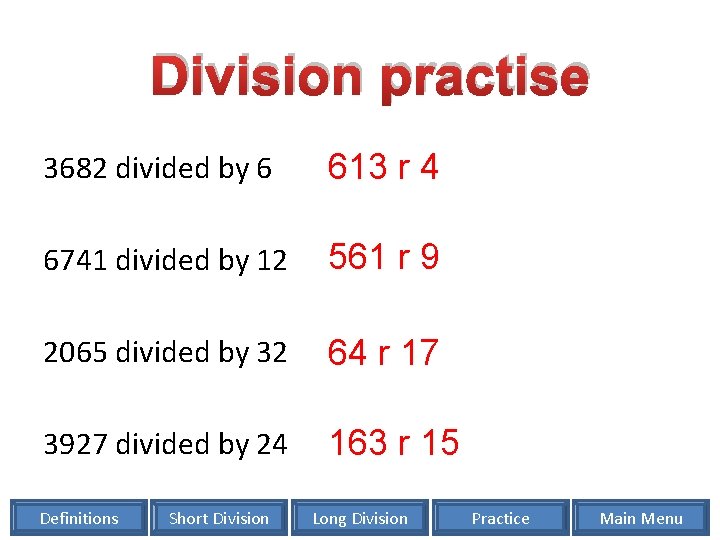
Division practise 3682 divided by 6 613 r 4 6741 divided by 12 561 r 9 2065 divided by 32 64 r 17 3927 divided by 24 163 r 15 Definitions Short Division Long Division Practice Main Menu

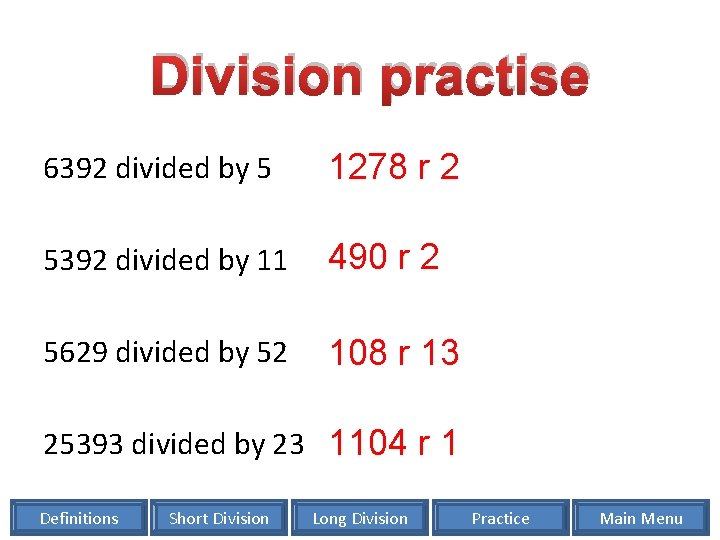
Division practise 6392 divided by 5 1278 r 2 5392 divided by 11 490 r 2 5629 divided by 52 108 r 13 25393 divided by 23 1104 r 1 Definitions Short Division Long Division Practice Main Menu

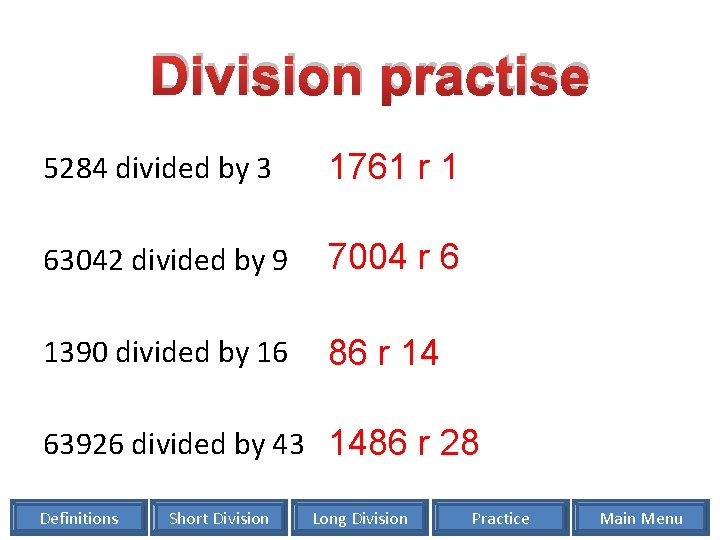
Division practise 5284 divided by 3 1761 r 1 63042 divided by 9 7004 r 6 1390 divided by 16 86 r 14 63926 divided by 43 1486 r 28 Definitions Short Division Long Division Practice Main Menu

Long Division Want to practice more? NO. All finished. YES- I want to practice repeated subtraction Repeated subtraction solutions YES- I want to practice the traditional method Traditional method solutions