Divide Conquer Recurrence Relations 6 3 Divide and

Divide & Conquer Recurrence Relations 6. 3 Divide and Conquer Main points so far: Many types of problems are solvable by reducing a problem of size n into some number a of independent subproblems, each of size n/b , where a 1 and b>1. (많은 경우에 있어서, 크기 n의 문제를 a개의 크기 n/b 의 작은 문제로 바꾸어 처리할 수 있다. ) The time complexity to solve such problems is given by a recurrence relation: T(n) = a·T( n/b ) + g(n) (이런 경우의 시간 복잡도는 T(n)의 점화 관계로 나타낼 수 있다. ) Time to break problem up into sub-problems Time for each sub-problem Page 2 Discrete Mathematics by Yang-Sae Moon

Divide & Conquer Examples 6. 3 Divide and Conquer Binary search: Break list into 1 sub-problem (smaller list) (so a=1) of size n/2 (so b=2). • So T(n) = T( n/2 )+c (g(n)=c constant) Merge sort: Break list of length n into 2 sub-lists (a=2), each of size n/2 (so b=2), then merge them, in g(n) = (n) time. • So T(n) = 2 T( n/2 ) + cn (roughly, for some c) Page 3 Discrete Mathematics by Yang-Sae Moon

Fast Multiplication Example (1/3) 6. 3 Divide and Conquer The ordinary grade-school algorithm takes (n 2) steps to multiply two n-digit numbers. (학교에서 배운 방법에 따르면, n자리인 두 수의 곱은 (n 2) 스텝이 필요하다. ) • This seems like too much work! So, let’s find a faster multiplication algorithm! To find the product cd of two 2 n-digit base-b numbers, c=(c 2 n-1 c 2 n-2…c 0)b and d=(d 2 n-1 d 2 n-2…d 0)b, first, we break c and d in half: c=bn. C 1+C 0, d=bn. D 1+D 0, (e. g. , 4321 = 102 43+21) and then. . . (see next slide) Page 4 Discrete Mathematics by Yang-Sae Moon

Fast Multiplication Example (2/3) 6. 3 Divide and Conquer Zero (Factor last polynomial) Three multiplications, each with n-digit numbers Page 5 Discrete Mathematics by Yang-Sae Moon

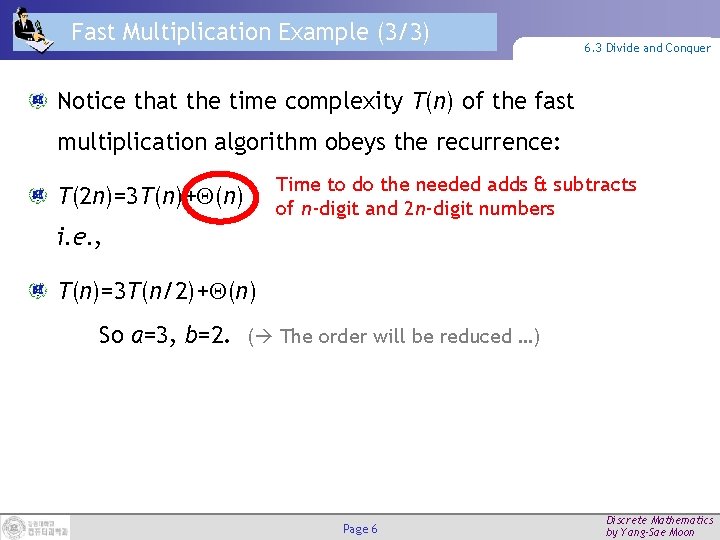
Fast Multiplication Example (3/3) 6. 3 Divide and Conquer Notice that the time complexity T(n) of the fast multiplication algorithm obeys the recurrence: T(2 n)=3 T(n)+ (n) Time to do the needed adds & subtracts of n-digit and 2 n-digit numbers i. e. , T(n)=3 T(n/2)+ (n) So a=3, b=2. ( The order will be reduced …) Page 6 Discrete Mathematics by Yang-Sae Moon

The Master Theorem 6. 3 Divide and Conquer Consider a function f(n) that, for all n=bk for all k Z+, satisfies the recurrence relation: (n=bk 일 때, 다음 점화 관계가 성립하면) f(n) = af(n/b) + cnd with a≥ 1, integer b>1, real c>0, d≥ 0. Then: Proof of theorem is …. omitted. Page 7 Discrete Mathematics by Yang-Sae Moon

Master Theorem Examples (1/3) 6. 3 Divide and Conquer Recall that complexity of fast multiplication was: T(n)=3 T(n/2)+ (n) Thus, a=3, b=2, d=1. So a > bd, so case 3 of the master theorem applies, so: which is O(n 1. 58…), so the new algorithm is strictly faster than ordinary (n 2) multiply! Page 8 Discrete Mathematics by Yang-Sae Moon