Disjunctive Normal Form CS 270 Math Foundations of

Disjunctive Normal Form CS 270: Math Foundations of CS Jeremy Johnson

Boolean Expressions A Boolean expression is a Boolean function Any Boolean function can be written as a Boolean expression s x 0 x 1 f 0 0 Disjunctive normal form (sums of products) For each row in the truth table where the output is true, write a product such that the corresponding input is the only input combination that is true Not unique E. G. (multiplexor function) 0 0 1 0 0 1 1 0 0 0 1 1 0 0 1 1 2

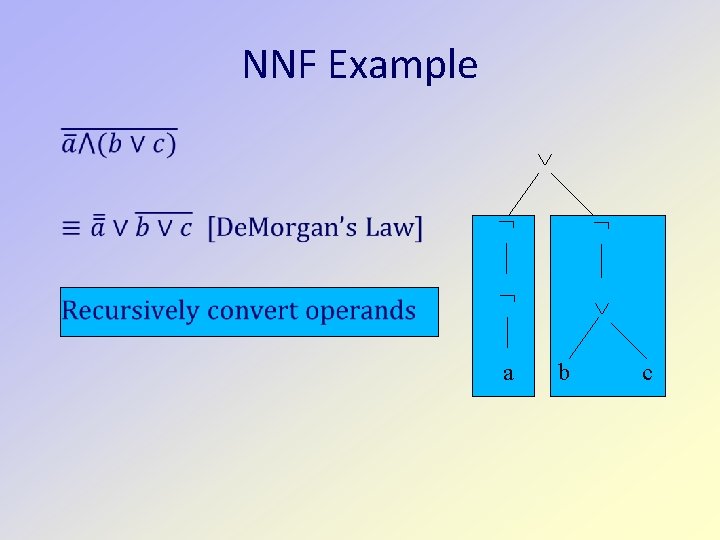
Disjunctive Normal Form Theorem. Any boolean expression can be converted to an equivalent boolean exprssion in DNF. Proof. Any boolean expression defines a boolean function. Construct the truth table for the boolean expression and use the procedure on the previous slide to construct a boolean expression in DNF for the function defined by the truth table.

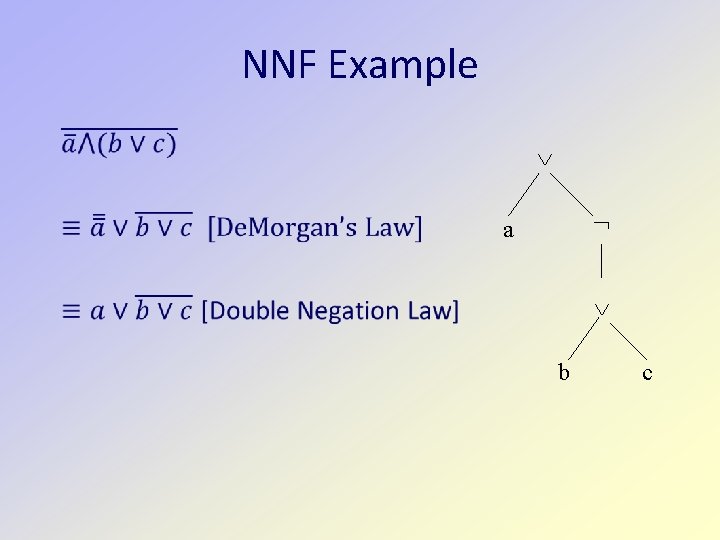
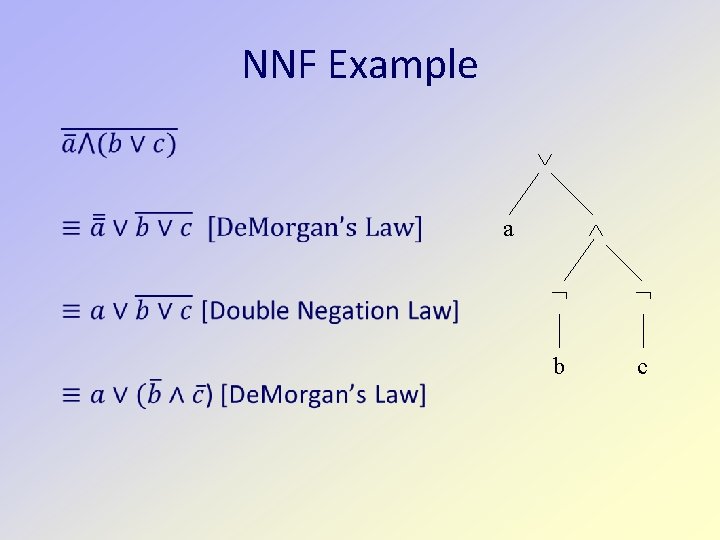
Alternative Proof A recursive conversion algorithm with corresponding inductive proof of correctness. Assume that implications and equivalences have been removed Assume that constants have been eliminated First convert to Negative Normal Form (NNF) (not expr) only occurs when expr is a variable Use De. Morgan’s Law and Double Negation Law Then convert to DNF Distribute and over or

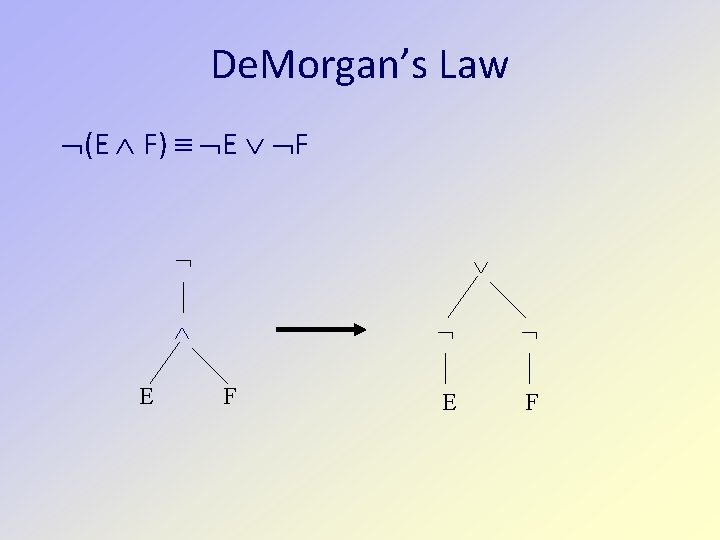
De. Morgan’s Law (E F) E F E F

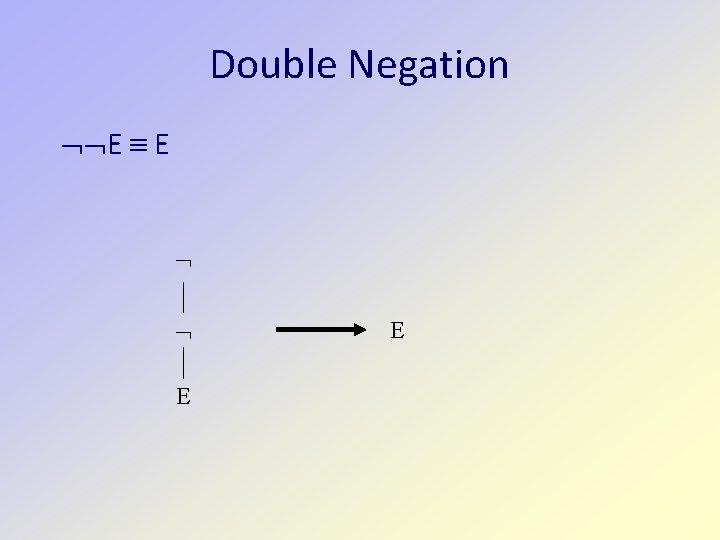
Double Negation E E E E

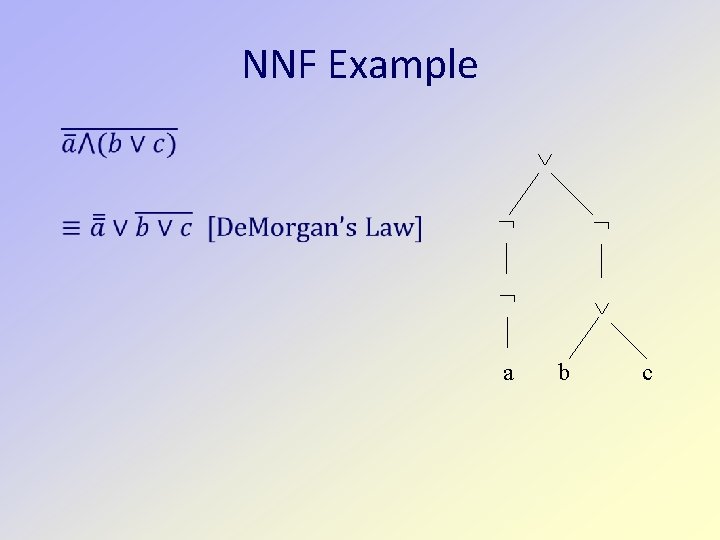
NNF Example a b c

NNF Example a b c

NNF Example a b c

NNF Example a b c

NNF Example a b c

Is-NNF ; Input: a boolean expression ; Output: a boolean which is true if the input expression is in negative normal ; form. (define (is-nnf? expr) (cond [ (is-constant? expr) #t ] [ (is-variable? expr) #t ] [ (is-not? expr) (is-variable? (op 1 expr)) ] [ (is-or? expr) (and (is-nnf? (op 1 expr)) (is-nnf? (op 2 expr))) ] [ (is-and? expr) (and (is-nnf? (op 1 expr)) (is-nnf? (op 2 expr))) ] ) )

NNF ; Input: A boolean expression ; Output: A boolean expression that is equivalent to the input and ; is in negative normal form. ; (and (is-nnf? (nnf expr)) (equal? (bool-eval expr env)) ; (equal? (bool-eval (nnf expr) env))) (define (nnf expr) (cond [ (is-constant? expr) expr ] [ (is-variable? expr) expr ] [ (is-not? expr) (nnf-not expr) ] [ (is-or? expr) (list 'or (nnf (op 1 expr)) (nnf (op 2 expr))) ] [ (is-and? expr) (list 'and (nnf (op 1 expr)) (nnf (op 2 expr))) ] ) )

NNF ; Input: A boolean expression that is a negation. ; Output: A boolean expression that is in NNF and equivalent to the input. (define (nnf-not expr) (cond [ (is-constant? (op 1 expr)) (not expr) ] [ (is-variable? (op 1 expr)) expr ] [ (is-not? (op 1 expr)) (nnf (op 1 expr))) ] [ (is-or? (op 1 expr)) (list 'and (nnf (list 'not (op 1 expr)))) (nnf (list 'not (op 2 (op 1 expr))))) ] [ (is-and? (op 1 expr)) (list 'or (nnf (list 'not (op 1 expr)))) (nnf (list 'not (op 2 (op 1 expr))))) ] ) )

Correctness (is-nnf? (nnf expr) (bool-eval (nnf expr) env) = (bool-eval expr env) Structural induction on expr using De Morgan’s laws and Double Negation law (not (and p q)) (or (not p) (not q)) (not (or p q)) (and (not p) (not q)) (not p)) p Base case. expr = var or (not var) Assume true for expr 1 and expr 2 and show for (not expr), (or expr 1 expr 2), and (and expr 1 expr 2) – and or are trivial

Correctness for (not expr) (is-nnf? (nnf ‘(not expr)) = (nnf-not ‘(not expr)) Case 1. (nnf-not ‘(not expr))) = (nnf expr)) which is correct by induction and double negation Case 2. (nnf-not ‘(not (and expr 1 expr 2))) = (nnf ‘(or (not expr 1) (not expr 2))) = (list ‘or (nnf ‘(not expr 1)) (nnf ‘(not expr 2))) which is correct by induction and De Morgan Case 3. (nnf-not ‘(not (or expr 1 expr 2)))

Is-DNF (defun is-dnf (expr) (and (is-nnf expr) (no-andor expr)) ) ; no and above or (defun no-andor (expr) (cond ( (is-constant expr) t ) ( (is-variable expr) t ) ( (is-not expr) (no-andor (op 1 expr)) ) ( (is-or expr) (and (no-andor (op 1 expr)) (no-andor (op 2 expr))) ) ( (is-and expr) (and (no-or (op 1 expr)) (no-or (op 2 expr))) )

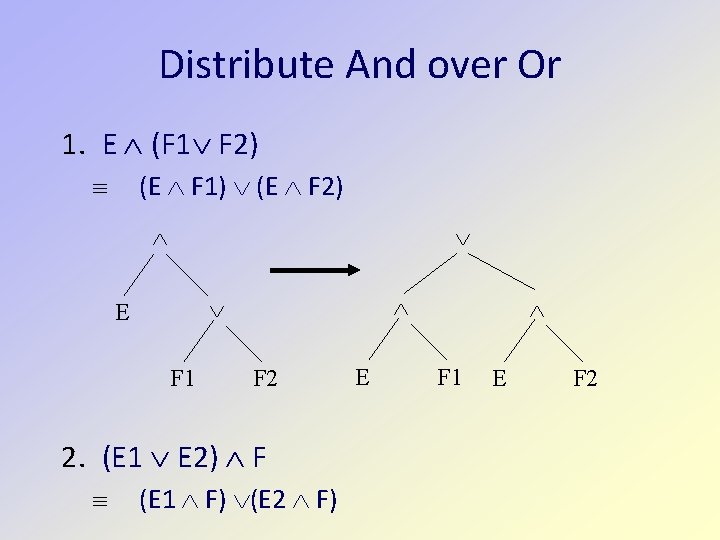
Distribute And over Or 1. E (F 1 F 2) (E F 1) (E F 2) E F 1 F 2 2. (E 1 E 2) F (E 1 F) (E 2 F) E F 1 E F 2

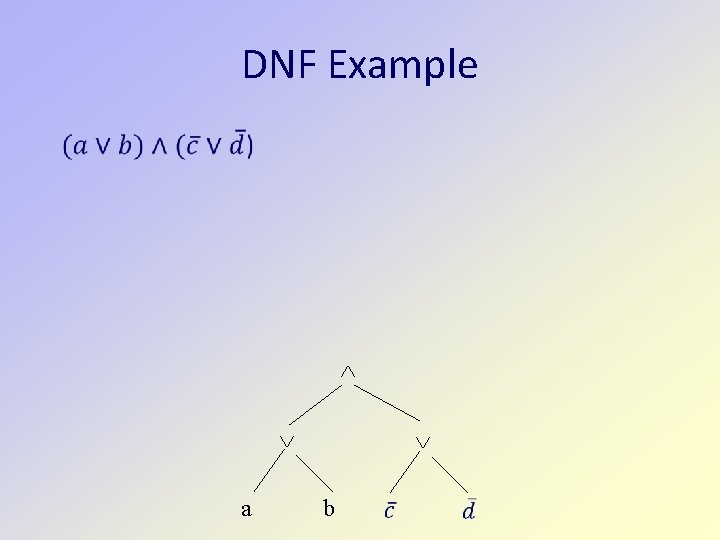
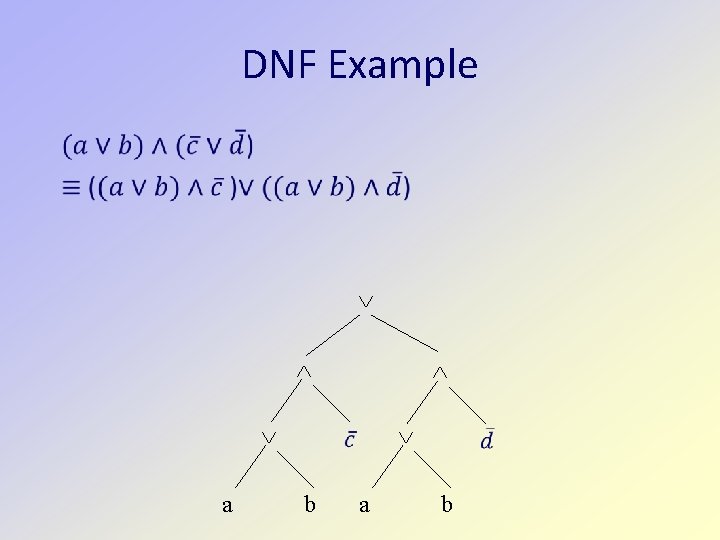
DNF Example a b

DNF Example a b a b

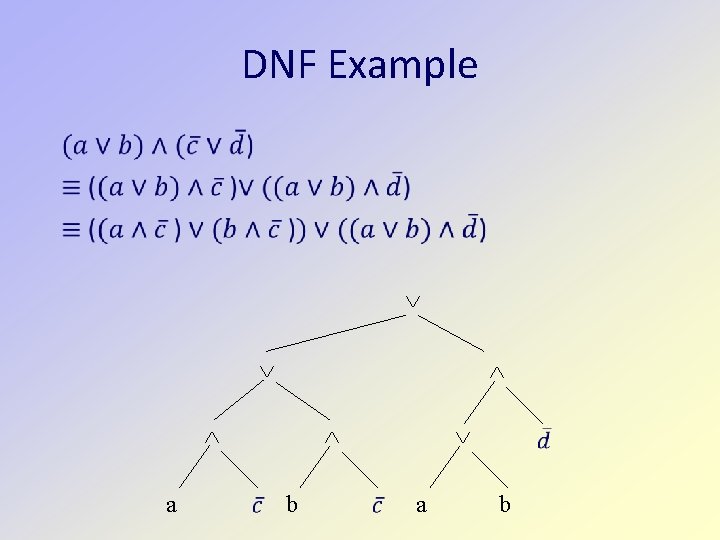
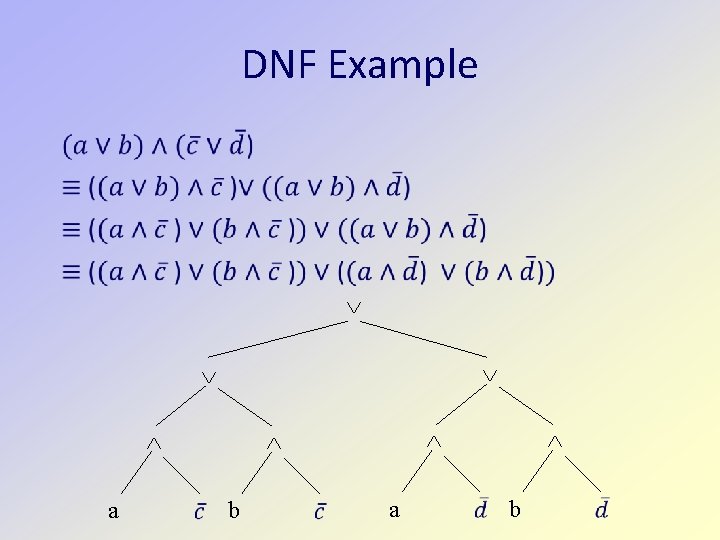
DNF Example a b

DNF Example a b a b

Is-DNF ; is-dnf? Check to see if a Boolean expression is in DNF. This is true when it ; is in NNF and there are no ands above ors. (define (is-dnf? expr) (and (is-nnf? expr) (no-and-above-or? expr)) ; no-and-above-or? Check to see (define (no-and-above-or? expr) (cond [ (is-constant? expr) #t ] [ (is-variable? expr) #t ] [ (is-not? expr) (no-and-above-or? (op 1 expr)) ] [ (is-or? expr) (and (no-and-above-or? (op 1 expr)) (no-and-above-or? (op 2 expr))) ] [ (is-and? expr) (and (no-or? (op 1 expr)) (no-or? (op 2 expr))) ] ) )

Is-DNF ; no-or? check if a boolean expression contains any ors. (define (no-or? expr) (cond [ (is-constant? expr) #t ] [ (is-variable? expr) #t ] [ (is-not? expr) (no-or? (op 1 expr)) ] [ (is-or? expr) #f ] [ (is-and? expr) (and (no-or? (op 1 expr)) (no-or? (op 2 expr))) ] ) )

DNF ; Input: A boolean expression ; Output: A boolean expression in DNF that is equivalent to the input expression. (define (dnf expr) (nnf 2 dnf (nnf expr))) ; Input: A boolean expression in NNF ; Output: A boolean expression in DNF that is equivalent to the input expression. (define (nnf 2 dnf expr) (cond [ (is-constant? expr) expr ] [ (is-variable? expr) expr ] [ (is-not? expr) expr ] [ (is-and? expr) (distrib-andor (dnf (op 1 expr)) (dnf (op 2 expr))) ] [ (is-or? expr) (list 'or (dnf (op 1 expr)) (dnf (op 2 expr))) ] ) )

Distribute And Over Or 1. (and E (or F 1 F 2)) (or (and E F 1) (and E F 2)) 2. (and (or E 1 E 2) F) (or (and E 1 F) (and E 2 F)) 3. (and (or E 1 E 2) (or (F 1 F 2)) (or (and E 1 F 1) (and E 1 F 2) (and E 2 F 1) (and E 2 F 2)) (or (and E 1 F 1) (or (and E 1 F 2) (or (and E 2 F 1) (and E 2 F 2))))

Distribute And Over Or ; Input: Two expressions in DNF ; Output: An expression in DNF equivalent to (and expr 1 expr 2) ; There are three cases. Let expr 1 = E 1 and expr 2 = E 2 ; 1) E 1 = E 11 / E 12. (E 11 / E 2) / (E 12 / E 2) ; 2) E 2 = E 21 / E 22. (E 1 / E 21) / (E 1 / E 22) ; 3) E 1 and E 2 contain no ors. E 1 / E 2 (define (distrib-andor expr 1 expr 2) (cond [(is-or? expr 1) (list 'or (distrib-andor (op 1 expr 1) expr 2) (distrib-andor (op 2 expr 1) expr 2)) ] [(is-or? expr 2) (list 'or (distrib-andor expr 1 (op 1 expr 2)) (distrib-andor expr 1 (op 2 expr 2))) ] [ else (list 'and expr 1 expr 2) ] ) )

Exponential Blowup Converting the following expression shows that an exponential increase in the size of the dnf from of a boolean expression is possible (x 1 y 1) (xn yn) (x 1 xn) (y 1 yn)

Exercise Prove that (dnf expr) terminates Hint show that the size of expr decreases in all recursive calls and that the base case must eventually be reached, where size of an expr is the number of not, and or operations. Use induction to prove (is-dnf (dnf expr)) Modify (dnf expr) to compute the conjunctive normal form (cnf expr). Hint cnf is duel to dnf

Proof of Correctness of dnf Must show the following (bool-eval (dnf expr) env) = (bool-eval expr env) (is-dnf? (dnf expr)) We first prove the following lemmas Lemma 1. (implies (and (is-dnf expr 1) (is-dnf? expr 2)) (is-dnf? (list ‘or expr 1 expr 2))) Lemma 2. (implies (and (is-dnf? expr 1) (is-dnf? expr 2)) (is-dnf? (distrib-andor expr 1 expr 2))) Lemma 3. (bool-eval (list ‘and expr 1 expr 2) env) = (bool-eval (distrib-andor exp 1 exp 2) env)

Proof of Lemma 1 (is-dnf (list ‘or expr 1 expr 2)) = (and (is-nnf? (list ‘or expr 1 expr 2)) (no-and-above-or? (list ‘or expr 1 expr 2))) {def} (is-nnf? (list ‘or expr 1 expr 2)) = (and (is-nnf? expr 1) (is-nnf? expr 2)) {def} = (and t t) {assumption}

Proof of Lemma 1 (no-and-above-or? (list ‘or expr 1 expr 2)) = (and (no-and-above-or? expr 1) (no-andabove-or? expr 2)) {def} = (and t t) {assumption}

Proof of Lemma 2 (is-dnf? (distrib-andor expr 1 expr 2) The proof is by induction on boolean expressions. There are three cases to consider 1. (is-or? expr 1) 2. (is-or? expr 2) 3. (and (not (is-or? expr 1)) (not (is-or? expr 2))) In case 3, the base case, we return (and expr 1 expr 2), and since expr 1 and expr 2 are in dnf, and are conjunctions, there are no or’s in expr 1 and expr 2 and consequently (no-andabove-or? (and expr 1 expr 2)). Similarly (is-nnf? (and expr 1 expr 2)) is true, thus (is-dnf? (and expr 1 expr 2)) The proofs for cases 1 and 2 are similar for both cases. We do case 1.

Proof of Lemma 2 (is-dnf? (distrib-andor expr 1 expr 2) = (is-dnf (list 'or (distrib-andor (op 1 expr 1) expr 2) (distribandor (op 2 expr 1) expr 2)) ) Since (is-dnf? expr 1), (is-dnf? (op 1 expr)) and (is-dnf? (op 2 expr)). Therefore we can apply the induction hypothesis and conclude that (is-dnf? (distrib-andor (op 1 expr 1) expr 2) and (is-dnf? (distrib-andor (op 2 expr 1) expr 2). Thus, by Lemma 1, the lemma is proved.

Proof of Lemma 3 follows by induction on boolean expressions and uses the distributive property of boolean algebra to prove the result after applying the inductive hypothesis.

Proof of Correctness To show (is-dnf? (dnf expr)) = (is-dnf? (nnf 2 dnf (nnf expr))) we already showed (is-nnf? (nnf expr)) so we assume that expr is in NNF and show (is-dnf? (nnf 2 dnf expr)) 1) [base cases] expr = var, expr = const, expr = (not var) In all cases (nn 2 dnf expr) = expr and (is-dnf? expr) is true.

Proof of Correctness 2) [(is-or? expr)] (nn 2 dnf expr) = (list 'or (nnf 2 dnf (op 1 expr)) (nnf 2 dnf (op 2 expr))) By induction (is-dnf? (nnf 2 dnf (op 1 expr)) ) and (is-dnf? (nnf 2 dnf (op 2 expr)) ). Therefore by Lemma 1, (is-dnf? (list 'or (nnf 2 dnf (op 1 expr)) (nnf 2 dnf (op 2 expr))))

Proof of Correctness 3) [(is-and? expr)] (nn 2 dnf expr) = (distrib-andor (nnf 2 dnf (op 1 expr)) (nnf 2 dnf (op 2 expr))) By induction (is-dnf? (nnf 2 dnf (op 1 expr)) ) and (is-dnf? (nnf 2 dnf (op 2 expr)) ). Therefore by Lemma 2, (is-dnf? (distrib-andor (nnf 2 dnf (op 1 expr)) (nnf 2 dnf (op 2 expr))))

Proof of Correctness To show (bool-eval (dnf expr) env) = (bool-eval (nnf 2 dnf (nnf expr)) env) = (bool-eval expr env) we again, having shown (bool-eval (nnf expr) env) = (bool-eval expr env), assume (is-nnf expr) and show (bool-eval (nnf 2 dnf expr) env) = (bool-eval expr env) Just as in the previous proof, we use induction on boolean expressions. The base cases are trivial and the recursive case for or is immediate after applying induction. The recursive case for and requires Lemma 3.