Discrete Math II Introduction Howon Kim 2019 9

Discrete Math II - Introduction - Howon Kim 2019. 9. 2

About this course… n Course name : Discrete Math II (CP 21697) § - - Study the basics on number theory, graph theory, automata, and mathematical techniques for computer science & engineering Number theory (finite fields and ring) is the fundamental knowledge for the cryptography & security and Coding Theory etc. Graph theory & automata is the basic mathematical techniques to understand the computer science, networks and many topics in computer engineering 2

About this course… n About Instructor - n Office : A 06 -503 Office hours : 12: 30 ~ 13: 30 PM(Monday, Wednesday) Email: howonkim@gmail. com, howonkim@pusan. ac. kr Phone: 010 -8540 -6336 Homepage : http: //infosec. pusan. ac. kr Major Research Interests § § § § 지능형 사물인터넷(Intelligent Io. T) 연구 블록체인(Blockchain) 연구 딥러닝, 산업용 AI 연구 암호(Cryptography), 정보보호(Information Security), Io. T 보안 암호 칩, 보안 칩 설계 연구, TLS 전용 칩 개발 국가보안기술연구소, ETRI, KISA와 공동연구 부산대학교 사물인터넷 연구센터, 블록체인 전문연구실 운영 중 3

About this course… n Textbook - - n Time & Classroom - n “Discrete and combinatorial mathematics ” (5 th Ed), R. P. Grimaldi, 2004 Selected Materials for mathematical techniques 13: 30 ~ 14: 45 PM (Monday, Wednesday), A 6 -514호 References - - Discrete mathematics by Richard Johnsonbaugh Introduction to Automata Theory, Languages, and Computation by John E. Hopcroft Introduction to Graph Theory by Douglas B West A Course in Number Theory and Cryptography by Neal Koblitz 4

About this course… n Course Materials http: //infosec. pusan. ac. kr 5

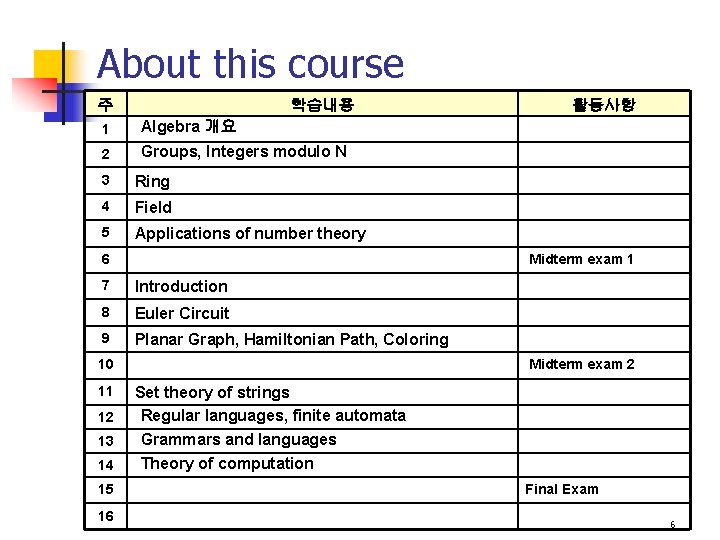
About this course 주 학습내용 1 Algebra 개요 2 Groups, Integers modulo N 3 Ring 4 Field 5 Applications of number theory 6 Midterm exam 1 7 Introduction 8 Euler Circuit 9 Planar Graph, Hamiltonian Path, Coloring 10 11 12 13 14 15 16 활동사항 Midterm exam 2 Set theory of strings Regular languages, finite automata Grammars and languages Theory of computation Final Exam 6

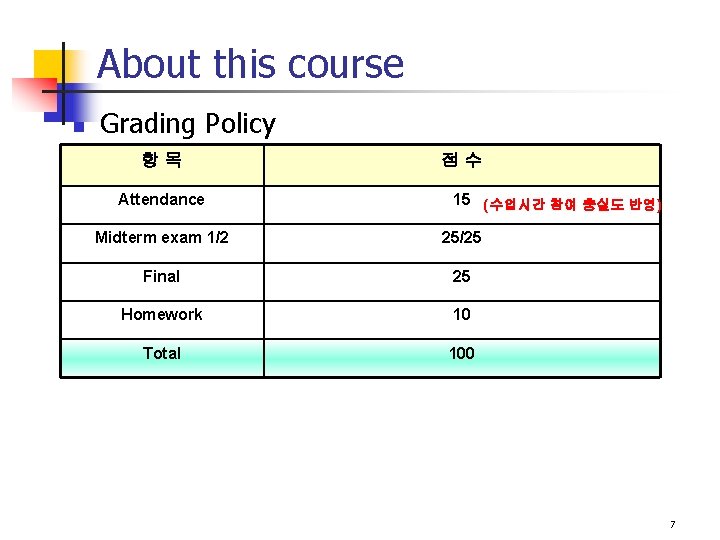
About this course n Grading Policy 항목 Attendance 점수 15 (수업시간 참여 충실도 반영) Midterm exam 1/2 25/25 Final 25 Homework 10 Total 100 7

Algebra n Definition q Tuple <K, op 1, op 2, …, opn> n n n K : a set of data q q n < R, , > < {T, F }, , , > ; Boolean algebra |K| : order finite or infinite Operator opj q Closure opj : Ki K n Unary if i=1, Binary if i=2, … 8

Identity and Zero n : K K K Identity element e for in K (항등원) n e a = a e = a for all a ∈ K Zero element z for in K (영원) n z a = a z = z for all a ∈ K Examples < Z, + > n Identity : 0, Zero : none < Z, > n Identity : 1, Zero : 0 9

Inverse n : K K K Let e be the identity element for in K. q Left inverse n q Right inverse n q a’L a = e , a ∈ K a a’R = e , a ∈ K If a’L = a’R = a’ , a’ is the inverse of a. Example < Z, + > n n Identity 0, (-x) is the inverse of x : x + (-x) = (-x) + x = 0 10

Properties of Operator Let : K K K be a binary operator. (1) Closure (2) Associative (a b) c = a (b c) for all a, b, c ∈ K. (3) Identity There is an identity element e ∈ K for . (4) Inverse For each a ∈ K, there is an inverse a’ ∈ K for . (5) Commutative a b = b a for all a, b ∈K. 11

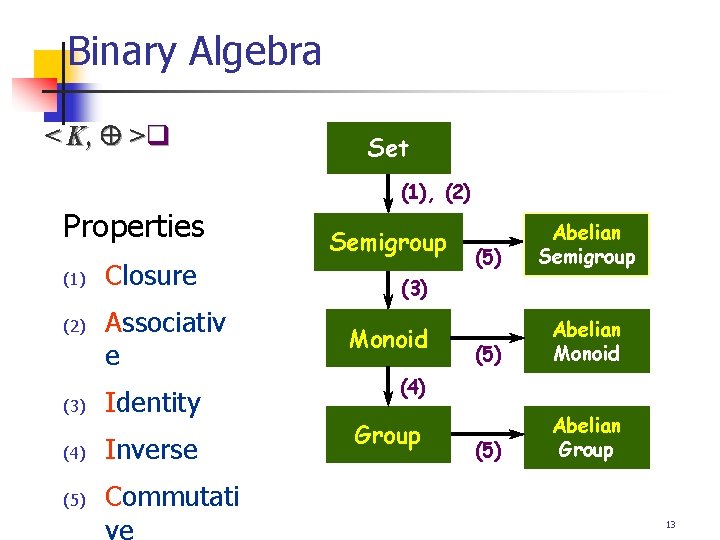
Binary Algebra < K, > for binary operator : K K K 1. Semigroup (반군) : Associative n n 2. n < N, + >, < Z, >, < {T, F }, > A monoid is a set that is closed under an associative binary operation and has an identity element Group (군) : Associative, Identity, Inverse n 4. A semigroup is a set with an associative binary operation which satisfies closure and associative law. Monoid (단위반군) : Associative, Identity n 3. < Z+, + > < Z, + > Abelian group (대수군) : n Associative, Identity, Inverse, Commutative < Z, + > 12

Binary Algebra < K, > q Set (1), (2) Properties (1) (2) (3) (4) (5) Closure Associativ e Identity Inverse Commutati ve Semigroup (5) Abelian Monoid (5) Abelian Group (3) Monoid (4) Group 13

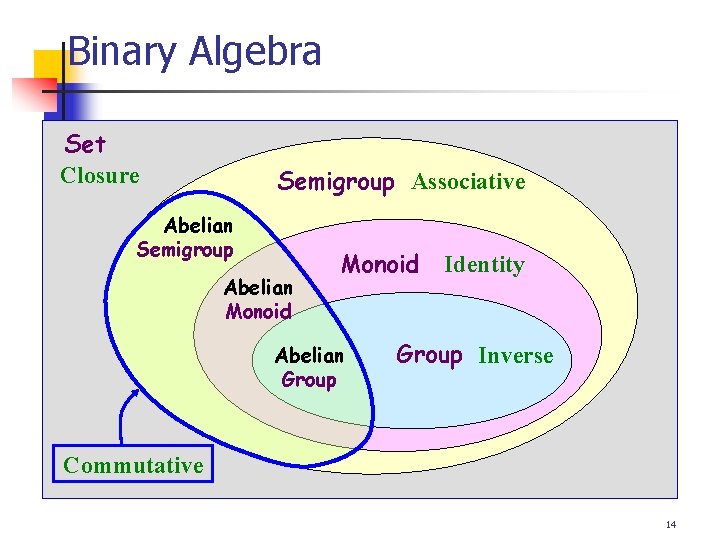
Binary Algebra Set Closure Semigroup Associative Abelian Semigroup Abelian Monoid Abelian Group Identity Group Inverse Commutative 14

Ring ( Two operators ) n < K, , > Two binary operators , : K K K n Conditions for Ring q q q < K, > is an abelian group. is associative is distributive over n n a (b c) = (a b) (a c) and (a b) c = ( a c) ( b c) for all a, b, c ∈ K. 15

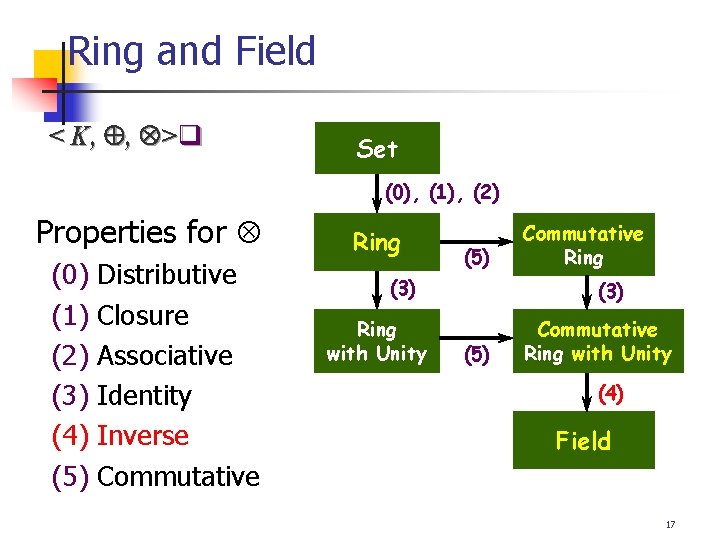
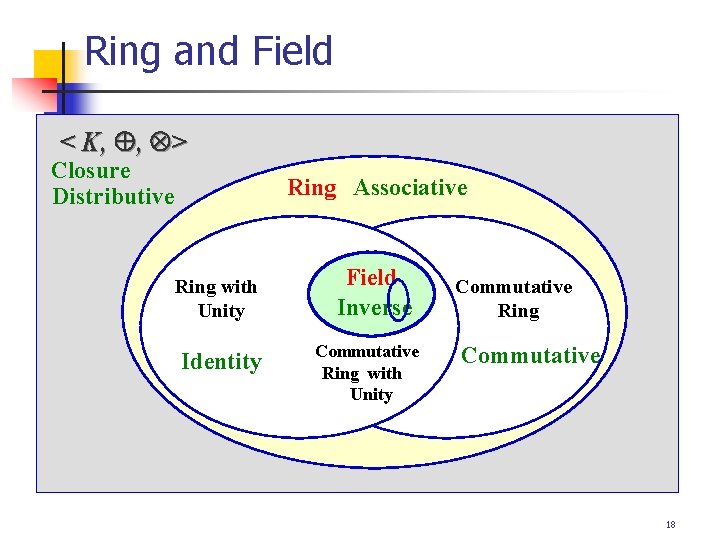
Definitions < K, , > < K, > : abelian group, and distribution laws hold n Conditions for operator : 1. Ring (환) : Associative 2. Ring with Unity : Associative, Identity 3. Commutative Ring : Associative, Commutative 4. Commutative Ring with Unity Associative, Identity, Commutative 5. Field (체) Associative, Identity, Commutative, Inverse 16

Ring and Field < K, , > q Set (0), (1), (2) Properties for (0) (1) (2) (3) (4) (5) Distributive Closure Associative Identity Inverse Commutative Ring (5) (3) Ring with Unity Commutative Ring (3) (5) Commutative Ring with Unity (4) Field 17

Ring and Field < K, , > Closure Distributive Ring Associative Ring with Unity Identity Field Inverse Commutative Ring with Unity Commutative Ring Commutative 18

Next… n Basics on Number Theory… 19

Q&A 20