CS 211 Lecture 21 Graphs shortest path algorithm



![Adjacency matrix: representation of a digraph Use a boolean array b[0. . |V|-1][0. . Adjacency matrix: representation of a digraph Use a boolean array b[0. . |V|-1][0. .](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-9.jpg)
![Adjacency list: representation of a Use array b[0. . |V|– 1] of linked lists Adjacency list: representation of a Use array b[0. . |V|– 1] of linked lists](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-10.jpg)
![Find shortest paths from v to all nodes Initially, L[v] = 0 L[w] = Find shortest paths from v to all nodes Initially, L[v] = 0 L[w] =](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-13.jpg)
![Find shortest paths from v to all nodes Initially, L[v] = 0 // shortest Find shortest paths from v to all nodes Initially, L[v] = 0 // shortest](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-14.jpg)
![Find shortest paths from v to all nodes Initially, L[v] = 0 // shortest Find shortest paths from v to all nodes Initially, L[v] = 0 // shortest](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-15.jpg)
![L[w]= ∞ for all nodes w; L[v]= 0; F= {v}; while (F not empty) L[w]= ∞ for all nodes w; L[v]= 0; F= {v}; while (F not empty)](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-17.jpg)
![L[w]= ∞ for all nodes w; How much time? L[v]= 0; F= {v}; while L[w]= ∞ for all nodes w; How much time? L[v]= 0; F= {v}; while](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-18.jpg)
![L[w]= ∞ for all nodes w; L[v]= 0; F= {v}; while (F not empty) L[w]= ∞ for all nodes w; L[v]= 0; F= {v}; while (F not empty)](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-19.jpg)

![public class Adjacency. List { private LNode[] V; // The adjacency list for the public class Adjacency. List { private LNode[] V; // The adjacency list for the](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-21.jpg)

![while (Fsize != 0) { int f= F[0]; Fsize= remove. Min. Heap(F, Fsize); Iterator while (Fsize != 0) { int f= F[0]; Fsize= remove. Min. Heap(F, Fsize); Iterator](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-23.jpg)
- Slides: 23

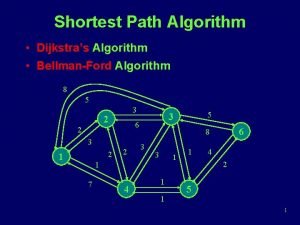
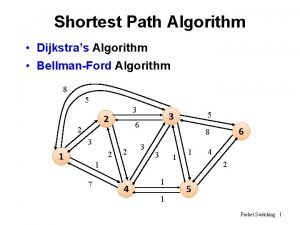
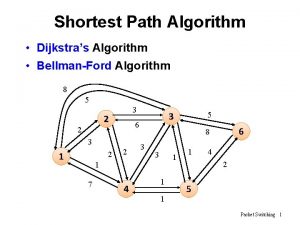
CS 211, Lecture 21 Graphs shortest path algorithm Readings: Weiss, secs. 14. 1 --14. 3, sec. 14. 5. 1. "This 'telephone' has too many shortcomings to be seriously considered as a means of communications. " - Western Union internal memo - 1876 "I think there is a world market for maybe five computers. " - Watson, chair of IBM - 1943 "The problem with television is that the people must sit and keep their eyes glued on a screen; the average American family hasn't time for it. ” - The New York Times - 1949 "Where. . . the ENIAC is equipped with 18, 000 vacuum tubes and weighs 30 tons, computers in the future may have only 1, 000 vacuum tubes and weigh only 1. 5 tons. ” - Popular Mechanics - 1949 "There is no reason anyone would want a computer in their home. " - Ken Olson, founder DEC 1977 "640 K ought to be enough for anybody. ” - Bill Gates - 1981 did he mean memory or money? "By the turn of this century, we will live in a paperless society. " - Roger Smith, chair GM - 1986 "I predict the Internet. . . will go spectacularly supernova and in 1996 catastrophically collapse. " - Bob Metcalfe, inventor and 3 Com founder - 1995 1

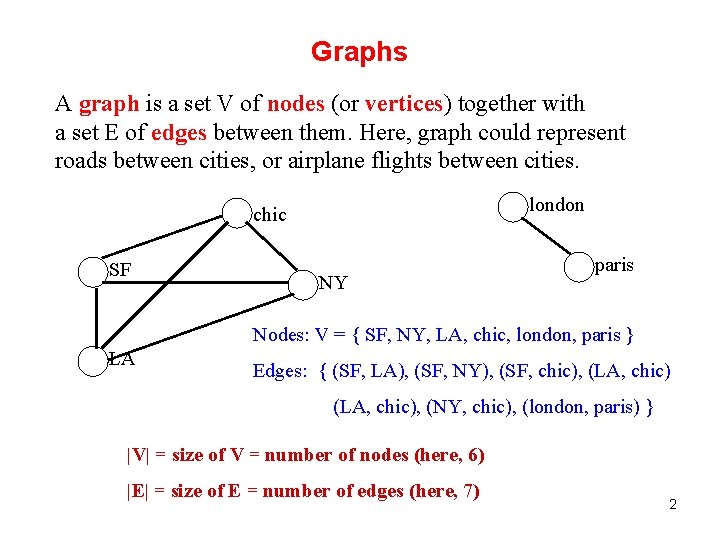
Graphs A graph is a set V of nodes (or vertices) together with a set E of edges between them. Here, graph could represent roads between cities, or airplane flights between cities. london chic SF NY paris Nodes: V = { SF, NY, LA, chic, london, paris } LA Edges: { (SF, LA), (SF, NY), (SF, chic), (LA, chic), (NY, chic), (london, paris) } |V| = size of V = number of nodes (here, 6) |E| = size of E = number of edges (here, 7) 2

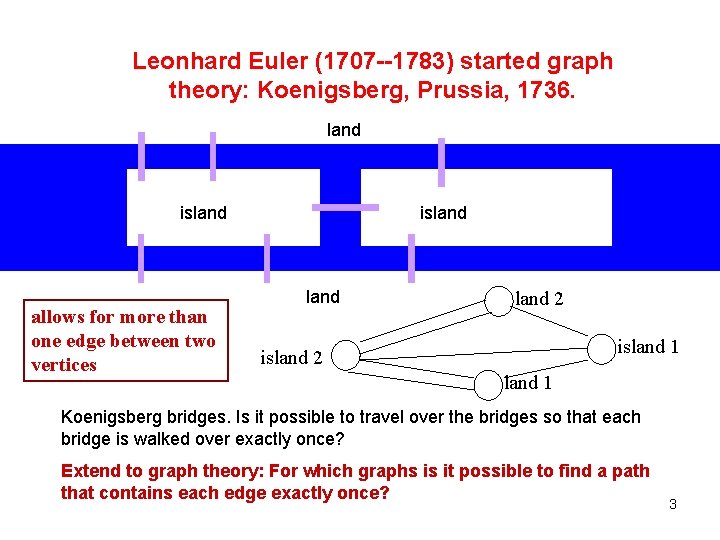
Leonhard Euler (1707 --1783) started graph theory: Koenigsberg, Prussia, 1736. land island allows for more than one edge between two vertices island 2 island 1 island 2 land 1 Koenigsberg bridges. Is it possible to travel over the bridges so that each bridge is walked over exactly once? Extend to graph theory: For which graphs is it possible to find a path that contains each edge exactly once? 3

Important graph problems Traveling salesman problem (TSP): Graph is a bunch of cities, edges have weights that give the cost for traveling from one city to another. Find the cheapest way to travel to all cities and end up back at the home city. Four-color problem. Can one color countries of a map using four colors so that no two adjacent countries have the same color? Nodes: countries. Edges: edge from one country to another if they have a common boundary. Graph is planar --can draw so that no two edges intersect. Color nodes of a graph using four color so that no two adjacent nodes have the same color? About 1870. An incorrect proof published; error detected ~10 years later. 1977: Appel and Haken used computers to solve it (yes, one can). 4

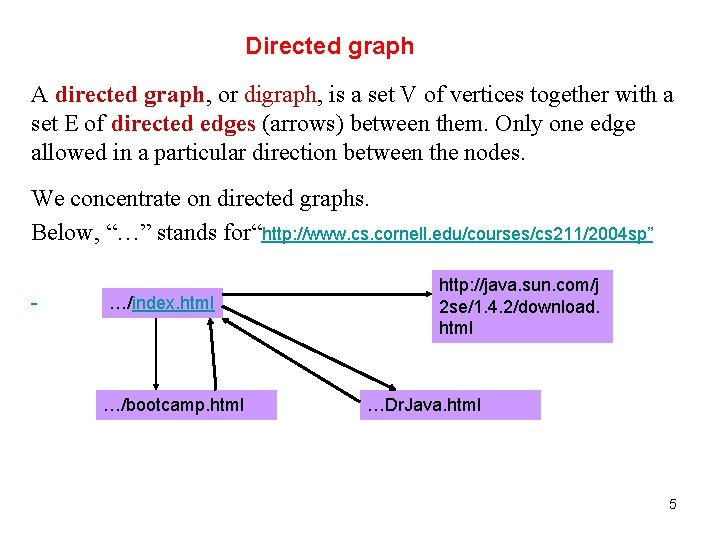
Directed graph A directed graph, or digraph, is a set V of vertices together with a set E of directed edges (arrows) between them. Only one edge allowed in a particular direction between the nodes. We concentrate on directed graphs. Below, “…” stands for“http: //www. cs. cornell. edu/courses/cs 211/2004 sp” …/index. html …/bootcamp. html http: //java. sun. com/j 2 se/1. 4. 2/download. html …Dr. Java. html 5

Celebrity problem uses a directed graph At a party, a celebrity is a person who everyone knows and who knows no one (except themselves). How much time does it take to find a celebrity (if present)? Graph: nodes are people, Edge (p 1, p 2) if p 1 knows p 2. It’s a directed graph. Originally: thought this required time O(|V|*|V|). Can you write an O(|V|) algorithm to find the celebrity? 6

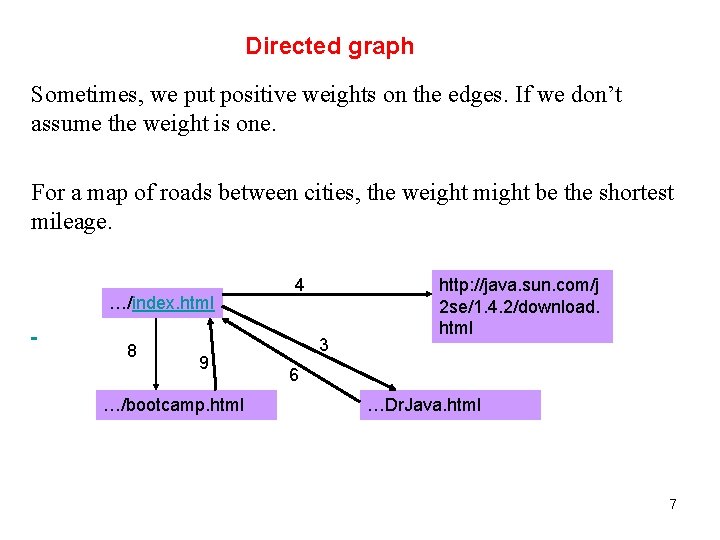
Directed graph Sometimes, we put positive weights on the edges. If we don’t assume the weight is one. For a map of roads between cities, the weight might be the shortest mileage. …/index. html 8 9 …/bootcamp. html 4 3 http: //java. sun. com/j 2 se/1. 4. 2/download. html 6 …Dr. Java. html 7

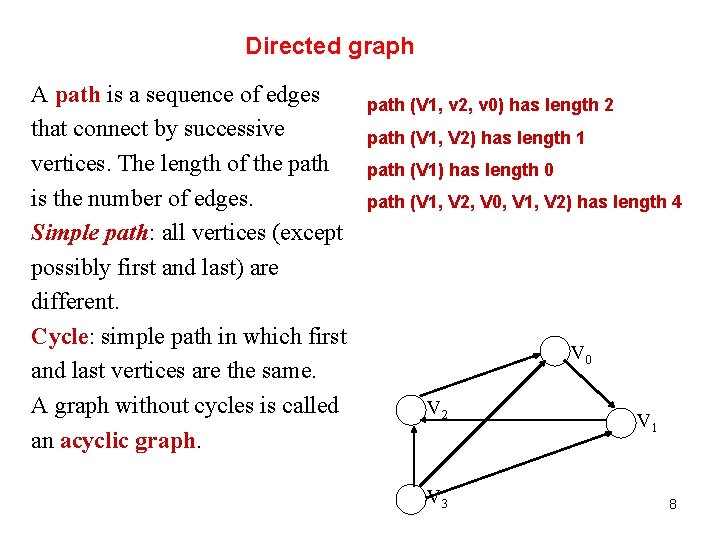
Directed graph A path is a sequence of edges that connect by successive vertices. The length of the path is the number of edges. Simple path: all vertices (except possibly first and last) are different. Cycle: simple path in which first and last vertices are the same. A graph without cycles is called an acyclic graph. path (V 1, v 2, v 0) has length 2 path (V 1, V 2) has length 1 path (V 1) has length 0 path (V 1, V 2, V 0, V 1, V 2) has length 4 V 0 V 2 V 3 V 1 8
![Adjacency matrix representation of a digraph Use a boolean array b0 V10 Adjacency matrix: representation of a digraph Use a boolean array b[0. . |V|-1][0. .](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-9.jpg)
Adjacency matrix: representation of a digraph Use a boolean array b[0. . |V|-1][0. . |V|– 1] b[r][c] = “there is an edge from Vr to Vc” 0 1 2 3 Constant time to tell whethere is an edge from r to c. Good. 0 F T F F Takes |V|*|V| time to construct, |V|*|V| space, and |V|*|V| time to process all edges. 2 T F F F No good if graph is sparse (very few edges in relation to number of nodes). Usually, sparse means that the number of edges is O(|V|). 1 F F T F 3 T T T F V 0 V 2 V 3 V 1 9
![Adjacency list representation of a Use array b0 V 1 of linked lists Adjacency list: representation of a Use array b[0. . |V|– 1] of linked lists](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-10.jpg)
Adjacency list: representation of a Use array b[0. . |V|– 1] of linked lists digraph for sparse graphs If (h, k) is an edge, k is on linked list b[h]. 0 1 2 3 V 0 1 V 2 2 0 1 V 3 0 2 No prescribed order of values in a linked list. Time to construct: O(|V|) + O(|E|) Time to tell whether an edge is there: O(|V|) (worst case) Time to process the edges: O(|E|) 10

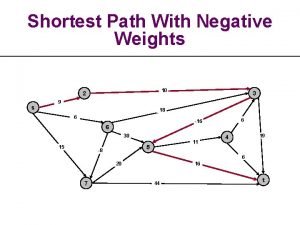
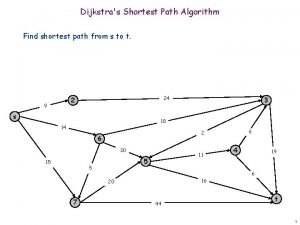
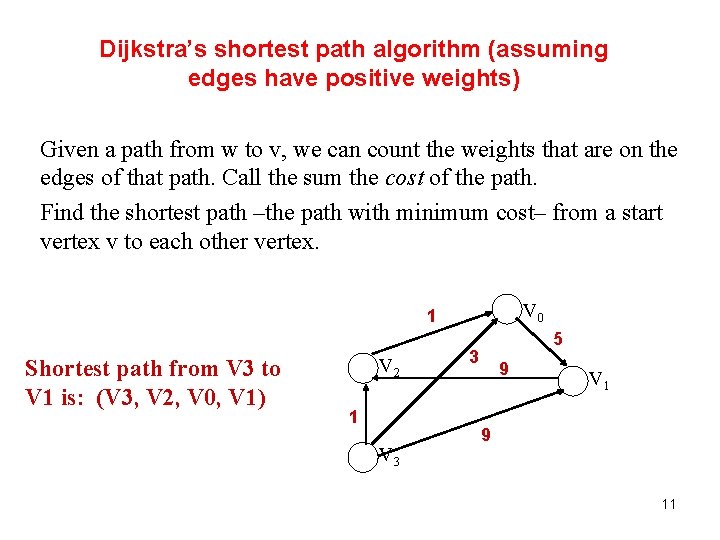
Dijkstra’s shortest path algorithm (assuming edges have positive weights) Given a path from w to v, we can count the weights that are on the edges of that path. Call the sum the cost of the path. Find the shortest path –the path with minimum cost– from a start vertex v to each other vertex. V 0 1 Shortest path from V 3 to V 1 is: (V 3, V 2, V 0, V 1) V 2 1 V 3 5 3 9 V 1 9 11

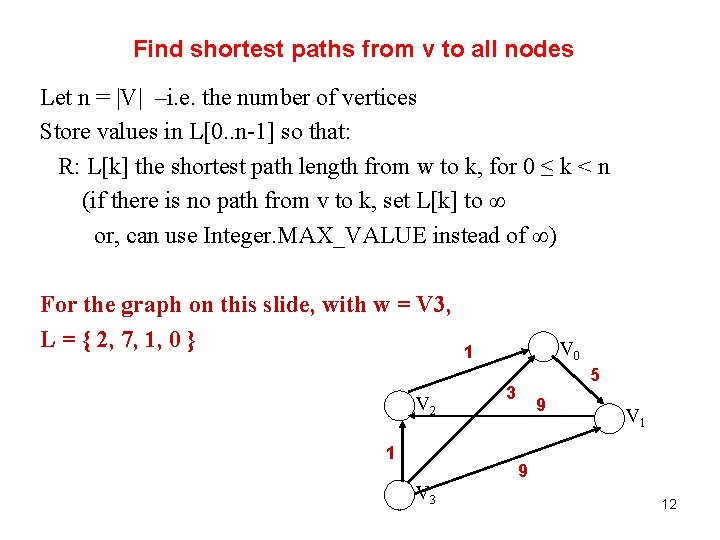
Find shortest paths from v to all nodes Let n = |V| –i. e. the number of vertices Store values in L[0. . n-1] so that: R: L[k] the shortest path length from w to k, for 0 ≤ k < n (if there is no path from v to k, set L[k] to ∞ or, can use Integer. MAX_VALUE instead of ∞) For the graph on this slide, with w = V 3, L = { 2, 7, 1, 0 } V 2 1 V 3 V 0 1 5 3 9 V 1 9 12
![Find shortest paths from v to all nodes Initially Lv 0 Lw Find shortest paths from v to all nodes Initially, L[v] = 0 L[w] =](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-13.jpg)
Find shortest paths from v to all nodes Initially, L[v] = 0 L[w] = ∞ red set = {} 3 4 v 1 // shortest path from v to v // for all other nodes red set: the set of vertices (1) whose L-value has been calculated (2) whose neighbors have L-values < ∞ (3)Frontier: vertices that (4) are not in the red set (5) have L-value < ∞ 13
![Find shortest paths from v to all nodes Initially Lv 0 shortest Find shortest paths from v to all nodes Initially, L[v] = 0 // shortest](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-14.jpg)
Find shortest paths from v to all nodes Initially, L[v] = 0 // shortest path from v to v We put the L-values in the nodes themselves. 3 3 v 0 4 1 2 14 3 6 red set: the set of vertices (1) whose L-value has been calculated (2) whose neighbors have L-values < ∞ (3)Frontier: vertices that (4) are not in the red set (5) have L-value < ∞ For a node w in Frontier, L[w] is the minimum path length over (v, w) paths using only red nodes (except for w). 14
![Find shortest paths from v to all nodes Initially Lv 0 shortest Find shortest paths from v to all nodes Initially, L[v] = 0 // shortest](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-15.jpg)
Find shortest paths from v to all nodes Initially, L[v] = 0 // shortest path from v to v We put the L=values in the nodes themselves. 3 3 4 v 0 1 3 2 1 3 6 7 3 red set: the set of vertices (1) whose L-value has been calculated (2) whose neighbors have L-values < ∞ (3)Frontier: vertices that (4) are not in the red set (5) have L-value < ∞ For a node w in Frontier, L[w] is the minimum path length over (v, w) paths using only red nodes (except for w). 15

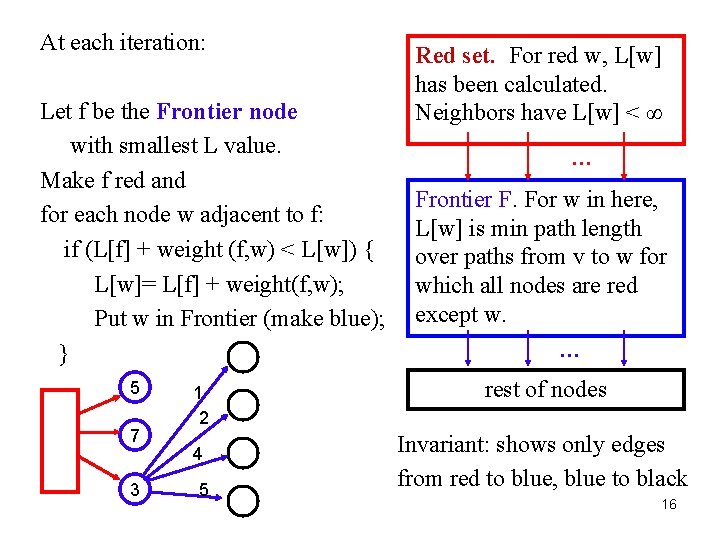
At each iteration: Let f be the Frontier node with smallest L value. Make f red and for each node w adjacent to f: if (L[f] + weight (f, w) < L[w]) { L[w]= L[f] + weight(f, w); Put w in Frontier (make blue); } 5 7 3 1 2 4 5 Red set. For red w, L[w] has been calculated. Neighbors have L[w] < ∞ … Frontier F. For w in here, L[w] is min path length over paths from v to w for which all nodes are red except w. … rest of nodes Invariant: shows only edges from red to blue, blue to black 16
![Lw for all nodes w Lv 0 F v while F not empty L[w]= ∞ for all nodes w; L[v]= 0; F= {v}; while (F not empty)](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-17.jpg)
L[w]= ∞ for all nodes w; L[v]= 0; F= {v}; while (F not empty) { f= a node in F with min L value; Make f red (delete from F); for each node w adjacent to f: if (L[f] + weight (f, w) < L[w]) { L[w]= L[f] + weight(f, w); if (w is not in F) put w in F; } 5 } 1 7 3 Red set. For red w, L[w] has been calculated. Neighbors have L[w] < ∞ … Frontier F. For w in here, L[w] is min path length over paths from v to w for which all nodes are red except w. … rest of nodes 2 4 5 Invariant: shows only edges from red to blue, blue to black 17
![Lw for all nodes w How much time Lv 0 F v while L[w]= ∞ for all nodes w; How much time? L[v]= 0; F= {v}; while](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-18.jpg)
L[w]= ∞ for all nodes w; How much time? L[v]= 0; F= {v}; while (F not empty) { // outer loop: |V| iterations f= a node in F with min L value; // done |V| times Make f red (delete from F); // done |V| times for each node w adjacent to f: if (L[w] = ∞) { // done |E| times L[w]= L[f] + weight(f, w); // done < |V| times Put w in F; // done < |V| times } else if (L[f] + weight (f, w) < L[w]) // done < |E| – |V| times L[w]= L[f] + weight(f, w); // done < |E| – |V| times } 5 7 3 1 2 4 5 What data structure do we use for F? 18
![Lw for all nodes w Lv 0 F v while F not empty L[w]= ∞ for all nodes w; L[v]= 0; F= {v}; while (F not empty)](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-19.jpg)
L[w]= ∞ for all nodes w; L[v]= 0; F= {v}; while (F not empty) { f= a node in F with min L value; Make f red (delete from F); for each node w adjacent to f: if (L[w] = ∞) { L[w]= L[f] + weight(f, w); Put w in F; } else if (L[f] + weight (f, w) < L[w]) L[w]= L[f] + weight(f, w); } 5 7 3 1 2 4 5 What data structure do we use for F? A min-heap --a heap with minimum at the top. f= node with min L value: constant time Delete f from F: log |F| time Put w in F: log |F| time Total time: O(|V| log |V|) 19

/** An instance is an edge */ public class Edge { public int start; // An edge from vertex start public int end; // to vertex end public int weight; // the weight of the edge (> 0) /** Constructor: and edge (start, end) with weight w */ public Edge(int start, int end, int w) { this. start= start; this. end= end; weight= w; } } 20
![public class Adjacency List private LNode V The adjacency list for the public class Adjacency. List { private LNode[] V; // The adjacency list for the](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-21.jpg)
public class Adjacency. List { private LNode[] V; // The adjacency list for the graph private int Esize; // number of edges /** Constructor: a graph of n nodes, with e edges given by edge set E[0. . e-1]. Precondition: the edges are all different. */ public Adjacency. List(int n, int e, Edge[] E) {} /** = number of nodes in graph */ public int Vsize() {} /** = number of edges in graph */ public int Esize() {} /** = an enumerator over edges with start vertex w next() returns an Edge */ public Iterator adjacency. Enumerator(int w) {} } 21

/** = an array of shortest paths from node v to other nodes in graph g */ public static int[] shortest(Adjacency. List g, int v) { int[] L= new int[g. Vsize()]; // The shortest-path lengths from v for (int k= 0; k != L. length; k= k+1) L[k]= Integer. MAX_VALUE; L[v]= 0; int[] F= new int[g. Vsize()]; // Set F is in min-heap int Fsize= 0; // F[0. . Fsize-1] // Add v to heap F and store the new heap size in Fsize= add. Heap(F, Fsize, v); // Invariant: The red nodes have their L-values calculated and their neighbors have L-values < MAX_VALUE. F is the set of nodes with L-value < MAX_VALUE that are not red. … 22
![while Fsize 0 int f F0 Fsize remove Min HeapF Fsize Iterator while (Fsize != 0) { int f= F[0]; Fsize= remove. Min. Heap(F, Fsize); Iterator](https://slidetodoc.com/presentation_image/c1cbe14174e17e58db67f24096cdbe62/image-23.jpg)
while (Fsize != 0) { int f= F[0]; Fsize= remove. Min. Heap(F, Fsize); Iterator it= g. adjacency. Enumerator(f); while (it. has. Next()) { Edge e= (Edge)it. next(); if (L[e. end] == Integer. MAX_VALUE) { L[e. end]= L[f] + e. weight; Fsize= add. Heap(F, Fsize, e. end); } else { // e. end is already in F if (L[f] + e. weight < L[e. end]) { L[e. end]= L[f] + e. weight; Bubble. Up(F, Fsize, e. end); } } return L; } 23
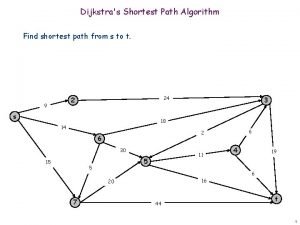
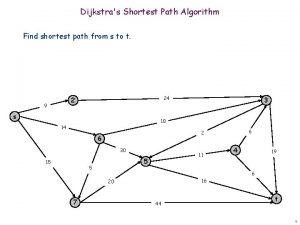
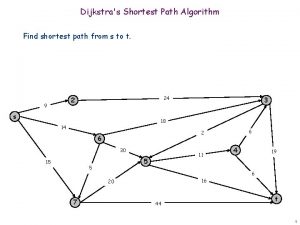
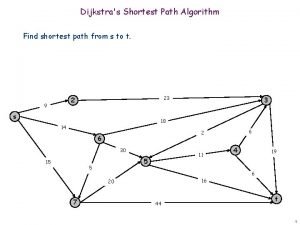
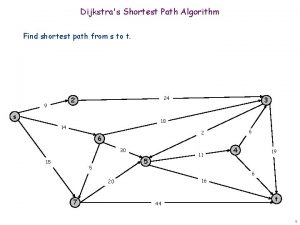
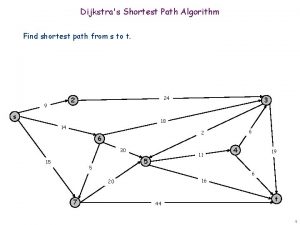
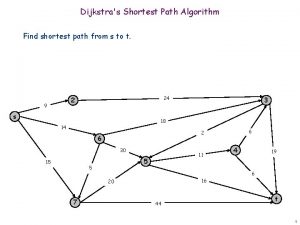
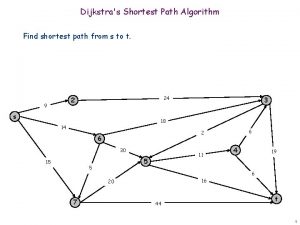
 Dijkstra's shortest path algorithm pseudocode
Dijkstra's shortest path algorithm pseudocode Explain dijkstra algorithm with example
Explain dijkstra algorithm with example Shortest path algorithm in discrete mathematics
Shortest path algorithm in discrete mathematics K shortest path python
K shortest path python Successive shortest path algorithm
Successive shortest path algorithm Length of path
Length of path Shortest path algorithm in mapreduce
Shortest path algorithm in mapreduce Shortest path meaning
Shortest path meaning Shortest path to get food
Shortest path to get food Shortest path problem linear programming
Shortest path problem linear programming Shortest path problem adalah
Shortest path problem adalah Tramp steamer problem
Tramp steamer problem Dijkstra algorithm graph theory
Dijkstra algorithm graph theory Shortest path from source to destination in weighted graph
Shortest path from source to destination in weighted graph Single source shortest path in c
Single source shortest path in c Shortest path problem excel
Shortest path problem excel Minimum spanning tree shortest path
Minimum spanning tree shortest path Find shortest path
Find shortest path Shortest path formulation
Shortest path formulation Neil tang
Neil tang Fme shortest path finder
Fme shortest path finder Shortest path
Shortest path Sssp
Sssp Pathdx
Pathdx