15 053 Tuesday April 2 The Shortest Path

15. 053 Tuesday, April 2 • The Shortest Path Problem • Dijkstra’s Algorithm for Solving the Shortest Path Problem Handouts: Lecture Notes

The Minimum Cost Flow Problem Directed Graph G = (N, A). A network with costs, capacities, supplies, demands Node set N, arc set A; Capacities uij on arc (i, j) Lower bound of 0 on arc (i, j) Cost cij on arc (i, j) Supply/demand bi for node i. (Positive indicates supply) Minimize the cost of sending flow s. t. Flow out of i - Flow into i = bi 0 ≤xij ≤uij

Formulation In general the LP formulation is given as Minimize subject to

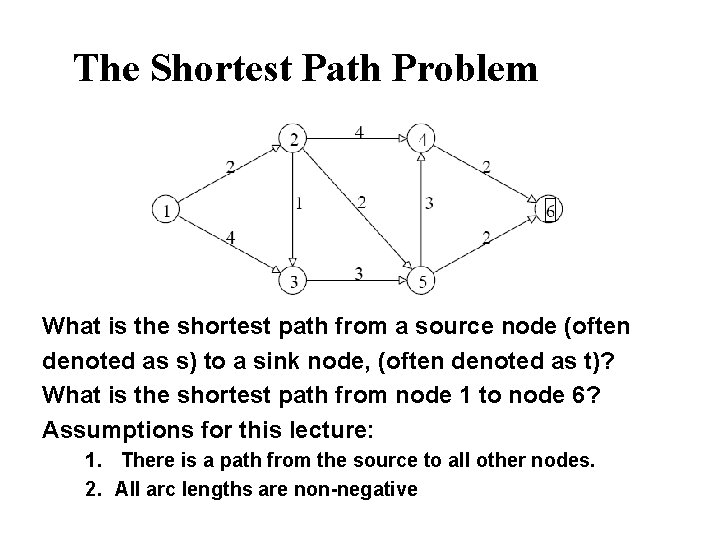
The Shortest Path Problem What is the shortest path from a source node (often denoted as s) to a sink node, (often denoted as t)? What is the shortest path from node 1 to node 6? Assumptions for this lecture: 1. There is a path from the source to all other nodes. 2. All arc lengths are non-negative

Formulation as a linear program In general the LP formulation for the shortest path from a source, s, to a sink, t, is given as Minimize subject to

Another Formulation The LP formulation for the shortest path from a source, s, to all other nodes is given as Minimize subject to

Some Questions Concerning the Shortest Path Problem • Where does it arise in practice? – Direct applications – Indirect (and often subtle) applications • How does one solve the shortest path problem? – Dijkstra’s algorithm • How does one measure the performance of an algorithm? – CPU time measurements – Performance Guarantees • How does one establish that a solution is really the shortest path? – Connection to LP duality

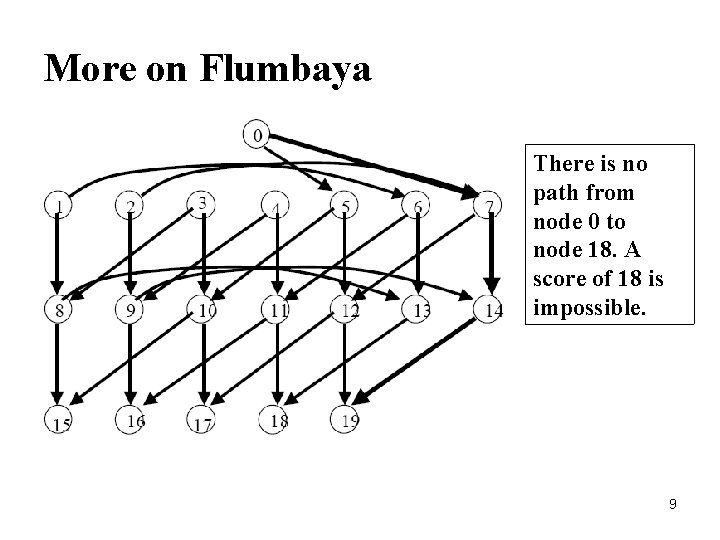
Possible sports scores • Flumbaya is an unusual water sport in which there are two types of scores possible. One can score a gymbol, which is worth 7 points, or one can score a quasher, which is worth 5 points. An announcer on TV states that a recent game was won by a score of 19 to 18. Is this possible?

More on Flumbaya There is no path from node 0 to node 18. A score of 18 is impossible. 9

More on Flumbaya Data: Gymbol is worth n 1 points Quasher is worth n 2 points: determine whether one can score q points The network: G = (N, A), where N = {0, …, q} for each node j = 0 to q – n 1 , (j, j+n 1) ∈ A for each node j = 0 to q – n 2, (j, j+n 2) ∈ A Question: Is there a path in G from node 0 to node q? Fact: if n 1 and n 2 have no common integer divisor (other than 1 and – 1), then the number of scores that cannot be obtained is (n-1)(n 2 -1)/2. Extra credit for proving this fact. (Warning, it is difficult to prove. )

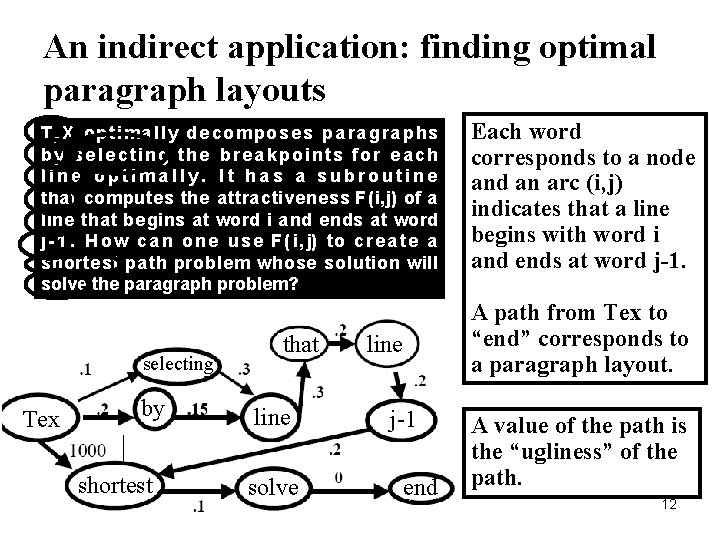
An indirect application: Finding optimal paragraph layouts T e. X o p ti ma l l y d e co mp o se s p a ra g ra p h s b y se le cting the bre a kpoints for e a ch line optima lly. I t ha s a subroutine tha t compute s the a ttra ctive ne ss F ( i, j) of a line tha t be gins a t word i a nd e nds a t word j- 1. H ow ca n one u s e F ( i, j) to cre a te a shorte st pa th proble m whose solution will solve the pa ra gra ph problem? T e. X o p t i m a l l y d e c o m p o s e s p a r a g r a p h s by se le cting the bre a kpoints for e a ch line optimally. It has a subroutine tha t compute s the a ttra ctive ne ss F ( i, j) of a line tha t be gins a t word i a nd e nds a t word j - 1. H o w c a n o n e u s e F ( i , j) t o c r e a t e a shorte st pa th proble m whose solution will solve the paragraph problem? 11

An indirect application: finding optimal paragraph layouts T e X optima lly de compose s pa ra gra phs by se le cting the bre a kpoints for e a ch line optima lly. I t ha s a subroutine that computes the attractiveness F(i, j) of a line that begins at word i and ends at word j - 1. H o w c a n o n e u s e F ( i, j) to cre a te a shortest path problem whose solution will solve the paragraph problem? selecting Tex by shortest that line solve line j-1 end Each word corresponds to a node and an arc (i, j) indicates that a line begins with word i and ends at word j-1. A path from Tex to “end” corresponds to a paragraph layout. A value of the path is the “ugliness” of the path. 12

On the paragraph example • n different yes-no decisions – Decision j: Yes means start a line at word j – No: don’t start a line at word j • The cost of each yes decision depends only on the subsequent yes decision – f(i, j) was the cost of starting a line at word i assuming that word j begins the next line. • Create a shortest path problem with nodes 1, 2, … , n+1 where the cost of arc (i, j) is f(i, j). What is the shortest path from 1 to n+1

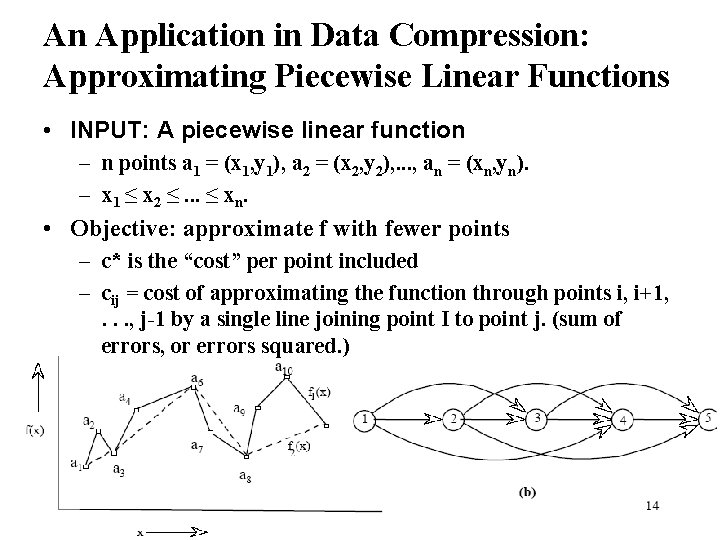
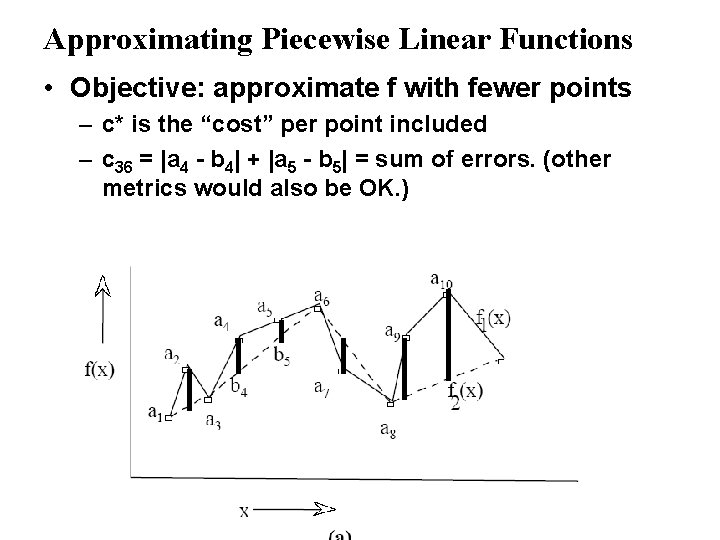
An Application in Data Compression: Approximating Piecewise Linear Functions • INPUT: A piecewise linear function – n points a 1 = (x 1, y 1), a 2 = (x 2, y 2), . . . , an = (xn, yn). – x 1 ≤ x 2 ≤. . . ≤ xn. • Objective: approximate f with fewer points – c* is the “cost” per point included – cij = cost of approximating the function through points i, i+1, . . . , j-1 by a single line joining point I to point j. (sum of errors, or errors squared. )

Approximating Piecewise Linear Functions • Objective: approximate f with fewer points – c* is the “cost” per point included – c 36 = |a 4 - b 4| + |a 5 - b 5| = sum of errors. (other metrics would also be OK. )

On approximating functions • n different yes-no decisions – Decision j: yes means select point j – No: don’t select point j • The cost of each yes decision depends only on the subsequent yes decision – cij is the cost of selecting point i followed by point j, and takes into account the cost of selecting i, and the costs of approximating points i+1, …, j-1. • Create a shortest path problem with nodes 1, … , n where the cost of arc (i, j) is cij. What is the shortest path from 1 to n?

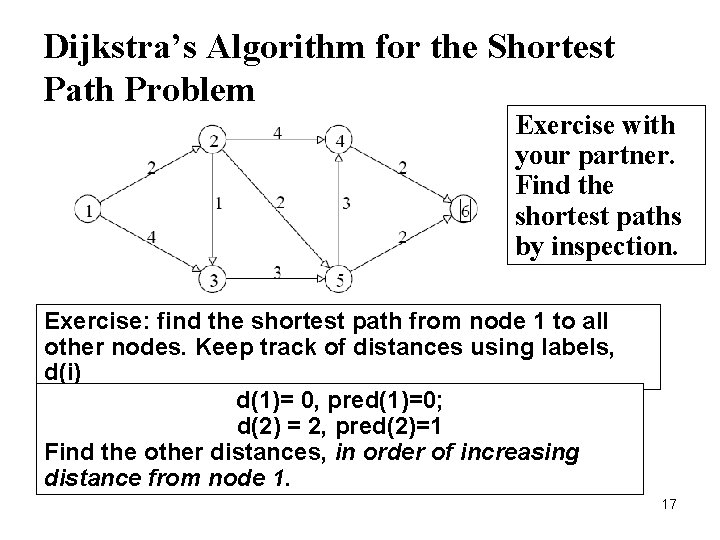
Dijkstra’s Algorithm for the Shortest Path Problem Exercise with your partner. Find the shortest paths by inspection. Exercise: find the shortest path from node 1 to all other nodes. Keep track of distances using labels, d(i) and each node’s d(1)= immediate predecessor, pred(i). 0, pred(1)=0; d(2) = 2, pred(2)=1 Find the other distances, in order of increasing distance from node 1. 17

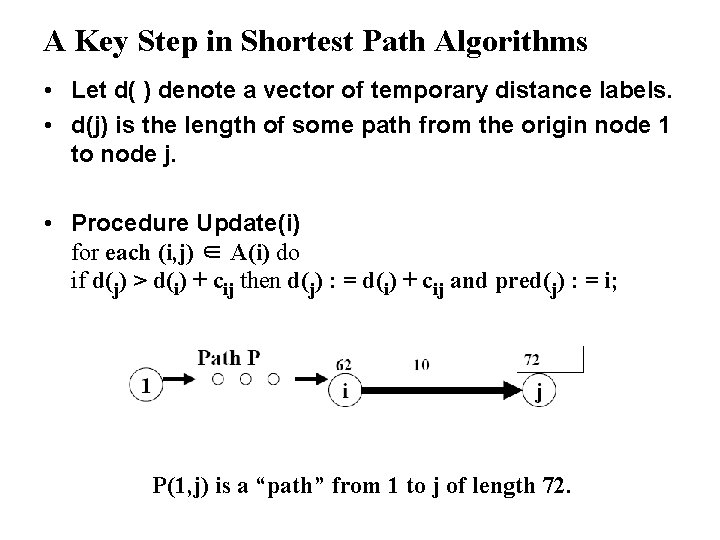
A Key Step in Shortest Path Algorithms • Let d( ) denote a vector of temporary distance labels. • d(j) is the length of some path from the origin node 1 to node j. • Procedure Update(i) for each (i, j) ∈ A(i) do if d(j) > d(i) + cij then d(j) : = d(i) + cij and pred(j) : = i; Up to this point, the best path from 1 to j has length 78

A Key Step in Shortest Path Algorithms • Let d( ) denote a vector of temporary distance labels. • d(j) is the length of some path from the origin node 1 to node j. • Procedure Update(i) for each (i, j) ∈ A(i) do if d(j) > d(i) + cij then d(j) : = d(i) + cij and pred(j) : = i; P(1, j) is a “path” from 1 to j of length 72.

Dijkstra’s Algorithm begin d(s) : = 0 and pred(s) : = 0; d(j) : = ∞ for each j ∈ N - {s}; LIST : = {s}; while LIST ≠ φ do begin let d(i) : = min {d(j) : j ∈ LIST}; remove node i from LIST; update(i) if d(j) decreases, place j in LIST end Initialize distances. LIST = set of temporary nodes Select the node i on LIST with minimum distance label, and then update(i) 20

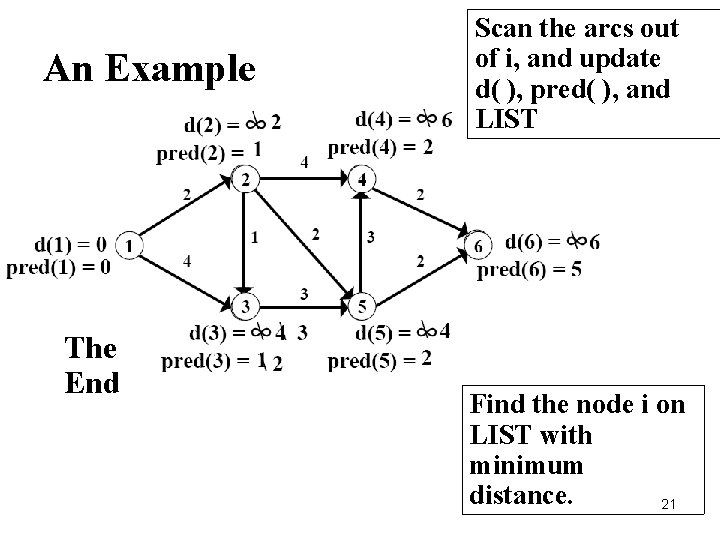
An Example The End Scan the arcs out of i, and update d( ), pred( ), and LIST Find the node i on LIST with minimum distance. 21

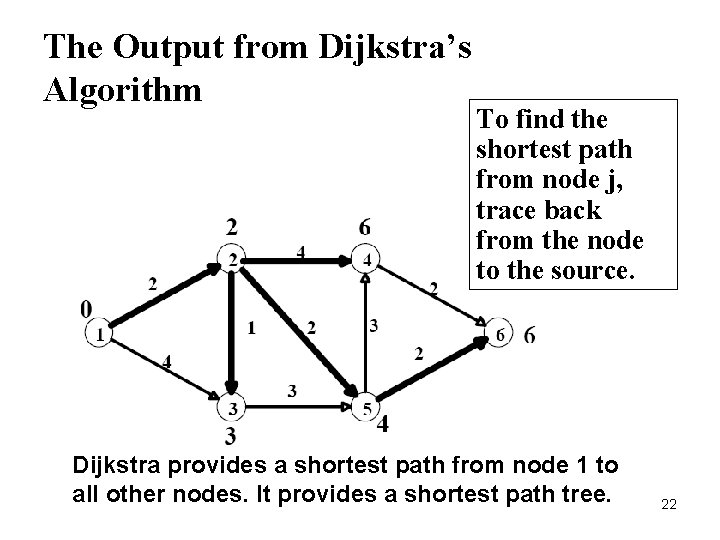
The Output from Dijkstra’s Algorithm To find the shortest path from node j, trace back from the node to the source. Dijkstra provides a shortest path from node 1 to all other nodes. It provides a shortest path tree. 22

Comments on Running time • Dijkstra’s algorithm is efficient in its current form. The running time grows as n 2. • It can be made much more efficient • In practice it runs in time linear in the number of arcs (or almost so).

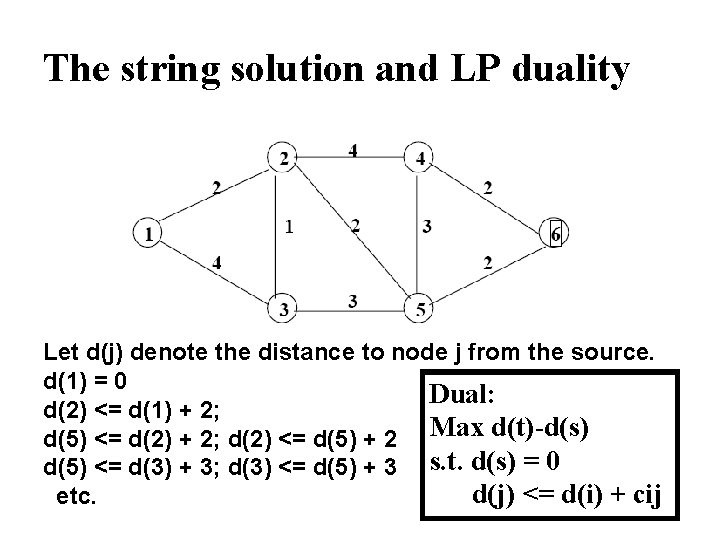
The string solution and LP duality Let d(j) denote the distance to node j from the source. d(1) = 0 Dual: d(2) <= d(1) + 2; d(5) <= d(2) + 2; d(2) <= d(5) + 2 Max d(t)-d(s) d(5) <= d(3) + 3; d(3) <= d(5) + 3 s. t. d(s) = 0 d(j) <= d(i) + cij etc.

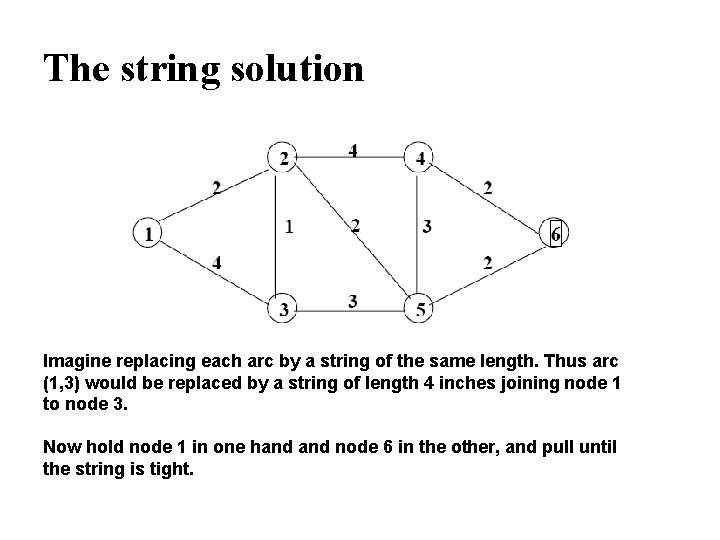
The string solution Imagine replacing each arc by a string of the same length. Thus arc (1, 3) would be replaced by a string of length 4 inches joining node 1 to node 3. Now hold node 1 in one hand node 6 in the other, and pull until the string is tight.

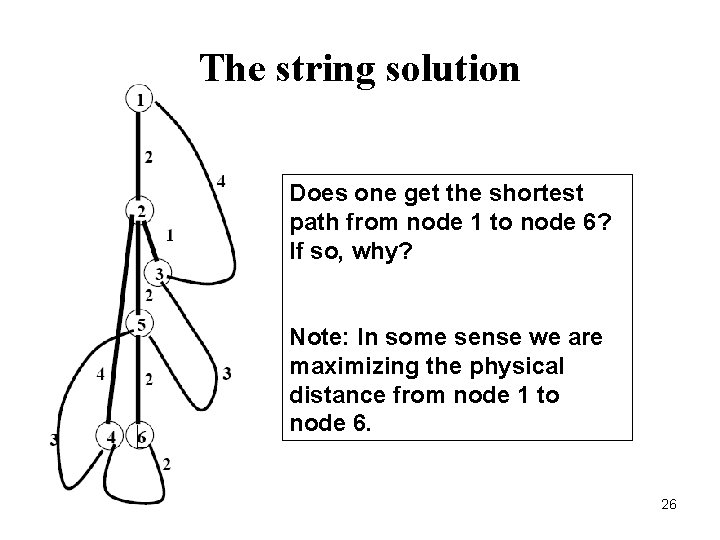
The string solution Does one get the shortest path from node 1 to node 6? If so, why? Note: In some sense we are maximizing the physical distance from node 1 to node 6. 26

Summary • Direct and indirect applications for the shortest path problem • Dijkstra’s algorithm finds the shortest path from node 1 to all other nodes in increasing order of distance from the source node. • The bottleneck operation is identifying the minimum distance label. One can speed this up, and get an incredibly efficient algorithm • The string solution optimizes the dual LP as well as the shortest path problem.

Some final comments • The shortest path problem shows up again and again in network optimization • There is an interesting connection with dynamic programming • There are other solution techniques as well. We’ll see one in a later lecture.