Control Systems and Adaptive Process Regulators and Communication

Control Systems and Adaptive Process. Regulators and Communication 1

Controllers and calibration • To design a controller the specifications should not be more stringent than necessary. • The subsequent controller calibration will adjust their response when changes in the starting model or plant elements. • The method of designing a control system depends on the type of system and how are presented the specifications. 2

Controllers and calibration • For systems with a single input and a single output, the most basic method is estimating and modification, in which is designed a model that is able to perform the appropriate task. • At other times there are parts of a system which does not change, on which cannot act, forcing to use other mode to modify or compensate the system. • A first step in compensation is the variation of the open loop gain, but this method is not always valid because it has limitations. In other cases it’s necessary to introduce compensators. 3

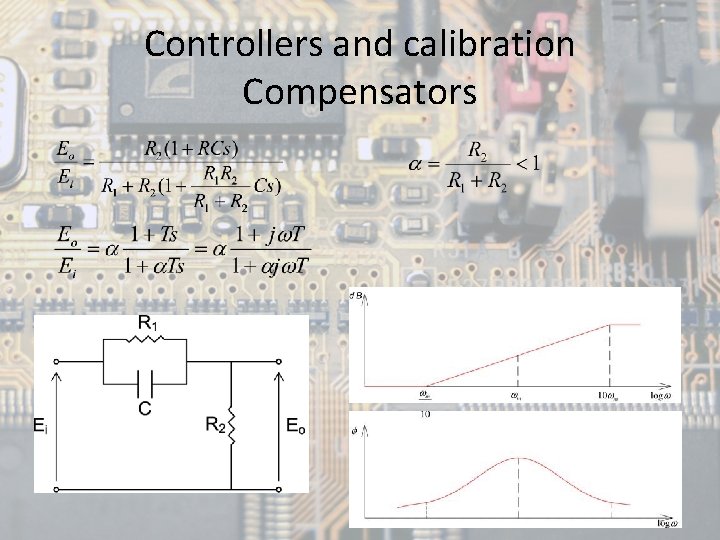
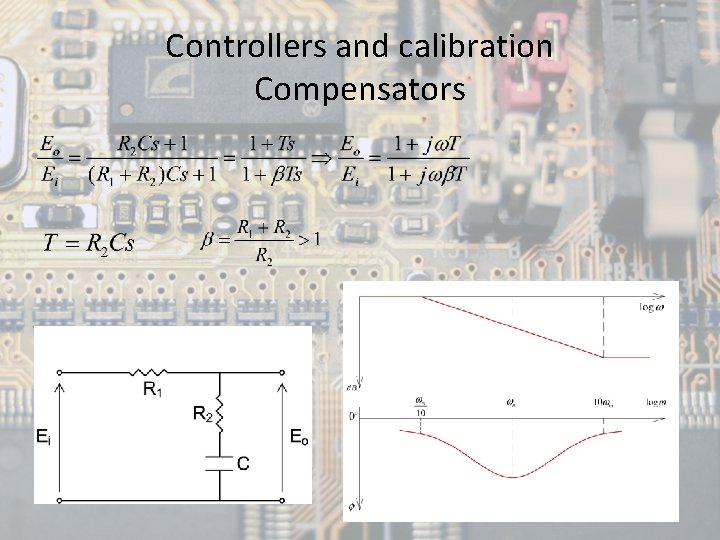
Controllers and calibration Compensators • Compensators: devices inserted into the system to improve the stability of a control system. • The compensation of control systems is done mainly by a fixed configuration in which the controller is placed at a certain point in the system, talking serial compensation, feedback, or by feedback of state variables, each of them presenting advantages and drawbacks 4

Controllers and calibration Compensators • There are three types of compensators according to the needs as they arise: – Lead compensators – Lag-lead compensators 5

Controllers and calibration Compensators • Lead phase compensators: those in which the steady-state output has a phase advance with respect to the input. Improves system stability without changing the accuracy. Increases by one the order of the system. – The maximum phase advance ɸm will be determined by the tangent to the circle and will be produced when – The slope of the transfer curve is 6 d. B/oct. 6

Controllers and calibration Compensators 7

Controllers and calibration Compensators • Lag compensators: if the steady-state output phase has a delay with respect to the input. Improves steady state response without changing the transient response. Increases by one the order of the system. – The slope of the transference curve is -6 d. B/oct. 8

Controllers and calibration Compensators 9

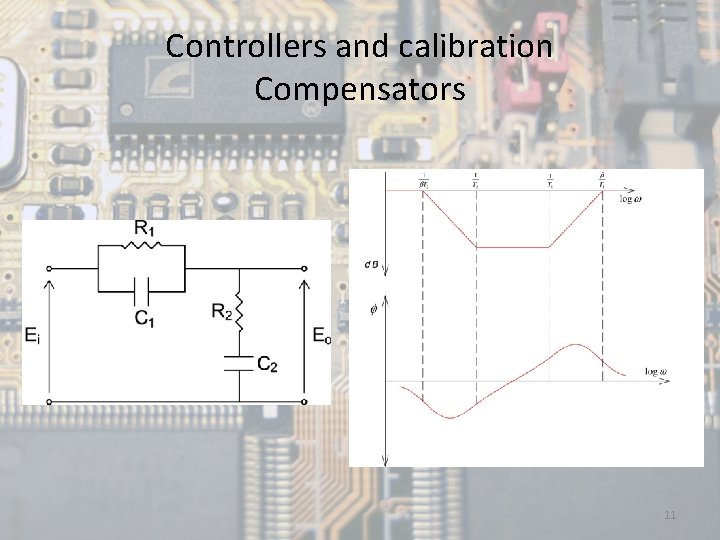
Controllers and calibration Compensators • Lead-lag compensators: are those in that appear a delay and a phase advance, but in different frequency regions. The delay occurs in the low frequency region and the advancement in the high frequency region. Increase in two units the order of the system. 10

Controllers and calibration Compensators 11

Controllers and calibration Calibration rules • For calibration of control systems are used various methods. Among these, the most used are the methods of root locus approach and frequency response. • Each of these methods will be applied differently when using lead, lag or lead-lag compensators. : 12

Controllers and calibration Calibration rules Root Locus approach: • It is called root locus to the geometrical place of the G(s) poles by varying the value of the gain (or other parameter of the system) from zero to infinity or in a certain range. • The root locus approach allows to know how affects the open-loop gain in the behavior of a system with feedback (stability, oscillations, speed to vary the gain). Normally is used only when there are transient response specifications. 13

Controllers and calibration Calibration rules Root Locus approach: example 14

Controllers and calibration Calibration rules • • • The closed-loop poles correspond to the roots of the characteristic equation, but these poles vary when vary the gain, so that the calculation should be repeated for any change in the value of this parameter. In 1948 W. R. Evans developed a method for its calculation which permit to draw the roots of the 7 characteristic equation for all values of a parameter. It is about knowing in what place are the poles of the transfer function of a system depending of a parameter, usually the gain. By this method the designer can know the effects they will have on the system the gain or the addition of zeros and poles. Basically, to calibrate a system using this method, the root locus is reconstructed by a compensator, so that they can be placed dominant closed-loop poles at the desired position to get the system be stable and meets the required specifications. The addition of zeros to the system moves the closed-loop poles to the left, making the system more stable. Adding open-loop poles, the existing poles move to the right and stability worsens. The determination of the root locus is a laborious task. At present there are computer programs that allow their determination by a simple programming, for example the free software Scilab. 15

Controllers and calibration Calibration rules Being a feedback system such that: to calculate the poles of the transfer function the denominator must be equal to zero, so that 16

Controllers and calibration Calibration rules • To draw the root locus must follow these rules: 1. - The number of branches is equals to the number of poles of the transfer function in open loop. 2. - Each branch starts at one pole (ks=0) and ends at a zero (ks=∞). If the number of zeros z is less than the number of poles p, will exist p-z zeros at infinity, towards will go p-z branches following p-z asymptotes. 3. - Real axis points with an odd number of poles and zeros to the right belong to the geometrical locus of the roots (ks>0), and if even, to the reverse place (ks<0), taking into account that both sites are symmetric about the real axis. 4. - The p-z asymptotes intersecting at point: 17

Controllers and calibration Calibration rules 5. - The angles of the asymptotes with real axis are obtained by the expressions: siendo q= 0, 1, 2, . . . , p-z-1 6. - The exit angles of the poles and arrival of the zeros are obtained by applying the criterion of the argument. being q= 0, 1, 2, . . . , p-z-1 18

Controllers and calibration Calibration rules 7. - The breakpoints are those where the geometrical locus between two poles leave the real axis and are determined by 8. - The intersection points of the root locus with the imaginary axis are calculated using the Routh criterion of the characteristic equation, or replacing s by jω in that equation and obtaining the values of ω and k, equaling real and imaginary parts to zero. 9. - The gain at any point of the root locus can be calculated applying the expression: 19

Controllers and calibration Calibration rules • This technique can be adapted to other parameters different than the gain. • Once we know the root locus of the system, we must take into account the • characteristics ξ and ωn of transient response. • To achieve the specifications have to see if the root locus passes through the points defined by these parameters and, if they do not, make them to pass. This method is only used when there are transient response specifications. 20

Controllers and calibration Calibration rules Frequency-Response Analysis: • With this method on analyse the steady-state response of a system to a sinusoidal input by varying her frequency over a certain range. This method provides information on the frequency response of the plant. • Basically on use the Bode diagrams and Nyquist plot. 21

Controllers and calibration Calibration rules • From the diagrams in function of frequency are determined a number of features of the system. The transient adjustment is done by successive approximations. Depending on the required characteristics will be used one or other diagram. • These methods have the advantage that it is not necessary to know the transfer function of the plant. Also provides information about its frequency response: - Low frequency: gives an idea of the accuracy and allows to calculate the static coefficients. - Mid frequencies: this allows to know the stability, frequency margin, gain margin and transient response. - High frequency: gives an idea of the system complexity. 22

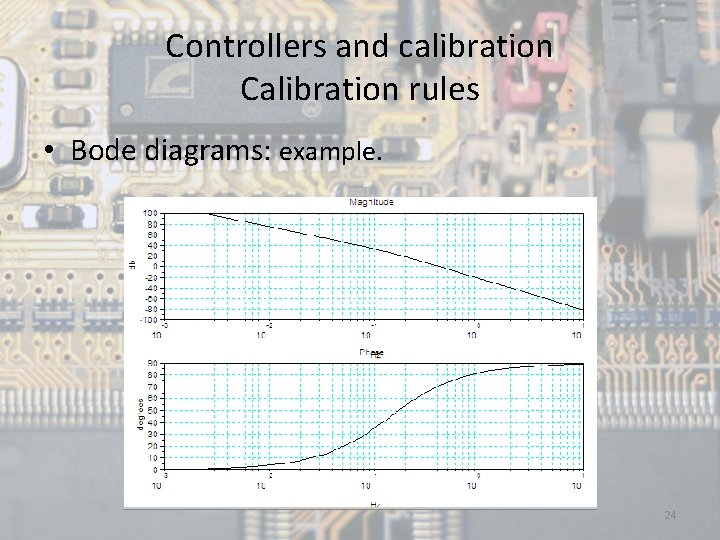
Controllers and calibration Calibration rules Bode diagrams: The Bode diagrams are formed by two graphs versus frequency: the logarithm of the magnitude of the transfer function and the phase angle. • The main advantage of logarithmic representation is that the multiplication of magnitudes becomes a sum, so that its rendering may be carried out knowing as affects each of the terms of the transfer function. For the case of integral and derivative factors, their representation corresponds to straight lines with slopes of 20 d. B/decade and angles of -90° and 90° respectively, so that, analyzing each of the terms, can be performed an asymptotic representation of the exact curve. • Another advantage is that you can make an asymptotic representation in function of the frequency. By working on logarithmic scale may be represented the entire frequency range without reaching zero. 23

Controllers and calibration Calibration rules • Bode diagrams: example. 24

Controllers and calibration Calibration rules • Types of factors that can appear in the representation: - Gain k: In the curve is represented by a constant value 20 log│k│ Si k > 0 → ϕ = 0º Si k < 0 → ϕ = -180º - Integral or derivative factors [jω]± 1: his module is 20 log(ω) Representation 20 d. B/dec or 6 db/oct. 25

Controllers and calibration Calibration rules - First order factor [1+jωT]± 1: The intersection of these two straight lines will occur when ωT=1 The phase of this factor will be: 26

Controllers and calibration Calibration rules - Quadratic factor : Performing mathematical operations: 27

Controllers and calibration Calibration rules • General procedure to represent a curve by the Bode diagram: 1. - It decomposes the sinusoidal function into factors of the types that have seen previously. 2. - We have to observe the different crossover frequencies and find the slope between two consecutive frequencies: If the system is of type 0 the representation begins with a straight line parallel to the real axis. If the system is type 1 begin with a straight line with slope -6 d. B/oct up to the first crossover frequency. If the system is of degree 2, the slope will be -12 d. B/oct. 28

Controllers and calibration Calibration rules • Example: Normalizing this function becomes in: Thus, the crossover frequencies are: 29

Controllers and calibration Calibration rules 30

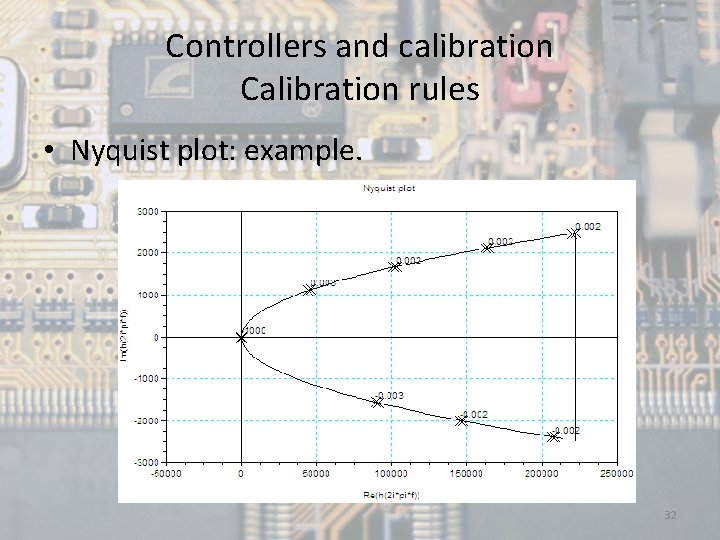
Controllers and calibration Calibration rules Nyquist plot or polar trace: The Nyquist Plot or polar trace is a representation of a magnitude of the transfer function G(jw) (generally gain) respect to the phase angle of this magnitude, when ω vary from zero to infinity. • Therefore the polar trace is the geometrical locus of the vectors when ω vary from zero to infinity. The Nyquist stability criterion relates the open loop frequency response with closed loop stability. An advantage of this graph is that it represents the characteristics of the frequency response in the full spectrum. 31

Controllers and calibration Calibration rules • Nyquist plot: example. 32

Controllers and calibration Calibration rules • Each type of factor of the transfer function has a specific representation: - Integral or derivative factor [jω]± 1: this type of factor is a vector with ω module on the imaginary axis, and positive or negative direction. 33

Controllers and calibration Calibration rules - First order factor [1+jωT]± 1: this factor corresponds to a straight line parallel to the imaginary axis which passes through the point ωT of the real axis. When elevated to -1, corresponds to a semicircle that begins on the real axis and ends in 0. 34

Controllers and calibration Calibration rules - Quadratic factor : its representation starts on the real axis, intersects the imaginary axis at the point 2ξ and continuous with an asymptote for ω=∞. When the quadratic factor is in the denominator its representation begins on the real axis, intersects the imaginary axis at the point ξ/2 and terminates at the point (0, 0). 35

Controllers and calibration Calibration rules • Example of code used on Scilab // Diagrams clear z=poly(0, 'z'); // time vector t=0: 0. 1: 32; // //discret model of the plant g=20/(z*z*(z-0. 9)); // // //open loop transfer function gla=g; glas=syslin('c', gla); // //closed loop transfer function gu=1; glc=gla/. gu; glcs=syslin('c', glc); // //tools programming xset('window', 1) xname('Analysis of the plant with several tools') // 36

//Response to an unitary step //closed loop subplot(2, 2, 1); xgrid(4) plot 2 d(t, csim('step', t, glcs), style=2) xtitle('Response to an unitary step', 'time', 'y(t)') // //Root locus subplot(2, 2, 2); xgrid(4) evans(glas, 2. 5) sgrid([0. 75 0. 4], [0. 5 0. 75], 2) // //Nyquist plot subplot(2, 2, 3) nyquist(glas) // //Bode diagram subplot(2, 2, 4) bode(glas, 0. 001, 10) //---------------------------- 37

Controllers and calibration Calibration rules • Lead compensation techniques based on the method of frequency response analysis - From the Bode plot we want to increase the phase, improving stability, trying to get that maximum phase passes through the crossover frequency. The curve is shifted upwards to not vary the gain at low frequency, multiplying by a factor 1/α: - We try to change or modify the shape of the curve, giving a sufficient degree of phase-lead to offset the excessive phase lag. The steps are: 1. - Determine the value of the open-loop gain to satisfy the specifications for static error constants. 2. - Using the gain K thus determined, obtain the phase margin of the uncompensated system. 3. - Determine the necessary phase-lead angle to be added to the system, calculating ɸmáx. 4. - Determine the attenuation factor α. 5. - Determine the frequency where the magnitude of the uncompensated system has a level of 10 logα. Select this frequency as new gain crossover frequency ωn. 38

Controllers and calibration Calibration rules • Lag compensation techniques based on the method of frequency response analysis Will be necessary to attenuate sufficiently the high frequencies, neither will be interesting that the delay at mid frequencies does not be very large, approaching between them and to the origin the frequencies of the slope change. • The steps to do are: 1. - Determine the open loop gain K to satisfy the static error constants, defined in the requirements 2. - With this K gain value and on the uncompensated system, draw the diagram to obtain MG and MF. 3. - If the uncompensated system does not satisfy the requirements then find the frequency point where the phase angle of the open-loop transfer function is equal to -180º plus the required phase margin Then the curve will be lowered to match the crossover frequency with which it is obtained taking into account the phase introduced by the compensator plus 5° to 12°. 4. - We will match this frequency with the gain crossover frequency this will occur at the right side of the transfer curve of the compensator. From here we will get the value of β. 5. - We need that the highest crossover frequency 1/T will be between 1 octave and a decade lowest to the frequency determined above. 39

Controllers and calibration Calibration rules • Lag-lead compensation techniques based on the method of frequency response analysis • The steps are as follows: 1. - Determine the gain of the system to satisfy the static error constants. 2. - Draw the gain curve and observe if satisfy the requirements. 3. - Determine the lag compensator needed, and calculate the new crossover frequency. 4. - On this new frequency introduce the lead phase. In this type of compensator, once defined β, will only have to define the distance between frequencies, that is, move T 1 with respect to T 2 so desired. In any case you should use physically realizable time constants. 40

Controllers and calibration Functional test • Once implemented the system of compensation or control it is necessary to perform the adequate tests to verify the compliance with the design specifications. The tests to be performed depends on the type of compensator, the type of process and the type of specifications or requirements. 41

Bibliography • K. Ogata, Modern Control Engineering. Interesting links • • • • http: //www. scilab. org/ http: //www. ie. itcr. ac. cr/gaby/Control_Automatico/Presentaciones/12_Control. Comp ensador. Atraso. Rlocus. Continuo_v 12 s 01. pdf http: //www. eis. uva. es/~eduzal/icontrol/compen. pdf http: //www 1. ceit. es/asignaturas/control 1/2000 feb 1. html http: //isa. uniovi. es/~chema/regma_archivos/lr. pdf http: //isa. uniovi. es/docencia/ra_marina/UCLM_TEMA 9. PDF http: //iele. edii. uclm. es/Estudios/ITIE/Albacete/Asignaturas/RA_archivos/A_Descar ga/Transparencias/Tema 09. pdf http: //ingenieria. udea. edu. co/~jbuitrago/instrumentacion. Electronica/Clases/Clase 0 3%20 y%2004 -Diagrama%20 de%20 Nyquist-Estabilidad. pdf http: //sel. uady. mx/ingenieria/courses/CONI/document/Unidad 5/Notas. Control_5_Lu gar. Raices. pdf? cid. Req=CONI http: //ecee. colorado. edu/copec/book/slides/Ch 9 slide. pdf http: //www. cs. mun. ca/av/old/teaching/cs/notes/rlocus 1_quad. pdf 42