Contents A 9 Graphs of nonlinear functions A


- Slides: 23

Contents A 9 Graphs of non-linear functions A A 9. 1 Plotting curved graphs A A 9. 2 Graphs of important non-linear functions A A 9. 3 Using graphs to solve equations A A 9. 4 Solving equations by trial and improvement A A 9. 5 Function notation A A 9. 6 Transforming graphs 1 of 48 © Boardworks Ltd 2005

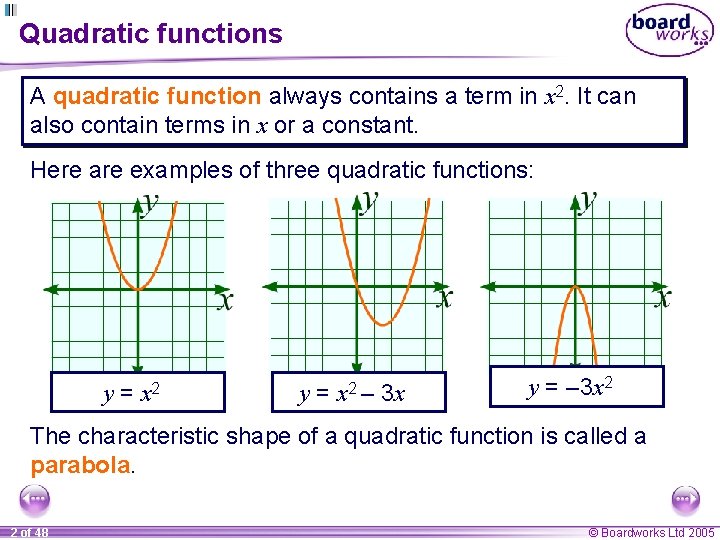
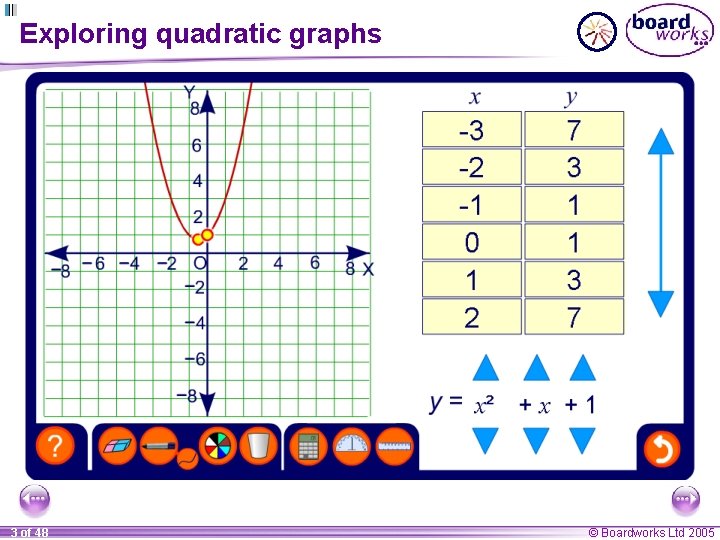
Quadratic functions A quadratic function always contains a term in x 2. It can also contain terms in x or a constant. Here are examples of three quadratic functions: y= x 2 – 3 x y = – 3 x 2 The characteristic shape of a quadratic function is called a parabola. 2 of 48 © Boardworks Ltd 2005

Exploring quadratic graphs 3 of 48 © Boardworks Ltd 2005

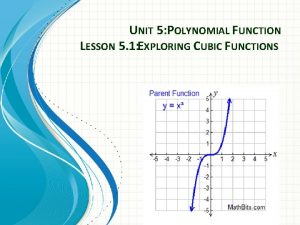
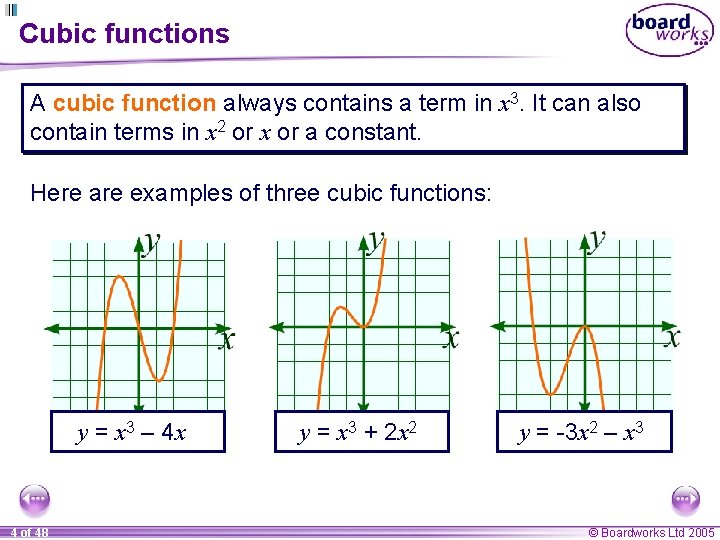
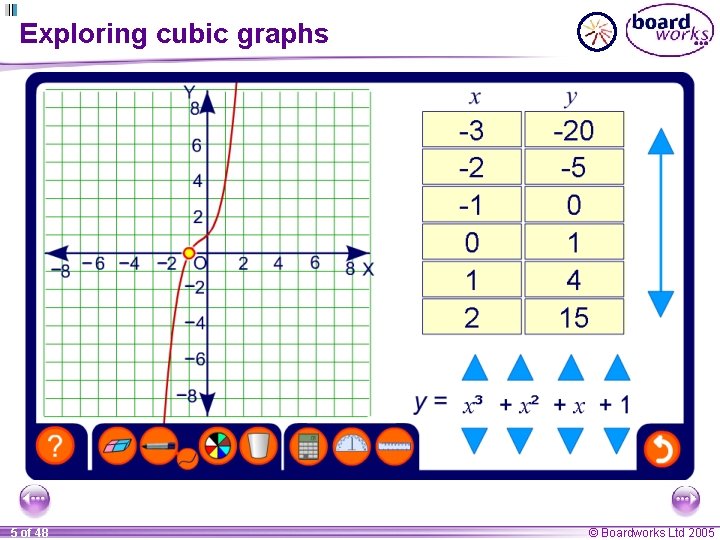
Cubic functions A cubic function always contains a term in x 3. It can also contain terms in x 2 or x or a constant. Here are examples of three cubic functions: y = x 3 – 4 x 4 of 48 y = x 3 + 2 x 2 y = -3 x 2 – x 3 © Boardworks Ltd 2005

Exploring cubic graphs 5 of 48 © Boardworks Ltd 2005

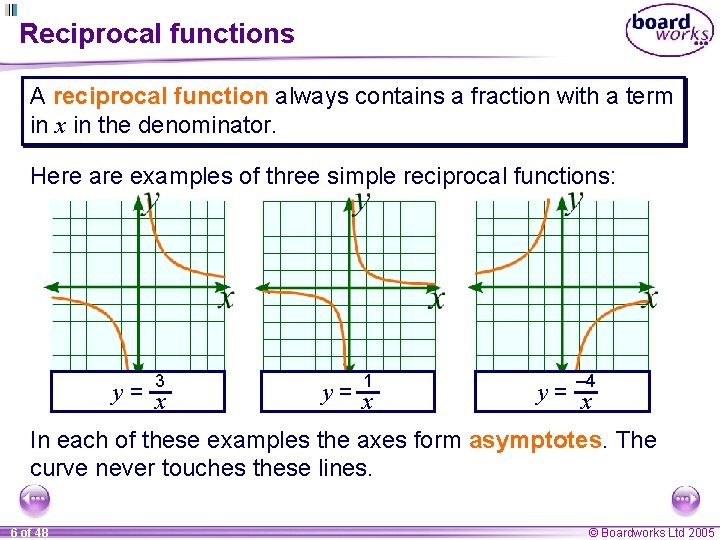
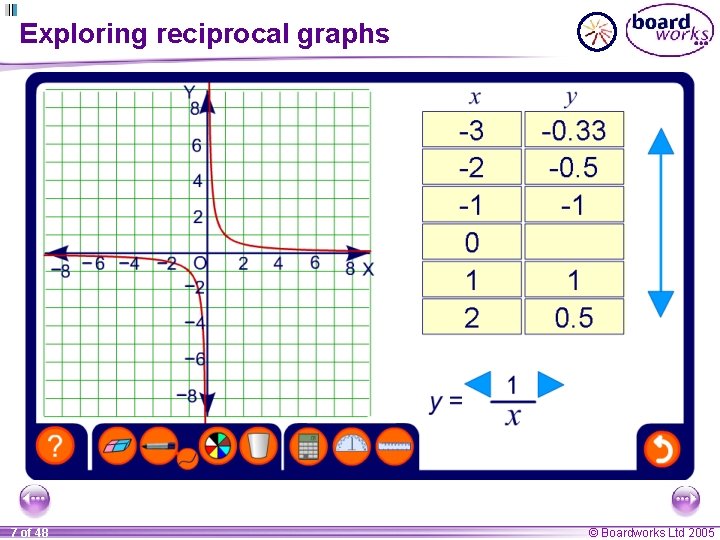
Reciprocal functions A reciprocal function always contains a fraction with a term in x in the denominator. Here are examples of three simple reciprocal functions: 3 y= x 1 y= x – 4 y= x In each of these examples the axes form asymptotes. The curve never touches these lines. 6 of 48 © Boardworks Ltd 2005

Exploring reciprocal graphs 7 of 48 © Boardworks Ltd 2005

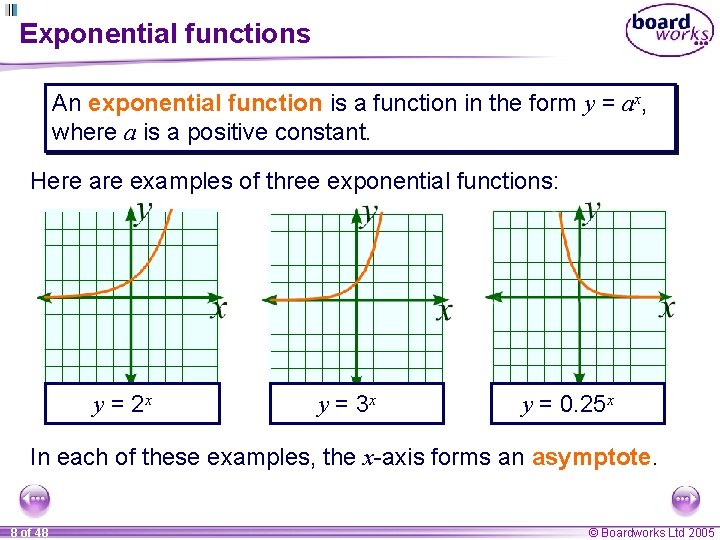
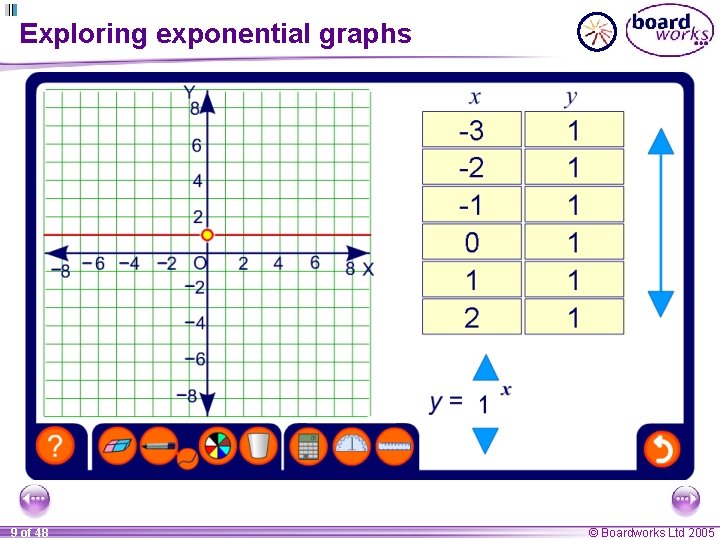
Exponential functions An exponential function is a function in the form y = ax, where a is a positive constant. Here are examples of three exponential functions: y = 2 x y = 3 x y = 0. 25 x In each of these examples, the x-axis forms an asymptote. 8 of 48 © Boardworks Ltd 2005

Exploring exponential graphs 9 of 48 © Boardworks Ltd 2005

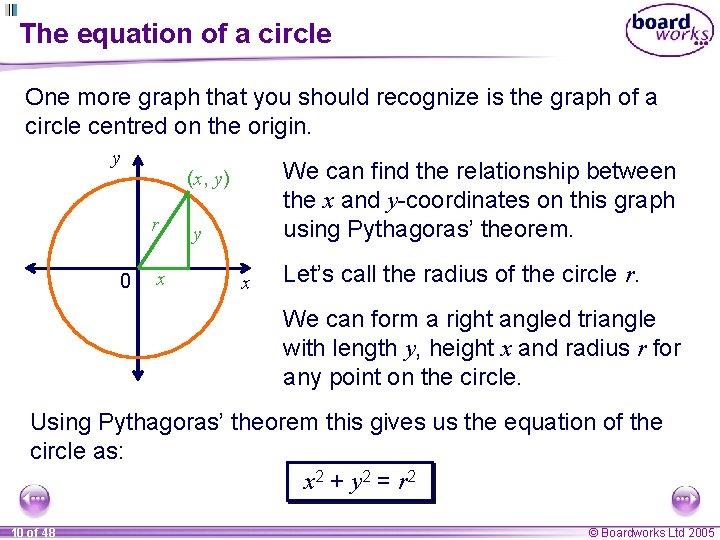
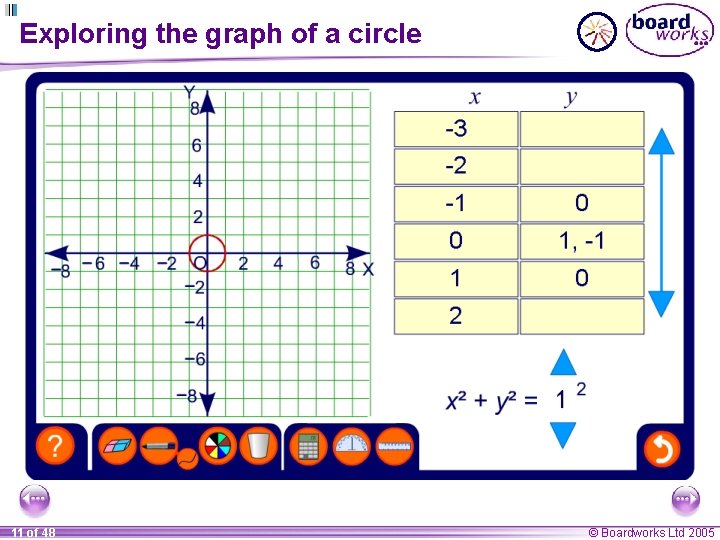
The equation of a circle One more graph that you should recognize is the graph of a circle centred on the origin. y r 0 We can find the relationship between the x and y-coordinates on this graph using Pythagoras’ theorem. (x, y) x y x Let’s call the radius of the circle r. We can form a right angled triangle with length y, height x and radius r for any point on the circle. Using Pythagoras’ theorem this gives us the equation of the circle as: x 2 + y 2 = r 2 10 of 48 © Boardworks Ltd 2005

Exploring the graph of a circle 11 of 48 © Boardworks Ltd 2005

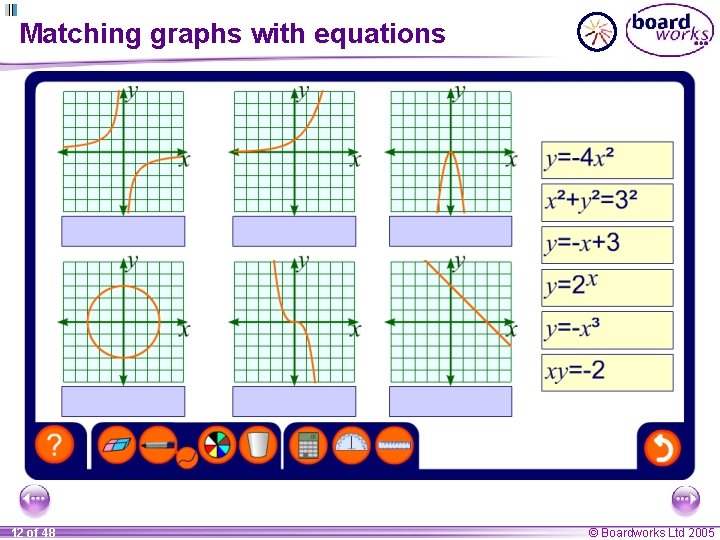
Matching graphs with equations 12 of 48 © Boardworks Ltd 2005

Contents A 9 Graphs of non-linear functions A A 9. 1 Plotting curved graphs A A 9. 2 Graphs of important non-linear functions A A 9. 3 Using graphs to solve equations A A 9. 4 Solving equations by trial and improvement A A 9. 5 Function notation A A 9. 6 Transforming graphs 13 of 48 © Boardworks Ltd 2005

Transforming graphs of functions Graphs can be transformed by translating, reflecting, stretching or rotating them. The equation of the transformed graph will be related to the equation of the original graph. When investigating transformations it is most useful to express functions using function notation. For example, suppose we wish to investigate transformations of the function f(x) = x 2. The equation of the graph of y = x 2, can be written as y = f(x). 14 of 48 © Boardworks Ltd 2005

Vertical translations Here is the graph of y = x 2, where y = f(x). This is the graph of y = f(x) + 1 y and this is the graph of y = f(x) + 4. What do you notice? This is the graph of y = f(x) – 3 x and this is the graph of y = f(x) – 7. What do you notice? The graph of y = f(x) + a is the graph of y = f(x) translated by the vector 0. a 15 of 48 © Boardworks Ltd 2005

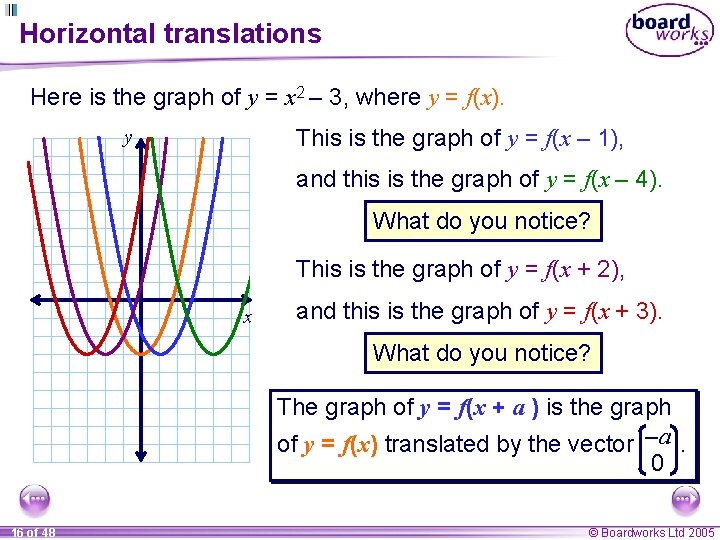
Horizontal translations Here is the graph of y = x 2 – 3, where y = f(x). This is the graph of y = f(x – 1), y and this is the graph of y = f(x – 4). What do you notice? This is the graph of y = f(x + 2), x and this is the graph of y = f(x + 3). What do you notice? The graph of y = f(x + a ) is the graph of y = f(x) translated by the vector –a. 0 16 of 48 © Boardworks Ltd 2005

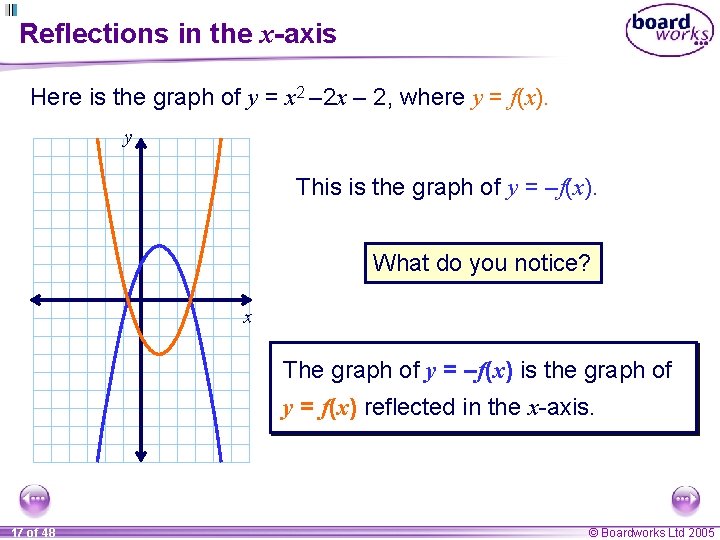
Reflections in the x-axis Here is the graph of y = x 2 – 2 x – 2, where y = f(x). y This is the graph of y = –f(x). What do you notice? x The graph of y = –f(x) is the graph of y = f(x) reflected in the x-axis. 17 of 48 © Boardworks Ltd 2005

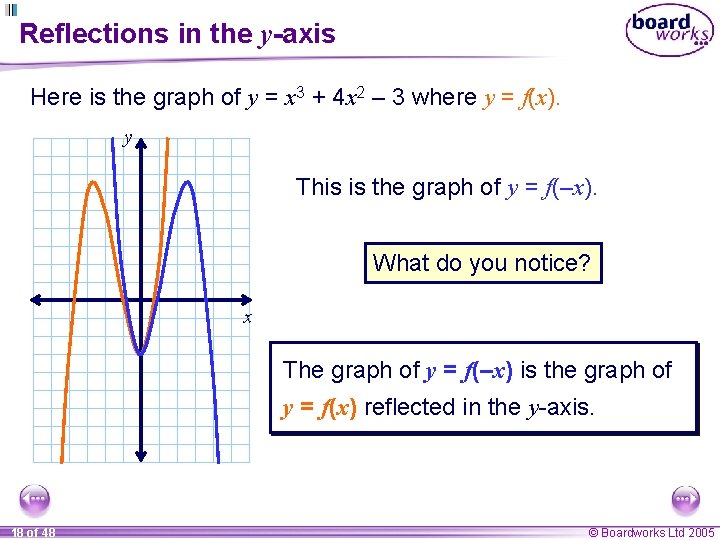
Reflections in the y-axis Here is the graph of y = x 3 + 4 x 2 – 3 where y = f(x). y This is the graph of y = f(–x). What do you notice? x The graph of y = f(–x) is the graph of y = f(x) reflected in the y-axis. 18 of 48 © Boardworks Ltd 2005

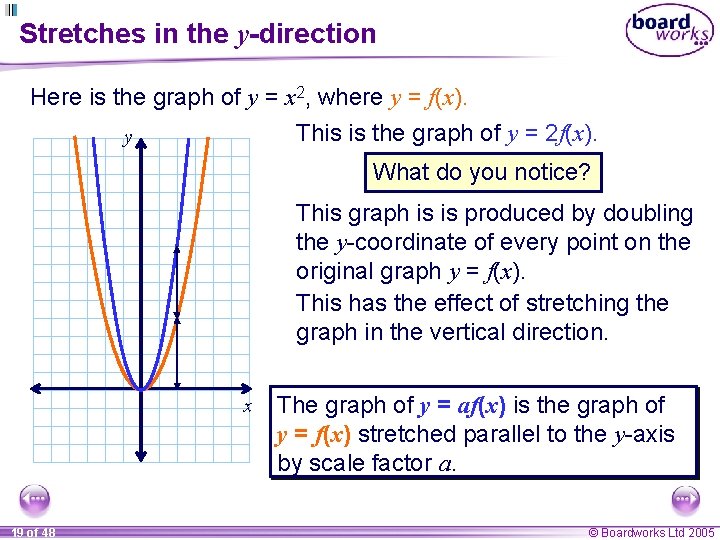
Stretches in the y-direction Here is the graph of y = x 2, where y = f(x). This is the graph of y = 2 f(x). y What do you notice? This graph is is produced by doubling the y-coordinate of every point on the original graph y = f(x). This has the effect of stretching the graph in the vertical direction. x 19 of 48 The graph of y = af(x) is the graph of y = f(x) stretched parallel to the y-axis by scale factor a. © Boardworks Ltd 2005

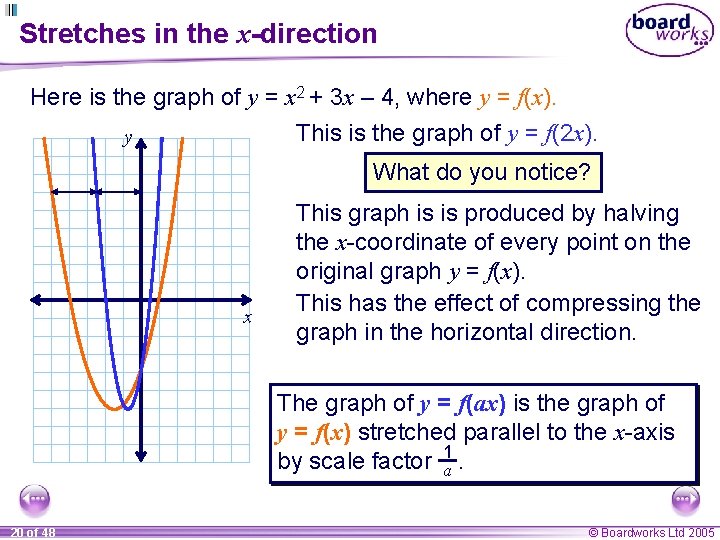
Stretches in the x-direction Here is the graph of y = x 2 + 3 x – 4, where y = f(x). This is the graph of y = f(2 x). y What do you notice? x This graph is is produced by halving the x-coordinate of every point on the original graph y = f(x). This has the effect of compressing the graph in the horizontal direction. The graph of y = f(ax) is the graph of y = f(x) stretched parallel to the x-axis by scale factor 1 a. 20 of 48 © Boardworks Ltd 2005

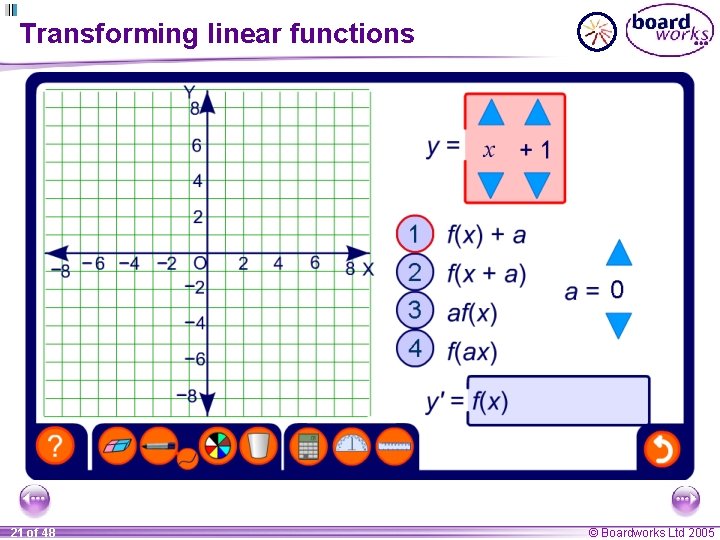
Transforming linear functions 21 of 48 © Boardworks Ltd 2005

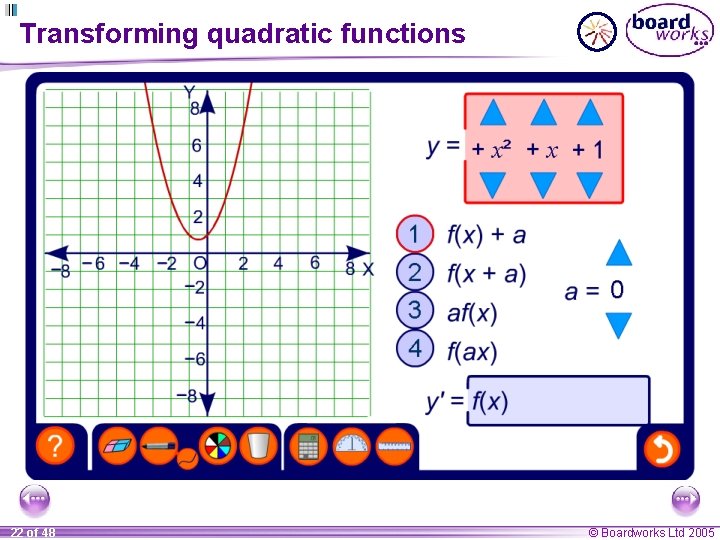
Transforming quadratic functions 22 of 48 © Boardworks Ltd 2005

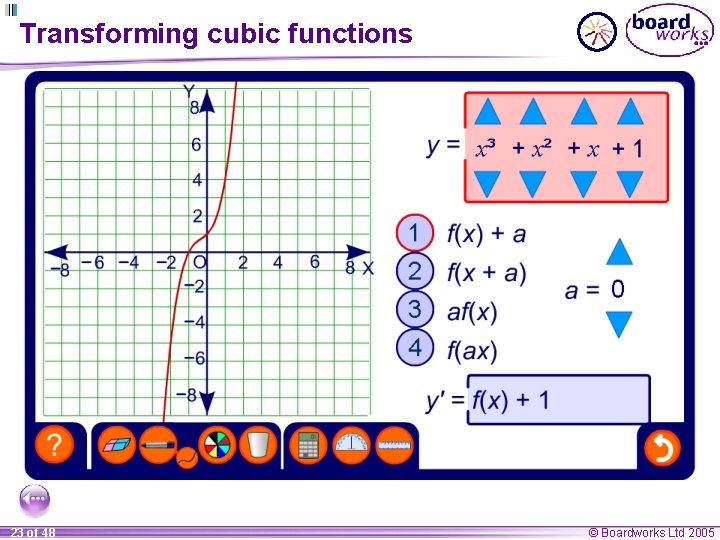
Transforming cubic functions 23 of 48 © Boardworks Ltd 2005
 End behavior chart
End behavior chart Nonlinear table
Nonlinear table State testing and testability tips
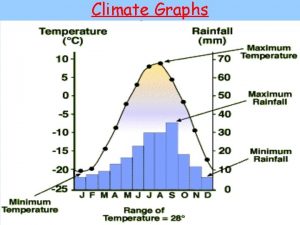
State testing and testability tips Graphs that compare distance and time are called
Graphs that compare distance and time are called Graphs that enlighten and graphs that deceive
Graphs that enlighten and graphs that deceive Patterns and nonlinear functions
Patterns and nonlinear functions Algebra graphs and functions
Algebra graphs and functions Unit 5 polynomial functions
Unit 5 polynomial functions 6-7 investigating graphs of polynomial functions
6-7 investigating graphs of polynomial functions Analyzing graphs of polynomial functions calculator
Analyzing graphs of polynomial functions calculator Linear polynomial
Linear polynomial 6-7 investigating graphs of polynomial functions
6-7 investigating graphs of polynomial functions Elementary functions graphs
Elementary functions graphs 5-4 practice analyzing graphs of polynomial functions
5-4 practice analyzing graphs of polynomial functions Investigating graphs of polynomial functions
Investigating graphs of polynomial functions Chapter 2 functions and their graphs answers
Chapter 2 functions and their graphs answers Lesson 4-2 practice a inverses of relations and functions
Lesson 4-2 practice a inverses of relations and functions Domain of trig functions
Domain of trig functions 2-5 graphs of expense and revenue functions
2-5 graphs of expense and revenue functions Trigonometry graph
Trigonometry graph Lesson 3 rational functions and their graphs
Lesson 3 rational functions and their graphs Chapter 2 functions and graphs
Chapter 2 functions and graphs Common functions and their graphs
Common functions and their graphs Chapter 1 functions and their graphs
Chapter 1 functions and their graphs