Computer Representation of Information CSCE 106 Outline n

Computer Representation of Information CSCE 106

Outline n Representation of Characters n Mathematical operations on numbers (addition) n Signed integer representation Sign-magnitude notation u Two’s complement notation n Binary Notations Exercises n Real Numbers Representation u CSCE 106 2

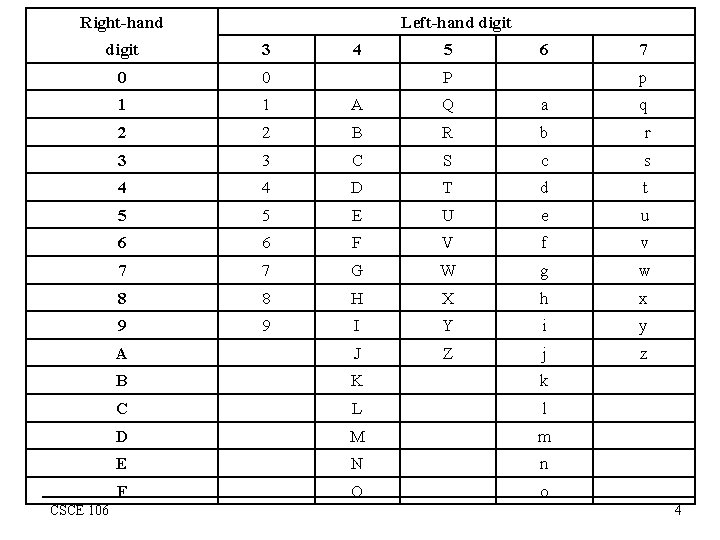
Representation of Characters n n n A unique binary pattern/value is used to represent each of the printable characters on your keyboard (e. g. A, a, 4, *, [, ’, etc. …), as well as the special control/unprintable characters (e. g. carriage return, line feed, tab, space, etc. …). A byte (8 bits) gives you the opportunity to have 28 (256) unique representations/patterns/values. There are standard character coding schemes to ease interchange of information, e. g. ASCII. The code is designed in such a way not only to preserve uniqueness, but also to keep the order which is often needed in manipulating characters/text, e. g. sorting. The value/pattern used to represent “A” is less by one than the value used to represent “B”, … etc. CSCE 106 3

Right-hand Left-hand digit 3 0 0 1 1 A Q a q 2 2 B R b r 3 3 C S c s 4 4 D T d t 5 5 E U e u 6 6 F V f v 7 7 G W g w 8 8 H X h x 9 9 I Y i y A J Z j z B K k C L l D M m E N n F O o CSCE 106 4 5 6 P 7 p 4

Mathematical Operations on Numbers (Addition) Most of the mathematical operations on numbers from different number systems are conceptually identical to the decimal arithmetic you are used to. n To add two numbers you do the following: Start at the rightmost digit. While there are more digits: Add the current digit of each operand. If the sum is less than the base/radix then record that sum, otherwise record the difference between the sum and the base/radix, and add one to the next digit of operand 1. n CSCE 106 5

Mathematical Operations on Numbers (Addition) (cont’d) Decimal numbers: 1610 + 1510 -----3110 Start by adding 6 + 5. The sum (11) is not less than the base (10), so (11 -10) record 1, and carry 1 by adding it to the first digit of 16, giving 2, then add the next digit from each operand (2+1) to give 3. u Octal numbers: 168 + 158 -----338 Start by adding 6 + 5. The sum (1110) is not less than the base (8), so (11 -8) record 3, and carry 1 by adding it to the first digit of 16, giving 2, then add the next digit from each operand (2+1) to give 3. The above discussions can be generalized to any base. u n CSCE 106 6

Signed Integers n n So far, we were representing unsigned integers in binary. We need to have a way for representing the sign of the number (positive or negative). We need to have a sign bit, or figure out some other way, so as to be able to represent negative values as well as positive ones. We will study two notations for representing signed integers: u sign-magnitude notation, and u two’s complement notation. CSCE 106 7

Sign-Magnitude Notation n n It leaves the left most bit for the sign (sign bit), and uses the rest of the bits (m - 1) to represent the integer. 0 in the sign bit is used to represent positive values, and 1 is used to represent negative values. Therefore, the range of integer values i which can be represented with m bits is: -(2 m-1 – 1) <= i <= +(2 m-1 – 1) Using the sign–magnitude notation (in a byte): u +2910 is represented as 0001 1101 u -2910 is represented as 1001 1101 CSCE 106 8

Problems with Sign-Magnitude Notation n You might find this technique simple, natural, and straight forward, as it closely resembles the way you are used to writing numbers. n However this notation creates mainly two problems for the computers: 1. 0 representation (0000 is not 10000000). 2. Addition of mixed sign numbers (10000101 (– 510) and 00000001 doesn’t result in – 4). n Thus the sign-magnitude notation is not used in computers. CSCE 106 9

Two’s Complement Notation Two’s complement of an m-bit number N = (Bitwise/one’s complement of N) + 1 n Examples of 8 -bit numbers and their 2’s complement representation: n +1 = 000000012 u – 1 = 11111110 + 1 = 1111 u +29 = 000111012 u – 29 = 11100010 + 1 = 11100011 (2’s complement of 111000112 = 000111002 + 1 = 000111012 (29)) u CSCE 106 10

Two’s Complement Notation (cont’d) n For an m-bit signed integer in two’s complement notation, the range of integer values is from – 2 m– 1 to 2 m– 1 – 1. When m = 8, the range is from – 128 to 127. u When m = 16, the range is from – 32768 to 32767. u n Two’s complement notation overcomes the problems of sign-magnitude notation. We have only one representation for the 0. u Addition of mixed sign integers give correct results (with no need for extra logic). u CSCE 106 11

Binary Notations Exercises Representations of integers in a byte (8 bits) using different binary notations: Integer 34 -23 -128 310 CSCE 106 Unsigned 00102 Not Possible Sign-magnitude 2's-complement 00102 100101112 Not Possible 00102 111010012 100000002 Not Possible 12

Exercises (cont’d) Add (-37) to (25) using 8 -bit two’s complement representation. 11 11 Carry Ans: 000110012 2510 11011011 2 -37 + + 10 ---------111101002 -1210 n CSCE 106 13

Exercises (cont’d) Subtract (39) from (-17) using 8 -bit two’s complement representation. 1111111 Carry Ans: 111011112 -1710 11011001 2 39 + 10 ---------110010002 -5610 n Final carry overflows 8 bits. CSCE 106 14

Real Numbers Representation n 101 100 10 -1 10 -2 10 -3 2 2. 6 2 5 decimal point Real or Floating-Point Numbers, e. g. 22. 625 n 24 23 22 21 20 2 -1 2 -2 2 -3 1 0 1 1 0 1 In binary point CSCE 106 15

Real Numbers Representation (cont’d) n Scientific notation: 2. 2625 x 101 exponent mantissa n Binary scientific notation: 1. 0110101 x 24 exponent mantissa n Hence it consists of a sign bit, a mantissa field, and an exponent field. CSCE 106 16

Next lecture will be about Problem Solving Methods CSCE 106 17