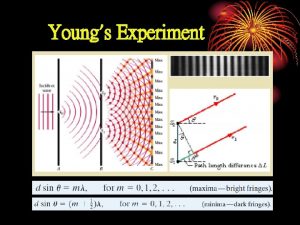
Coherent Communication of Classical Messages Aram Harrow MIT

Coherent Communication of Classical Messages Aram Harrow (MIT) quant-ph/0307091

outline • What is coherent communication? • Why should you care about it? • Where can you obtain it? • How can you use it?

beyond qubits and cbits Let {|xi}x=0, 1 be a basis for C 2. • qubit: |xi. A!|xi. B • cbit: |xi. A!|xi. B|xi. E • coherent bit (cobit): |xi. A!|xi. A|xi. B • ebit: |Fi=2 -1/2åx|xi. A|xi. B 1 qubit > 1 cobit > 1 cbit 1 qubit > 1 cobit > 1 ebit

motivation

cobit: |xi. A!|xi. A|xi. B motivation #1 irreversibility in q. info. theory 1 qubit > 1 ebit and 1 qubit > 1 cbit are both individually optimal, but the best way to generate qubits is 2 cbits + 1 ebit ¸ 1 qubit. Super-dense coding and teleportation appear to be dual, but composing them wastes entanglement. Claim: Irreversibility comes from the transformation “ 1 cobit > 1 cbit. ”

cobit: |xi. A!|xi. A|xi. B motivation #2 communication with unitary gates Suppose Alice can send Bob n cbits using a unitary interaction (i. e. U|xi. A|0 i. B ¼ |xi. B|yxi. AB for x 2{0, 1}n). This must be more powerful than an arbitrary noisy interaction, because it implies the ability to create n ebits. But what exactly is its power? Claim: Unitary interactions send cobits while general interactions send cbits.

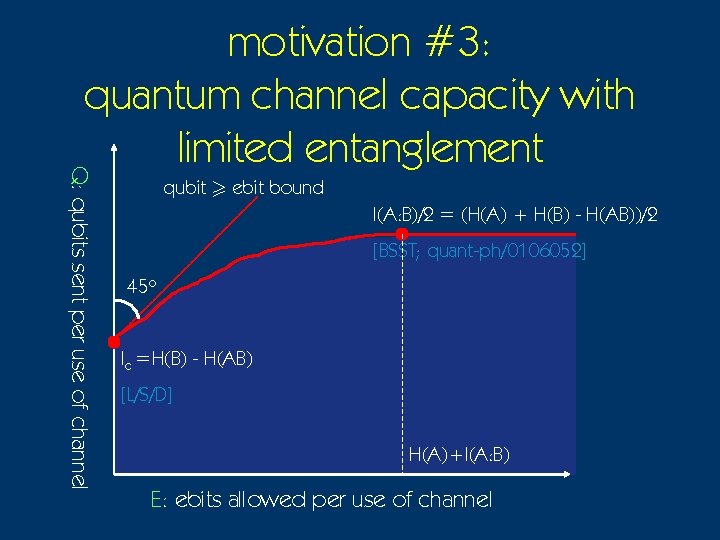
Q: qubits sent per use of channel motivation #3: quantum channel capacity with limited entanglement qubit > ebit bound I(A: B)/2 = (H(A) + H(B) - H(AB))/2 [BSST; quant-ph/0106052] 45 o Ic =H(B) - H(AB) [L/S/D] H(A)+I(A: B) E: ebits allowed per use of channel

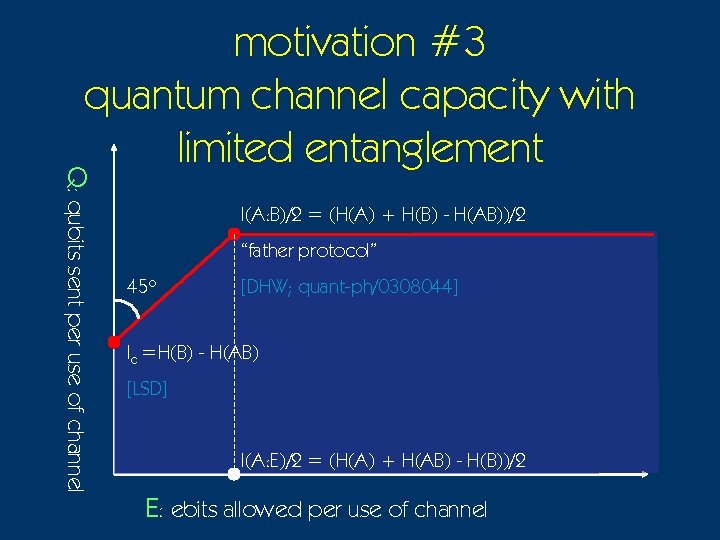
Q: qubits sent per use of channel motivation #3 quantum channel capacity with limited entanglement I(A: B)/2 = (H(A) + H(B) - H(AB))/2 “father protocol” 45 o [DHW; quant-ph/0308044] Ic =H(B) - H(AB) [LSD] I(A: E)/2 = (H(A) + H(AB) - H(B))/2 E: ebits allowed per use of channel

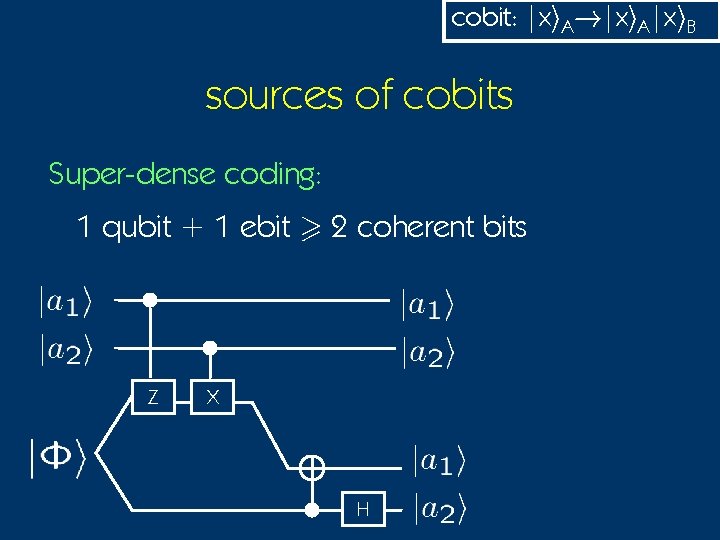
cobit: |xi. A!|xi. A|xi. B sources of cobits Super-dense coding: 1 qubit + 1 ebit > 2 coherent bits Z X H

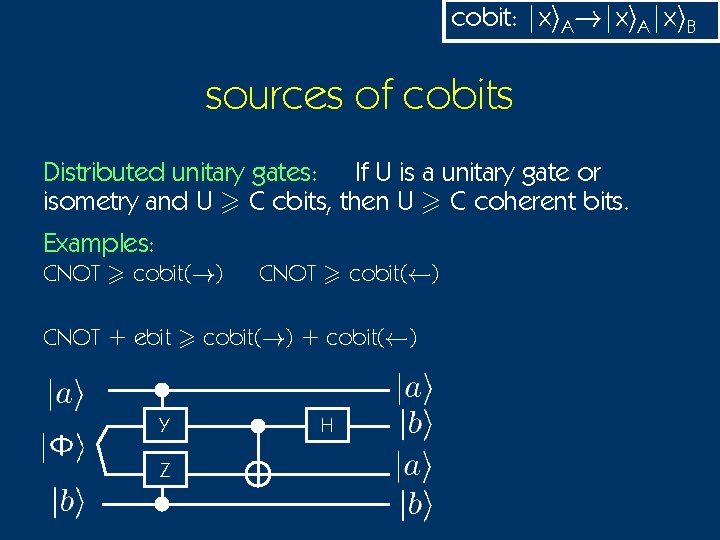
cobit: |xi. A!|xi. A|xi. B sources of cobits Distributed unitary gates: If U is a unitary gate or isometry and U > C cbits, then U > C coherent bits. Examples: CNOT > cobit(!) CNOT > cobit(Ã) CNOT + ebit > cobit(!) + cobit(Ã) Y Z H

cobit: |xi. A!|xi. A|xi. B noisy sources of cobits [Devetak, Harrow, Winter; quant-ph/0308044] General rule: If N can send a classical message that is nearly independent of the residual state (of Alice, Bob and environment), then that message can be made coherent. Example: entanglement-assisted classical capacity [BSST] N + H(A) ebits > I(A: B) cbits Ux N D The environment always sees a maximally mixed state! N + H(A) ebits > I(A: B) cobits ¼|xi. B|yxi. BE

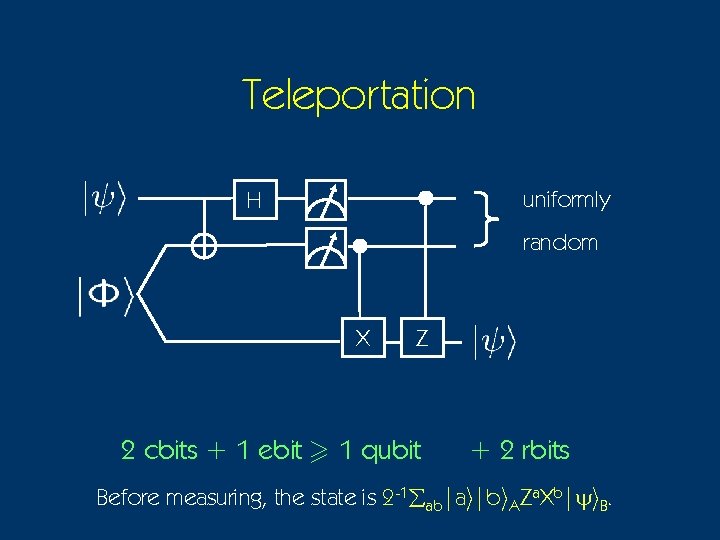
Teleportation uniformly H random X Z 2 cbits + 1 ebit > 1 qubit + 2 rbits Before measuring, the state is 2 -1åab|ai|bi. AZa. Xb|yi. B.

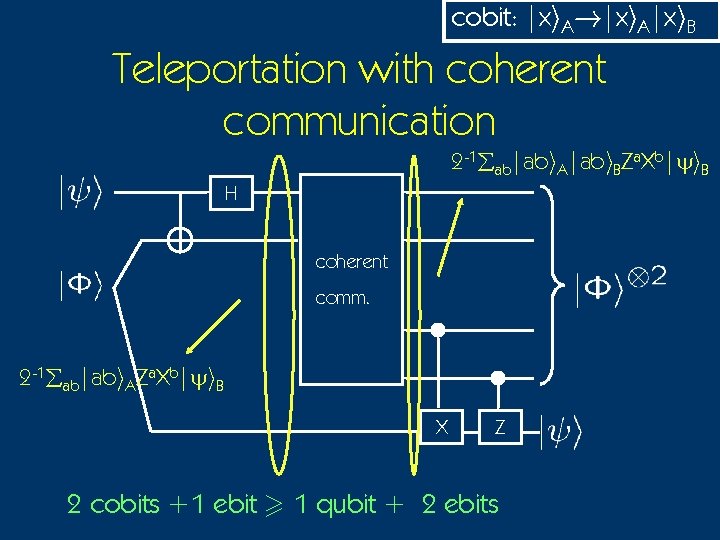
cobit: |xi. A!|xi. A|xi. B Teleportation with coherent communication 2 -1åab|abi. A|abi. BZa. Xb|yi. B H coherent comm. 2 -1åab|abi. AZa. Xb|yi. B X Z 2 cobits +1 ebit > 1 qubit + 2 ebits

cobit: |xi. A!|xi. A|xi. B Simple consequences • 2 coherent bits = 1 qubit + 1 ebit (C) (using entanglement catalytically) • Teleportation and super-dense coding are no longer irreversible. • N + H(A) ebits > I(A: B) cobits = I(A: B)/2 (qubit + ebit) H(A) - I(A: B)/2 = (H(A) + H(E) - H(B))/2 = I(A: E)/2 father: N + I(A: E)/2 ebits > I(A: B)/2 qubits

cobit: |xi. A!|xi. A|xi. B general rule for using cobits Simultaneous communication and entanglement generation Suppose X + C cbits > Y and the classical message sent is independent of the output state. Then X + C coherent bits > Y + C ebits

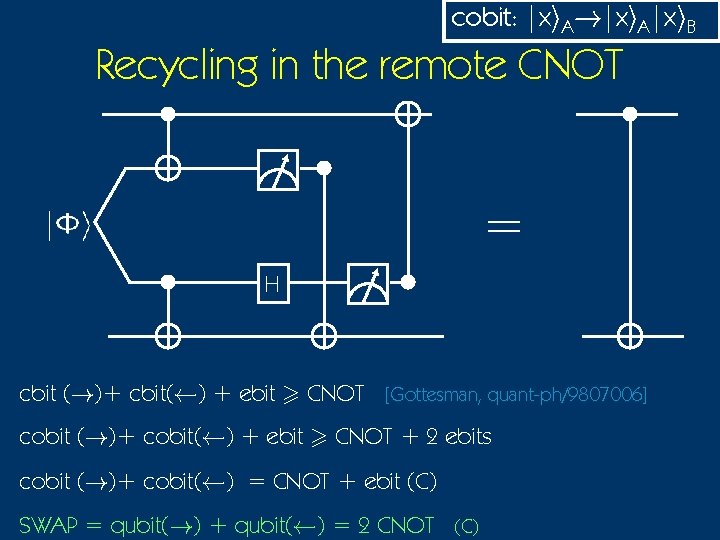
cobit: |xi. A!|xi. A|xi. B Recycling in the remote CNOT = H cbit (!)+ cbit(Ã) + ebit > CNOT [Gottesman, quant-ph/9807006] cobit (!)+ cobit(Ã) + ebit > CNOT + 2 ebits cobit (!)+ cobit(Ã) = CNOT + ebit (C) SWAP = qubit(!) + qubit(Ã) = 2 CNOT (C)

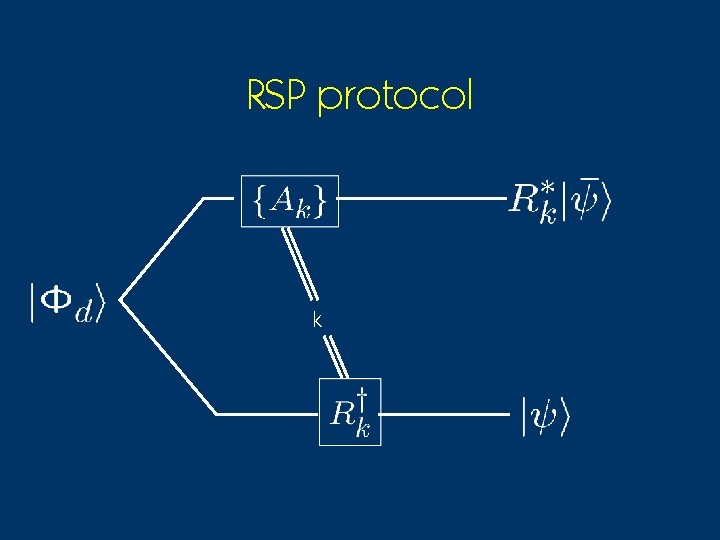
Remote State Preparation 1 cbit + 1 ebit > 1 remote qubit (A) Given |Fdi and a description of |yi 2 Cd, Alice can prepare |yi in Bob’s lab with error e by sending him log d + O(log d)/e 2) cbits. [Bennett, Hayden, Leung, Shor and Winter, quant-ph/0307100]

RSP protocol k

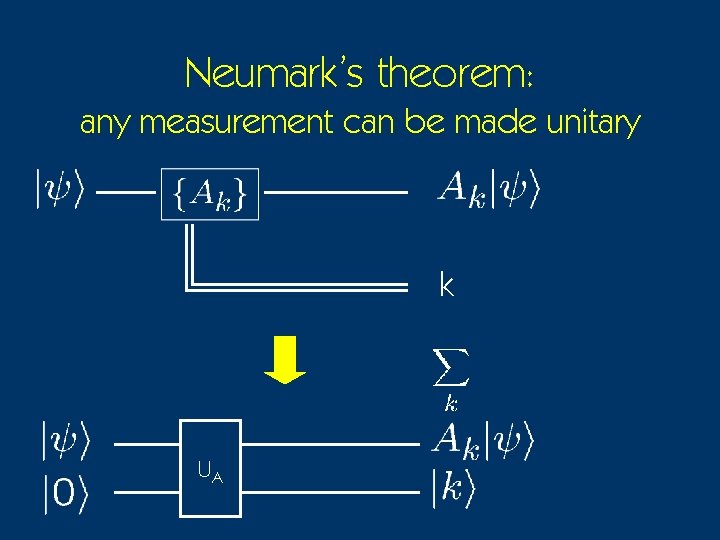
Neumark’s theorem: any measurement can be made unitary k UA

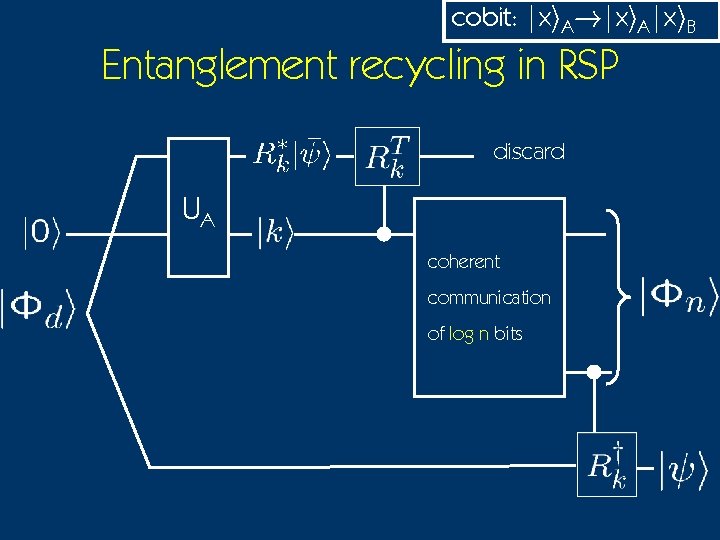
cobit: |xi. A!|xi. A|xi. B Entanglement recycling in RSP discard UA coherent communication of log n bits

cobit: |xi. A!|xi. A|xi. B Coherent RSP 1 cobit + 1 ebit > 1 remote qubit + 1 ebit 1 cobit > 1 remote qubit (C) Corollary 1: Super-dense coding of quantum states 1 qubit + 1 ebit > 2 remote qubits (C) (Independent direct proof in [Harrow, Hayden, Leung; quant-ph/0307221]. ) Corollary 2: The remote state capacity of a unitary gate equals its classical capacity.

RSP of entangled states (e. RSP) Let E={pi, |yii. AB} be an ensemble of bipartite pure states. Define S(E)=S(åipi. Tr. Ayi), E(E)=åipi. S(Tr. Ayi), c(E)=S(E)-E(E). e. RSP: c(E) cbits + S(E) ebits > E (A) [BHLSW] make it coherent: c(E) cobits + E(E) ebits > E (A)

Unitary gate capacities Define Ce to be the forward classical capacity of U assisted by e ebits of entanglement per use, so that 1 use of U + e ebits > Ce cbits (A) Solution: Ce=sup. E {c(UE) - c(E) : E(E) - E(UE)6 e} (In [BHLS; quant-ph/0205057], this was proved for e=1. )

Warmup: entanglement capacity Define E(U) to be the largest number satisfying U > E(U) ebits (A). Claim: E(U) = sup|yi E(U|yi) – E(|yi) Proof: [BHLS; quant-ph/0205057] |yi + U > U|yi > E(U|yi) ebits (concentration) >|yi + E(U|yi)-E(|yi) ebits (dilution) Thus: U > E(U|yi)-E(|yi) ebits (A)

Coherent HSW coding Lemma: Let E={pi, yi} be an ensemble of bipartite pure states that Alice can prepare in superposition. Then E > c(E) cobits + E(E) ebits (A) Proof: Choose a good code on E n. Bob’s measurement obtains ¼nc(E) bits of Alice’s message and determines the codeword with high probability, causing little disturbance. Thus, this measurement can be made coherent. Since Alice and Bob know the codeword, they can then do entanglement concentration to get ¼n. E(E) ebits.

Protocol achieving Ce E + U > UE > c(UE) cobits + E(UE) ebits (coherent HSW) > E + (c(UE)-c(E)) cobits + (E(UE)-E(E)) ebits (coherent RSP) Thus, U + (E(E)-E(UE)) ebits > (c(UE)-c(E)) cobits (A)

Quantum capacities of unitary gates Define Qe(U) to be the largest number satisfying U + e ebits > Qe qubits. Using 2 cobits = 1 qubit + 1 ebit, we find

References A. W. Harrow. “Coherent Communication of Classical Messages” quant-ph/0307091 I. Devetak, A. W. Harrow and A. Winter. “A family of quantum protocols. ” quant-ph/0308044

Conclusions • Whenever a classical message is independent of the residual Alice-Bob-environment state, it can be made coherent. • 2 coherent bits = 1 qubit + 1 ebit • consequences include: super-dense coding of [entangled] quantum states, SWAP=2 CNOT, classical and quantum capacities of unitary gates, tradeoff curves for quantum channel capacities and the asymptotic equivalence of ensembles of bipartite pure states.