Classical Statistical Mechanics 1 dimensional Simple Harmonic Oscillator














- Slides: 15

Classical Statistical Mechanics: 1 dimensional Simple Harmonic Oscillator

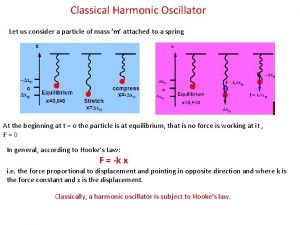
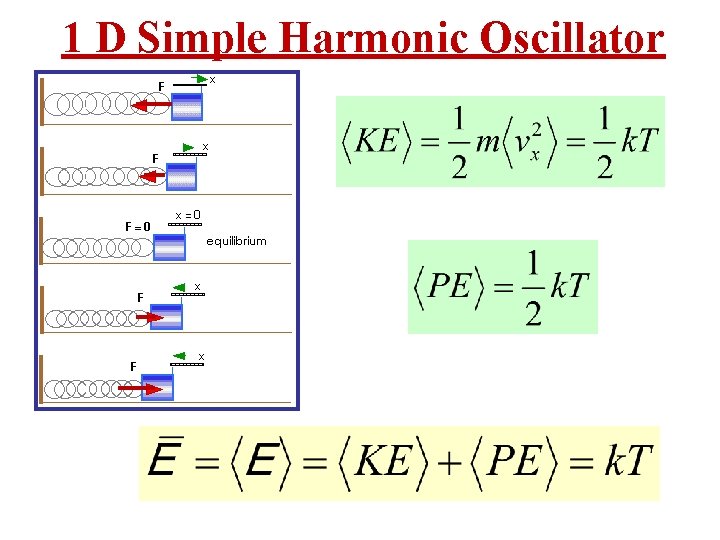
Recall the Equipartition Theorem: • In the Classical Cannonical Ensemble it is easy to show that The thermal average energy of a particle per independent degree of freedom is (½)k. BT.

The Boltzmann Distribution Canonical Probability Function P(E): • This is defined so that P(E)d. E probability to find a particular molecule between E & E + d. E Z Define: The Energy Distribution Function (Number Density) n. V(E): • This is defined so that n. V(E)d. E number of molecules per unit volume with energy between E & E + d. E

Examples: Equipartition of Energy in Classical Statistical Mechanics Free Particle Z

Other Examples of the Equipartion Theorem LC Circuit Harmonic Oscillator Free Particle in 3 D Rotating Rigid Body

1 D Simple Harmonic Oscillator

Quantum Statistical Mechanics: 1 dimensional Simple Harmonic Oscillator

Quantum Mechanical Simple Harmonic Oscillator • Quantum Mechanical results for a simple harmonic oscillator with classical frequency ω: n = 0, 1, 2, 3, . . The Energy is E quantized! Energy levels are equally spaced! ħω ħω ħω

Thermal Average Energy for a Quantum Simple Harmonic Oscillator • We just discussed the fact that the Quantized Energy solution to the Schrodinger Equation for a single oscillator is: ħω n = 0, 1, 2, 3, . . • Now, let this oscillator interact with a heat reservoir at absolute temperature T, & use the Canonical Ensemble to calculate thermal average energy: <E> or < >

Quantized Energy of a Single Oscillator: ħω n = 0, 1, 2, 3, . . • On interaction with a heat reservoir at T, & using the Canonical Ensemble, the probability Pn of the oscillator being in level n is proportional to: • In the Canonical Ensemble, the average energy of the harmonic oscillator of angular frequency ω at temperature T is:

• Now, straightforward but tedious math manipulation! • Thermal average energy: • Putting in the explicit form: Denominator = Partition Function Z.

Denominator = Partition Function Z. • Evaluate using Binomial expansion for x << 1:

ε can be rewritten: Final Result:

(1) This is the Thermal Average Energy for a Single One Dimensional Harmonic Oscillator. • The first term is called “The Zero-Point Energy”. • It’s physical interpretation is that, even at T = 0 K, the oscillator will vibrate & have a non-zero energy. The Zero Point Energy = minimum energy of the system.

Thermal Average Oscillator Energy: (1) • The first term in (1) is the Zero Point Energy. • The denominator of second term in (1) is often written: (2) • (2) is interpreted as thermal average of quantum number n at temperature T & frequency ω. • In modern terminology, (2) is called The Bose-Einstein Distribution: or The Planck Distribution.
 Wave function of quantum harmonic oscillator
Wave function of quantum harmonic oscillator Mechanical energy
Mechanical energy Selection rules for harmonic oscillator
Selection rules for harmonic oscillator Selection rule for anharmonic oscillator
Selection rule for anharmonic oscillator Simple harmonic oscillator amplitude
Simple harmonic oscillator amplitude 戴明鳳
戴明鳳 Simple harmonic oscillator
Simple harmonic oscillator Simple definition of motion
Simple definition of motion Maximum speed of simple harmonic oscillator
Maximum speed of simple harmonic oscillator Wave function of quantum harmonic oscillator
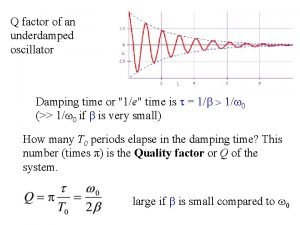
Wave function of quantum harmonic oscillator Q factor damped harmonic oscillator
Q factor damped harmonic oscillator Relaxation time of damped harmonic oscillator
Relaxation time of damped harmonic oscillator Harmonic oscillator propagator
Harmonic oscillator propagator Harmonic oscillator spring
Harmonic oscillator spring Zero point energy formula
Zero point energy formula First harmonic and second harmonic
First harmonic and second harmonic