Chemical Thermodynamics Third Law of Thermodynamics Prof Dr



















- Slides: 19

Chemical Thermodynamics Third Law of Thermodynamics Prof. Dr. Samih A. Halawy

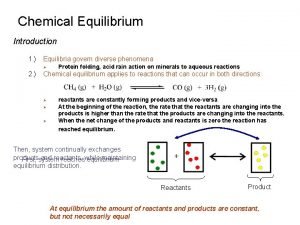
Third Law of Thermodynamics n n n Another fundamental principle of thermodynamics which deals with the entropy of pure crystalline substance at the absolute zero of temperature, has come into being, the principle called the third law of thermodynamics, states that: the entropy of all pure crystalline solids may be taken as zero at the absolute zero of temperature. The statement is confined to pure crystalline solids because theoretical argument and experimental evidence have shown that the entropy of solutions and super cooled liquids is not zero at 0 K.

n n n The importance of the third law lies in the fact that it permits the calculation of absolute values of the entropy of pure substances at any temperature, provided its heat capacity is known from 0 K to the temperature in question and that all heats of transition, with the corresponding temperature, are known. Since, however, according to the third law S = 0 for a pure crystalline substance at T = 0. Hence : -

Third Law of Thermodynamics The entropy of a pure crystalline substance at absolute zero is 0.

Standard Entropies These are molar entropy values of substances in their standard states. n Standard entropies tend to increase with increasing molar mass. n

Standard Entropies Larger and more complex molecules have greater entropies.

n n The total absolute entropy of a substance in a particular state at a given temperature will be the sum of all entropy changes the substance has to undergo in order to reach the particular state from the crystalline solid at absolute zero. Thus, if a substance is gaseous at 1 atm. pressure and 25 C, the entropy of the gas must be the sum of the entropies involved in : (a) Heating the crystalline solid from T = 0 to T = Tf , the fusion point. (b) The entropy of fusion, Hf/T. (c) The entropy of heating the liquid from Tf to Tb, the normal boiling point.

n n (d) The entropy of vaporization Hv/T and, (e) The entropy of heating the gas from Tb to 298 K. These changes can be represented as follows: - It follows, therefore, that the absolute entropy of any substance at a temperature T may be rewritten as: -

The Free Energy • All changes in nature are due to the tendency on the part of the systems to reach a condition of maximum stability, i. e. equilibrium. Once, equilibrium has been reached, the system is stable. • From a system in equilibrium no work can be obtained, but a system on the way to equilibrium may be made to yield useful work. • A system undergoing change can perform maximum work only when change is carried out reversibly. • If the process is more or less irreversible, i. e. , naturally occurring process, the amount of work obtained is always below the maximum.

• Hence, for a process taking place at constant temperature and pressure and involving volume change from V 1 to V 2, the work done against the atmosphere is • W= P(V 2 -V 1)= P V • These are work and free energy functions represented by A and F (or G) respectively. The work function: • The work function (A) is defined by : - A = E –TS Where E is the energy content of the system, T is the absolute temperature and S its entropy.

Since E, T and S depend upon thermodynamic state of the system only and not on its previous history, it is evident that the function (A) is also a single valued function of the state of the system. Consider an isothermal change at temperature T from the initial state indicated by subscript-1 to the final state indicated by sbscript-2, so that A 1 = E 1 – TS 1 (1) A 2 = E 2 – TS 2 (2) Subtracting (1) from (2), we have : A 2 – A 1 = (E 2 – E 1) – T (S 2 – S 1) • or A = E – T S (3)

• Where A is the increase in function A, E is the corresponding increase in internal energy and S is the increase in the entropy of the system. • Since S =Q/T , where Q is the heat taken up when the change is carried out in a reversible manner at a constant temperature, we have : • A = E – Q (4) • According to the first law of thermodynamics, • E = (Q – W), or – W = E – Q (5) • Substituting this value in equation (4), we get - A = W (6) i. e. , the decrease in the work function A in any process at constant temperature gives the maximum work

That can be obtained from the system during any change. Free Energy Function: The free energy function (F) is defined by : G = H – TS Where H is the heat content of the system, T is its temperature and S its entropy. Like work function (A), the free energy (G) is also a single valued function of thermodynamic state of the system and is an extensive property. If at a constant temperature T, the system undergoes a change from a state 1 to state 2, so that G 1, H 1 and S represent thermodynamic functions of

the system in the initial state and G 2, H 2 and S 2 represent them in the final state, we have : G 1 = H 1 – TS 1 and G 2 = H 2 – TS 2 or (G 2 - G 1) = (H 2 – H 1) – T (S 2 – S 1) or G = H – T S (7) But H = E + P. V Therefore, G = E + P. V – T S (8) Since, ( E – T S) = A, and A = - W G = A + P. V or G = -W + P. V, or – G = W –P. V (9) But P. V represents the work done due to expansion against a constant external pressure P. It is evident, therefore, that the decrease if free energy (- G) accompanying a process taking place at constant

temperature and pressure is equal to the maximum work obtainable from the system other than the work of expansion. This quantity is referred to as the net work, so that Net Work = W – P. V = - G This quantity is of great importance in physical chemistry because the change in free energy is a measure of the net work witch may be electrical, chemical or surface work. In case of chemical reactions : A + B C + D , G = - (spontaneous) A + B C + D , G = + (non spontaneous) A + B C + D , G = 0 (equilibrium).

Examples: • The value of G for the reaction : • Ag. Cl (s) = Ag+ (a=1) + Cl- (a=1) is + 13. 304 cal. • Therefore if solid silver chloride is placed in contact with a solution containing silver and chloride ions at one molal activities, the reaction will proceed in the reverse of the way it is written and silver chloride will be precipitated. • On the other hand, the value of G change for the reaction : • Zn + 2 H+ (a=1) = Zn 2+ (a=1) + H 2 (a=1) • was found to be – 35. 18 cal. This minus sign shows the formation of H 2 gas.

• Free energy change in a chemical reaction: • The free energy change in a chemical reaction is calculated in the same manner as the entropy change and the change in enthalpy. • The procedure is represented by the equation: - • Example 1: • Calculate the value of G° for the combustion of ethane at 25°C. • C 2 H 6 (g) + 3. 5 O 2 (g) → 2 CO 2 (g) + 3 H 2 O (l)

If G° for CO 2, H 2 O, O 2, C 2 H 6 are – 94. 26, - 56. 69, 0, -7. 86 cal. G° 2 G°(CO 2) + 3 G°(H 2 O) – 3. 5 G°(O 2) - G°(C 2 H 6) n G° = (2 x -94. 26) + (3 x -56. 69) – 0 – (-7. 86) G° = - 350. 73 cal. n Example 2: - n Calculate the value of G° at 25°C for the reaction: - n n n Zn + 2 H+ = Zn 2+ + H 2 This reaction is somewhat usual, as three of the substances, H+, Zn and H 2, all have standard free energy of zero, Hence G° = G° (Zn 2+) + G° (H 2) - G° (Zn) – 2 G° (H+) G° = - 35. 18 + 0 – 0 = - 35. 18 cal.

Good Luck, see you next year in the higher level
 Newton's first law and second law and third law
Newton's first law and second law and third law Newton's first law of motion
Newton's first law of motion Third law of thermodynamics is depend on
Third law of thermodynamics is depend on Newton's third law of thermodynamics
Newton's third law of thermodynamics Third law of thermodynamics
Third law of thermodynamics Studyja
Studyja Gingival third vs cervical third
Gingival third vs cervical third Mount classification of dental caries
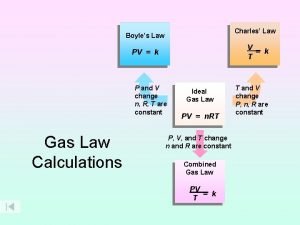
Mount classification of dental caries Boyle's law charles law avogadro's law
Boyle's law charles law avogadro's law Boyle's law charles law avogadro's law
Boyle's law charles law avogadro's law Reschual
Reschual Chemical engineering thermodynamics 8th solution chapter 3
Chemical engineering thermodynamics 8th solution chapter 3 Chemical engineering thermodynamics 8th solution chapter 4
Chemical engineering thermodynamics 8th solution chapter 4 Equilibrium thermodynamics
Equilibrium thermodynamics Chemical engineering thermodynamics 8th solution chapter 6
Chemical engineering thermodynamics 8th solution chapter 6 Thermodynamics chapter 2
Thermodynamics chapter 2 Chemical engineering thermodynamics 8th solution chapter 10
Chemical engineering thermodynamics 8th solution chapter 10 Thermodynamics for chemical engineering
Thermodynamics for chemical engineering First law of thermodynamics open system
First law of thermodynamics open system Thermodynamic
Thermodynamic