Chemical Thermodynamics Second Law of Thermodynamics Prof Dr








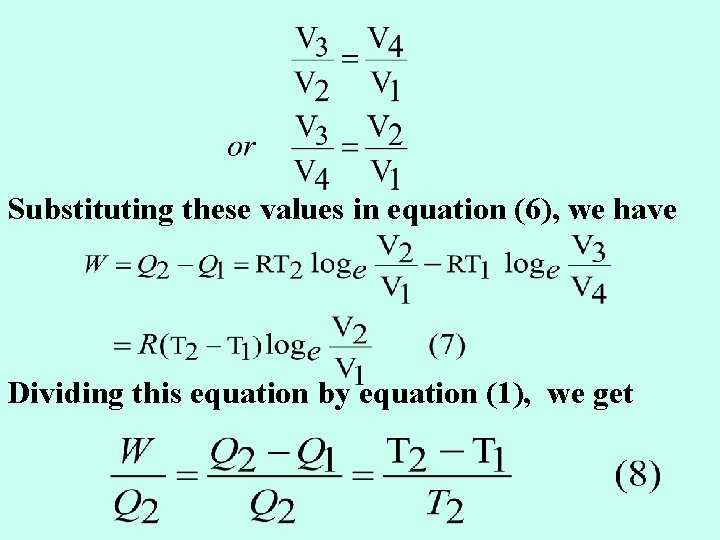

- Slides: 11

Chemical Thermodynamics Second Law of Thermodynamics Prof. Dr. Samih A. Halawy

The first law of Thermodynamics which is concerned with the equivalence of different forms of energy does not tell us anything about the ease of extent of convertibility of one form of energy into another. n When we come to examine the relationship between heat and work, we notice that whereas different forms of energy can be readily and completely converted into work. n

n n This limitation forms the basis of the second law of Thermodynamics which states that: "It is impossible to convert heat into an equivalent amount of work without producing other changes in some parts of the system. " The flow of heat being unidirectional from a higher to a lower temperature, another way of stating the law according to Claussius is: - n "It is impossible for a self acting machine, unaided by any external agency, to transfer heat from a body at a law to one at a higher temperature. "

The CARNOT CYCLE: n n To calculate the maximum extent to which heat can be converted into work, we make use of the Carnot Cycle which consists of a series of operations on a perfect gas so that at the conclusion of the operations, the gas is restored to its original state. Figure 1

First Operation – Isothermal Expansion n n Let one mole of a perfect gas be enclosed in a cylinder fitted with a frictionless piston and let its temperature, pressure and volume be T 2, P 1 and V 1 respectively. The cylinder is placed in contact with a heat reservoir whose temperature remains constant at T 2 Abs. Now let the gas expand isothermally and reversibly to the new volume V 2 (along AB in Fig. 1) taking in this process heat equal to Q 2 from the reservoir. Work W 1 done by the gas in this process according to a previous Eq. is : -

Second Operation – Adiabatic Expansion n The gas at B is now at a temperature T 2 and has a volume V 2 under the new pressure P 2. It is now completely isolated and allowed to expend adiabatically (along BC in Fig. 1) to the new volume V 3. Let the temperature drop to T 1. Here q = 0 and work W 2 is done at the expense of the internal energy of the gas.

Third operation – Isothermal Compression n n The cylinder is now placed in contact with a heat reservoir at T 1. The volume of the gas is V 3 and its pressure P 3. It is now isothermally and reversibly compressed until the volume is V 4. During this compression the gas gives out heat to the reservoir. Let its value be Q 1 so that he work done on the gas W 3 is: -

Fourth Operation – Adiabatic Compression n The gas with volume and temperature T 1 is again isolated and compressed adiabatically until it regains its original state i. e. its volume becomes V 1 and its temperature T 2. Work done W 4 upon the gas is equal to the increase in the internal energy. W 4 = - Cv (T 2 - T 1) (4) n Total work W = W 1 + W 2 + W 3 + W 4 n n

n n According to a previous equation governing the adiabatic changes: - Combining the two equations: -
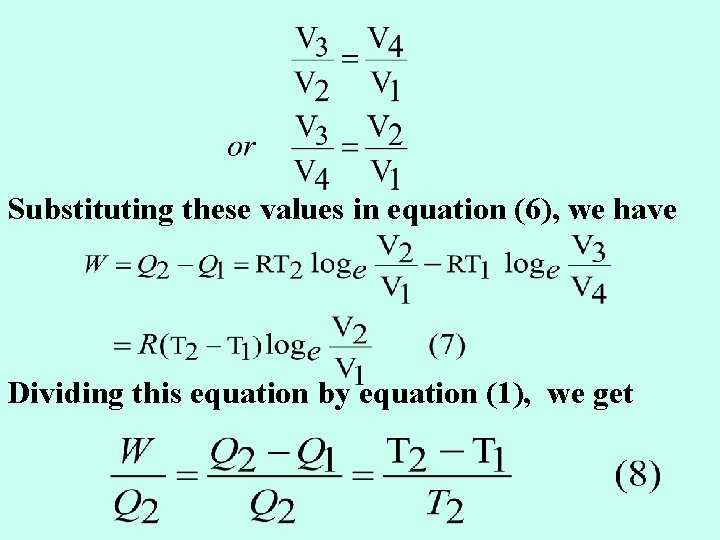
Substituting these values in equation (6), we have Dividing this equation by equation (1), we get

n n The factor W/Q 2 is called thermodynamic efficiency and given the fraction of the heat which is possible to convert into work. It is evident from the Carnot equation that the efficiency of a process depends only upon the temperature limits between which the cycle operates and is independent of all other factors. All reversible engines operating in cycle between the same temperature limits possess the same efficiency.