Chapter 3 Discrete Random Variables and Probability Distributions

Chapter 3 Discrete Random Variables and Probability Distributions § 3. 1 - Random Variables § 3. 2 - Probability Distributions for Discrete Random Variables § 3. 3 - Expected Values § 3. 4 - The Binomial Probability Distribution § 3. 5 - Hypergeometric and Negative Binomial Distributions … and Multinomial Distrib § 3. 6 - The Poisson Probability Distribution
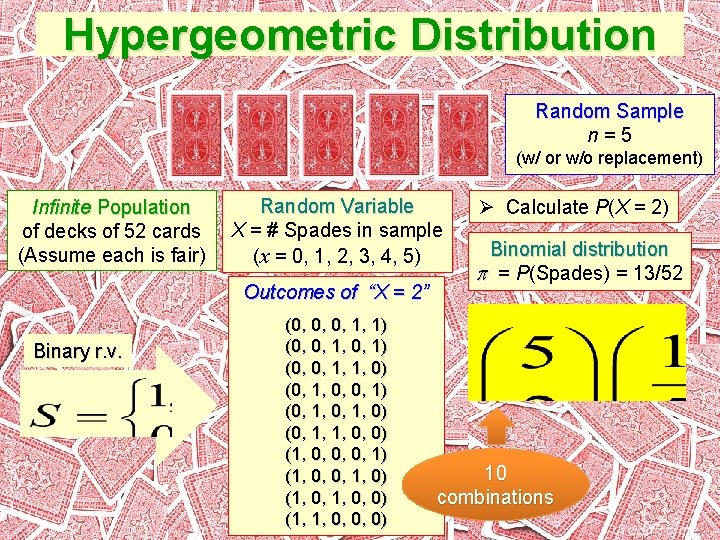
Hypergeometric Distribution Random Sample n=5 (w/ or w/o replacement) Infinite Population of decks of 52 cards (Assume each is fair) Random Variable X = # Spades in sample (x = 0, 1, 2, 3, 4, 5) Outcomes of “X = 2” Binary r. v. (0, 0, 0, 1, 1) (0, 0, 1, 1, 0) (0, 1, 0, 0, 1) (0, 1, 0) (0, 1, 1, 0, 0) (1, 0, 0, 0, 1) (1, 0, 0, 1, 0) (1, 0, 0) (1, 1, 0, 0, 0) Ø Calculate P(X = 2) Binomial distribution = P(Spades) = 13/52 10 combinations
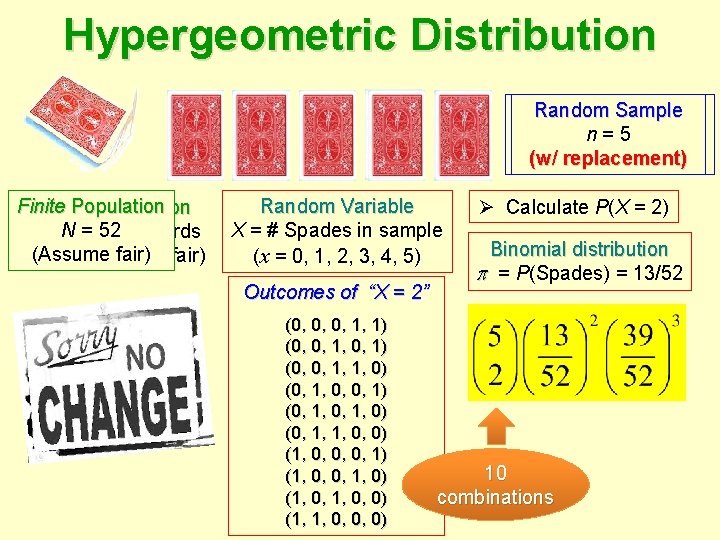
Hypergeometric Distribution Random Sample n=5 (w/ or replacement) w/o replacement) (w/ Finite Population Infinite Population N = 52 of decks of 52 cards (Assumeeach fair)is fair) (Assume Random Variable X = # Spades in sample (x = 0, 1, 2, 3, 4, 5) Outcomes of “X = 2” Binary r. v. (0, 0, 0, 1, 1) (0, 0, 1, 1, 0) (0, 1, 0, 0, 1) (0, 1, 0) (0, 1, 1, 0, 0) (1, 0, 0, 0, 1) (1, 0, 0, 1, 0) (1, 0, 0) (1, 1, 0, 0, 0) Ø Calculate P(X = 2) Binomial distribution = P(Spades) = 13/52 10 combinations
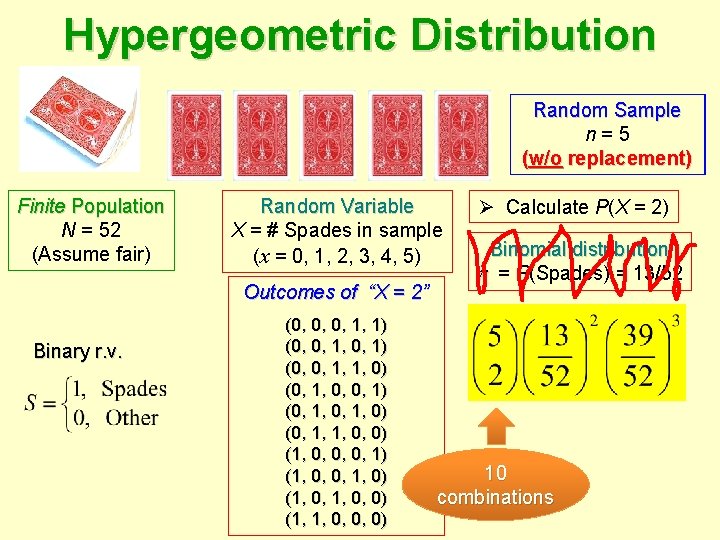
Hypergeometric Distribution Random Sample n=5 (w/o (w/ replacement) Finite Population N = 52 (Assume fair) Random Variable X = # Spades in sample (x = 0, 1, 2, 3, 4, 5) Outcomes of “X = 2” Binary r. v. (0, 0, 0, 1, 1) (0, 0, 1, 1, 0) (0, 1, 0, 0, 1) (0, 1, 0) (0, 1, 1, 0, 0) (1, 0, 0, 0, 1) (1, 0, 0, 1, 0) (1, 0, 0) (1, 1, 0, 0, 0) Ø Calculate P(X = 2) Binomial distribution = P(Spades) = 13/52 10 combinations

Hypergeometric Distribution Random Sample n=5 (w/o replacement) Finite Population N = 52 (Assume fair) Random Variable X = # Spades in sample (x = 0, 1, 2, 3, 4, 5) Outcomes of “X = 2” Binary r. v. (0, 0, 0, 1, 1) (0, 0, 1, 1, 0) (0, 1, 0, 0, 1) (0, 1, 0) (0, 1, 1, 0, 0) (1, 0, 0, 0, 1) (1, 0, 0, 1, 0) (1, 0, 0) (1, 1, 0, 0, 0) Ø Calculate P(X = 2) Binomial distribution = P(Spades) = 13/52 ? ? ? = 0. 27428

Hypergeometric Distribution Random Sample n=5 (w/o replacement) Finite Population N = 52 (Assume fair) Random Variable X = # Spades in sample (x = 0, 1, 2, 3, 4, 5) # combinations of 2 Spades from 13 Spades Ø Calculate P(X = 2) # combinations of 3 Non-Spades from 39 Non-Spades Sample Space All # combinations of 5 cards from 52 � = 0. 27428 R command: dhyper(2, 13, 39, 5) x, s, N – s, n
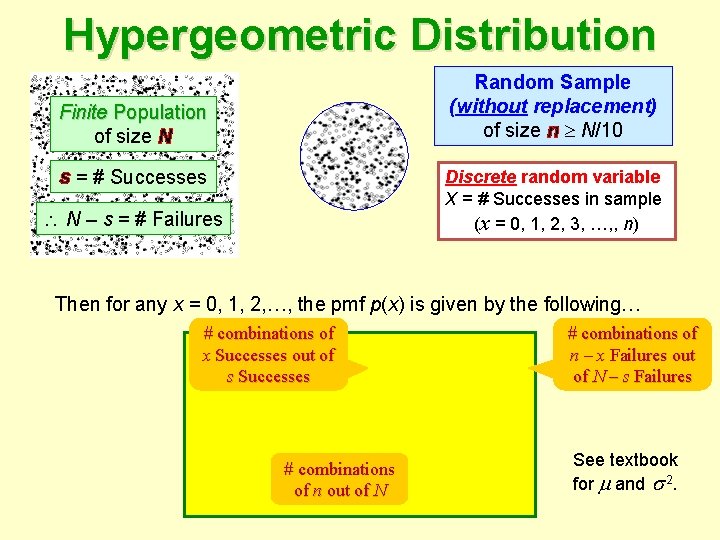
Hypergeometric Distribution Random Sample (without replacement) of size n N/10 Finite Population of size N s = # Successes Discrete random variable X = # Successes in sample (x = 0, 1, 2, 3, …, , n) N – s = # Failures Then for any x = 0, 1, 2, …, the pmf p(x) is given by the following… # combinations of x Successes out of s Successes # combinations of n out of N # combinations of n – x Failures out of N – s Failures See textbook for and 2.
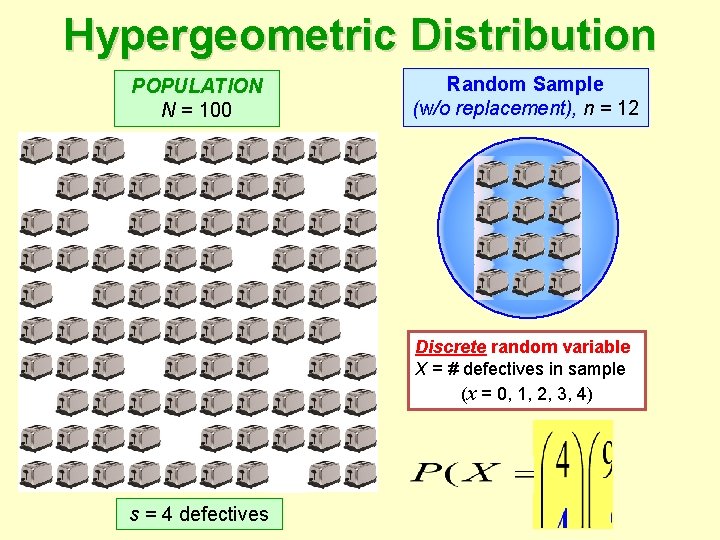
Hypergeometric Distribution POPULATION N = 100 Random Sample (w/o replacement), n = 12 Discrete random variable X = # defectives in sample (x = 0, 1, 2, 3, 4) s = 4 defectives
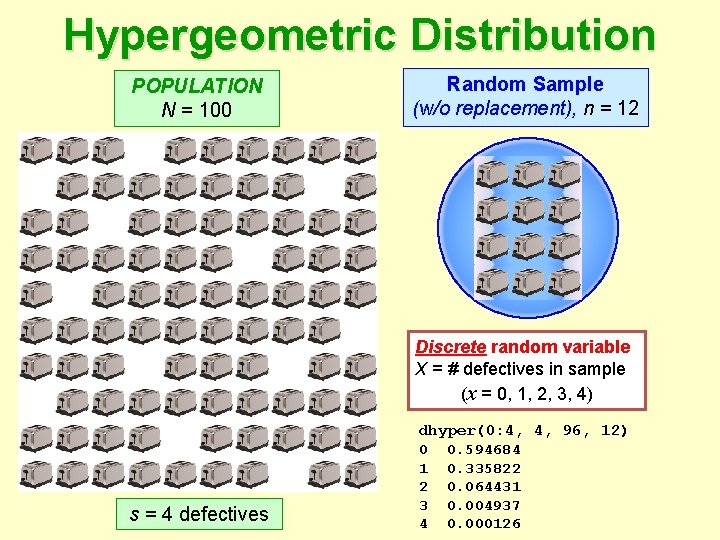
Hypergeometric Distribution POPULATION N = 100 Random Sample (w/o replacement), n = 12 Discrete random variable X = # defectives in sample (x = 0, 1, 2, 3, 4) s = 4 defectives dhyper(0: 4, 4, 96, 12) 0 0. 594684 1 0. 335822 2 0. 064431 3 0. 004937 4 0. 000126

X = # Successes (x) in n trials (x = 0, 1, 2, …, n) Classical Discrete Model Population Size Sampling: Bernoulli replacement? trials? 2 ∞ with or without yes N<∞ with yes Poisson 1 X ~ Pois( ) dpois(x, ) ∞ with or without yes Hypergeometric X ~ Hyp(x, s, N, n) N < ∞, n N/10 without no Binomial X ~ Bin(n, ) dbinom(x, n, ) dhyper(x, s, N – s, n) 1 for rare events ONLY, i. e. , small, n large 2 independent outcomes, with constant = P(Success) in population pmf p(x) P(X = x)

Negative Binomial Distribution Infinite Population of “Successes” and “Failures” Random Sample (w/ or w/o replacement) P(Success) = P(Failure) = 1 – Sample size NOT specified! Discrete random variable X = # trials for s Successes (x = s, s+1, s+2, s+3, …) Then for any x = s, s+1, s+2, …, the pmf p(x) is… dnbinom(x–s, s, ) (In R, X counts the # Failures before s Successes)

Negative Binomial Distribution = P(Spades) = 13/52 Random Sample (w/ replacement) Random Variable X = # trials for s = 6 Spades (x = 6, 7, 8, 9, 10, …)
Negative Binomial Distribution = P(Spades) = 13/52 Random Sample (w/ replacement) Random Variable 6 Spades X = # trials for s = 1 (x (x==6, 1, 7, 2, 8, 3, 9, 4, 10, …) 5, …)
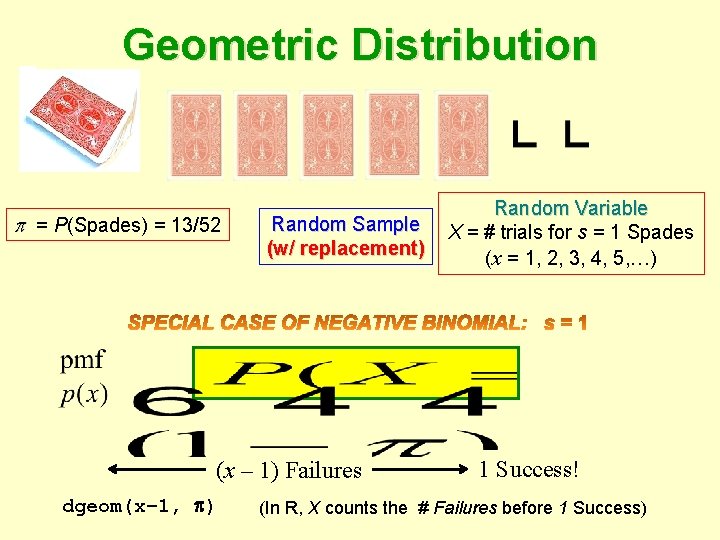
Negative Binomial Distribution Geometric Distribution = P(Spades) = 13/52 Random Sample (w/ replacement) (x – 1) Failures dgeom(x– 1, ) Random Variable X = # trials for s = 1 Spades (x = 1, 2, 3, 4, 5, …) 1 Success! (In R, X counts the # Failures before 1 Success)

Negative Binomial Distribution Geometric Distribution = P(Spades) = 13/52 Random Sample (w/ replacement) Random Variable X = # trials for s = 1 Spades (x = 1, 2, 3, 4, 5, …)
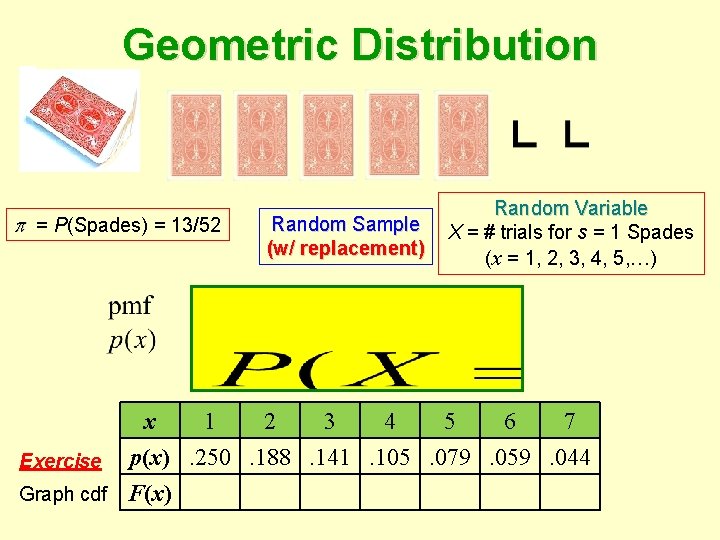
Negative Binomial Distribution Geometric Distribution = P(Spades) = 13/52 Random Sample (w/ replacement) Random Variable X = # trials for s = 1 Spades (x = 1, 2, 3, 4, 5, …) x 1 2 3 4 5 6 7 Exercise p(x). 250. 188. 141. 105. 079. 059. 044 Graph cdf F(x)

Multinomial Distribution Geometric Distribution 1 2 3 4 P(Spades) == 13/52 == P(Spades) = P(Clubs) = 13/52 = P(Hearts) = 13/52 = P(Diamonds) = 13/52 Random Sample n = 10 (w/ replacement) Random. Variables Variable Random X = #X trials s = 1 Spades 1 = #for = #2, Clubs (x. X=2 1, 3, 4, 5, …) X 3 = # Hearts X 4 = # Diamonds For i = 1, 2, 3, 4 xi = 0, 1, 2, …, 10 with x 1 + x 2 + x 3 + x 4 = 10.
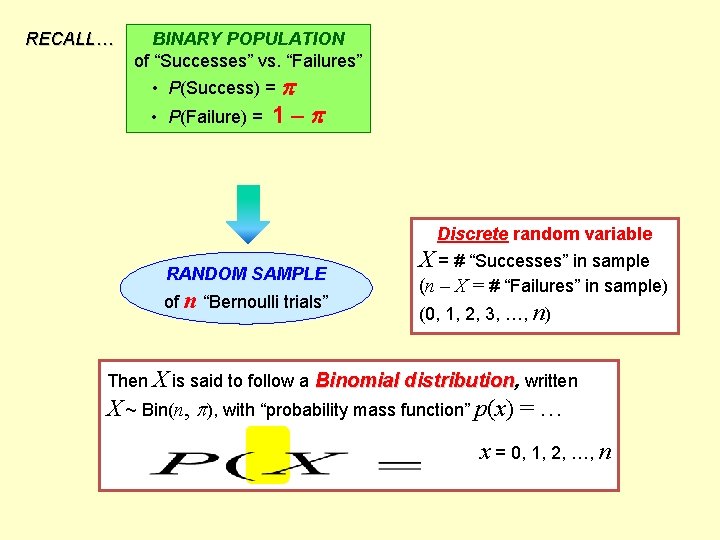
RECALL… BINARY POPULATION of “Successes” vs. “Failures” • P(Success) = • P(Failure) = 1– Discrete random variable RANDOM SAMPLE of n “Bernoulli trials” X = # “Successes” in sample (n – X = # “Failures” in sample) (0, 1, 2, 3, …, n) Then X is said to follow a Binomial distribution, written X ~ Bin(n, ), with “probability mass function” p(x) = … x = 0, 1, 2, …, n
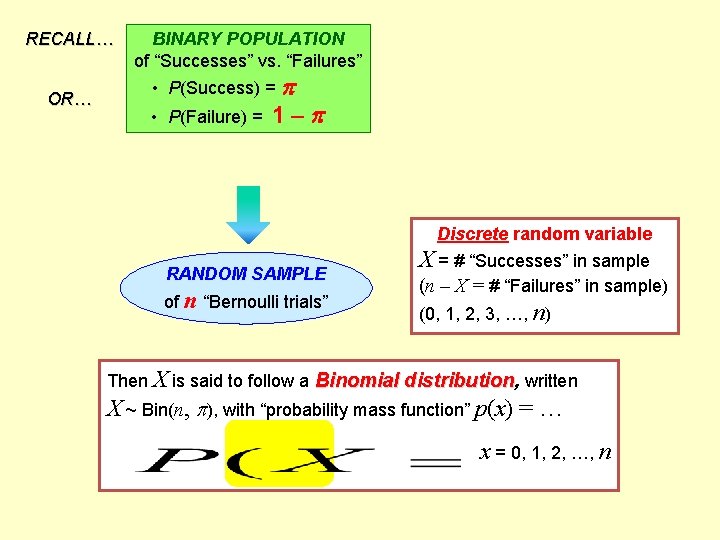
RECALL… OR… BINARY POPULATION of “Successes” vs. “Failures” • P(Success) = • P(Failure) = 1– Discrete random variable RANDOM SAMPLE of n “Bernoulli trials” X = # “Successes” in sample (n – X = # “Failures” in sample) (0, 1, 2, 3, …, n) Then X is said to follow a Binomial distribution, written X ~ Bin(n, ), with “probability mass function” p(x) = … x = 0, 1, 2, …, n
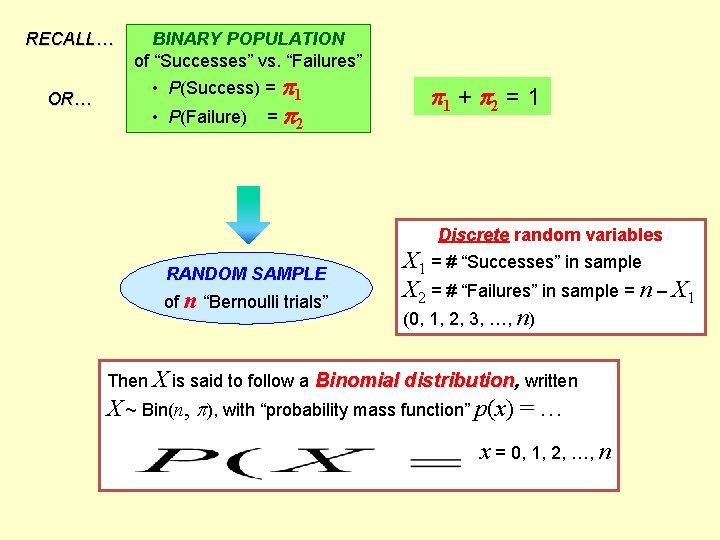
RECALL… OR… BINARY POPULATION of “Successes” vs. “Failures” • P(Success) = 1 • P(Failure) = 2 1 + 2 = 1 Discrete random variables RANDOM SAMPLE of n “Bernoulli trials” X 1 X==##“Successes”ininsample = # “Failures” in sample) X 2(n=–#X“Failures” in sample = n – X 1 (0, 1, 1, 2, 2, 3, 3, …, …, n)n) Then X is said to follow a Binomial distribution, written X ~ Bin(n, ), with “probability mass function” p(x) = … x = 0, 1, 2, …, n
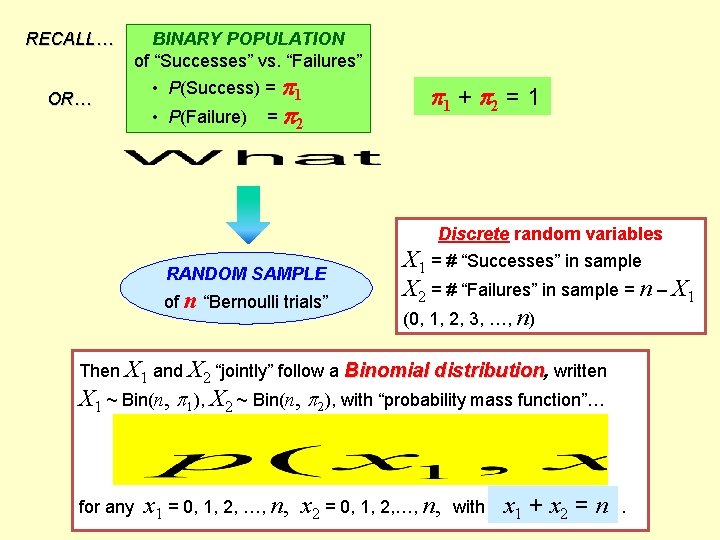
RECALL… OR… BINARY POPULATION of “Successes” vs. “Failures” • P(Success) = 1 • P(Failure) = 2 1 + 2 = 1 Discrete random variables RANDOM SAMPLE of n “Bernoulli trials” X 1 = # “Successes” in sample X 2 = # “Failures” in sample = n – X 1 (0, 1, 2, 3, …, n) Then X 1 and X 2 “jointly” follow a Binomial distribution, written X 1 ~ Bin(n, 1), X 2 ~ Bin(n, 2), with “probability mass function”… for any x 1 = 0, 1, 2, …, n, x 2 = 0, 1, 2, …, n, with x 1 + x 2 = n.
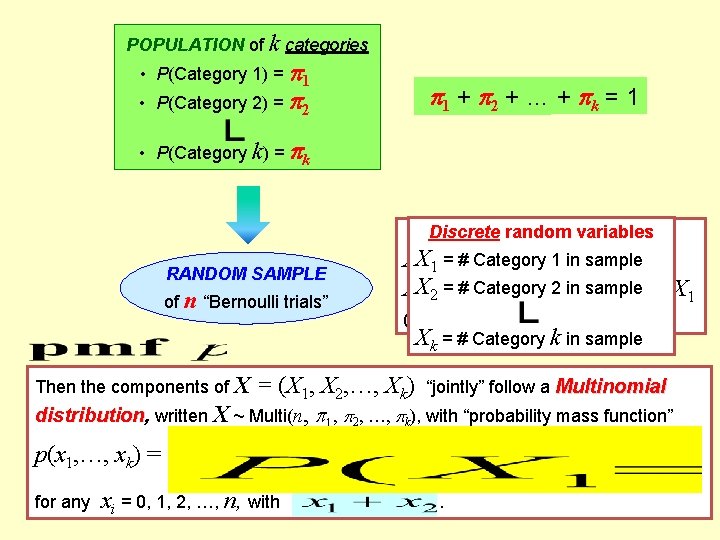
BINARY POPULATION of k categories of “Successes” vs. “Failures” • P(Category 1) = 1 • P(Success) = 1 • P(Category 2) = 2 • P(Failure) = 2 1 + 2 + =… 1 + k = 1 • P(Category k) = k RANDOM SAMPLE of n “Bernoulli trials” Discreterandomvariables Category 1 in sample XX 1 1= =# #“Successes” Categoryin 2 sample in sample XX 2 2= =# #“Failures” = n – X 1 (0, 1, 2, 3, …, n) Xk = # Category k in sample Then the components of X = (X 1, X 2, …, Xk) “jointly” follow a Multinomial distribution, written X ~ Multi(n, 1, 2, …, k), with “probability mass function” p(x 1, …, xk) = for any xi = 0, 1, 2, …, n, with .

Multinomial Distribution 1 2 3 4 = P(Spades) = 13/52 = P(Clubs) = 13/52 = P(Hearts) = 13/52 = P(Diamonds) = 13/52 Random Sample n = 10 (w/ replacement) dmultinom(c(1, 2, 3, 4), 10, c(. 25, . 25)) Random. Variables Variable Random X = #X trials s = 6 Spades 1 = #for = 7, # Clubs (x X =26, 8, 9, 10, …) X 3 = # Hearts X 4 = # Diamonds xi = 0, 1, 2, …, 10 with x 1 + x 2 + x 3 + x 4 = 10.
- Slides: 23