Binary Conversions Number systems n Binary to decimal

Binary Conversions Number systems n Binary to decimal n Decimal to binary n

Binary Humor n There are 10 kinds of people in the world those who understand binary and those who don't.

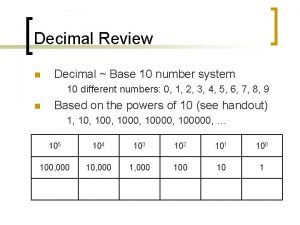
Numbering Systems n Base 10 or decimal numbering system ¨ Base-10 numbering systems dictate that the numbering scheme begins to repeat after the tenth digit (in our case, the number 9). ¨ Zero is always the first number. ¨ When we count, we usually count "00, 01, 02, 03, 04, 05 , 06, 07, 08, 09, 10, 11, 12, . . . “

Numbering Systems n Base 10 or decimal numbering system ¨ Each digit to the left and right of the decimal point is given a name which identifies that digit's placeholder. ¨ Each placeholder is a multiple of ten. ¨ For now lets just consider positive numbers.

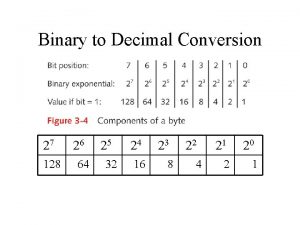
Numbering Systems - Base Ten Each placeholder is a base of ten. n 10º = ones Any number to the zero power is always equal to 1. ¨ nº=1 ¨ 10º=1 ¨ n 10¹ = tens Any number to the first power is always equal itself. ¨ n¹=n ¨ 10¹=10 ¨ n n 10² = hundreds 10³ = thousands T H O U S A N D S 7 H U N D R E D S T E N S O N E S 4 0 8

Numbering Systems – Base Ten Arithmetic expression of 8 in 7408. n Work right to left of decimal point. n The ones position in expanded notation calculating the exponent. n ¨ 10º*8=8 is the same as 1*8=8

Numbering Systems – Base Ten Number 7 4 0 8 Position Name Thousands Hundreds Tens Ones Exponential Expression 10³*7 10²*4 10¹*0 10º*8 Calculated Exponent 1000*7 100*4 10*0 1*8 Sum of the powers of ten. 1000*7 + 100*4 + 10*0 + 1*8 = 7408

Numbering Systems – Base two n n Binary system is based on multiples of two. In binary numbering the numbering scheme repeats after the second digit. Let's count to five in binary: “ 0000, 0001, 0010, 0011, 0100, 0101“ Binary numbering includes names for digit placeholders.

Numbering Systems – Base two n Picture a odometer that is only capable of counting to two.

Numbering Systems – Base two n Binary placeholders n Decimal placeholders ¨ Ones ¨ Twos ¨ Tens ¨ Fours ¨ Hundreds ¨ Eights ¨ Thousands ¨ Sixteen's ¨ Ten-thousands ¨ Thirty-twos ¨ Hundred-thousands ¨ Sixty-fours ¨ Millions

Numbering Systems – Base two If the binary system is based on powers of 2, why is there still a "ones" position? n Remember: Anything to the zero power is always equal to 1. n In binary, the "ones" position is represented by the exponential expression 2º. n

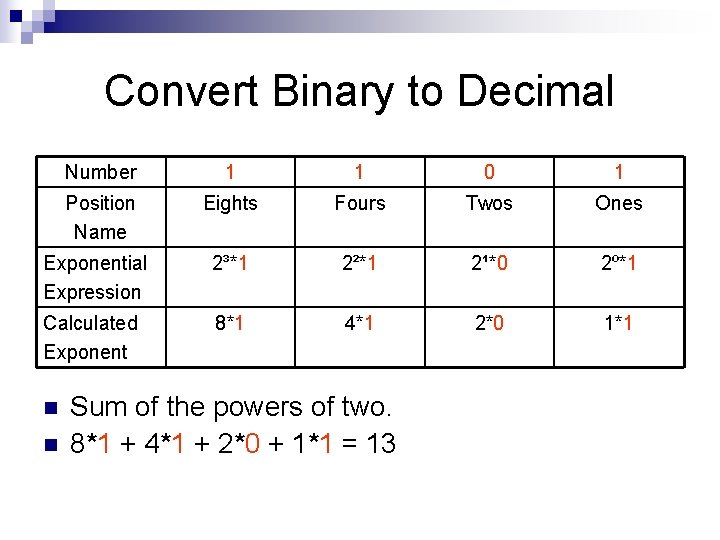
Convert Binary to Decimal Number 1 1 0 1 Position Name Eights Fours Twos Ones Exponential Expression 2³*1 2²*1 2¹*0 2º*1 Calculated Exponent 8*1 4*1 2*0 1*1 n n Sum of the powers of two. 8*1 + 4*1 + 2*0 + 1*1 = 13

Convert Binary to Decimal n Step 1 - Write the binary number in a row, separating the digits into columns. Number 1 1 0 1

Convert Binary to Decimal n n n Step 2 - I want to decide whether each digit placeholder is "ON" or "OFF. “ "1" is "ON" and a "0" is "OFF. “ We don't have to calculate any digit placeholders that are turned off. Number 1 1 0 1 ON/OFF On On Off ON

Convert Binary to Decimal n n n Step 3 - Write the exponential expressions ("powers of two") that represent each placeholder and multiply each expression by 1. We do this only for the placeholders that are turned ON. For the placeholders which are turned OFF, we simply bring down the zero from the number itself Number 1 1 0 1 ON/OFF On On Off ON Exponential Expression 2³*1 2²*1 0 2º*1

Convert Binary to Decimal n Step 4 - Calculate the exponents to get a simple multiplication expression for each placeholder. Number 1 1 0 1 ON/OFF On On Off ON Exponential Expression 2³*1 2²*1 0 2º*1 Calculated Exponent 8*1 4*1 0 1*1

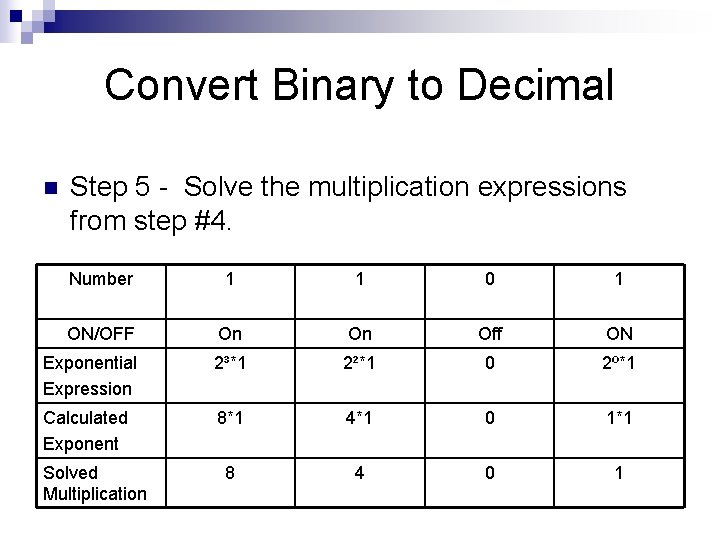
Convert Binary to Decimal n Step 5 - Solve the multiplication expressions from step #4. Number 1 1 0 1 ON/OFF On On Off ON Exponential Expression 2³*1 2²*1 0 2º*1 Calculated Exponent 8*1 4*1 0 1*1 8 4 0 1 Solved Multiplication

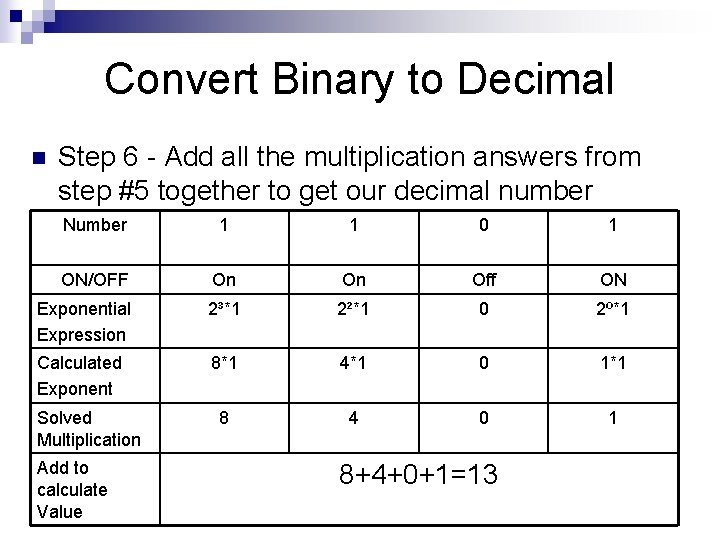
Convert Binary to Decimal n Step 6 - Add all the multiplication answers from step #5 together to get our decimal number Number 1 1 0 1 ON/OFF On On Off ON Exponential Expression 2³*1 2²*1 0 2º*1 Calculated Exponent 8*1 4*1 0 1*1 8 4 0 1 Solved Multiplication Add to calculate Value 8+4+0+1=13

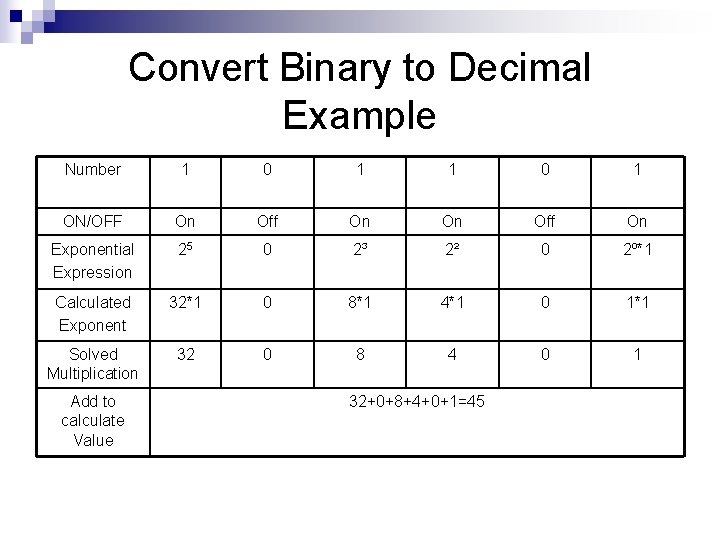
Convert Binary to Decimal Example Number 1 0 1 ON/OFF On Off On Exponential Expression 25 0 2³ 2² 0 2º*1 Calculated Exponent 32*1 0 8*1 4*1 0 1*1 Solved Multiplication 32 0 8 4 0 1 Add to calculate Value 32+0+8+4+0+1=45

Covert Decimal to Binary n n Step 1 - Take the decimal number and divide it by 2. Important: NEVER carry your divisions past the decimal point! Decimal Number=97 Division Expression 97/2 Quotient Remainder 48 1

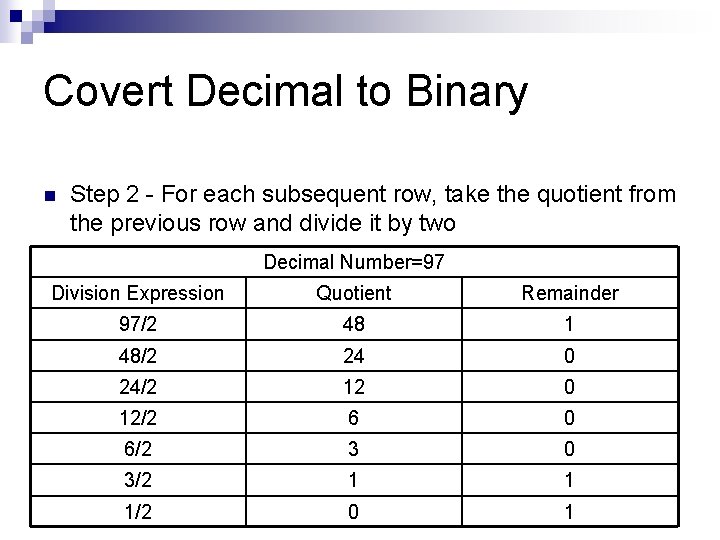
Covert Decimal to Binary n Step 2 - For each subsequent row, take the quotient from the previous row and divide it by two Decimal Number=97 Division Expression Quotient Remainder 97/2 48 1 48/2 24 0 24/2 12 0 12/2 6 0 6/2 3 0 3/2 1 1 1/2 0 1

Covert Decimal to Binary Step 3 – The remainder column only has ones or zeros. n The last cell in the remainder column of the last row must be a "1". n Read the 1 s and 0 s in the remainder column from the bottom to the top, we'll have our binary number! n

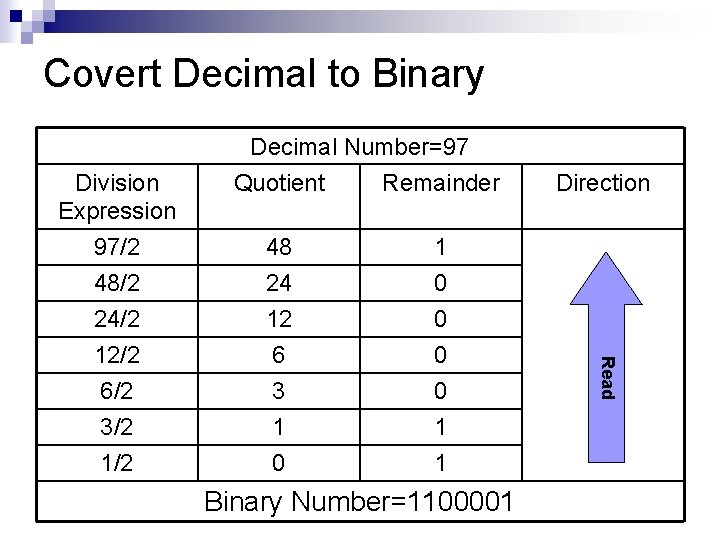
Covert Decimal to Binary Division Expression Decimal Number=97 Quotient Remainder 48 1 48/2 24/2 12/2 6/2 3/2 1/2 24 12 6 3 1 0 0 0 1 1 Binary Number=1100001 Read 97/2 Direction

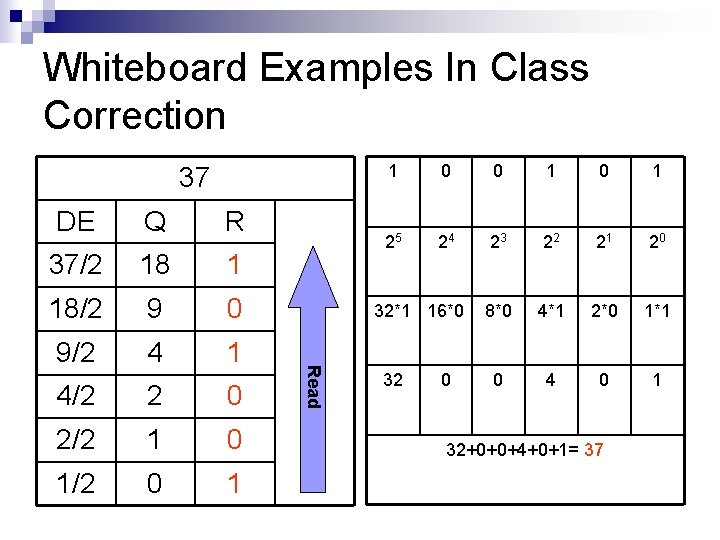
Whiteboard Examples In Class Correction 37 Q R 37/2 18 1 18/2 9 0 9/2 4 1 4/2 2 0 2/2 1 0 1/2 0 1 0 1 25 24 23 22 21 20 8*0 4*1 2*0 1*1 0 4 0 1 32*1 16*0 Read DE 1 32 0 32+0+0+4+0+1= 37

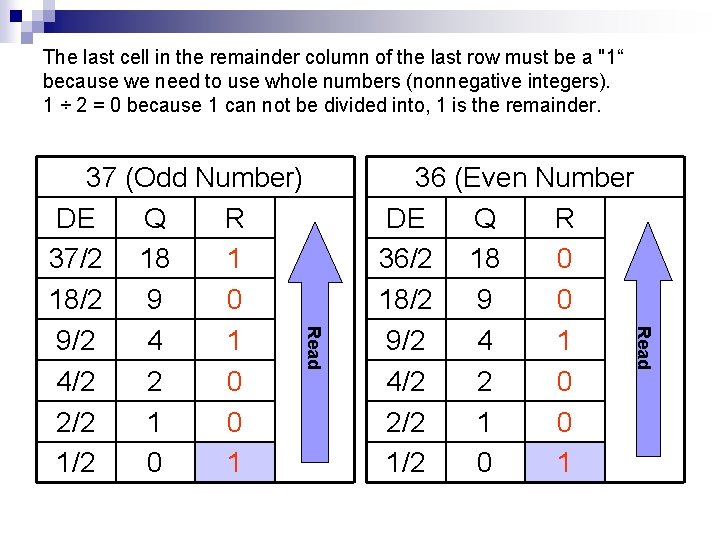
The last cell in the remainder column of the last row must be a "1“ because we need to use whole numbers (nonnegative integers). 1 ÷ 2 = 0 because 1 can not be divided into, 1 is the remainder. 36 (Even Number DE Q R 36/2 18 0 18/2 9 0 9/2 4 1 4/2 2 0 2/2 1 0 1/2 0 1 Read 37 (Odd Number) DE Q R 37/2 18 1 18/2 9 0 9/2 4 1 4/2 2 0 2/2 1 0 1/2 0 1

Hexadecimal Conversation and ASCII

Hexa + Decimal n n Base-16 number system It’s all Greek to me ¨ “Sexa” = Latin = Six ¨ “Decimal” = Latin = Ten ¨ In 1963 IBM thought “Sexadecimal” was not politically correct ¨ “Hexa” = Greek = Six ¨ Since the western alphabet contains only ten digits, hexadecimal uses the letters A-F to represent the digits ten through fifteen.

Hexadecimal and Computing n It is much easier to work with large numbers using hexadecimal values than decimal or binary. ¨ One Hexadecimal digit = 4 bits ¨ Two hexadecimal digits = 8 bits ¨ Eight bits=1 byte ¨ This makes conversions between hexadecimal and binary very easy

Counting Hexadecimal n Starting from zero, we count 00, 01, 02, 03, 04, 05, 06, 07, 08, 09, 0 A, 0 B, 0 C, 0 D, 0 E, 0 F, 10, 11, 12, 13, 14, 15, 16, 17 18, 19, 1 A, 1 B, 1 C, 1 D, 1 E, 1 F, 20, 21, 22, 23, 24, 25, . .

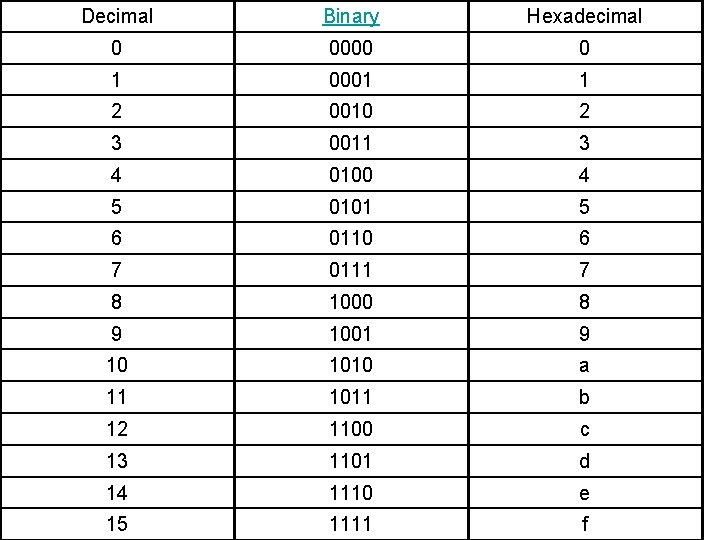
Decimal Binary Hexadecimal 0 0000 0 1 0001 1 2 0010 2 3 0011 3 4 0100 4 5 0101 5 6 0110 6 7 0111 7 8 1000 8 9 1001 9 10 1010 a 11 1011 b 12 1100 c 13 1101 d 14 1110 e 15 1111 f

Convert Hexadecimal to Decimal 1 1 A =10 8 163 162 161 160 4096*1 256*1 16*10 8*1 4096 256 160 8 4096+256+160+8= 4520

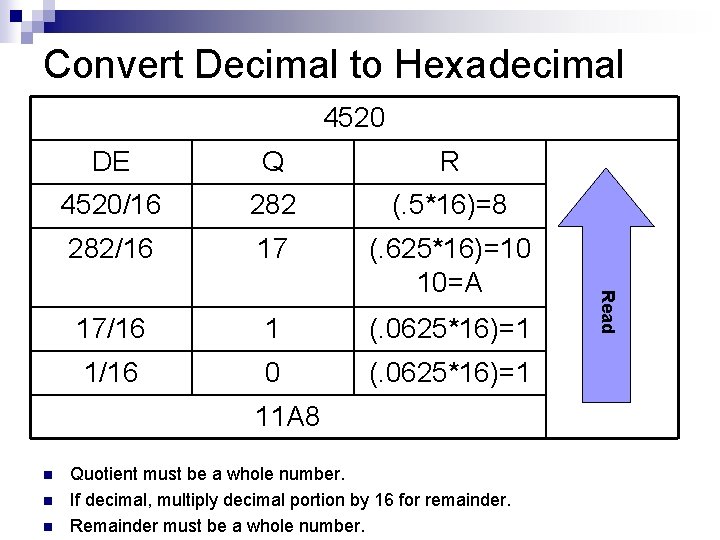
Convert Decimal to Hexadecimal 4520 Q R 4520/16 282 (. 5*16)=8 282/16 17 (. 625*16)=10 10=A 17/16 1 (. 0625*16)=1 1/16 0 (. 0625*16)=1 11 A 8 n n n Quotient must be a whole number. If decimal, multiply decimal portion by 16 for remainder. Remainder must be a whole number. Read DE

Convert Hexadecimal to Binary n n Convert each hexadecimal digit into its 4 -bit binary equivalent. 1 AB Hex Bin 1 A B 0001 1010 1011 000110101011

Convert Binary to Hexadecimal n n n Converteach 4 bit binary digit into its hexadecimal equivalent starting from the right. If there is an odd number of bits, add zeros to the left to make a complete 4 bit digit. 110101011 Bin Hex 0001 1010 1011 1 A 1 AB B

Uses ¨ Web pages n http: //www. psyclops. com/tools/rgb/ ¨ Networking n MAC address ¨ Programming n C, C++, C#, Java, Assembly ¨ Geeky T-shirts n DEADB 4 C 0 FFEE

ASCII n n n n American Standard Code for Information Interchange Each character is 7 bits + 1 bit for parity = 1 byte Represents English characters as numbers, with each letter assigned a number from 0 to 127 This makes it possible to transfer data from one computer to another. Used to store text files http: //www. pcguide. com/res/tables. ASCII-c. html http: //nickciske. com/tools/binary. php

Conversion Lab n Section I: Converting from Decimal to Binary ¨ 1) ¨ 2) ¨ 3) ¨ 4) ¨ 5) n 11 27 54 113 273 Section II: Converting from Binary to Decimal ¨ 6) 101 ¨ 7) 1011 ¨ 8) 10100 ¨ 9) 111010 ¨ 10) 1010001

Conversion Lab n n Section III: Convert Hexadecimal to Binary ¨ 11) 43 B ¨ 12) DAB ¨ 13) 954 ¨ 14) C 0 FFEE ¨ 15) B 0 A Section IV: Convert Binary to Hexadecimal ¨ 16) 11000001111 ¨ 17) 10100011110 ¨ 18) 100110 ¨ 19) 11011110 ¨ 20) 10110001

Conversion Lab n n Section V: Convert Hexadecimal to Decimal ¨ 21) FF 2 ¨ 22) 45 ¨ 23) 19 D ¨ 24) 345 ¨ 25) AA Section VI: Convert Decimal to Hexadecimal ¨ 26) 27 ¨ 27) 85 ¨ 28) 562 ¨ 29) 4522 ¨ 30) 5627