Binary FLP Number Systems Binary FLP Number System

Binary FLP Number Systems • Binary FLP Number System Ë X=(S, E, M)2 = (– 1)s (M) ( E) Ë S: Sign 0= (+) & 1= (–) Ë M: Mantissa or Significand, Ë 1>M 0. 5 or Ë 2 >M 1 Ë E: Exponent or Characteristic; biased Ë Larger Range & Less Precision ( Fixed #) 1

IEEE Standard 754 • Single-precision Format for FLP Ë 32 -bit: e=8, f=23 mantissa Ë F= (– 1)s (1. f) (2 E 127) if 254 E 1 Ë F= (– 1)s (0. f) (2 126) if E=0 Ë E=255 if f=0, for ; f 0 for NAN. • Ranges (254 E 1) Ë (2 2 23) 2254 127 F+ 1 • 21 127 2

IEEE Standard 754 (2) • Ranges (E=0) Ë (1 2 23)2 126 F+ 2 23 • 2 126 Ë Denormalized Number • May be excluded in Arith. Unit • Hidden bit: (1. f) for E 1 • 0: E=0 & f=0 3

Double-Precision Format • 64 bits e=11, f=52 mantissa Ë F= (– 1)s (1. f) (2 E 1023) if 2046 E 1 Ë Reserve values of E=0 & 2047 • Comparisons 4

General Format • F= (– 1)s (M) ( E bias) Ë 1 >M 1/ Ë =2 k • Hidden bit used Ë F= (– 1)s (0. 1 M)2 (2 E bias) Ë =2 Ë Zero? E=M=0; Smallest number E=1 5

Operations • X= ( 1)S 1 M 1 E 1 b >Y = ( 1)S 2 M 2 E 2 b • ADD/SUB Ë X Y= ( ( 1)S 1 M 1) ( 1)S 2 M 2 (E 1 E 2) ) E 1 b Ë If 1 Mnew<2 post-normalization • steps for Add/Sub: Ë difference d = | E 1 E 2 | Ë Shift smaller one d base- digit to the right Ë Add & set Enew= larger one Ë post-normalization & check OV/UV if necessary 6

Operations(2) • MUL Ë X*Y= ( ( 1)S 1 M 1) * ( 1)S 2 M 2) E 1+E 2 b b Ë Enew=E 1+E 2 b Ë If 1/ 2 Mnew <1/ post-normalization • DIV Ë Check Y=0? If Yes set NAN or Ë X/Y= ( ( 1)S 1 M 1) / ( 1)S 2 M 2) E 1 E 2+b b Ë Enew=E 1–E 2+b Ë If 1 Mnew < post-normalization 7
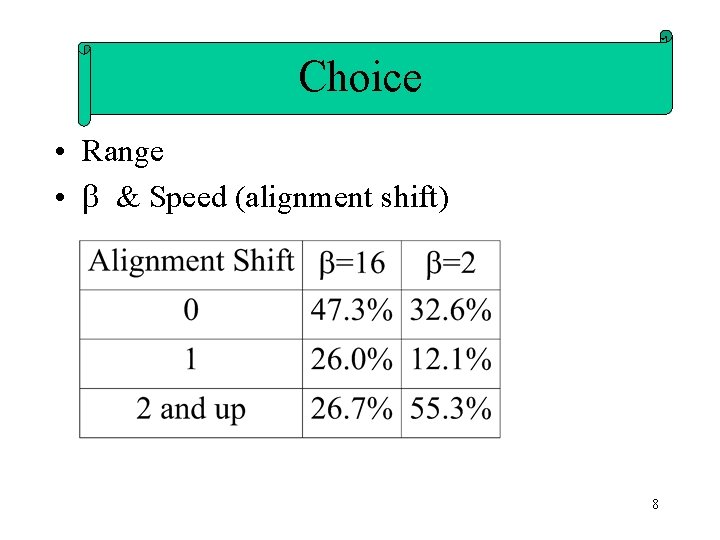
Choice • Range • & Speed (alignment shift) 8
![Choice(2) • Max. Relative Rep. Error (MRRE) =0. 5(ulp) Ë Max. [(M(x) x)/x] 0. Choice(2) • Max. Relative Rep. Error (MRRE) =0. 5(ulp) Ë Max. [(M(x) x)/x] 0.](http://slidetodoc.com/presentation_image/5ba7d09ff9b1926a5762214e36765c4e/image-9.jpg)
Choice(2) • Max. Relative Rep. Error (MRRE) =0. 5(ulp) Ë Max. [(M(x) x)/x] 0. 5(ulp) E/(M E) 0. 5(ulp) • Ave. RRE (ARRE) = (ulp)( 1)/(4 ln ) 9

Rounding • Trade-offs Ë Implementation Cost (machine) Ë Accuracy (Numerical) • Rounding Ë M(): Machine; x, y real Ë M(x) M(y) if x y Ë If x M() then M(x) = x Ë If M(y) x M(y)+ulp then M(x)=M(y) or M(x)= M(y) +ulp 10

Truncation (chopping) • • Neglect the extra LSB digit(s) M(x)=chop(x) Error=(M(x)-x) Ex. x=010. 1 then M(x)=010 11
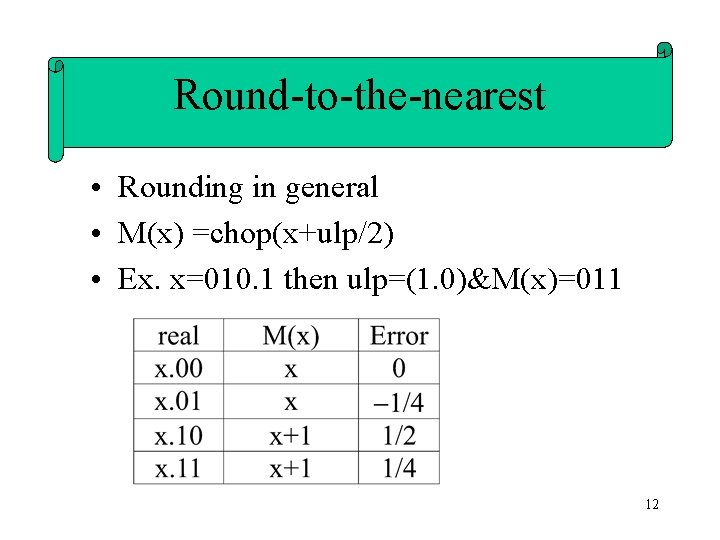
Round-to-the-nearest • Rounding in general • M(x) =chop(x+ulp/2) • Ex. x=010. 1 then ulp=(1. 0)&M(x)=011 12

Average Error • Ave. Err= Error/2 d Ë d: extra bits • Ave. Trunc. Err if fraction is rounded Ë= / 22 d = (2 d 1)/ 2 d+1 • Ave. rounding Err Ë = 0. 5/ 2 d = 1/ 2 d +1 13
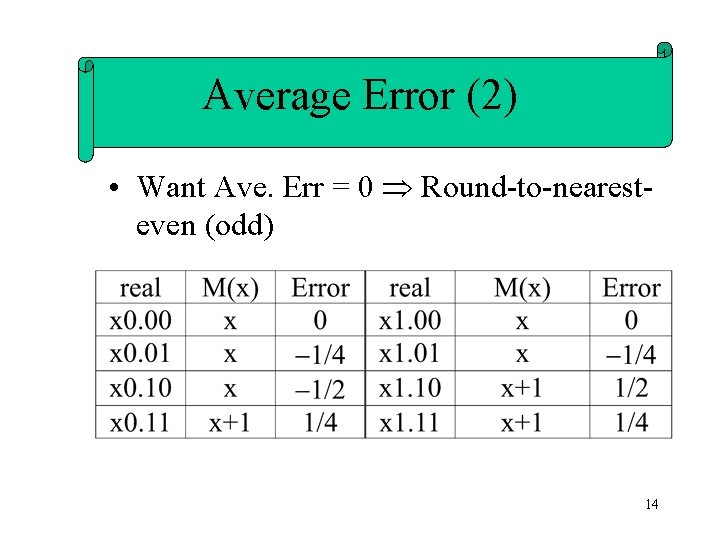
Average Error (2) • Want Ave. Err = 0 Round-to-nearesteven (odd) 14

Jamming (von Neumann) Rounding • ROM Implementation Ë M()= X(y 2 y 1 y 0. ) X(x 2 x 1 x 0. x 1 ) x 2 x 3 Ë Input= (x 2 x 1 x 0. x 1 ) Ë Output= (y 2 y 1 y 0. ) Ë (y 2 y 1 y 0. )=(x 2 x 1 x 0. ) if x 1=0 or (x 2 x 1 x 0)=(111) Ë Otherwise (y 2 y 1 y 0. )=(x 2 x 1 x 0. ) + ulp • In General Ë Input bits= c bits (include d extra bits) 15

Jamming (von Neumann) Rounding(2) Ë c=3, d=1 • Ave. Err. = 0. 5 (1/2)d 0. 5(1/2)c Ë = 0. 5(1/2)d 0. 5(1/2)c 1 Ë 1 st term= Ave Err if c >>1 16

Guard Digits • Find the smallest # of digits required • Ex 1: m=4 & No extra bit ¯ 0. 1000*2 0. 1111*20=0. 1 *2 3 ¯Missing information 17

Guard Digits(2) • Ex 2: m=3 & an extra bit(G) ¯ 0. 100*2 0. 111*2 1=0. 1001*20 0. 101 *20 ¯Rounding error! 18

Guard Digits(3) • Require two digits at least ¯Guard digit (G) ¯Round digit (R) for Round-to-the-nearest scheme • Require two digits and a sticky bit (S) ¯if Round-to-the-nearest-even (odd) scheme applied ¯S= Logic-OR all shift-out (loss) bit(s) 19

Guard Digits(4) • Ex 2: m=3 & RGS ¯LSB=RS+RS’L 20
- Slides: 20