Chapter 4 The Building Blocks Binary Numbers Boolean

Chapter 4: The Building Blocks: Binary Numbers, Boolean Logic, and Gates Invitation to Computer Science,

Objectives In this chapter, you will learn about: n The binary numbering system n Boolean logic and gates n Building computer circuits n Control circuits Invitation to Computer Science, C++ Version, Third Edition 2

Introduction n Chapter 4 focuses on hardware design (also called logic design) q q q How to represent and store information inside a computer How to use the principles of symbolic logic to design gates How to use gates to construct circuits that perform operations such as adding and comparing numbers, and fetching instructions Invitation to Computer Science, C++ Version, Third Edition 3

The Binary Numbering System n A computer’s internal storage techniques are different from the way people represent information in daily lives n Information inside a digital computer is stored as a collection of binary data q Bit = BInary digi. T Invitation to Computer Science, C++ Version, Third Edition 4

Binary Representation of Numbers n Binary numbering system q q q Base-2 Built from ones and zeros Each position is a power of 2 1101 = 1 * 23 + 1 * 22 + 0 * 21 + 1 * 20 n Decimal numbering system q q Base-10 Each position is a power of 10 3052 = 3 * 103 + 0 * 102 + 5 * 101 + 2 * 100 Invitation to Computer Science, C++ Version, Third Edition 5

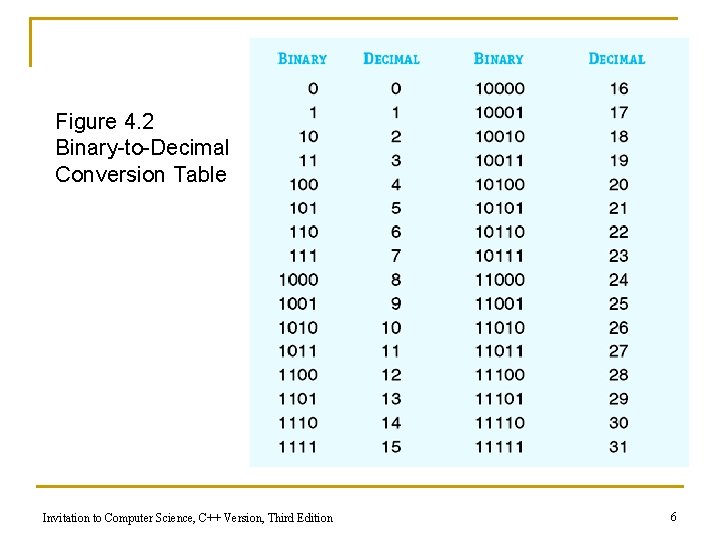
Figure 4. 2 Binary-to-Decimal Conversion Table Invitation to Computer Science, C++ Version, Third Edition 6

Conversion from Base 10 to Base 2 To convert a number n from base 10 to base 2 you must: n 1. 2. 3. Divide n by 2, then its quote by 2 and continue this way until the quote is 0 Collect all the remainders produced by the divisions performed in Step 1 Write the remainders in the opposite order they have been produced Invitation to Computer Science, C++ Version, Third Edition 7

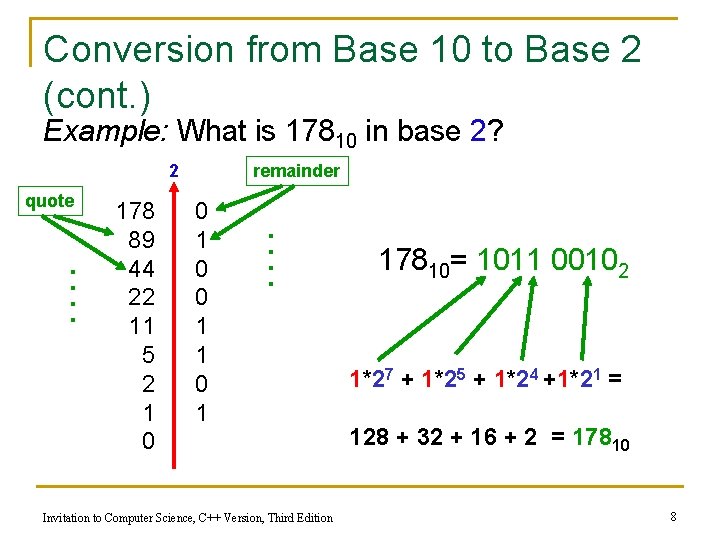
Conversion from Base 10 to Base 2 (cont. ) Example: What is 17810 in base 2? 2 quote . . 178 89 44 22 11 5 2 1 0 remainder 0 1 0 0 1 1 0 1 . . Invitation to Computer Science, C++ Version, Third Edition 17810= 1011 00102 1*27 + 1*25 + 1*24 +1*21 = 128 + 32 + 16 + 2 = 17810 8

Conversion from Base 10 to Base 2 To convert a number n from base 2 to base 10 you must: n Multiply each digit by 2 p where p is the position of the digit. 1. n 2. Of course the digits that are 0 will produce a product equal to zero, so you can limit you attention only to the digits equal to 1 Add all the products obtained in Step 1. Invitation to Computer Science, C++ Version, Third Edition 9

Conversion from Base 2 to Base 10 Example: What is 10110112 in base 10? 10112 = = 1*26 + 1*24 + 1*23 + 1*21 +1*20 = = 64 + 16 + 8 + 2 + 1 = = 9110 10112 = 9110 Invitation to Computer Science, C++ Version, Third Edition 10

Conversion from Base 10 to Base k General Rule: n To convert a number n from base 10 to base k you must: 1. 2. 3. Divide n by k, then its quote by k and continue this way until the quote is 0 Collect all the remainders produced by the divisions performed in Step 1 Write the remainders in the opposite order they have been produced Invitation to Computer Science, C++ Version, Third Edition 11

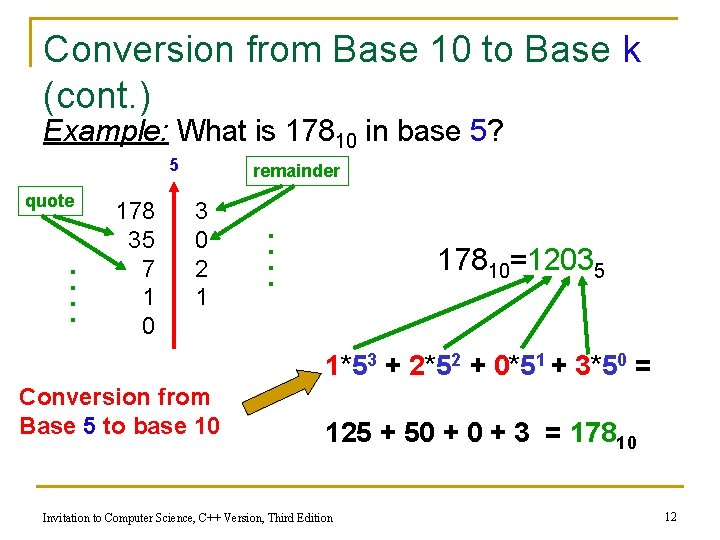
Conversion from Base 10 to Base k (cont. ) Example: What is 17810 in base 5? 5 quote . . 178 35 7 1 0 remainder 3 0 2 1 . . 17810=12035 1*53 + 2*52 + 0*51 + 3*50 = Conversion from Base 5 to base 10 125 + 50 + 3 = 17810 Invitation to Computer Science, C++ Version, Third Edition 12

Conversion from Base k to Base 10 General Rule: n To convert a number n from base k to base 10 you must: Multiply each digit by kp where p is the position of the digit. 1. n 2. Since the digits that are 0 will produce a product equal to zero, you can skip them. Add all the products obtained in Step 1. Invitation to Computer Science, C++ Version, Third Edition 13

Conversion from Base k to Base t with k and t different from 2 or 10 To convert a number n from base k to base t you must perform two conversions: n 1. 2. Convert n from base k to base 10 Convert the result from base 10 to base t Invitation to Computer Science, C++ Version, Third Edition 14

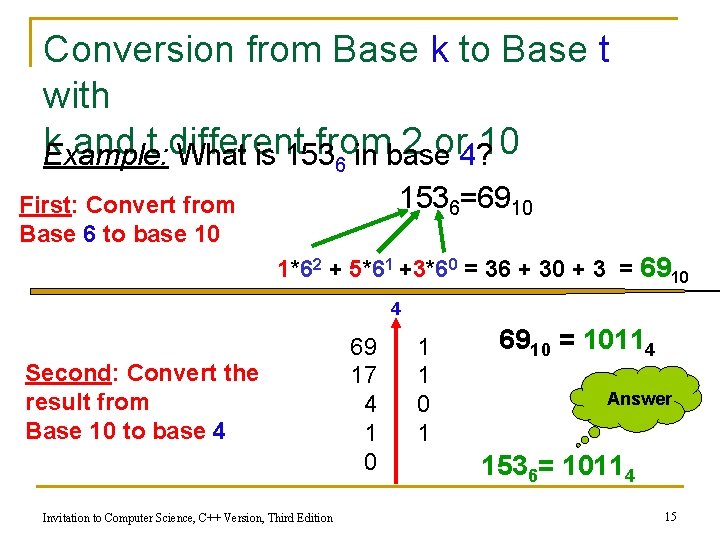
Conversion from Base k to Base t with k and t different from 2 or 10 Example: What is 153 in base 4? 6 1536=6910 First: Convert from Base 6 to base 10 1*62 + 5*61 +3*60 = 36 + 30 + 3 = 6910 4 Second: Convert the result from Base 10 to base 4 Invitation to Computer Science, C++ Version, Third Edition 69 17 4 1 0 1 6910 = 10114 Answer 1536= 10114 15

Conversion Algorithms n Base 10 is convenient for us while reading and writing numbers…. however for the machine: q n The algorithm to convert to base 10 (to display results output) and the algorithm to convert from base 10 (to insert data - input) require time. Can we display or insert data in a base different from 10? q Base 2 – n n Binary numbers are too long. Better a base closer to 10 What about 8 or 16? Invitation to Computer Science, C++ Version, Third Edition 16

Fast conversion between bases that are power of 2 n The power of 2 are special bases (ex. 4, 8, 16, . . ) q the conversion between these bases is immediate Example: Convert 37628 to base 2 n Since 8 = 23 > 2 we expand each digit in 3 binary digits q This is possible because with 3 bits we can represent 8 distinct numbers in binary 3 7 6 28 011 110 0102 Answer 37628 = 1111 00102 Invitation to Computer Science, C++ Version, Third Edition 17

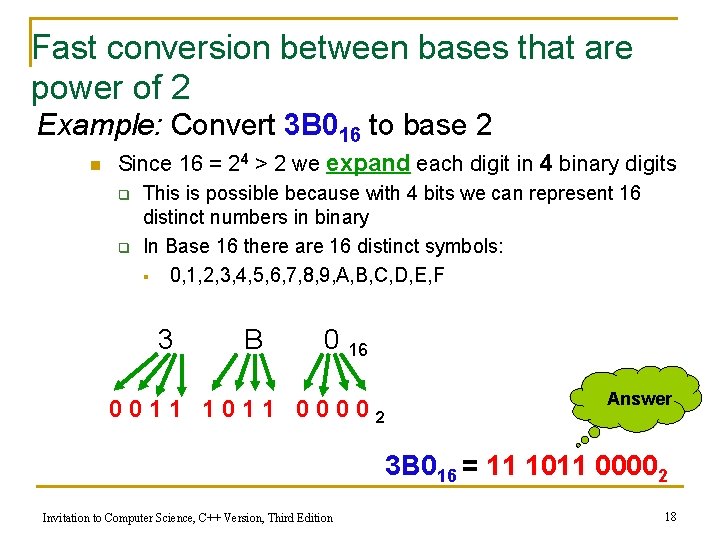
Fast conversion between bases that are power of 2 Example: Convert 3 B 016 to base 2 n Since 16 = 24 > 2 we expand each digit in 4 binary digits q q This is possible because with 4 bits we can represent 16 distinct numbers in binary In Base 16 there are 16 distinct symbols: § 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 3 B 0 16 0011 1011 00002 Answer 3 B 016 = 11 1011 00002 Invitation to Computer Science, C++ Version, Third Edition 18

Fast conversion between bases that are power of 2 Example 1: Convert 1110 10102 to base 8 n Since 2 < 8=23 we GROUP 3 binary digit in 1 octal digits 011 3 101 5 0102 1110 10102 = 3528 28 Example 2: Convert 1110 10102 to base 16 Since 2< 16 =24 we GROUP 4 binary digit in 1 hexadecimal digits § 1110 E 10102 A 16 Invitation to Computer Science, C++ Version, Third Edition 1110 10102 = EA 16 19

Converting decimal numbers in binary To convert a decimal number n= int. dec in base 2 you must: n Convert the integer part int as shown so far Convert the decimal part in this way: 1. 2. 1. 2. 3. Multiply the decimal part dec by 2, then the decimal part of the product just obtained by 2 and continue this way until the product obtained already occurred or is 0. Collect all the integer parts produced during the multiplication in Step 2. 1 Write the integers in the same order they have been produced Invitation to Computer Science, C++ Version, Third Edition 20

Converting decimal numbers in binary Example: What is 178. 2510 in base 2? 2 Step 1: Step 2: 178 89 44 22 11 5 2 1 0 0 1 1 0 1 2 0. 25 2 = 0. 5 2 = 1. 0 0 0 1 178. 2510= 1011 0010. 012 Invitation to Computer Science, C++ Version, Third Edition 21

Converting decimal numbers in binary Example: What is 0. 32510 in base 2? 2 0. 325 2 = 0. 65 2 = 1. 30 0. 30 2 = 0. 60 2 = 1. 20 0. 20 2 = 0. 40 2 = 0. 80 2 = 1. 60 0 1 period 0. 32510= 0. 0101001 2 Invitation to Computer Science, C++ Version, Third Edition 22

Summary n n n Conversion of an integer from Base 10 to Base 2 and vice versa Conversion of an integer from Base 10 to Base k and vice versa Conversion of an integer from Base k to Base t with k and t different from 2 or 10 Fast conversion between bases that are power of 2 Converting decimal numbers in binary Invitation to Computer Science, C++ Version, Third Edition 23

End of Lesson Invitation to Computer Science, C++ Version, Third Edition 24

Binary Representation of Numbers n Representing integers q Decimal integers are converted to binary integers n Given k bits, the largest unsigned integer is 2 k – 1; the smallest is 0 q q with 4 bits, the largest unsigned number is 24 -1 = 15 Signed integers must also represent the sign (positive or negative). 1 bit is used for the sign. n Given k bits, the largest signed integer is 2 k-1 - 1; the smallest is –(2 k-1 – 1) q with 4 bits, the largest signed number is 23 -1 = 7 Invitation to Computer Science, C++ Version, Third Edition 25

Representation of Numbers n Signed integer representation q Sign/magnitude notation n n 1 bit to represent the sign N bits to represent the integer q Example: if n=8 + 33 is represented as - 33 is represented as + 1 is represented as - 1 is represented as 0 0100001 1 0100001 0 0000001 1 0000001 What about 0? + 0 is represented as - 0 is represented as 0 0000000 1 0000000 Invitation to Computer Science, C++ Version, Third Edition Sign Magnitude 1 111 -7 1 110 -6 1 101 -5 1 100 -4 1 011 -3 1 010 -2 1 001 -1 1 000 -0 0 000 +0 0 001 +1 0 010 +2 0 011 +3 0 100 +4 0 101 +5 0 110 +6 0 111 +7 Big Problem!!! There are two representations for 260!!!

Representation of Numbers Signed integer representation n q Two’s complement notation a) a positive number follows the sign/magnitude notation b) a negative number is obtained from the corresponding positive number in two steps: 1. Flip all the bits (0 becomes 1 and 1 becomes 0) 2. Add one to the result Invitation to Computer Science, C++ Version, Third Edition 27

Representation of Numbers Two’s complement notation Example: assume we use 8 bits precision n Q. What is +3310 in two’s complement? A. + 3310 is represented as 0 0100001 Q. What is -3310 in two’s complement? A. - 33 is represented as 1 1011111 Step 1: take +3310 (i. e. 0 0100001) Step 2: flip it (i. e. 1 1011110) Step 3: add 1 to it 1 1011110 + 1 1 1011111 = - 3310 Invitation to Computer Science, C++ Version, Third Edition 28

Representation of Numbers Advantages of the two’s complement representation n q q One representation for the zero Easy subtractions n Subtractions are simply additions q The sign is embedded in the number! Example: Suppose we use 8 bits precision 15 0000 1111 -5 + 1111 1011 + 10 10000 1010 -9 111 10111 - 5 + 111 11011 - 14 1111 10010 overflow Invitation to Computer Science, C++ Version, Third Edition Two’s complement 1 1111 -1 1 1110 -2 1 1101 -3 1 1100 -4 1 1011 -5 1 1010 -6 1 1001 -7 1 1000 -8 1 0111 -9 1 0110 -10 1 0101 -11 1 0100 -12 1 0011 -13 1 0010 -14 1 0001 -15 1 0000 -16 00000 +0 0 0001 +1 0 0010 +2 0 0011 +3 0 0100 +4 0 0101 +5 0 0110 +6 0 0111 +7 0 1000 +8 0 1001 +9 0 1010 +10 0 1011 +11 0 1100 +12 0 1101 +13 0 1110 +14 0 1111 +15 29

Representation of Numbers Q: Given n bits precision, what is the interval of numbers that can be represented? A: n In sign/magnitude the interval is (-2 n-1, 2 n-1) q q n Note: the interval is open on both sides! There are 2 distinct representations of the 0! In two’s complement the interval is [-2 n-1, 2 n-1) q Note: the interval is open on one side! Q: With n bits, how many distinct numbers can be represented? A: 2 n distinct numbers Invitation to Computer Science, C++ Version, Third Edition 30

Representation of Numbers n Representing real numbers q Real numbers may be put into binary Scientific Notation n q q Mantissa Bases Exponent Number then are normalized so that first significant digit is immediately to the right of the binary point Then only Mantissa and Exponent are stored. Example: Consider Binary number: +6. 2510= +110. 012 is Normalized as: +. 110012 23 Invitation to Computer Science, C++ Version, Third Edition 31

Physical Representation of Numbers How to store numbers in memory: Assume that a number is stored in 16 bits storage location q q has q q 1 bit for the sign 9 bits for the mantissa 1 bit for the sign of the exponent 5 bits for the exponent +6. 2510 = +110. 012 = +. 110012 23 0 for the sign 1101 for the mantissa 0 for the sign of the exponent 3 for the exponent Decimal point and in a 16 bits storage location is represented as 011010000011 Sign Mantissa Sign Exponent 0 110010000 0 00011 Invitation to Computer Science, C++ Version, Third Edition 32

Physical Representation of Numbers: Examples 3/1610= 1/8+1/1610 = +0. 00112 = +. 112 2 -2 has 0 for the sign q 11 for the mantissa q 1 for the sign of the exponent q 2 for the exponent and in a 16 bits storage location is represented as 011000000010 Sign Mantissa Sign Exponent q 0 has 110000000 1 00010 -19/6410= 1/4+1/32+1/6410 = -0. 0100112 = -. 100112 2 -1 1 for the sign q 10011 for the mantissa q 1 for the sign of the exponent q 1 for the exponent and in a 16 bits storage location is represented as 110000100001 Sign Mantissa Sign Exponent q 1 100110000 Invitation to Computer Science, C++ Version, Third Edition 1 00001 33

Binary Representation of Numeric and Textual Information (continued) n Characters are mapped onto binary numbers q ASCII code set (look for the code in your book) n q 8 bits per character; 256 character codes UNICODE code set n 16 bits per character; 65, 536 character codes n Text strings are sequences of characters in some encoding n http: //ascii-table. com/ Invitation to Computer Science, C++ Version, Third Edition 34

Binary Representation of Sound n Multimedia data is sampled to store a digital form, with or without detectable differences n Representing sound data q q Sound data must be digitized for storage in a computer Digitizing means periodic sampling of amplitude values Invitation to Computer Science, C++ Version, Third Edition 35

Binary Representation of Sound (cont. ) q q From samples, original sound may be approximated To improve the approximation: n Sample more frequently n Use more bits for each sample value Invitation to Computer Science, C++ Version, Third Edition 36

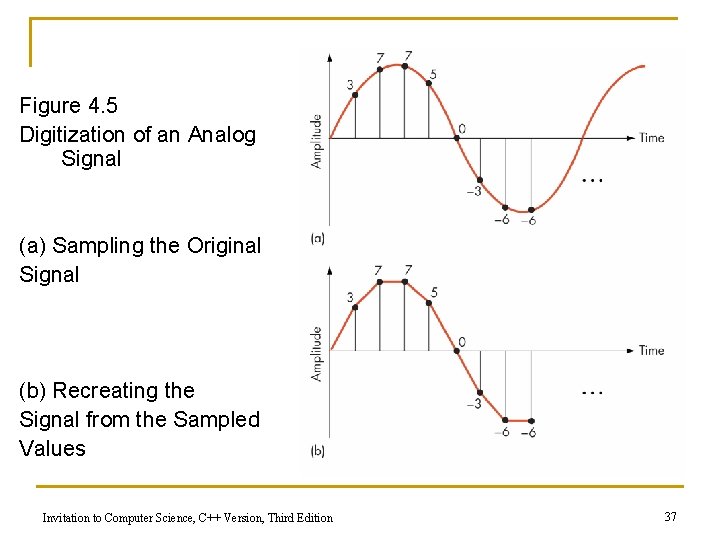
Figure 4. 5 Digitization of an Analog Signal (a) Sampling the Original Signal (b) Recreating the Signal from the Sampled Values Invitation to Computer Science, C++ Version, Third Edition 37

Binary Representation of Images n Representing image data q q q Images are sampled by reading color and intensity values at even intervals across the image Each sampled point is a pixel Image quality depends on number of bits at each pixel Invitation to Computer Science, C++ Version, Third Edition 38

Binary Representation of Images (cont. ) RGB – Encoding scheme n q 8 bits per color n q q A pixel in RGB uses 24 bits Black – absence of colors n q [0, 255] distinct values 0, 0, 0 White – all colors together n 255, 255 Example: representation of the above image in RGB 0, 0, 0 0, 0, 0 255, 255, 255 255, 255 0, 0, 0 0, 0, 0 Invitation to Computer Science, C++ Version, Third Edition 0, 0, 0 0, 0, 0 39

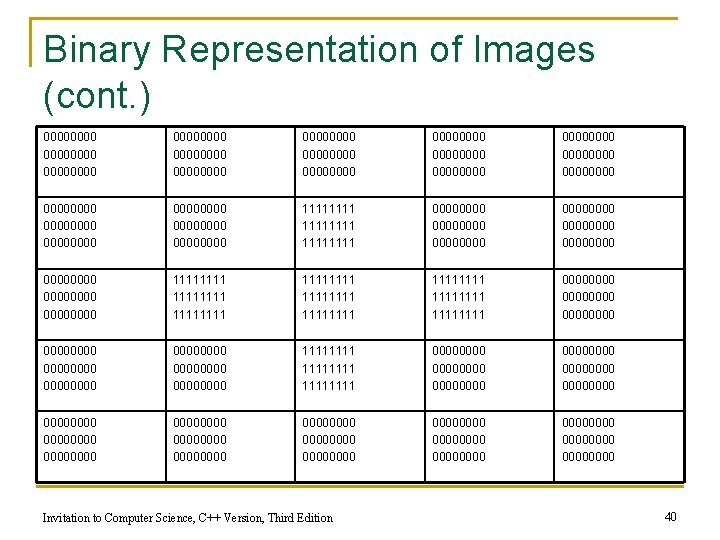
Binary Representation of Images (cont. ) 00000000 00000000 00000000 00000000 00000000 0000 11111111 00000000 00000000 0000 11111111 11111111 1111 00000000 00000000 0000 11111111 00000000 00000000 00000000 00000000 00000000 0000 Invitation to Computer Science, C++ Version, Third Edition 40

Storage size of Sound, Images, Q. What is the total number of bits required to store 3 minutes of Movies standard recording in MP 3 over two channels? n n Q. What is the total number of bits required to store a picture taken from a digital camera with 3, 500, 000 pixels? n n 44. 100 samples/sec * 16 bits/sec * 180 sec = 127, 008, 000 bits = 15, 876, 000 bytes = 15, 504 KB = 15. 1 MB per channel 15. 1 MB * 2 channels = 30. 2 MB 3, 500, 000 pixels/image * 24 bits/pixel * 1 image = 84, 000 bits = 10, 500, 000 bytes = 10, 254 KB = 10 MB Q. What is the total number of bits required to store 5 minutes a movie that shows 30 frames per second and has 3 million of pixels per frame? n 3, 000 pixels/frame * 24 bits/pixel * 30 frame/sec * 300 sec = 648, 000, 000 bits = 81, 000, 000 bytes = 79, 101, 562. 5 KB = 77, 247. 6 MB = 75. 4 GB Invitation to Computer Science, C++ Version, Third Edition 41

End of Lesson Invitation to Computer Science, C++ Version, Third Edition 42

The Reliability of Binary Representation n Electronic devices are most reliable in a bistable environment n Bistable environment q n Distinguishing only two electronic states n Current flowing or not n Direction of flow Computers are bistable: hence binary representations Invitation to Computer Science, C++ Version, Third Edition 43

Binary Storage Devices n Magnetic core q q q Historic device for computer memory Tiny magnetized rings: flow of current sets the direction of magnetic field Binary values 0 and 1 are represented using the direction of the magnetic field Invitation to Computer Science, C++ Version, Third Edition 44

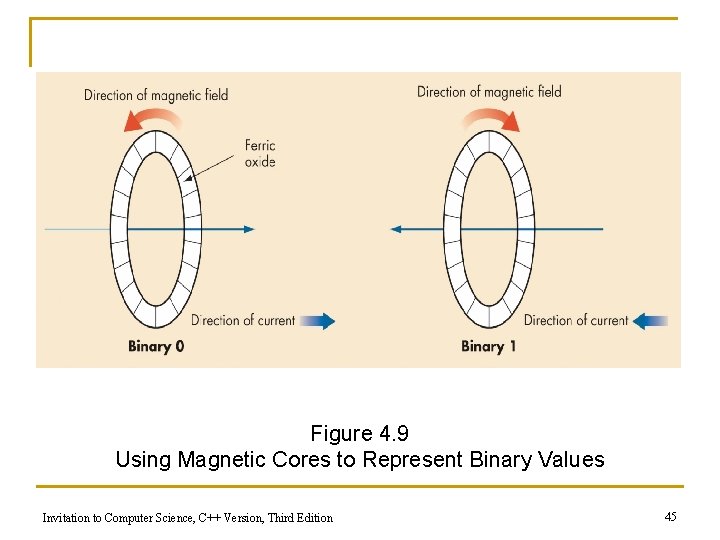
Figure 4. 9 Using Magnetic Cores to Represent Binary Values Invitation to Computer Science, C++ Version, Third Edition 45

Binary Storage Devices (continued) n Transistors q Solid-state switches: either permits or blocks current flow q A control input causes state change q Constructed from semiconductors Invitation to Computer Science, C++ Version, Third Edition 46

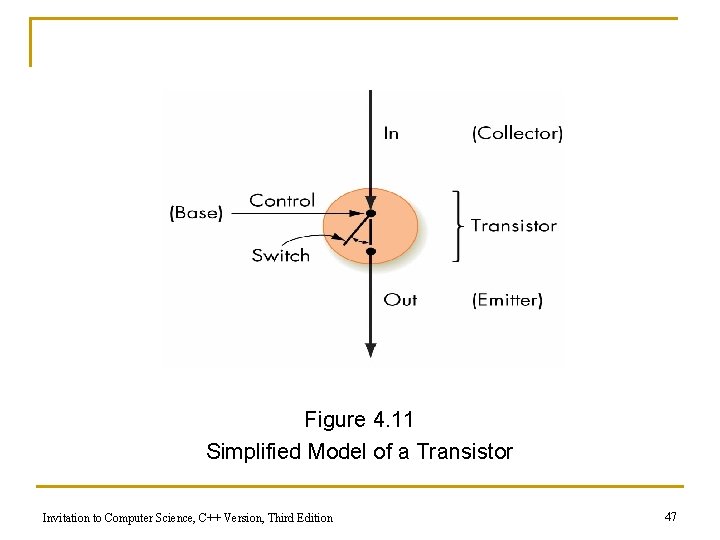
Figure 4. 11 Simplified Model of a Transistor Invitation to Computer Science, C++ Version, Third Edition 47

Boolean Logic and Gates: Boolean Logic n Boolean logic describes operations on true/false values n True/false maps easily onto bistable environment n Boolean logic operations on electronic signals may be built out of transistors and other electronic devices Invitation to Computer Science, C++ Version, Third Edition 48

Boolean Logic (continued) n Boolean operations q a AND b n q a OR b n q True only when a is true and b is true True when either a is true or b is true, or both are true NOT a n True when a is false, and vice versa Invitation to Computer Science, C++ Version, Third Edition 49

Boolean Logic (continued) n Boolean expressions q Constructed by combining together Boolean operations n n Example: (a AND b) OR ((NOT b) AND (NOT a)) Truth tables capture the output/value of a Boolean expression q A column for each input plus the output q A row for each combination of input values Invitation to Computer Science, C++ Version, Third Edition 50

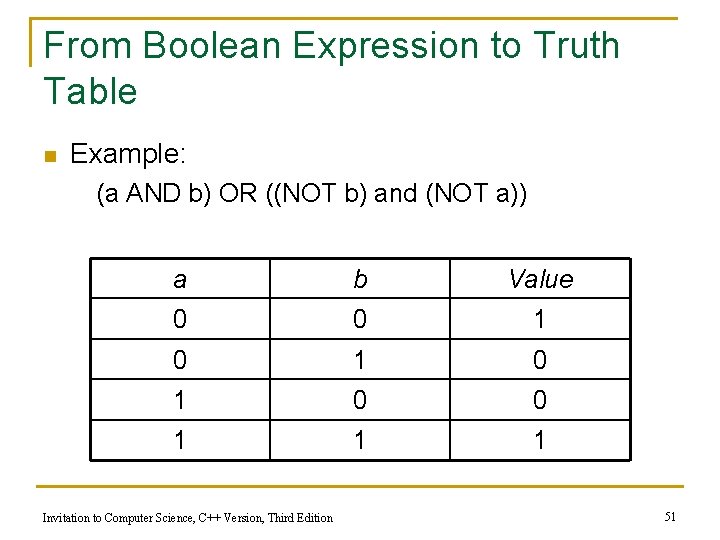
From Boolean Expression to Truth Table n Example: (a AND b) OR ((NOT b) and (NOT a)) a b Value 0 0 1 0 1 0 0 1 1 1 Invitation to Computer Science, C++ Version, Third Edition 51

Gates n Gates q n Hardware devices built from transistors to mimic Boolean logic AND gate q Two input lines, one output line q Outputs a 1 when both inputs are 1 Invitation to Computer Science, C++ Version, Third Edition 52

Gates (continued) n n OR gate q Two input lines, one output line q Outputs a 1 when either input is 1 NOT gate q One input line, one output line q Outputs a 1 when input is 0 and vice versa Invitation to Computer Science, C++ Version, Third Edition 53

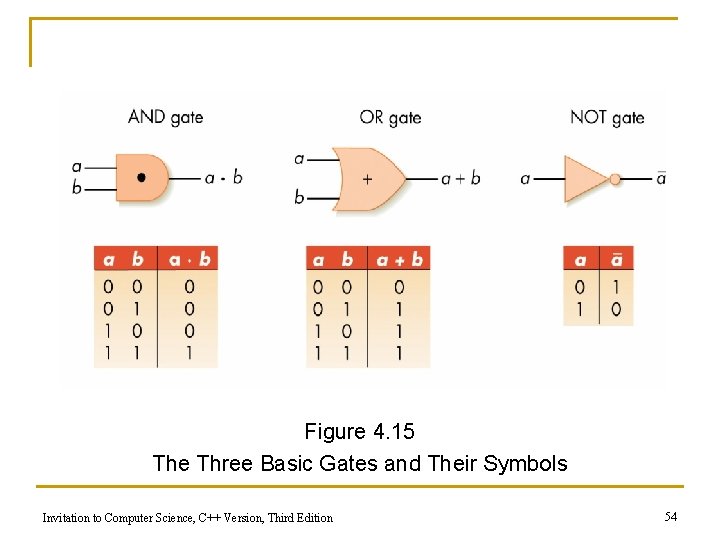
Figure 4. 15 The Three Basic Gates and Their Symbols Invitation to Computer Science, C++ Version, Third Edition 54

Gates (continued) n Abstraction in hardware design q q q Map hardware devices to Boolean logic Design more complex devices in terms of logic, not electronics Conversion from logic to hardware design may be automated Invitation to Computer Science, C++ Version, Third Edition 55

Building Computer Circuits: Introduction n A circuit is a collection of logic gates: q q n Transforms a set of binary inputs into a set of binary outputs Values of the outputs depend only on the current values of the inputs Combinational circuits have no cycles in them (no outputs feed back into their own inputs) Invitation to Computer Science, C++ Version, Third Edition 56

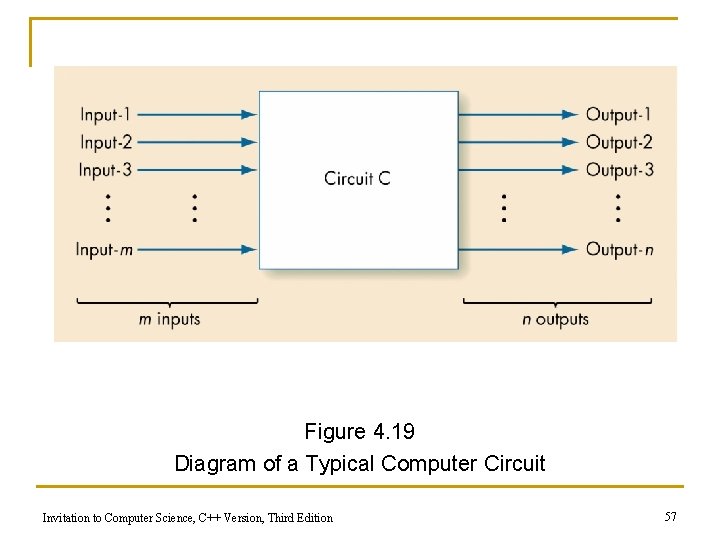
Figure 4. 19 Diagram of a Typical Computer Circuit Invitation to Computer Science, C++ Version, Third Edition 57

A Circuit Construction Algorithm n Sum-of-products algorithm is one way to design circuits: q Step 1: From Truth Table to Boolean Expression q Step 2: From Boolean Expression to Gate Layout Invitation to Computer Science, C++ Version, Third Edition 58

Figure 4. 21 The Sum-of-Products Circuit Construction Algorithm Invitation to Computer Science, C++ Version, Third Edition 59

A Circuit Construction Algorithm (continued) n Sum-of-products algorithm q q Truth table captures every input/output possible for circuit Repeat process for each output line n Build a Boolean expression using AND and NOT for each 1 of the output line n Combine together all the expressions with ORs n Build circuit from whole Boolean expression Invitation to Computer Science, C++ Version, Third Edition 60

An application of Step 1 of the SOP algorithm: From Truth Table to Boolean Expression 1. Ignore rows where the output is 0. a 0 1 b a XOR b 0 0 0 1 1 0 ab’+a’b Note: a’=NOT a b’=NOT b 2. Create the product of the selections in this way: for each row with output 1: - if the input is 1, select the variable name. - if the input is 0, select the NOT of the variable name. 3. Create the Boolean expression for the circuit by summing each of the products created in step 2. Invitation to Computer Science, C++ Version, Third Edition ==> This is the Boolean expression for the circuit to be constructed. 61

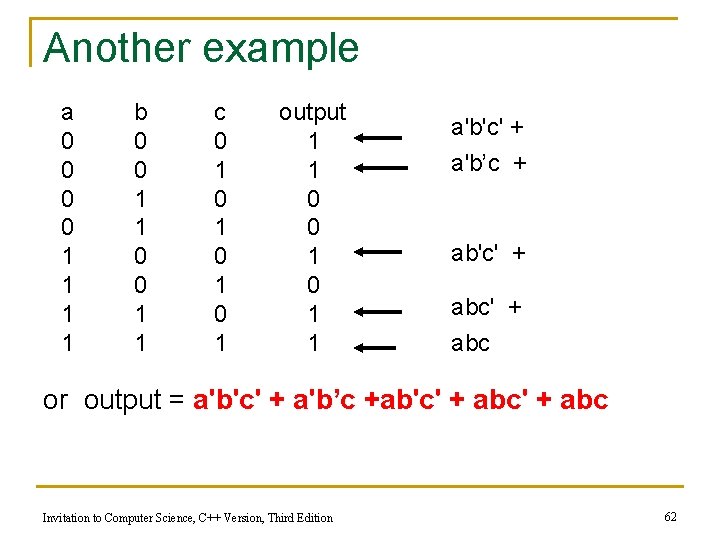
Another example a 0 0 1 1 b 0 0 1 1 c 0 1 0 1 output 1 1 0 0 1 1 a'b'c' + a'b’c + ab'c' + abc or output = a'b'c' + a'b’c +ab'c' + abc Invitation to Computer Science, C++ Version, Third Edition 62

Examples Of Circuit Design And Construction n Compare-for-equality circuit n Addition circuit n Both circuits can be built using the sum-ofproducts algorithm Invitation to Computer Science, C++ Version, Third Edition 63

A Compare-for-equality Circuit n Compare-for-equality circuit q CE compares two unsigned binary integers for equality n q q Given two n-bit numbers, a = a 0 a 1 a 2…an-1 and b = b 0 b 1 b 2…bn-1 output 1 if the numbers are the same and 0 if they are not Built by combining together 1 -bit comparison circuits (1 CE) Integers are equal if corresponding bits are equal (AND together 1 -CD circuits for each pair of bits) Invitation to Computer Science, C++ Version, Third Edition 64

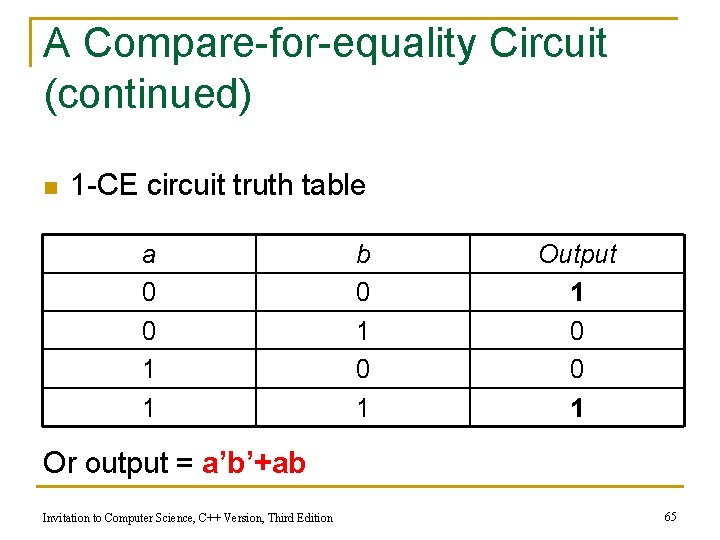
A Compare-for-equality Circuit (continued) n 1 -CE circuit truth table a 0 0 1 1 b 0 1 Output 1 0 0 1 Or output = a’b’+ab Invitation to Computer Science, C++ Version, Third Edition 65

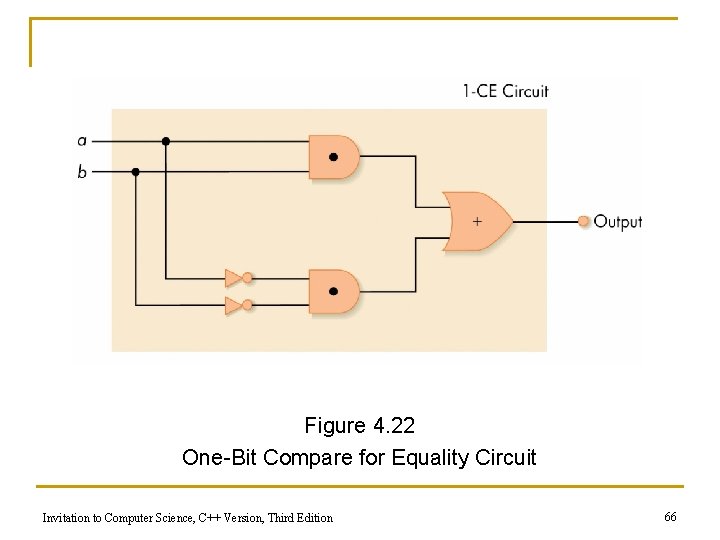
Figure 4. 22 One-Bit Compare for Equality Circuit Invitation to Computer Science, C++ Version, Third Edition 66

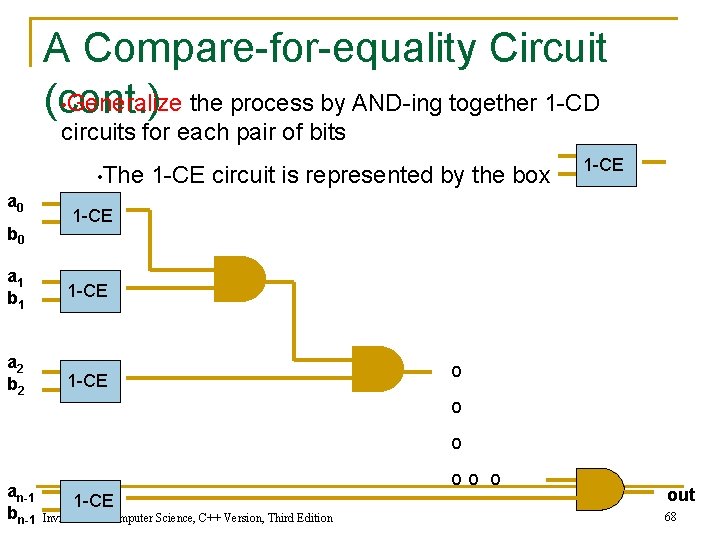
A Compare-for-equality Circuit Generalize the process by AND-ing together 1 -CD (cont. ) • circuits for each pair of bits 1 -CE • The a 0 b 0 1 -CE circuit is represented by the box 1 -CE a 1 b 1 1 -CE a 2 b 2 1 -CE o o o an-1 bn-1 oo o 1 -CE Invitation to Computer Science, C++ Version, Third Edition out 68

An Addition Circuit n Addition circuit q Adds two unsigned binary integers, setting output bits and an overflow q Built from 1 -bit adders (1 -ADD) q Starting with rightmost bits, each pair produces n A value for that order (i. e. si=ai+bi) n A carry bit for next place to the left (i. e. ci) Invitation to Computer Science, C++ Version, Third Edition 69

An Addition Circuit (continued) n 1 -ADD truth table q q Input n One bit from each input integer n One carry bit (always zero for rightmost bit) Output n One bit for output place value n One “carry” bit Invitation to Computer Science, C++ Version, Third Edition 70

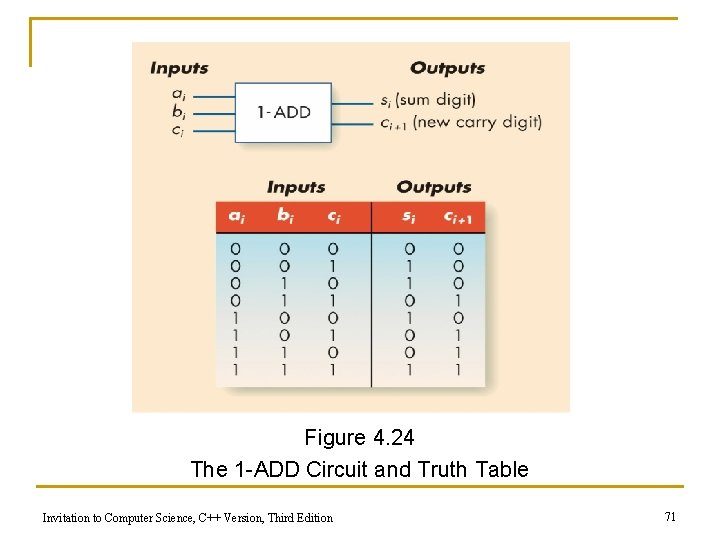
Figure 4. 24 The 1 -ADD Circuit and Truth Table Invitation to Computer Science, C++ Version, Third Edition 71

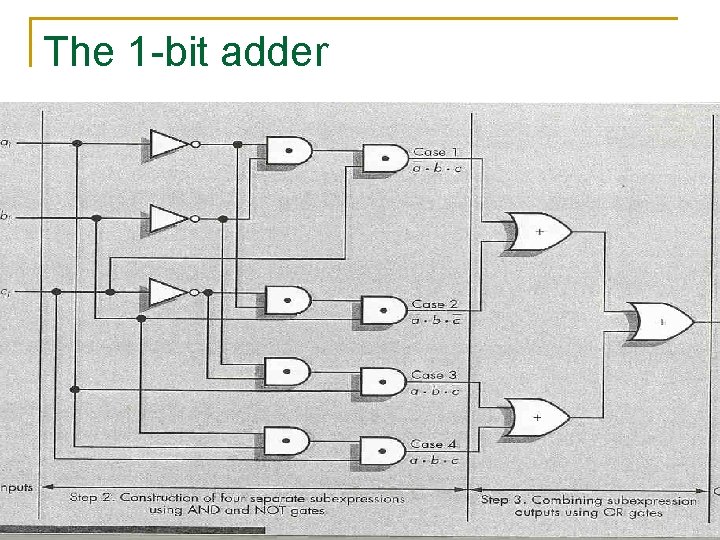
The 1 -bit adder Invitation to Computer Science, C++ Version, Third Edition 72

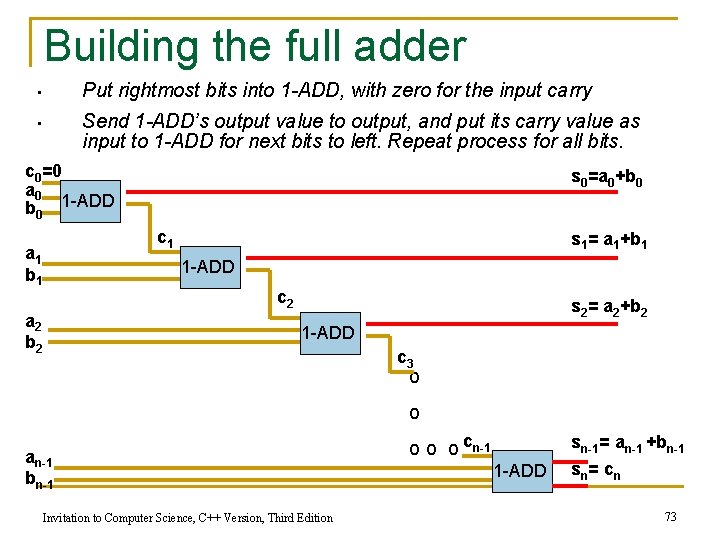
Building the full adder • Put rightmost bits into 1 -ADD, with zero for the input carry • Send 1 -ADD’s output value to output, and put its carry value as input to 1 -ADD for next bits to left. Repeat process for all bits. c 0=0 a 0 b 0 1 -ADD s 0=a 0+b 0 c 1 a 1 b 1 s 1= a 1+b 1 1 -ADD c 2 a 2 b 2 s 2= a 2+b 2 1 -ADD c 3 o o an-1 bn-1 Invitation to Computer Science, C++ Version, Third Edition o o o cn-1 sn-1= an-1 +bn-1 1 -ADD sn= c n 73

Control Circuits n Do not perform computations n Choose order of operations or select among data values n Major types of controls circuits q Decoders n q Multiplexors n n Sends a 1 on one output line, based on what input line indicates Select one of inputs to send to output We will use these control circuits while studying next chapter. Invitation to Computer Science, C++ Version, Third Edition 74

Control Circuits (Decoder) n Decoder q q q Form n N input lines n 2 N output lines N input lines indicate a binary number, which is used to select one of the output lines Selected output sends a 1, all others send 0 Invitation to Computer Science, C++ Version, Third Edition 75

Control Circuits (continued) n Decoder purpose q q q Given a number code for some operation, trigger just that operation to take place Numbers might be codes for arithmetic: add, subtract, etc. Decoder signals which operation takes place next Invitation to Computer Science, C++ Version, Third Edition 76

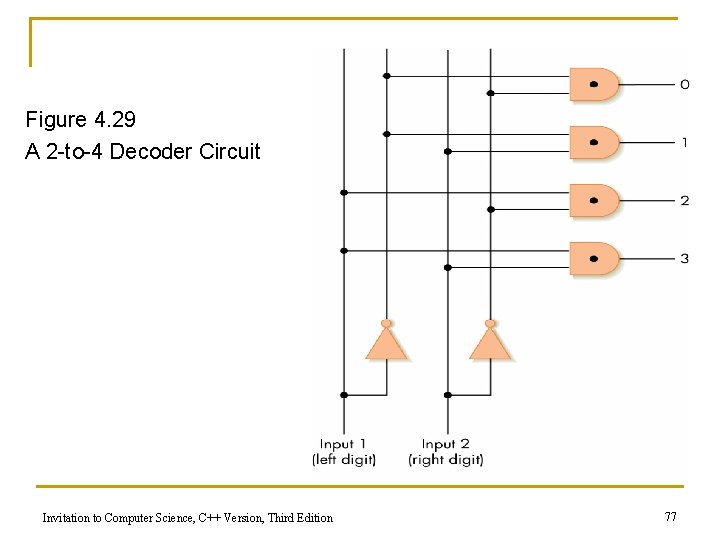
Figure 4. 29 A 2 -to-4 Decoder Circuit Invitation to Computer Science, C++ Version, Third Edition 77

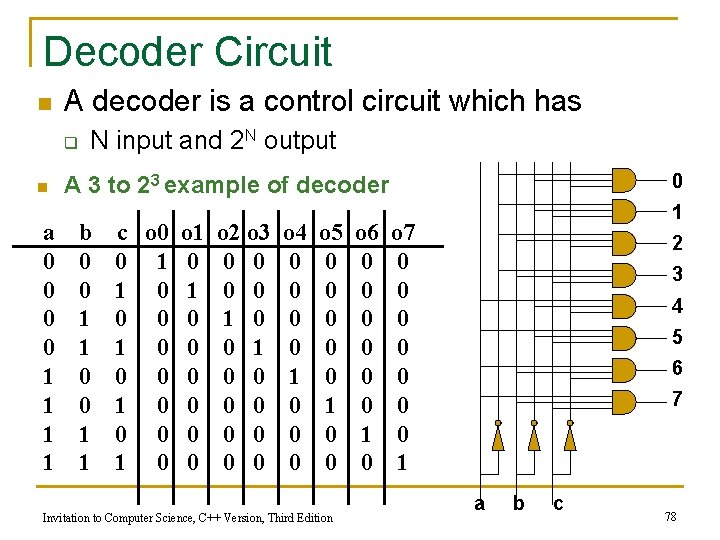
Decoder Circuit n A decoder is a control circuit which has q n a 0 0 1 1 N input and 2 N output 0 A 3 to 23 example of decoder b 0 0 1 1 c o 0 o 1 0 1 0 0 0 0 0 1 0 0 o 2 o 3 0 0 1 0 0 0 0 0 o 4 0 0 1 0 0 0 o 5 0 0 0 1 0 0 Invitation to Computer Science, C++ Version, Third Edition o 6 0 0 0 1 0 1 o 7 0 0 0 0 1 2 3 4 5 6 7 a b c 78

Control Circuits (Multiplexor) n n Multiplexor form q 2 N regular input lines q N selector input lines q 1 output line Multiplexor purpose q q Given a code number for some input, selects that input to pass along to its output Used to choose the right input value to send to a computational circuit Invitation to Computer Science, C++ Version, Third Edition 79

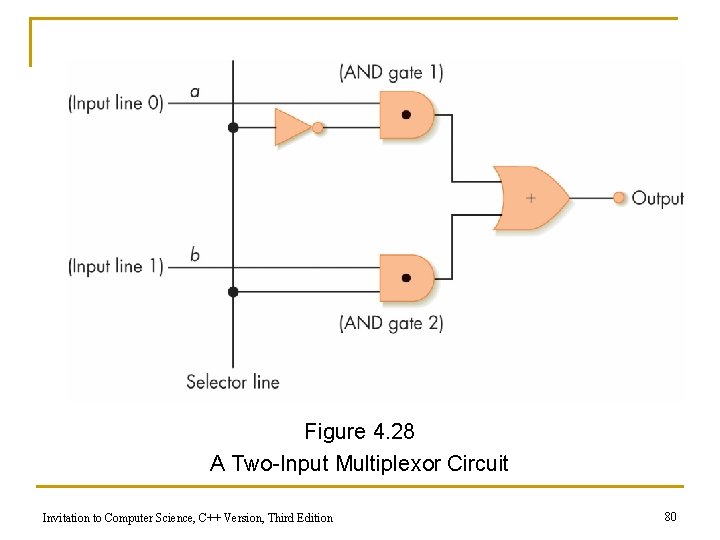
Figure 4. 28 A Two-Input Multiplexor Circuit Invitation to Computer Science, C++ Version, Third Edition 80

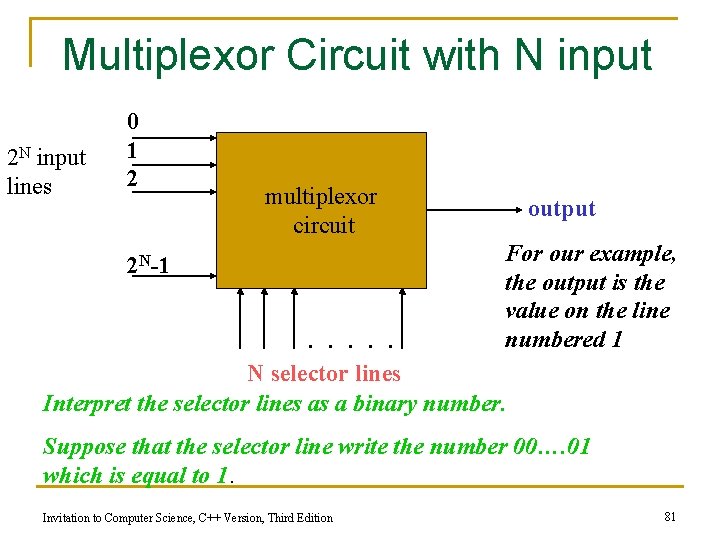
Multiplexor Circuit with N input 2 N input lines 0 1 2 multiplexor circuit 2 N-1 . . . output For our example, the output is the value on the line numbered 1 N selector lines Interpret the selector lines as a binary number. Suppose that the selector line write the number 00…. 01 which is equal to 1. Invitation to Computer Science, C++ Version, Third Edition 81

Summary n n n Digital computers use binary representations of data: numbers, text, multimedia Binary values create a bistable environment, making computers reliable Boolean logic maps easily onto electronic hardware Circuits are constructed using Boolean expressions as an abstraction Computational and control circuits may be built from Boolean gates Invitation to Computer Science, C++ Version, Third Edition 82