Autmatas Finitos Es un diagrama de transiciones que

Autómatas Finitos ● ● Es un diagrama de transiciones que permite identificar cadenas que pertenecen a un lenguaje. Puede ser determinista o no determinista. En los No deterministas los estados pueden tener más de una transición y existen transiciones epsilon. En los deterministas cada estado tiene una única transición.

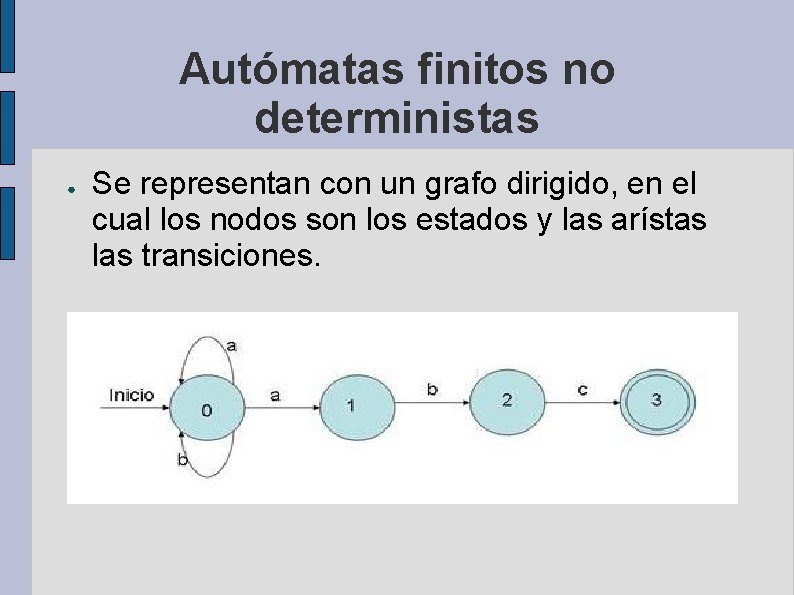
Autómatas finitos no deterministas ● Se representan con un grafo dirigido, en el cual los nodos son los estados y las arístas las transiciones.

Autómatas finitos deterministas ● ● No hay transiciones epsilon Para cada estado existe una única transición Existe solo un camino desde el estado inicial En la tabla de transiciones cada entrada es un estado.

Conversión de AFN a AFD ● ● Se construye una tabla de transiciones donde cada estado de la tabla es un conjunto de estados del AFN. Sobre esto se realizan las siguientes operaciones. Cerradura -e (s), representa los estados alcanzables desde el estado s a través de transiciones epsilon.

Conversión de AFN a AFD [2] ● ● Cerradura -e (T) representa los estados alcanzables desde el estado s en T através des transiciones epsilon. Cerradura -e (T, a) hay una transición de con entrada a desde algún estado s en T

● Conversión a un Autómata Finito Determinista estados. D=cerradura-ε(S 0) al comienzo es el único estado dentro de estados. D aún sin marcar. while (haya un estado no marcado T en estados. D) { marcar T; for (cada símbolo de entrada a) { U= cerradura-ε(mueve(T, a)); if (U no está en estados. D) { añadir U como estado no marcado a estados. D; } tran. D[T, a] = U; } }

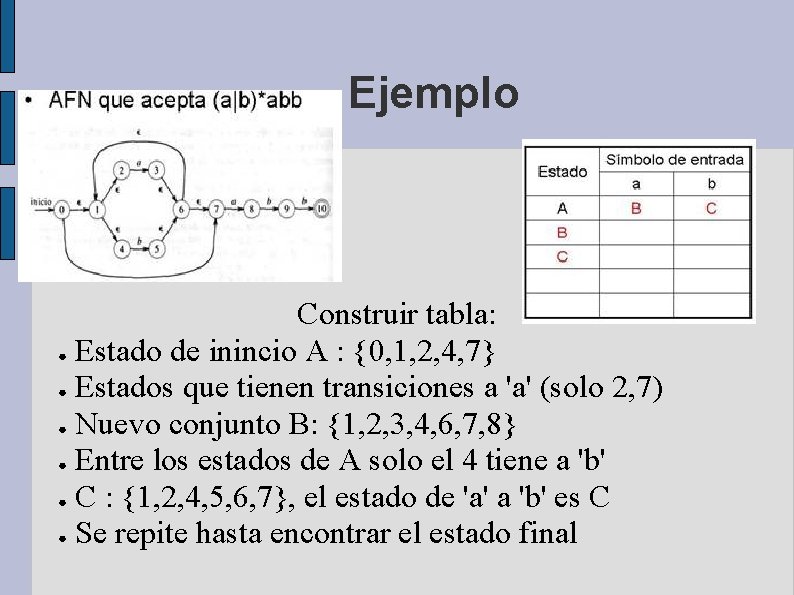
Ejemplo Construir tabla: ● Estado de inincio A : {0, 1, 2, 4, 7} ● Estados que tienen transiciones a 'a' (solo 2, 7) ● Nuevo conjunto B: {1, 2, 3, 4, 6, 7, 8} ● Entre los estados de A solo el 4 tiene a 'b' ● C : {1, 2, 4, 5, 6, 7}, el estado de 'a' a 'b' es C ● Se repite hasta encontrar el estado final

Propiedades algebraicas de las expresiones regulares