Tcnicas de Estados Finitos Introduccin Autmatas de estados

Técnicas de Estados Finitos • • Introducción Autómatas de estados finitos (FSA) Transductores de estados finitos (FST) FST en Xerox MLTT PLN Técnicas de Estados Finitos 1

Técnicas de Estados Finitos 1 • Aplicaciones: Uso creciente en PLN • morfología • fonología • generación léxica • reconocimiento del habla • tagging • simplificación de CFG • Extracción de Información PLN Técnicas de Estados Finitos 2

Técnicas de Estados Finitos 2 • Razón: • Eficiencia temporal y espacial • Las (algunas) máquinas de estados finitos pueden hacerse deterministas y pueden expresarse en forma (más) compacta • Referencias • Software PLN Técnicas de Estados Finitos Roche, Schabes, 1997 Kornai, 1999 Jurafsky, Martin, 2000 (cap. 2 y 3) Cases, Màrquez, 2000 ATT http: //www. research. att. com/sw/tools/lextools/ Xerox Multilingual Theory and Technology http: //www. rxrc. xerox. com/research/mltt/ Carmel http: //www. isi. edu/licensed-sw/carmel/ 3

FSA 1 • Equivalencia entre • expresiones regulares • lenguajes regulares • FSA PLN Técnicas de Estados Finitos 4

Expresiones regulares 1 • Básicamente son combinaciones de expresiones simples (letras o strings) con operaciones de concatenación, disyunción, etc. • ejemplos: • comandos unix como awk, gerp, egrep • lenguaje de Xerox • Perl, Python, . . . • Ejemplo: grep <pattern> <file> • 'te', '[Tt]e', '[aeiou][aeiou]', '[a-z, A-Z]', '[0 -9]', '[^aeiou][^aeiou]', 'vand. lico', '^[aeiou][az]*ón$', '(ón|ona)$' PLN Técnicas de Estados Finitos 5

Expresiones regulares 2 • patterns acrophile (localización de acrónimos) • • • acro 1 = re. compile('^([A-Z][, . -/_])+$') acro 2 = re. compile('^([A-Z])+$') acro 3 = re. compile('^d*[A-Z](d[A-Z])*$') acro 4 = re. compile('^[A-Z][A-Z]+[A-Za-z]+$') acro 5 = re. compile('^[A-Z]+[A-Za-z]+[A-Z]+$') acro 6 = re. compile('^([A-Z][, . -/_]){2, 9}('s|s)? $') acro 7 = re. compile('^[A-Z]{2, 9}('s|s)? $') acro 8 = re. compile('^[A-Z]*d[-_]? [A-Z]+$') acro 9 = re. compile('^[A-Z]+[A-Za-z]+[A-Z]+$') acro 10 = re. compile('^[A-Z]+[/-][A-Z]+$') PLN Técnicas de Estados Finitos 6

Lenguajes formales • • • Alfabeto (vocabulario) Operación de concatenación * cadenas sobre (monoide libre) lenguaje L * lenguajes y gramáticas lenguajes regulares (RL) PLN Técnicas de Estados Finitos 7

Operaciones sobre lenguajes formales • • L, L 1 y L 2 son lenguajes operaciones • concatenación • unión • intersección • diferencia • complemento PLN Técnicas de Estados Finitos 8

FSA 2 • • < , Q, i, F, E> Q i Q F Q E Q ( { }) Q E: {d | d: Q ( { }) 2 Q} PLN Técnicas de Estados Finitos alfabeto conjunto finito de estados estado inicial conjunto de estados finales conjunto de arcos conjunto de transiciones 9

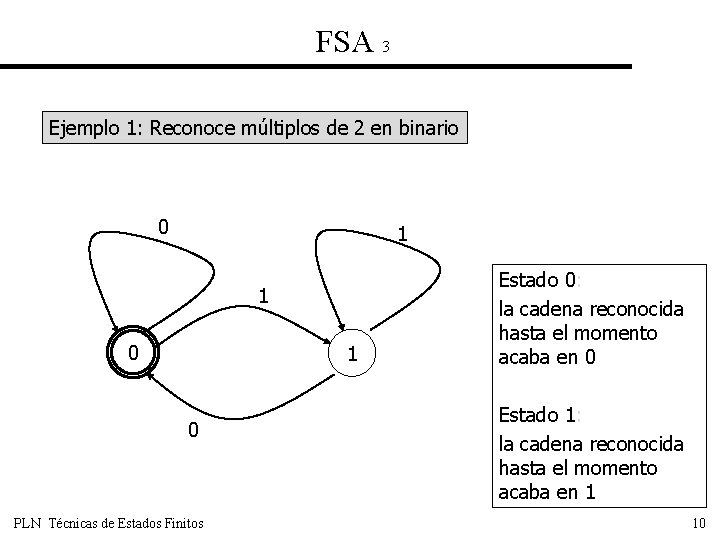
FSA 3 Ejemplo 1: Reconoce múltiplos de 2 en binario 0 1 1 0 PLN Técnicas de Estados Finitos Estado 0: la cadena reconocida hasta el momento acaba en 0 Estado 1: la cadena reconocida hasta el momento acaba en 1 10

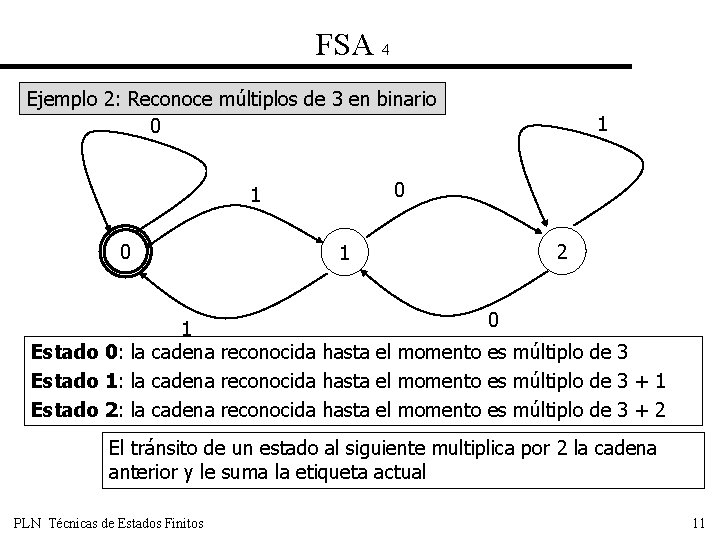
FSA 4 Ejemplo 2: Reconoce múltiplos de 3 en binario 0 0 1 1 2 0 1 Estado 0: la cadena reconocida hasta el momento es múltiplo de 3 Estado 1: la cadena reconocida hasta el momento es múltiplo de 3 + 1 Estado 2: la cadena reconocida hasta el momento es múltiplo de 3 + 2 El tránsito de un estado al siguiente multiplica por 2 la cadena anterior y le suma la etiqueta actual PLN Técnicas de Estados Finitos 11

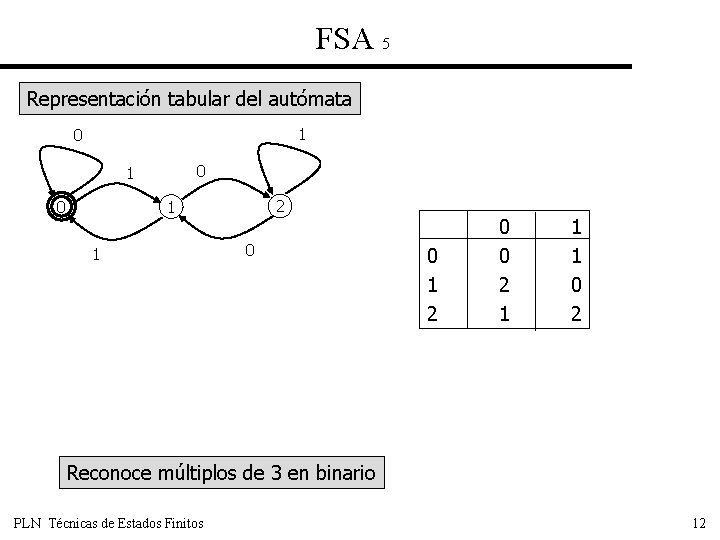
FSA 5 Representación tabular del autómata 1 0 0 1 0 2 1 1 0 0 1 2 0 0 2 1 1 1 0 2 Reconoce múltiplos de 3 en binario PLN Técnicas de Estados Finitos 12

FSA 6 • Propiedades de los RL y los FSA • Sea A un FSA • L(A) es el lenguaje generado (reconocido) por A • La clase de los RL (o FSA) es cerrada para • • • unión intersección concatenación complemento estrella de Kleene (A*) • Determinización de FSA • Minimización de FSA PLN Técnicas de Estados Finitos 13

FSA 7 • Las siguientes propiedades de los FSA son decidibles • w L(A) ? • L(A) = * ? • L(A 1) L(A 2) ? • L(A 1) = L(A 2) ? • Sólo las dos primeras lo son para CFG PLN Técnicas de Estados Finitos 14

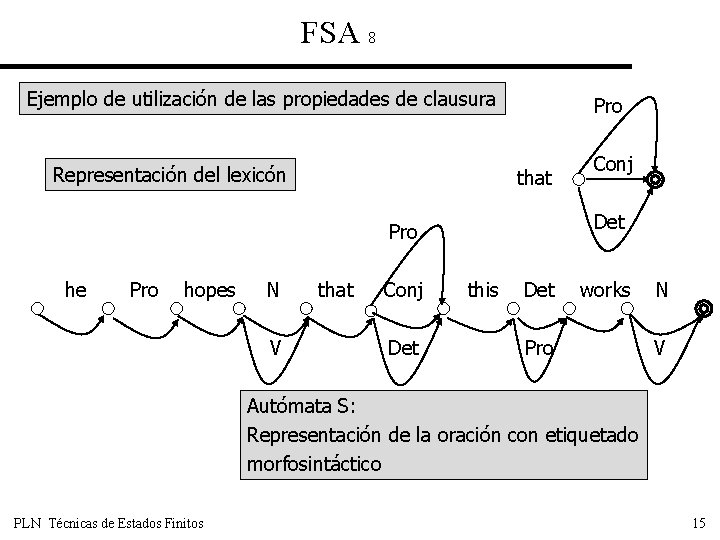
FSA 8 Ejemplo de utilización de las propiedades de clausura Representación del lexicón Pro that Det Pro he Pro hopes N V that Conj Det Conj this Det works Pro N V Autómata S: Representación de la oración con etiquetado morfosintáctico PLN Técnicas de Estados Finitos 15

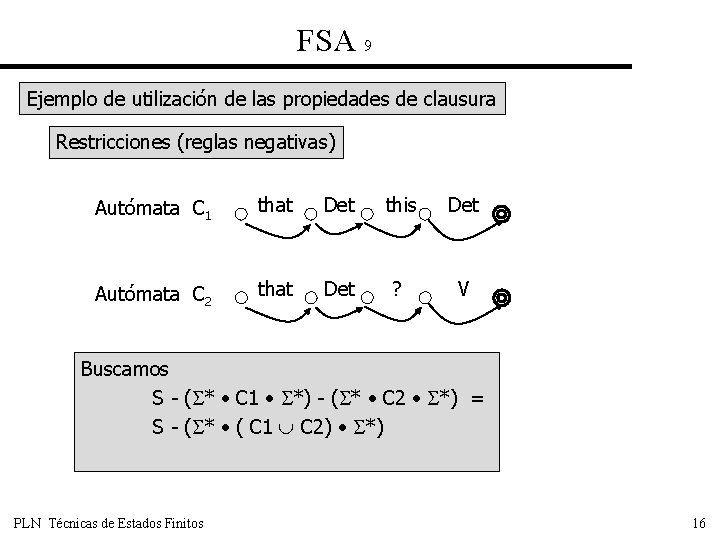
FSA 9 Ejemplo de utilización de las propiedades de clausura Restricciones (reglas negativas) Autómata C 1 that Det this Det Autómata C 2 that Det ? V Buscamos S - ( * • C 1 • *) - ( * • C 2 • *) = S - ( * • ( C 1 C 2) • *) PLN Técnicas de Estados Finitos 16

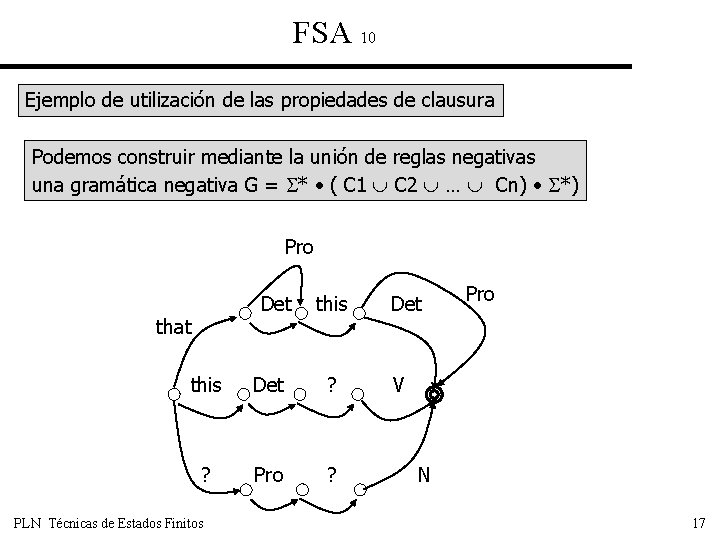
FSA 10 Ejemplo de utilización de las propiedades de clausura Podemos construir mediante la unión de reglas negativas una gramática negativa G = * • ( C 1 C 2 … Cn) • *) Pro Det that this Det ? ? Pro ? PLN Técnicas de Estados Finitos Det Pro V N 17

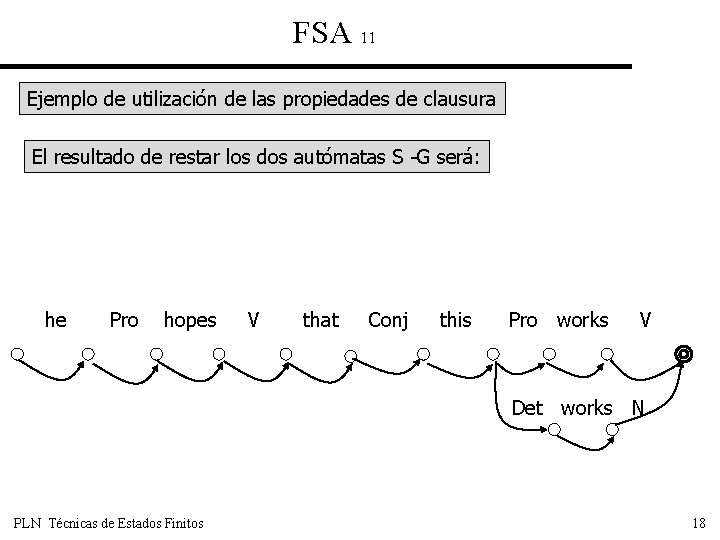
FSA 11 Ejemplo de utilización de las propiedades de clausura El resultado de restar los dos autómatas S -G será: he Pro hopes V that Conj this Pro works V Det works N PLN Técnicas de Estados Finitos 18

FST 1 • • • < 1, 2, Q, i, F, E> 1 2 alfabeto entrada alfabeto salida • a veces 1 = 2 = • • Q i Q F Q E Q ( 1* 2 *) Q PLN Técnicas de Estados Finitos conjunto finito de estados estado inicial conjunto de estados finales conjunto de arcos 19

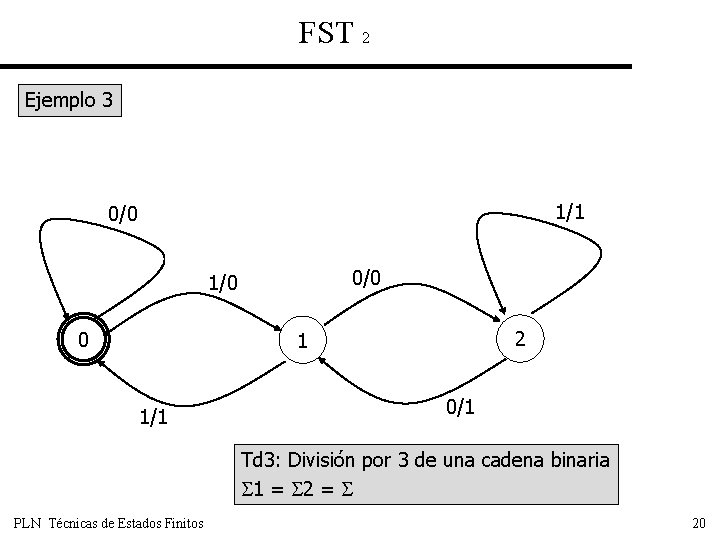
FST 2 Ejemplo 3 1/1 0/0 1/0 0 2 1 1/1 0/1 Td 3: División por 3 de una cadena binaria 1 = 2 = PLN Técnicas de Estados Finitos 20

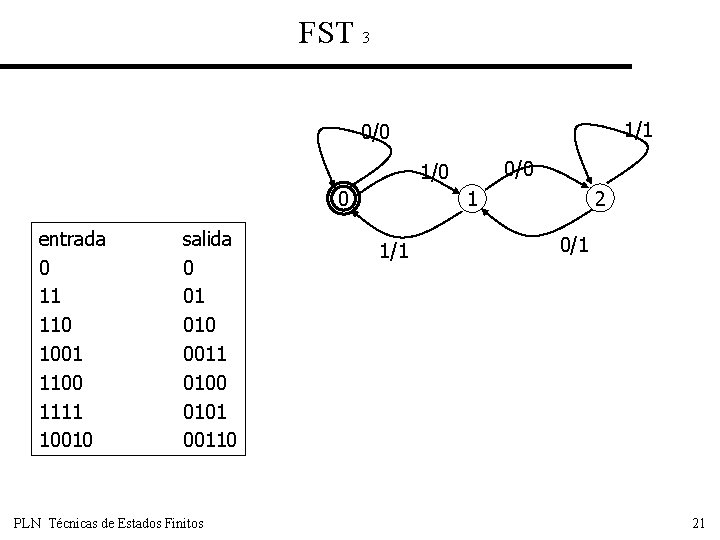
FST 3 1/1 0/0 1/0 0 entrada 0 11 110 1001 1100 1111 10010 salida 0 01 010 0011 0100 0101 00110 PLN Técnicas de Estados Finitos 2 1 1/1 0/1 21

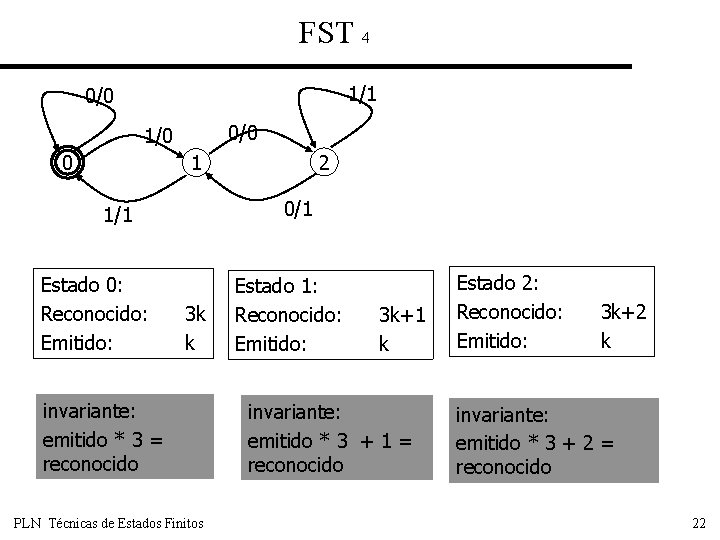
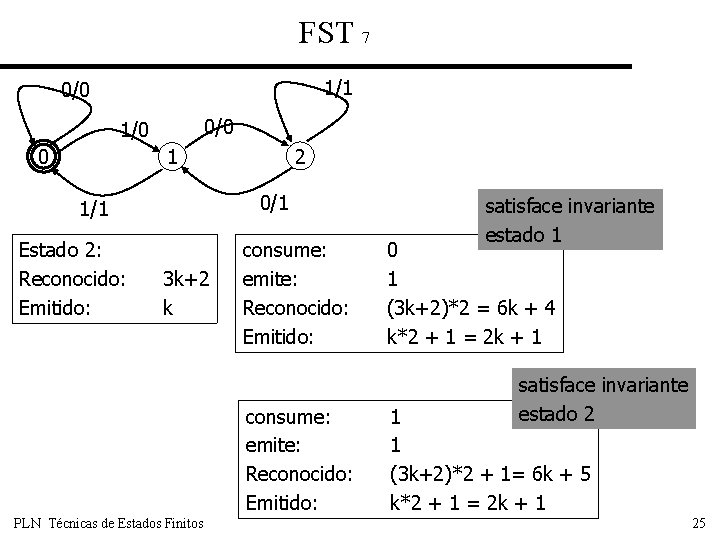
FST 4 1/1 0/0 1/0 0 2 1 0/1 1/1 Estado 0: Reconocido: Emitido: 3 k k invariante: emitido * 3 = reconocido PLN Técnicas de Estados Finitos Estado 1: Reconocido: Emitido: 3 k+1 k invariante: emitido * 3 + 1 = reconocido Estado 2: Reconocido: Emitido: 3 k+2 k invariante: emitido * 3 + 2 = reconocido 22

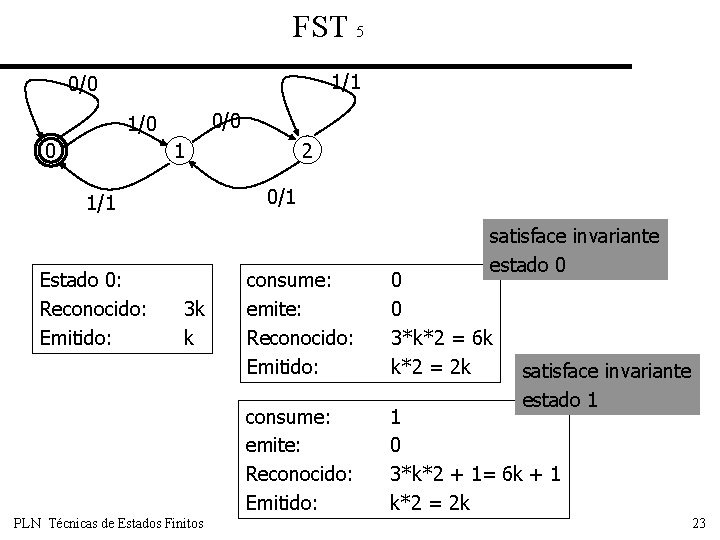
FST 5 1/1 0/0 1/0 0 2 1 0/1 1/1 Estado 0: Reconocido: Emitido: 3 k k PLN Técnicas de Estados Finitos satisface invariante estado 0 consume: emite: Reconocido: Emitido: 0 0 3*k*2 = 6 k k*2 = 2 k consume: emite: Reconocido: Emitido: 1 0 3*k*2 + 1= 6 k + 1 k*2 = 2 k satisface invariante estado 1 23

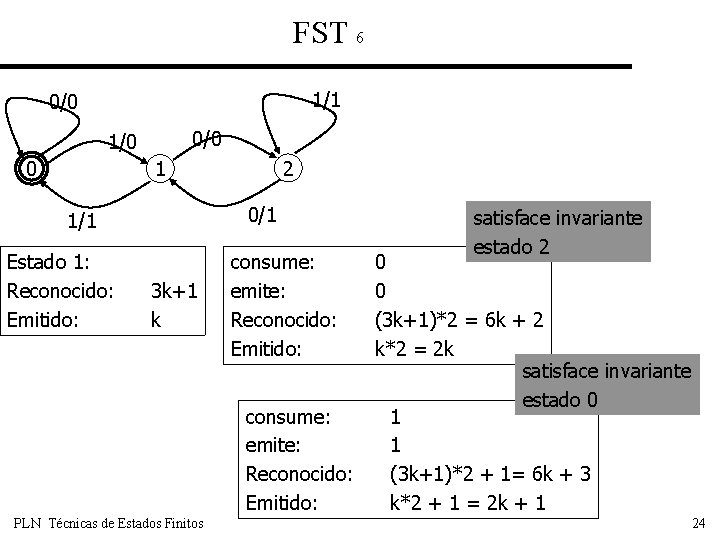
FST 6 1/1 0/0 1/0 0 2 1 0/1 1/1 Estado 1: Reconocido: Emitido: 3 k+1 k consume: emite: Reconocido: Emitido: PLN Técnicas de Estados Finitos satisface invariante estado 2 0 0 (3 k+1)*2 = 6 k + 2 k*2 = 2 k satisface invariante estado 0 1 1 (3 k+1)*2 + 1= 6 k + 3 k*2 + 1 = 2 k + 1 24

FST 7 1/1 0/0 1/0 0 2 1 0/1 1/1 Estado 2: Reconocido: Emitido: 3 k+2 k consume: emite: Reconocido: Emitido: PLN Técnicas de Estados Finitos satisface invariante estado 1 0 1 (3 k+2)*2 = 6 k + 4 k*2 + 1 = 2 k + 1 satisface invariante estado 2 1 1 (3 k+2)*2 + 1= 6 k + 5 k*2 + 1 = 2 k + 1 25

FST 8 FSA asociado a un FST • FST < 1, 2, Q, i, F, E> • FSA < , Q, i, F, E’> • = 1 2 • (q 1, (a, b), q 2) E’ (q 1, a, b, q 2) E PLN Técnicas de Estados Finitos 26

FST 9 Proyecciones de un FST T = < 1, 2, Q, i, F, E> • FST • primera proyección • P 1(T) < 1, Q, i, F, EP 1> • EP 1 = {(q, a, q’) | (q, a, b, q’) E} • segunda proyección • P 2(T) < 2, Q, i, F, EP 2> • EP 2 = {(q, b, q’) | (q, a, b, q’) E} PLN Técnicas de Estados Finitos 27

FST 10 • Los FST son cerrados para • unión • inversión • ejemplo: Td 3 -1 equivale a multiplicar por 3 • composición • ejemplo: Td 9 = Td 3 • Td 3 • Los FST no son cerrados para la intersección PLN Técnicas de Estados Finitos 28

FST 11 Aplicación de un FST • Recorrer el FST de todas las formas compatibles con la entrada (recurriendo al backtracking de ser necesario) hasta localizar un camino completo y obtener la salida correspondiente • Considerar que la entrada es un FSA y calcular la intersección del FSA con el FST PLN Técnicas de Estados Finitos 29

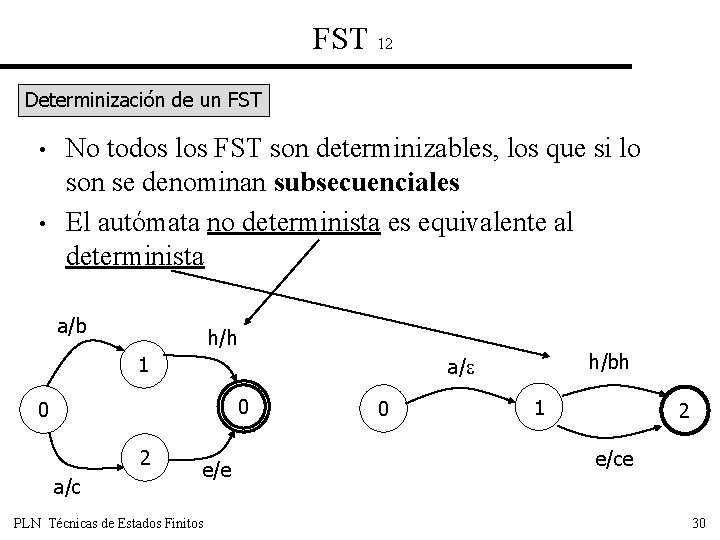
FST 12 Determinización de un FST • • No todos los FST son determinizables, los que si lo son se denominan subsecuenciales El autómata no determinista es equivalente al determinista a/b h/h 1 0 0 2 a/c h/bh a/ e/e PLN Técnicas de Estados Finitos 0 1 2 e/ce 30

FST en Xerox MLTT 1 [ab x] PLN Técnicas de Estados Finitos 31

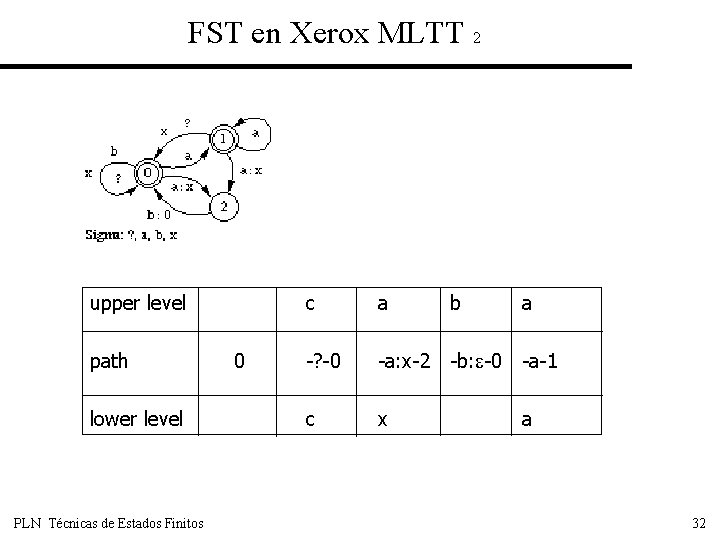
FST en Xerox MLTT 2 upper level path lower level PLN Técnicas de Estados Finitos 0 c a b a -? -0 -a: x-2 -b: -0 -a-1 c x a 32

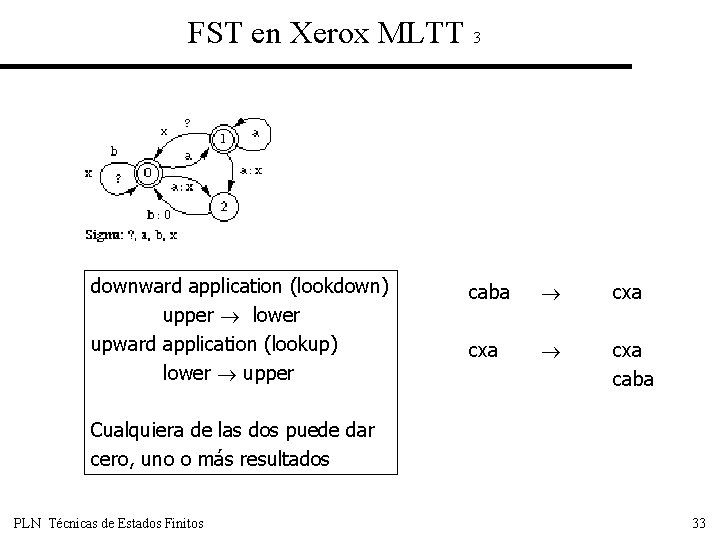
FST en Xerox MLTT 3 downward application (lookdown) upper lower upward application (lookup) lower upper caba cxa cxa caba Cualquiera de las dos puede dar cero, uno o más resultados PLN Técnicas de Estados Finitos 33